SAT Physics Subject Test
Chapter 7 Oscillations
THE KINEMATICS OF SHM
Now that we”ve explored the dynamics of the block”s oscillations in terms of force and energy, let”s talk about motion—kinematics. As you watch the block oscillate, you should notice that it repeats each cycle of oscillation in the same amount of time. A cycle is a round-trip: for example, from position x = A over to x = –A and back again to x = A. The amount of time it takes to complete a cycle is called the period of the oscillations, or T. If T is short, the block is oscillating rapidly, and if T is long, the block is oscillating slowly.
Another way of describing the rate of the oscillations is to count the number of cycles that can be completed in a given time interval; the more completed cycles, the faster the oscillations. The number of cycles that can be completed per unit time is called the frequency of the oscillations, orf, and frequency is expressed in cycles per second. One cycle per second is one hertz (abbreviated Hz).
One of the most basic equations of oscillatory motion is
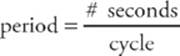while 
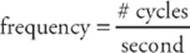
Therefore
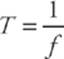and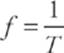 
4. A block oscillating on the end of a spring moves from its position of maximum spring stretch to maximum spring compression in 0.25 s. Determine the period and frequency of this motion.
Here”s How to Crack It
The period is defined as the time required for one full cycle. Moving from one end of the oscillation region to the other is only half a cycle. Therefore, if the block moves from its position of maximum spring stretch to maximum spring compression in 0.25 s, the time required for a full cycle is twice as much; T = 0.5 s. Because frequency is the reciprocal of period, the frequency of the oscillations is f = 1/T = 1/(0.5 s) = 2 Hz.
5. A student observing an oscillating block counts 45 cycles of oscillation in one minute. Determine its frequency (in hertz) and period (in seconds).
Here”s How to Crack It
The frequency of the oscillations, in hertz (which is the number of cycles per second), is
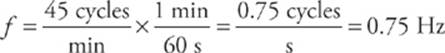
Therefore
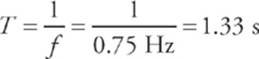
One of the defining properties of the spring–block oscillator is that the frequency and period can be determined from the mass of the block and the force constant of the spring. The equations are as follows:
Let”s analyze these equations. Suppose we had a small mass on a very stiff spring; then we would expect that this strong spring would make the small mass oscillate rapidly, with high frequency and short period. Both of these predictions are proved true by the equations above because if m is small and k is large, then the ratio k/m is large (high frequency) and the ratio m/k is small (short period).
6. How would the period of the spring–block oscillator change if both the mass of the block and the spring constant were doubled?
Here”s How to Crack It
The equation given above for the period shows that T depends on m/k. If both m and k are doubled, then the ratio m/k will be unchanged. Therefore, T will be unchanged too.
7. A block is attached to a spring and set into oscillatory motion, and its frequency is measured. If this block were removed and replaced by a second block with 1/4 the mass of the first block, how would the frequency of the oscillations compare to that of the first block?
Here”s How to Crack It
Since the same spring is used, k remains the same. According to the equation given above, f is inversely proportional to the square root of the mass of the block: f ∞ 1/
. Therefore, if m decreases by a factor of 4, then f increases by a factor of 
= 2.
The equations we saw above for the frequency and period of the spring–block oscillator do not contain A, the amplitude of the motion.
In simple harmonic motion, both the frequency and the period are independent of the amplitude.
8. A student performs an experiment with a spring–block simple harmonic oscillator. In the first trial, the amplitude of the oscillations is 3.0 cm, while in the second trial (using the same spring and block), the amplitude of the oscillations is 6.0 cm. Compare the values of the period, frequency, and maximum speed of the block between these two trials.
Here”s How to Crack It
If the system exhibits simple harmonic motion, then the period and frequency are independent of amplitude. This is because the same spring and block were used in the two trials, so the period and frequency will have the same values in the second trial as they had in the first. But the maximum speed of the block will be greater in the second trial than in the first. Since the amplitude is greater in the second trial, the system possesses more total energy (E = 
kA2). So when the block is passing through equilibrium (its position of greatest speed), the second system has more energy to convert to kinetic, meaning that the block will have a greater speed. In fact, from question 2 we know that vmax = 
, so since A is twice as great in the second trial than in the first, vmax will be twice as great in the second trial than in the first.
For undergoing simple harmonic motion, the position x can be expressed as a sine or cosine function in terms of t.
x = A cos(2πft + Ø) or x = A sin(2πft +Ø)
Ø is called the phase, and is determined by the initial conditions. For example, if x = A at t = 0, then choosing the cosine version of the equation would mean ¸ = 0 = 0. (Remember that cos0=1). x = A cos(2πft).
9. For each of the following arrangements of two springs, determine the effective spring constant, keff. This is the force constant of a single spring that would produce the same force on the block as the pair of springs shown in each case.
(a)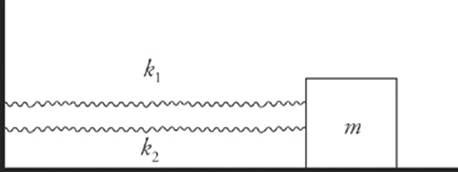 
(b)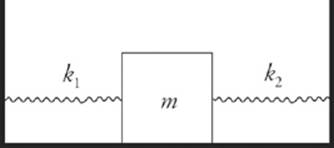 
(c)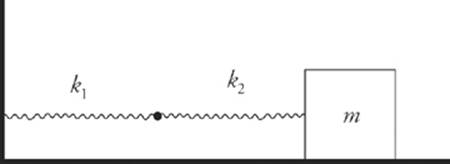 
(d) Determine keff in each of these cases if k1 = k2 = k.
Here”s How to Crack It
(a) Imagine that the block was displaced a distance x to the right of its equilibrium position. Then the force exerted by the first spring would be F1 = –k1x and the force exerted by the second spring would be F2 = –k2x. The net force exerted by the springs would be
F1 + F2 = –k1x + –k2x = –(k1 + k2)x
Since Feff = –(k1 + k2)x, we see that keff = k1 + k2.
(b) Imagine that the block was displaced a distance x to the right of its equilibrium position. Then the force exerted by the first spring would be F1 = –k1x and the force exerted by the second spring would be F2 = –k2x. The net force exerted by the springs would be
F1 + F2 = –k1x + –k2x = –(k1 + k2)x
As in part (a), we see that, since Feff = –(k1 + k2)x, we get keff = k1 + k2.
(c) Imagine that the block was displaced a distance x to the right of its equilibrium position. Let x1 be the distance that the first spring is stretched, and let x2 be the distance that the second spring is stretched. Then x = x1 + x2. But x1 = –F/k1 and x2 = –F/k2, so
Therefore
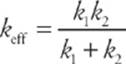
(d) If the two springs have the same force constant, that is, if k1 = k2 = k, then in the first two cases, the pairs of springs are equivalent to one spring that has twice their force constant: keff = k1 + k2 = k + k = 2k. In (c), the pair of springs is equivalent to a single spring with half their force constant.
keff = 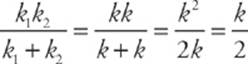