SAT Physics Subject Test
Chapter 9 Electric Potential and Capacitance
COMBINATIONS OF CAPACITORS
When a capacitor charges up, work must be done by an external force (for example a battery). This increases the potential energy stored by the capacitor. The potential energy stored is given by the formula
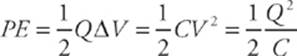
Capacitors are often arranged in combination in electric circuits. Let”s review two types of arrangements: the parallel combination and the series combination.
A collection of capacitors are said to be in parallel if they all share the same potential difference. The following diagram shows two capacitors wired in parallel.
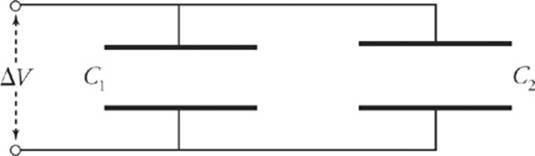
The top plates are connected by a wire and form a single equipotential; the same is true for the bottom plates. Therefore, the potential difference across one capacitor is the same as the potential difference across the other capacitor.
If we want to find the capacitance of a single capacitor that would perform the same function as this combination, and if the capacitances are C1 and C2, then the charge on the first capacitor is Q1 = C1ΔV and the charge on the second capacitor is Q2 = C2ΔV. The total charge on the combination is Q1 + Q2 , so the equivalent capacitance, CP, must be
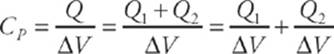
so
Cp = C1 + C2
which can be extended to more than 2 capacitors. So the equivalent capacitance of a collection of capacitors in parallel is found by adding the individual capacitances.
A collection of capacitors are said to be in series if they all share the same charge magnitude. The following diagram shows two capacitors wired in series.
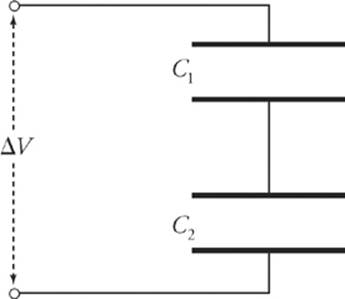
When a potential difference is applied, as shown, negative charge will be deposited on the bottom plate of the bottom capacitor; this will push an equal amount of negative charge away from the top plate of the bottom capacitor toward the bottom plate of the top capacitor. When the system has reached equilibrium, the charges on all the plates will have the same magnitude.
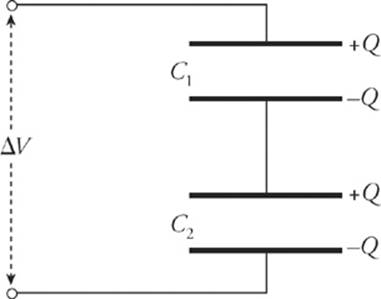
If the top and bottom capacitors have capacitances of C1 and C2, respectively, then the potential difference across the top capacitor is ΔV1 = Q/C1, and the potential difference across the bottom capacitor is ΔV2 = Q/C2. The total potential difference across the combination is Δ V1 + Δ V2, which equals Δ V. Therefore, the equivalent capacitance, CS, must be
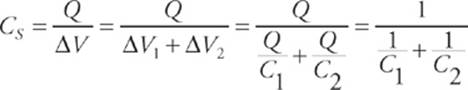
This can be written as
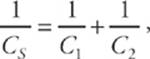
which can also be extended to more than 2 capacitators. As you can see, the reciprocal of the capacitance of a collection of capacitors in series is found by adding the reciprocals of the individual capacitances.
![]()
![]()
8. Given that C1 = 2 µF, C2 = 4 µF, and C3 = 6 µF, calculate the equivalent capacitance for the following combination:
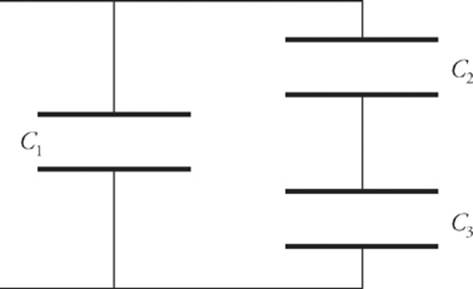
Here”s How to Crack It
Notice that C2 and C3 are in series, and they are in parallel with C1. That is, the capacitor equivalent to the series combination of C2 and C3 (which we”ll call C2–3) is in parallel with C1. We can represent this as follows:
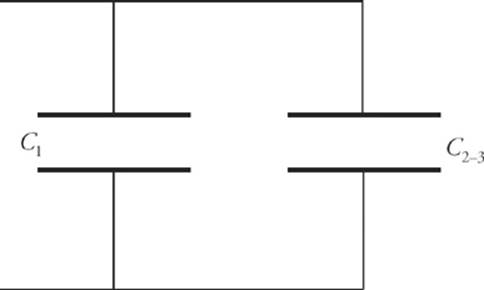
So the first step is to find C2–3.
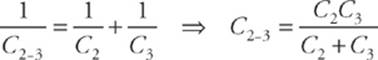
Now this is in parallel with C1, so the overall equivalent capacitance (C1–2–3) is
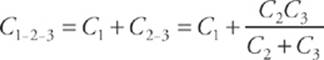
Substituting in the given numerical values, we get
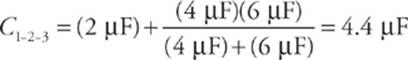
![]()