SAT Test Prep
CHAPTER 8
ESSENTIAL ALGEBRA I SKILLS
Lesson 7: Word Problems
How to Attack Word Problems
Don”t be afraid of word problems—they”re easier than they look. In word problems, the facts about the unknowns are written as sentences instead of equations. So all you have to do is name the unknowns and translate the sentences into equations. Then it”s all algebra.
Step 1: Read the problem carefully, and try to get “the big picture.” Note carefully what the question asks you to find.
Step 2: Ask: what are the unknowns? Call them x or n or some other convenient letter. Don”t go overboard. The fewer the unknowns, the simpler the problem. For instance, if the problem says, “Dave weighs twice as much as Eric,” rather than saying ![]() (which uses two unknowns), it might be simpler to say that Eric weighs x pounds and Dave weighs 2x pounds (which only uses one unknown).
(which uses two unknowns), it might be simpler to say that Eric weighs x pounds and Dave weighs 2x pounds (which only uses one unknown).
Step 3: Translate any key sentence in the question into an equation. If your goal is to solve for each unknown, you”ll need the same number of equations as you have unknowns. Use this handy translation key to translate sentences into equations:

Step 4: Solve the equation or system. Check the question to make sure that you”re solving for the right thing. Review Lessons 1 and 2 in this chapter if you need tips for solving equations and systems.
Step 5: Check that your solution makes sense in the context of the problem.
Example:
Ellen is twice as old as Julia. Five years ago, Ellen was three times as old as Julia. How old is Julia now?
Let”s say that this is a grid-in question, so you can”t just test the choices. Guessing and checking might work, but it also may take a while before you guess the right answer. Algebra is quicker and more reliable. First, think about the unknowns. The one you really care about is Julia”s currentage, so let”s call it j. We don”t know Ellen”s current age either, so let”s call it e. That”s two unknowns, so we”ll need two equations. The first sentence, Ellen is twice as old as Julia, can be translated as ![]() . The next sentence, Five years ago, Ellen was three times as old as Julia, is a bit trickier to translate. Five years ago, Ellen was
. The next sentence, Five years ago, Ellen was three times as old as Julia, is a bit trickier to translate. Five years ago, Ellen was ![]() years old, and Julia was
years old, and Julia was ![]() years old. So the statement translates into
years old. So the statement translates into ![]() . Now solve the system:
. Now solve the system:
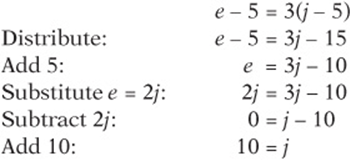
Now reread the problem and make sure that the answer makes sense. If Julia is 10, Ellen must be 20 because she”s twice as old. Five years ago, they were 5 and 15, and 15 is three times 5! It works!
Concept Review 7: Word Problems
For each of the following statements, specify and name the unknowns and translate the statement into an equation.
1. Mike is twice as old as Dave was 5 years ago.
2. The population of town A is 40% greater than the population of town B.
3. After 2/3 of the marbles are removed from a jar, 5 more than 1/6 of the marbles remain.
4. In a jar, there are 4 more than twice as many blue marbles as red marbles.
Solve the following word problems.
5. Three candy bars and two lollipops cost $2.20, and four candy bars and two lollipops cost $2.80. What is the cost of one lollipop?
6. At a football stadium, 2/3 of the seats were filled at the beginning of a game. At halftime, 1,000 people left the stadium, leaving 3/7 of the seats filled. What is the total number of seats in the stadium?
7. If the average of m and n is one-half of the average of s and t, then what is s in terms of m, n, and t?
8. A blue chip is worth 2 dollars more than a red chip, and a red chip is worth 2 dollars more than a green chip. If 5 green chips are worth m dollars, give an expression that represents the price, in dollars, of 10 blue chips and 5 red chips.
SAT Practice 7: Word Problems
1. When x is subtracted from 24 and this difference is divided by x, the result is 3. What is x?
(A) 4
(B) 5
(C) 6
(D) 8
(E) 12
2. Three years ago, Nora was half as old as Mary is now. If Mary is four years older than Nora, how old is Mary now?

3. If the ratio of p to q is 9:7 and the ratio of q to r is 14:3, then what is the ratio of p to r?
(A) 1:6
(B) 27:98
(C) 2:5
(D) 5:2
(E) 6:1
4. Joan originally had twice as many books as Emily. After she gave Emily 5 books, Joan still had 10 more than Emily. How many books did Joan have originally?

5. The cost of living in a certain city rose 20% between 1960 and 1970, and rose 50% between 1960 and 1980. By what percent did the cost of living increase between 1970 and 1980?
(A) 15%
(B) 20%
(C) 25%
(D) 30%
(E) 35%
6. The Mavericks baseball team has a won-lost ratio of 7 to 5. If the team played a total of 48 games and no game ended in a tie, how many more games have the Mavericks won than they have lost?

7. When the Apex Pet Store first opened, the ratio of cats to dogs was 4 to 5. Since then, the number of cats has doubled, while the number of dogs has increased by 12. If the ratio of dogs to cats is now 1 to 1, how many cats did the store have when it opened?

8. Hillside High School has 504 students. One-quarter of the students are sophomores, and 3/7 of the sophomores are boys. If one-third of the sophomore girls take French, how many sophomore girls do not take French?
(A) 24
(B) 36
(C) 48
(D) 72
(E) 126
9. A jar contains only red, green, and blue marbles. If it is three times as likely that you randomly pick a red marble as a green marble, and five times as likely that you pick a green one as a blue one, which of the following could be the number of marbles in the jar?
(A) 38
(B) 39
(C) 40
(D) 41
(E) 42
Answer Key 7: Word Problems
Concept Review 7
1. m = Mike”s current age, d = Dave”s current age; ![]()
2. a = the population of town A, b = the population of town B; ![]()
3. n = number of marbles in the jar; ![]()
4. b = number of blue marbles, r = number of red marbles; ![]()
5. c = cost of one candy bar, l = cost of one lollipop; ![]() , and
, and ![]() .
.
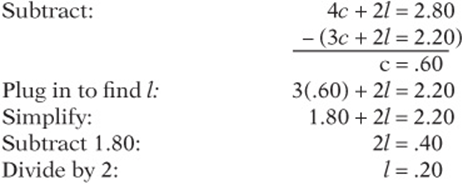
6. n number of seats in the stadium;
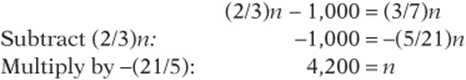
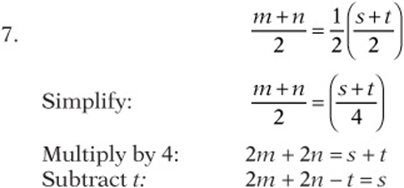
8. b value of blue chip, r = value of red chip, g = value of green chip; ![]() ,
, ![]() , and
, and ![]() , so
, so
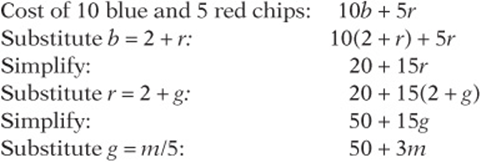
SAT Practice 7
1. C You could test the choices here, or do the

2. n = Nora”s current age, m = Mary”s current age.
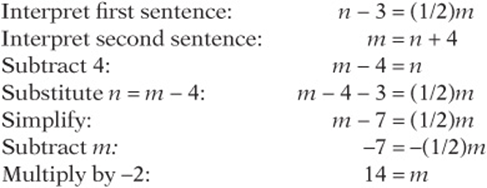
3. E ![]() ,
,![]() .
.
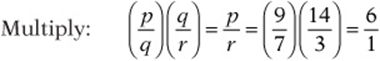
4. 40 J number of books Joan had originally. E = number of books Emily had originally. ![]() . After the exchange, Emily has E + 5 and joan has j – 5 book, so
. After the exchange, Emily has E + 5 and joan has j – 5 book, so ![]() .
.
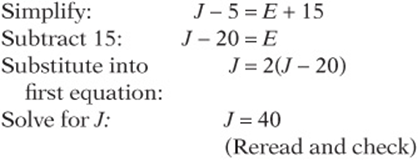
5. C Let x be the cost of living in 1960. In 1970, the cost of living was 1.2x, and in 1980 it was 1.5x. Use the percent change formula: ![]() .
.
6. 8 Let w = the number of games won and l = the number of games lost. ![]() and
and ![]() .
.

7. 16 Let c = number of cats originally, d = number of dogs originally. ![]() . Now the number of cats is 2c and the number of dogs is
. Now the number of cats is 2c and the number of dogs is ![]() . If the ratio of dogs to cats is now 1 to 1,
. If the ratio of dogs to cats is now 1 to 1, ![]() .
.
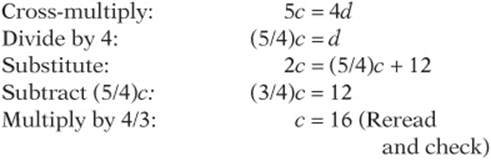
8. C Number of sophomores ![]() . If 3/7 of the sophomores are boys, 4/7 are girls:
. If 3/7 of the sophomores are boys, 4/7 are girls: ![]() . If 1/3 of the sophomore girls take French, 2/3 do not:
. If 1/3 of the sophomore girls take French, 2/3 do not: ![]() .
.
9. E r, g, and b are the numbers of red, green, and blue marbles. ![]() and
and ![]() . Total marbles
. Total marbles ![]() .
.

So the total must be a multiple of 21, and ![]() .
.