SAT 2016
CHAPTER 7
THE SAT MATH TEST: THE HEART OF ALGEBRA
Skill 3: Working with Inequalities and Absolute Values
Lesson 8: Understanding inequalities and absolute values
On the real number line, a number, b, is more than twice as far from −3 as it is from 3. Which of the following equations can be solved to find all possible values of b?
A) |b − 3| > 2|b + 3|
B) |b + 3| > 2|b − 3|
C) 2|b − 3| > |b + 3|
D) 2|b + 3| > |b − 3|
Distance and absolute value
The absolute value of a number x, written as |x|, means its distance from 0 on the number line. In fact, we can use absolute value to represent the distance between any two numbers.
|x − a| means the distance between x and a on the number line.
Notice that this works no matter which number is greater. For instance, the distance between 2 and 7 is |2 − 7| = |−5| = 5, which is the same as the distance between 7 and 2: |7 − 2| = |5| = 5.
Notice that an expression like |x + a| is equivalent to |x − (−a)|, which means that |x + a| can be translated as the distance between x and −a.
(Medium-hard) We can use this definition to translate the problem. The key is to translate the statement “b is more than twice as far from −3 as it is from 3” into a statement about distances: “The distance between b and −3 is more than twice the distance between b and 3.” Notice how easily this translates into an inequality:
(The distance between b and −3) is more than (twice the distance between b and 3)
|b − (−3)| > 2|b − 3|
|b + 3| > 2|b − 3|
which is choice (B).
Lesson 9: Solving inequalities with the Laws of Inequality
If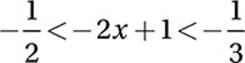 
, what is one possible value of x?
(Easy) This kind of inequality is called a “sandwich inequality” because the expression in the middle is between the other two, like meat between slices of bread. Working with inequalities like this one requires understanding the Laws of Inequality.
The Laws of Inequality
Every inequality is a “tipped” scale, and the Laws of Inequality are simply the rules for “keeping the scale tipped the right way,” that is, deducing other true inequalities that follow from the original one. In a nutshell, the Laws of Inequality say that
1. You may make changes to any inequality, as long as you follow rules 2, 3 and 4.
2. Whatever you do to one side of the inequality, you must do to the other.
3. You may not perform undefined operations (like dividing by 0), or operations that have more than one possible result (like taking a square root).
4. If you multiply or divide both sides by a negative number, you must “switch” the direction of the inequality. This is because multiplying or dividing by a negative number involves a reflection over the origin on the number line, and this reflection requires the “switch”:
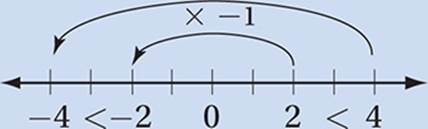
So we can solve the sandwich inequality by applying the correct laws of inequality:
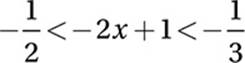
Multiply by −6 (the common denominator) and “switch:”
3 > 12x − 6 > 2
Add 6:
9 > 12x > 8
Divide by 12:
0.75 > x > 0.66 …
Therefore, any value greater than 0.666 but less than 0.750 is correct.
Which of the following must be true if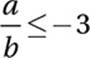 
?
A) a ≤ −3b
B) a ≥ −3b
C) a ≤ −3b < 0 or a ≥ −3b > 0
D) a ≤ −3b < 0 or a ≥ −3b > 0
(Hard) We might be tempted to multiply both sides of the inequality by b and get the inequality in (A). But this would be incorrect because it would ignore rule 4. We need to consider the possibility that b might be negative. Let”s think about possible solutions to the original inequality. Notice that a = 10 and b = −2 gives a possible solution, because 10/(−2) = −5 ≤ −3. But this would not satisfy the inequality in (A): 10 is not less than or equal to (−3)(−2) = 6.
To solve this inequality, we will need to consider two distinct possible conditions:
Condition 1: If b > 0, then a ≤ −3b and therefore a ≤ −3b < 0
Condition 2: If b < 0, then a ≥ −3b and therefore a ≥ −3b > 0
which is the answer in choice (D).
Lesson 10: Graphing inequalities
On the real number line, a number, b, is more than twice as far from −3 as it is from 3. Which of the following graphs represents all possible values of b?
A)
B)
C)
D)
(Medium) We saw this scenario in Lesson 8, but now we are asked to graph the solution. Recall from Lesson 8 that this relationship is expressed by the inequality |b + 3| > 2|b − 3|. How do we translate this into a graph? The simplest way to start is to visualize the number line, and to think about a related, but simpler, question: What if b is exactly twice as far from −3 as it is from 3? A little guessing and checking should reveal that two points work:
Notice that 9 works because 3 is the midpoint between −3 and 9, and 1 works because it is 2/3 of the way from −3 to 3. Also, you can confirm that both numbers satisfy the equation |b + 3| = 2|b − 3|. These two points now divide the line into three parts: everything less than 1, everything between 1 and 9, and everything greater than 9. A little bit of checking (just pick a number from each portion and plug it into our inequality) confirms that only the numbers in the middle portion satisfy our inequality, so the correct graph is the one in choice (D).
When graphing inequalities, it often helps to start with the graph of the corresponding equation and work from there. The graph of the equation usually provides the boundaries for the graph of the inequality.
Exercise Set 4 (No Calculator)
1
What positive number is twice as far from 10 as it is from 1?
2
If the points (2, a) and (14, b) are 20 units apart, what is |a − b|?
3
What is the least integer n for which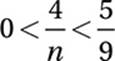 
?
4
If |x + 4| = |x − 5|, what is the value of x?
5
What is the greatest integer value of n such that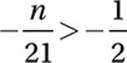 
?
6
What is the only integer b for which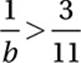 
and 3b ≥ 7.5?
7
If (b + 2)2 = (b − 5)2, what is the value of b?
8
Which of the following statements is equivalent to the statement −4 < 2x ≤ 2?
A) x > −2 and x ≤ 1
B) x < −2 or x ≥ 1
C) x ≥ −2 and x < 1
D) x ≤ −2 or x > 1
9
The annual profit from the sales of an item is equal to the annual revenue minus the annual cost for that item. The revenue from that item is equal to the number of units sold times the price per unit. If n units of a portable heart monitor were sold in 2012 at a price of $65 each, and the annual cost to produce n units was $(20,000 + 10n), then which of the following statements indicates that the total profit for this heart monitor in 2012 was greater than $500,000?
A) 500,000 < 55n − 20,000
B) 500,000 > 55n − 20,000
C) 500,000 < 55n + 20,000n
D) 500,000 < 75n − 20,000n
10
Colin can read a maximum of 25 pages an hour. If he has been reading a 250 page book for h hours, where h < 10, and has p pages left to read, which of the following expresses the relationship between p and h?
A)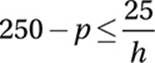 
B)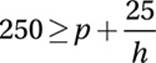 
C) 250 − p ≤ 25h
D) 250 + 25h ≤ p
11
On the real number line, a number, x, is more than 4 times as far from 10 as it is from 40. Which of the following statements describes all possible values of x?
A) x < 34 or x > 50
B) x > 40
C) 34 < x < 50
D) 32.5 < x < 160
Exercise Set 4 (Calculator)
12
If a < 0 and |a − 5| = 7, what is |a|?
13
If n is a positive integer and 16 > |6 − 3n| > 19, what is the value of n?
14
What is the only integer n such that 20 − 2n > 5 and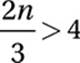 
?
15
What is the smallest number that is as far from 9.25 as 3 is from −1.5?
16
If |2x + 1| = 2|k − x|, for all values of x, what is the value of |k|?
17
Which of the following is equivalent to the statement |x − 2| < 1?
A) x < 3
B) x < −1
C) 1 < x < 3
D) −1 < x < 3
18
If the average (arithmetic mean) of a and b is greater than the average (arithmetic mean) of c and 2b, which of the following must be true?
A) b > 0
B) a > b
C) a > b + c
D) a + c > b
19
Of the statements below, which is equivalent to the statement “The distance from x to 1 is greater than the distance from x to 3?
A) 1 < x < 3
B) x > 2
C) x < 2
D) x − 1 > 3
20
Which of the following is equivalent to the statement 4x2 ≥ 9?
A) 2x > 3
B) x ≥ 1.5 or x ≤ −1.5
C) |x| > 2
D) −1.5 ≤ x ≤ 1.5
21
The graph above indicates the complete solution set to which of the following statements?
A) |x − 3| > 3
B) |x| < 6
C) |x − 6| < 6
D) |x − 3| < 3
22
Which of the following is true for all real values of x?
A) |x| > 0
B) x < 2 or x > 1
C) x > −2 or x < −3
D) x2 − 1 > 0
EXERCISE SET 4 ANSWER KEY
No Calculator
1. 4 It is helpful to plot these values on the number line and think:
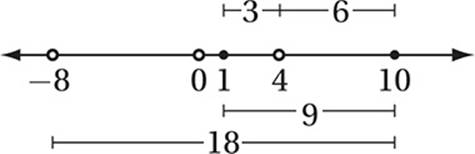
The distance between 1 and 10 is 9, so clearly the number that is 9 more units to the left of 1, namely −8, is twice as far from 10 as it is from 1. However, this is a negative number so it can”t be our answer. There is one other number that is twice as far from 10 as it is from 1: the number that is 1/3 the distance from 1 to 10. This number is 4, which is 3 units from 1 and 6 units from 10.
2. 16 From the Distance Formula,
(2 − 14)2 + (a − b)2 = 202
Simplify:
144 + (a − b)2 = 400
Subtract 144:
(a − b)2 = 256
Square root:
|a − b| = 16
3. 8
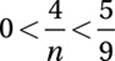
Since n must be positive for this statement to be true, we can multiply by 9n without having to “swap” the inequality symbols:
0 < 36 < 5n
Divide by 5:
0 < 7.2 < n
Therefore, the smallest integer value of n is 8.
4. ½ or .5 Two numbers, a and b, have the same absolute value only if they are equal or opposites. Clearly x + 4 and x − 5 cannot be equal, since x − 5 is 9 less than x + 4. Therefore they must be opposites.
x + 4 = −(x − 5)
Distribute:
x + 4 = −x + 5
Add x:
2x + 4 = 5
Subtract 4:
2x = 1
Divide by 2:
x = 1/2
5. 10
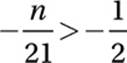
Multiply by −42 and “swap:”
2n < 21
Divide by 2:
n < 10.5
Therefore, the greatest possible integer value of n is 10.
6. 3
3b ≥ 7.5
Divide by 3:
b ≥ 2.5
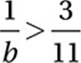
Since b is greater than or equal to 2.5, it is positive, so we can multiply both sides by 11b without “swapping” the inequality:
11 > 3b
Divide by 3:
3.67 > b
The only integer between 2.5 and 3.67 is 3.
7. 3/2 or 1.5
(b + 2)2 = (b − 5)2
FOIL:
b2 + 4b + 4 = b2 − 10b + 25
Subtract b2:
4b + 4 = −10b + 25
Add 10b:
14b + 4 = 25
Subtract 4:
14b = 21
Divide by 14:
b = 1.5
8. A
−4 < 2x ≤ 2
Divide by 2:
−2 < x ≤ 1
which is equivalent to −2 < x and x ≤ 1.
9. A The profit is the revenue minus the cost: 65n − (20,000 + 10n) = 55n − 20,000.
10. C If Colin can read a maximum of 25 pages an hour, then in h hours he can read a maximum of 25h pages. If he has p pages left in a 250-page book, he has read 250 − p pages. Since it has taken him h hours to read these 250 − p pages, 250 − p ≤ 25h.
11. C
|x − 10| > 4|x − 40|
It helps to sketch the number line and divide is into three sections: the numbers less than 10, the numbers between 10 and 40, and the numbers greater than 40.
CASE 1: x < 10. It should be clear that all numbers less than 10 are closer to 10 than they are to 40, so this set contains no solutions.
CASE 2: 10 < x ≤ 40. If x is between 10 and 40, x − 10 is positive and x − 40 is negative, so |x − 10| = x − 10 and |x − 40| = −(x − 40).
|x − 10| > 4|x − 40|
Substitute:
x − 10 > −4(x − 40)
Distribute:
x − 10 > −4x + 160
Add 4x:
5x − 10 > 160
Add 10:
5x > 170
Divide by 5:
x > 34
So this gives us 34 < x ≤ 40.
CASE 3: x > 40. If x is greater than 40, then both x − 10 and x − 40 are positive, so |x − 10| = x − 10 and |x − 40| = x − 40.
|x − 10| > 4|x − 40|
Substitute:
x − 10 > 4(x − 40)
Distribute:
x − 10 > 4x − 160
Add 10:
x > 4x − 150
Subtract 4x:
−3x > −150
Divide by −3 and “swap:”
x < 50
So this gives us 40 < x < 50. When we combine this with the solutions from CASE 2, we get 34 < x < 50.
Calculator
12. 2 If |a − 5| = 7, then either a − 5 = 7 or a − 5 = − 7, so either a = 12 or a = −2. Since a < 0, a must be −2, and |−2| = 2.
13. 8 CASE 1: If 6 − 3n is positive, then
|6 − 3n| = 6 − 3n, so
16 > 6 − 3n > 19
Subtract 6:
10 > −3n > 13
Divide by −3 and “swap:”
−10/3 < n < −13/3
But this contradicts the fact that n is positive.
CASE 2: If 6 − 3n is negative, then
|6 − 3n| = −(6 − 3n), so
16 > −(6 − 3n) > 19
Distribute:
16 > −6 + 3n > 19
Add 6:
22 > 3n > 25
Divide by 3:
7.33 > n > 8.33
And the only integer in this range is n = 8.
14. 7
20 − 2n > 5
Subtract 20:
−2n > −15
Divide by −2 and “swap:”
n < 7.5
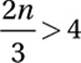
Multiply by 3:
2n > 12
Divide by 2:
n > 6
Since n must be an integer between 6 and 7.5, n = 7.
15. 4.75 The distance from 3 to −1.5 is |3−(−1.5)| = 4.5. Therefore the two numbers that are 4.5 away from 9.25 are 9.25 + 4.5 = 13.75 and 9.25 − 4.5 = 4.75.
16. ½ or .5 If the equation is true for all values of x, let”s choose a convenient value for x,
like x = 1.
|2x + 1| = 2|k − x|
Substitute x = 1:
|2(1) + 1| = 2|k − 1|
Simplify:
3 = 2|k − 1|
Divide by 2:
1.5 = |k − 1|
Therefore
±1.5 = k − 1
Add 1:
k = 2.5 or −0.5
Now try x = 0:
|2(0) + 1| = 2|k − 0|
Simplify:
1 = 2|k|
Divide by 2:
0.5 = |k|
Therefore
±0.5 = k
Therefore, k = −0.5 and so |k| = |−0.5| = 0.5.
17. C Recall that the expression |x − 2| means “the distance from x to 2,” so the statement |x − 2| < 1 means “The distance from x to 2 is less than 1.” Therefore, the solution set is all of the numbers that are less than 1 unit away from 2, which are all the numbers between 1 and 3.
18. C
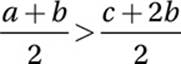
Multiply by 2:
a + b > c + 2b
Subtract b:
a > c + b
19. B The formal translation of this statement is |x − 1| > |x − 3|, which we can solve algebraically by considering three cases: (I) x ≤ 1, (II) 1 < x ≤ 3, and (III) x > 3, but it is probably easier to just graph the number line and notice that the midpoint between 1 and 3, that is, 2, is the point at which the distance to 1 and the distance to 3 are equal. Therefore, the points that are farther from 1 than from 3 are simply the points to the right of this midpoint, or x > 2.
20. B
4x2 ≥ 9
Take square root:
|2x| ≥ 3
If x > 0:
2x ≥ 3
Divide by 2:
x ≥ 1.5
If x < 0:
2x ≤ −3
Divide by 2:
x ≤ −1.5
21. D Notice that the midpoint of the segment shown is 3, and the graph shows all points that are less than 3 units in either direction. Therefore, |x − 3| < 3.
22. B (A) is untrue if x = 0, (C) is untrue for x = −2, and (D) is untrue if x = 0.5. But (B) is true for any real number.