SAT 2016

CHAPTER 7

Skill 4: Working with Linear Systems

A system of equations is just a set of equations that apply simultaneously to a given problem situation. Solving for the system means finding all sets of values for the unknowns that make all of the equations true. Systems of equations can be analyzed both algebraically (by exploring the equations) or geometrically (by exploring the graphs).

Two high school teachers took their classes on a field trip to a museum. One class spent $154 for admission for 20 students and 3 adults, and the other class spent $188 for admission for 24 students and 4 adults. Which of the following systems of equations could be solved to determine the price of a single student admission, s, and the price of a single adult admission, a, in dollars?

A) a + s = 51

44s + 7a = 342

B) 20s + 3a = 154

24s + 4a = 188

C)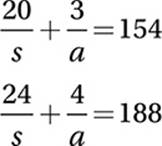

D) 20 + 24 = s

3 + 4 = a

(Medium) This problem can be described with a two-by-two system of equations, that is, two equations with two unknowns. The two equations come from two facts: one class spent $154 for admission and the other class spent $188 for admission. The cost of 20 student admissions and 3 adult admissions is 20s + 3a, so the first equation is 20s + 3a = 154. Similarly, the equation for the other class is 24s + 4a = 188, so the correct answer is (B).

y = 2x − 3

y = −2x + 17

If the solutions to the two equations above are graphed in the xy-plane, what is the y-coordinate of the point at which the graphs intersect?

(Easy) Since the equations of both lines are given in slope-intercept form, we could graph the two lines in the xy-plane to find their point of intersection.

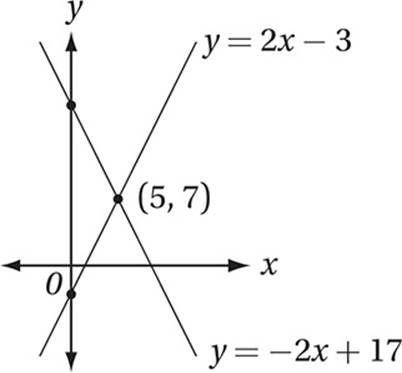
Therefore, the point (5, 7) gives us the only solution to this system, and so the answer to the original question is 7.

Alternately, (as we will see in Lesson 13) we can just add the corresponding sides of the two equations together to get 2y = 14, which yields y = 7.

The solution of a two-by-two system of equations can be visualized as the intersection of their graphs in the xy-plane.

If the graphs are parallel lines, or other non-intersecting graphs, then the system has no solution. If the graphs intersect multiple times, then the system has multiple solutions.

y − 4x = 6

16x = 4y + k

For what value of k does the system of equations above have at least one solution?

A) −32

B) −30

C) −24

D) −20

(Medium) This is a two-by-two system of linear equations, and so its solution is the intersection of those two lines. If we convert them to slope-intercept form, we get y = 4x + 6 and y = 4x − k/4, which reveals that these two lines have the same slope. This means that they are either parallel lines or identical lines. Two lines with the same slope can intersect only if they are the same line, and therefore −k/4 = 6 and k = −24.

Let”s go back to the second linear system from Lesson 11. This system can also be solved with a simple application of the Law of Substitution.

y = 2x − 3

y = −2x + 17

1. Substitute for y:

2x − 3 = −2x + 17

2. Add 2x:

4x − 3 = 17

3. Add 3:

4x = 20

4. Divide by 4:

x = 5

5. Plug into either original equation to find y:

y = 2(5) − 3 or −2(5) + 17 = 7

When one of the equations in a system is already solved for one variable (or when it”s relatively easy to solve it for one variable), then substituting for this variable in the other equation often makes it easier to solve the system.

3x + y = 3y + 4

x + 4y = 6

Based on the system of equations above what is the value of the product xy?

(Medium) This system is not quite as tidy as the previous one, but we can still solve it by using the Law of Substitution.

3x + y = 3y + 4

x + 4y = 6

Subtract 4y from second equation to isolate x:

x = −4y + 6

Substitute for x in first equation:

3(−4y + 6) + y = 3y + 4

Simplify left side:

−11y + 18 = 3y + 4

Add 11y and subtract 4:

14 = 14y

Divide by 14:

1 = y

Substitute y = 1 to find x:

x = −4(1) + 6 = 2

Evaluate xy:

xy = (2)(1) = 2

3x + 6y = 18

3x + 4y = 6

Based on the system of equations above, what is the value of y?

(Easy) Although this system can be solved by substitution (try it as an exercise), the setup of these equations suggests a much easier method, known as linear combination. It”s based on a simple idea:

The Law of Combination

If a = b and c = d, then a + c = b + d, a − c = b − d, and ac = bd

In other words, you should always feel free to add, subtract, or multiply the corresponding sides of two equations to make a new equation.

If we apply this rule to our system, notice that we can easily eliminate x from the system by just subtracting the equations:

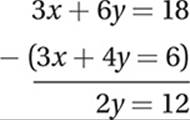
Divide by 2:

y = 6

3x − y = 20

2x + 4y = 7

Based on the system of equations above, what is the value of x − 5y?

(Medium) This question looks tougher than the previous one, because it”s not just asking for x or y. It seems that the question requires us to solve the system for x and y and then to plug these values into the expression x − 5y and evaluate. We could do that, but there is a much simpler method. Notice that a simple combination gives us the expression the question is asking for.

Using Linear Combination

When you”re given a system of equations on the SAT, always notice carefully what the question is asking you to evaluate. Even if it appears to be the value of a complicated expression, often you can find it with a simple combination of the given equations.

1

If 3x + 2y = 72, and y = 3x, what is the value of x?

2

If 2a − 7b = 10 and 2a + 7b = 2, what is the value of 4a² − 49b²?

3

If the lines y = −4x − 3 and y = −3x − b intersect at the point (−1, c), what is the value of b?

4

If the lines 4x + 5y = 13 and 4y + kx = 2 are parallel, what is the value of k?

5

If the lines 4x + 5y = 13 and 6y − kx = 6 are perpendicular, what is the value of k?

6

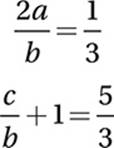
Based on the system of equations above, what is the value of ?

7

If ab = −4 and abc = 12, what is the value of ?

8

If a and b are constants and the graphs of the lines 2x − 3y = 8 and ax + by = 2 are perpendicular, then what is the value of ?

9

5x − y = 11

2x − 2y = 9

Based on the system of equations above, what is the value of 3x + y?

A) −2

B) 0

C) 2

D) 4

10

Two numbers have a difference of 4 and a sum of −7. What is their product?

A) −33

B) −10.25

C) 8.25

D) 10.25

11

It costs Emma p dollars to make each of her custom bracelets, which she sells for m dollars apiece. She makes a profit of $60 if she makes and sells 5 of these bracelets, but she only makes a profit of $10 if she makes 5 bracelets but only sells 4 of them. How much does it cost Emma to make each bracelet?

A) $36

B) $38

C) $48

D) $50

12

If 2y = x + 1 and 4x + 6y = 0, then y =

13

If 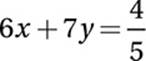and 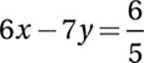, then y =

2x − 5y = 20

10x − 25y = 4k

14

For what value of k does the system of equations above have at least one solution?

15

At the beginning of the week, the ratio of cats to dogs at Glenna”s Pet Store was 4 to 5. By the end of the week, the number of cats had doubled, while the number of dogs had increased by 12. If the ratio of cats to dogs at the end of the week was 1 to 1, how many cats did the store have at the beginning of the week?

16

Jenny originally had twice as many friendship bracelets as Emilie. After Jenny gave Emilie 5 of her friendship bracelets, Jenny still had 10 more than Emilie. How many friendship bracelets did Jenny have originally?

17

The average (arithmetic mean) of x and y is 14. If the value of x is doubled and the value of y is tripled, the average (arithmetic mean) of the two numbers remains the same. What is the value of x?

18

7m + 10n = 7

6m + 9n = 1

Based on the system of equations above, what is the value of 4m + 4n?

19

In the xy-plane, perpendicular lines a and b intersect at the point (2, 2). If line a contains the point (7, 1), which of the following points is on line b?

A) (0, 1)

B) (4, 5)

C) (7, 3)

D) (3, 7)

20

Which of the following pairs of equations has no solution in common?

A) 2x − 3y = 1 and 6x − 9y = 3

B) y = 4x and y = −4x

C) 2x − 3y = 1 and 6x − 9y = 2

D) y = 4x and 2y − 8x = 0

21

In the xy-plane, the line l is perpendicular to the line described by the equation 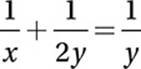. What is the slope of line l?

A) −2

B)

C)

D) 2

No Calculator

1. 8

3x + 2y = 72

Substitute y = 3x:

3x + 2(3x) = 72

Simplify:

9x = 72

Divide by 9:

x = 8

2. 20

4a² − 49b²

Factor:

(2a − 7b)(2a + 7b)

Substitute:

(10)(2) = 20

3. 2

y = −4x − 3

Substitute x = −1, y = c:

c = −4(−1) − 3

Simplify:

c = 1

Other equation:

y = −3x − b

Substitute x = −1, y = 1:

1 = −3(−1) − b

Simplify:

1 = 3 − b

Subtract 3:

−2 = −b

Divide by −1:

2 = b

4. 3.2 or 16/5 Parallel lines must have equal slopes. The slope of 4x + 5y = 13 is −4/5, and the slope of 4y + kx = 2 is −k/4.

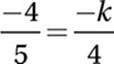
Cross-multiply:

−5k = −16

Divide by −5:

k = 16/5 = 3.2

5. 7.5 or 15/2 Perpendicular line have slopes that are opposite reciprocals. The slope of 4x + 5y = 13 is −4/5, and the slope of 6y − kx = 6 is k/6.

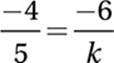
Cross-multiply:

−4k = −30

Divide by −4:

k = 7.5

6. .25 or ¼ First equation:

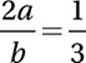
Divide by 2:

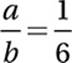
Second equation:

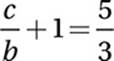
Subtract 1:

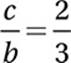
Reciprocate:

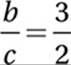
Multiply:

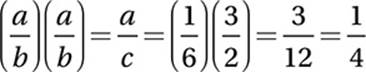
7. .75 or ¾

abc = 12

Substitute ab = −4:

(−4)c = 12

Divide by −4:

c = −3

Expression to evaluate:

Substitute c = −3 and ab = −4:

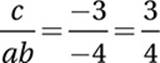
8. 4.5 or 9/2 The slope of 2x − 3y = 8 is 2/3, and the slope of ax + by = 2 is −a/b. If the two lines are perpendicular, then the slopes are

opposite reciprocals:

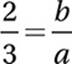
Reciprocate:

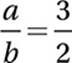
Multiply by 3:

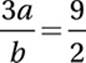
9. C

5x − y = 11

2x − 2y = 9

Subtract equations:

3x + y = 2

10. C

a − b = 4

a + b = −7

Add equations:

2a = −3

Divide by 2:

a = −1.5

Substitute a = −1.5:

−1.5 + b = −7

Add 1.5:

b = −7 + 1.5 = −5.5

Evaluate product:

ab = (−1.5)(−5.5) = 8.25

11. B Let c = the cost to make each one of Emma”s bracelets.

5m − 5c = 60

4m − 5c = 10

Subtract:

m = 50

Substitute m = 50

5(50) − 5c = 60

Simplify:

250 − 5c = 60

Subtract 250:

−5c = −190

Divide by −5:

c = 38

Calculator

12. 2/7 or .286 or .285

2y = x + 1

Subtract 1:

2y − 1 = x

Given:

4x + 6y = 0

Substitute x = 2y − 1:

4(2y − 1) + 6y = 0

Distribute:

8y − 4 + 6y = 0

Simplify:

14y − 4 = 0

Add 4:

14y = 4

Divide by 14:

y = 4/14= 2/7

13. 1/6 or .166 or .167

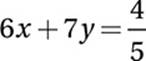
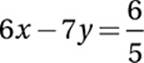
Add equations:

12x = 2

Divide by 12:

x = 2/12 = 1/6

14. 25 The slope of 2x − 5y = 20 is 2/5. The slope of 10x − 25y = 4k is 10/25 = 2/5. Since the two lines have the same slope, they have no points of intersection unless they are the same line.

2x − 5y = 20

10x − 25y = 4k

Multiply first equation by 5:

10x − 25y = 100

Therefore, 4k = 100 and so k = 25.

15. 16 If the original ratio of cats to dogs is 4 to 5, then we can say there were 4n cats and 5n dogs to start. At the end of the week, therefore, there were 8n cats and 5n + 12 dogs. If this ratio was 1:1, then

8n = 5n + 12

Subtract 5n:

3n = 12

Divide by 3:

n = 4

Therefore, there were 4n = 4(4) = 16 cats at the beginning of the week.

16. 40 Let x = the number of friendship bracelets Emilie had to start. This means that Jenny originally had 2x bracelets. After Jenny gave 5 of them to Emilie, Jenny had 2x − 5 and Emilie had x + 5. If Jenny still had 10 more than Emilie, then

2x − 5 = 10 + (x + 5)

Simplify:

2x − 5 = x + 15

Subtract x and add 5:

x = 20

This means that Jenny had 2x = 2(20) = 40 to start.

17. 56

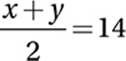
Multiply by 2:

x + y = 28

If x is doubled and y is tripled, the average remains the same:

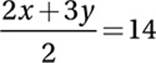
Multiply by 2:

2x + 3y = 28

Previous equation:

x + y = 28

Multiply by 3:

3x + 3y = 84

Other equation:

2x + 3y = 28

Subtract equations:

x = 56

18. 24

7m + 10n = 7

6m + 9n = 1

Subtract equations:

m + n = 6

Multiply by 4:

4m + 4n = 24

19. D Line a contains the points (2, 2) and (7, 1); therefore, it has a slope of 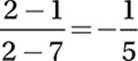. If line b is perpendicular to line a, then it must have a slope of 5 (the opposite reciprocal of −1/5). You might find it helpful to sketch the line with slope 5 through the point (2, 2), and confirm that is passes through the point (3, 7), which is one unit to the right and one 5 units up.

20. C In order for two lines in the xy-plane to have no points in common, they must be parallel and nonidentical. The only two such lines among these choices are 2x − 3y = 1 and 6x − 9y = 2, which both have a slope of 2/3, but have different y-intercepts of −1/3 and − 2/9.

21. A

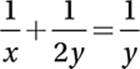
Multiply by 2xy:

2y + x = 2x

Subtract x:

2y = x

Divide by 2:

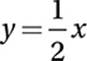
This line has a slope of 1/2, so the perpendicular must have a slope of −2.