SAT 2016
CHAPTER 10
THE SAT MATH: ADDITIONAL TOPICS
1. Understanding Geometric Relationships
2. Understanding Basic Trigonometry
3. Understanding Complex Numbers

The SAT Math: Additional Topics
What other special topics are included on the SAT Math test?
About 10% (6 out of 58 points) of the SAT Math questions are “Additional Topics” questions. These include topics like
• analyzing triangles using the Pythagorean Theorem
• graphing circles and other figures in the xy-plane
• analyzing areas, circumferences, chords, and sectors of circles
• measuring angles and arcs in radians
• working with area and volume and their formulas
• using the theorems of congruence and similarity
• working with basic trigonometric relationships including cofunction identities
• calculating with imaginary and complex numbers
Why are these topics important?
These topics from geometry, trigonometry, and advanced analysis are crucial to work in engineering, physics, architecture, and even design. Although they are not essential to every college major, they do provide tools for understanding and analyzing advanced concepts across the curriculum.
Sound intimidating? It”s not.
Some of you have already spent some time in math class studying these topics. If not, the three skills described in these 12 lessons will give you the knowledge and practice you need to master them.
Skill 1: Understanding Geometric Relationships
Lesson 1: Intersecting and parallel lines
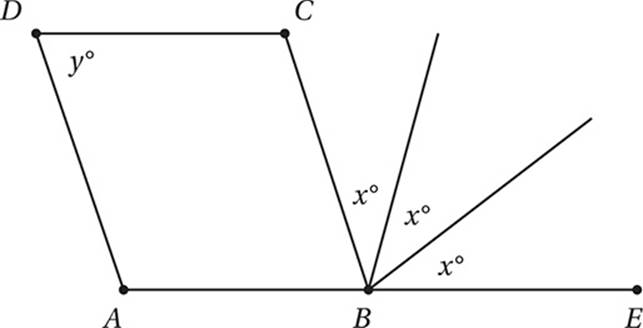
In the figure above, ABCD is a parallelogram, and point B lies on ![]() . If x = 40, what is the value of y?
. If x = 40, what is the value of y?
A) 40
B) 50
C) 60
D) 70
(Medium) Since ABCD is a parallelogram, we can take advantage of the Parallel Lines Theorem.
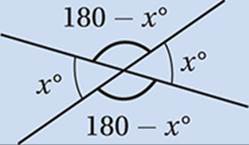
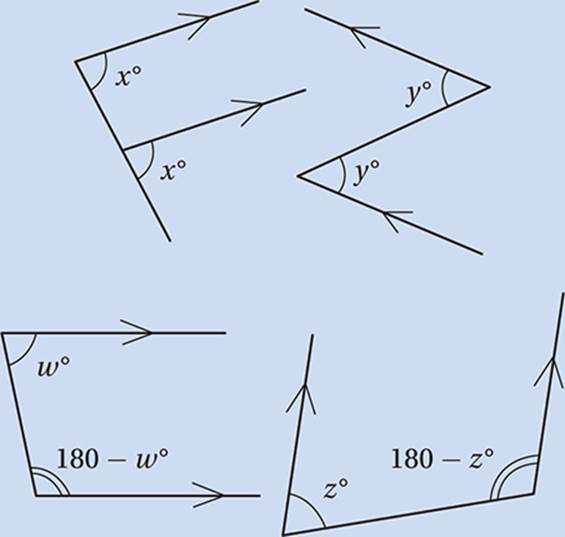
The Intersecting Lines Theorem
When two lines cross, four angles are formed. The vertical angles are congruent and adjacent angles are supplementary (that is, they have a sum of 180°).
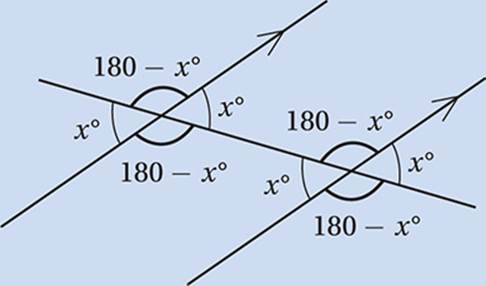
The Parallel Lines Theorem
When two parallel lines are crossed by a third line, eight angles are formed. If the third line is perpendicular to one of the parallel lines, then it”s perpendicular to the other and all eight angles are right angles. Otherwise, all four acute angles are congruent, all four obtuse angles are congruent, and any acute angle is supplementary to any obtuse angle.
Helpful Tip
When dealing with parallel lines, especially in complicated figures, we can simplify things by considering angles in pairs. The important pairs form one of four letters: F, Z, C, or U.
First, let”s mark up the diagram with what we know from the Parallel Lines Theorem.
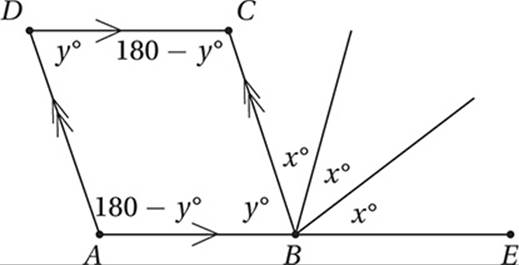
Since the pairs of opposite sides are parallel, the consecutive angles in the parallelogram must be supplementary (that is, have a sum of 180°). Notice that these pairs of consecutive angles form “U”s or “C”s as mentioned in the previous Helpful Tip. This implies that opposite angles are congruent in a parallelogram.
Since ![]() is a straight (180°) angle:
is a straight (180°) angle:
y + x + x + x = 180
Substitute x = 40 and simplify:
y+ 120 = 180
Subtract 120:
y = 60
Therefore, the correct answer is (C).
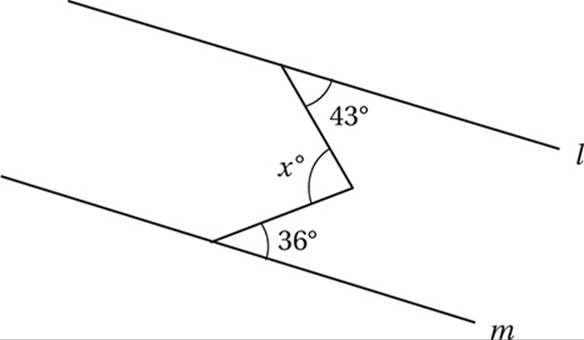
In the figure above, lines l and m are parallel. What is the value of x?
A) 43
B) 79
C) 86
D) 101
(Hard) Although our diagram includes parallel lines, it doesn”t seem to show any of the parallel line “letter pairs” that we discussed above, because no line directly connects the parallel lines. We can fix this problem by drawing an extra line that”s parallel to l and m through the vertex of the angle.
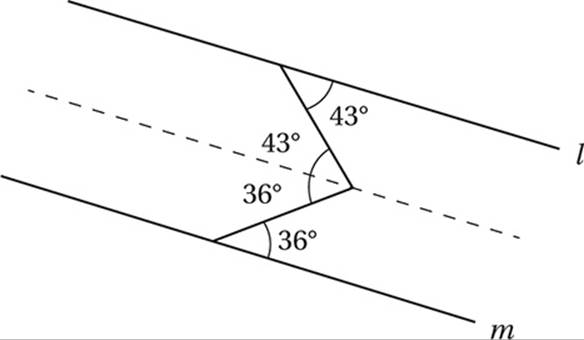
Now we have two “Z” pairs of angles (otherwise known as “alternate interior” pairs) that show that the middle angle is actually the sum of two smaller angles of 36° and 43°, and therefore, x = 36 + 43 = 79, and the correct answer is (B).
Lesson 2: Triangles
Angle Sum Theorem
The sum of the measures of the angles in any triangle is 180°.
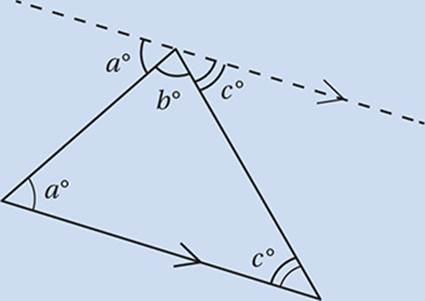
We can prove this with the “draw an extra line” trick. If we take any triangle, pick any of its vertices, and draw a line through that vertex that is parallel to the opposite side, we get a picture like the one above. Since the line we”ve drawn is a 180° angle, and since the “Z” angle pairs must be congruent, we”ve proven that a + b + c = 180.
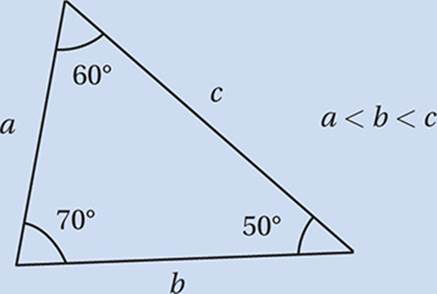
Side-Angle Theorem
The largest angle in a triangle is always across from the largest side, and the smallest angle is always across from the smallest side.
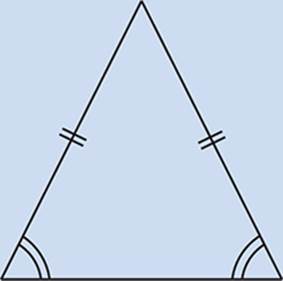
Isosceles Triangle Theorem
If two sides in a triangle are congruent, the two angles across from those sides are also congruent. Conversely, if two angles in a triangle are congruent, the two sides across from them are also congruent.
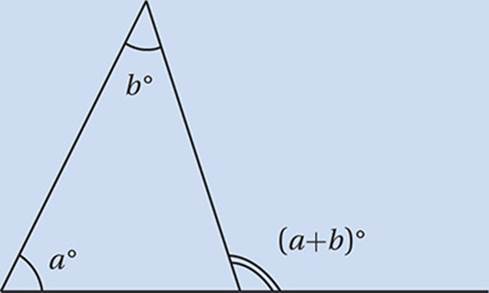
Exterior Angle Theorem
If the side of a triangle is extended beyond a vertex, it makes an exterior angle with the adjacent side. The measure of this exterior angle is equal to the sum of the two remote interior angles.
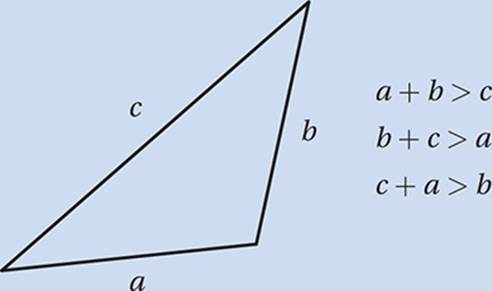
The Triangle Inequality
The sum of any two sides of a triangle must always be greater than the third side.
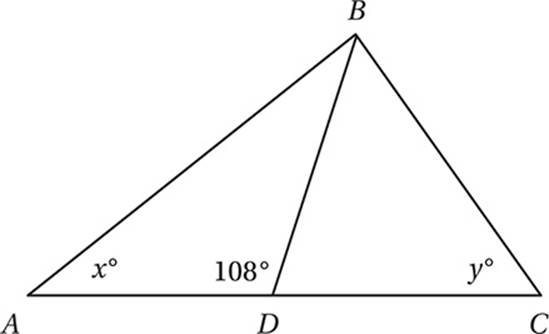
In the figure above, if AD = DB = DC, what is the value of x + y?
A) 72
B) 90
C) 96
D) 108
(Medium) Since angle ADB and angle BDC are supplementary and AD = DB = DC, we can take advantage of the Isosceles Triangle Theorem to mark up the diagram.
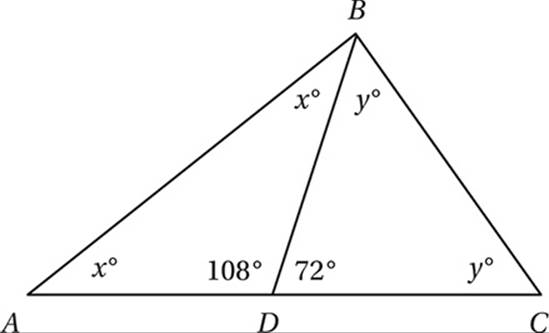
Now let”s look at triangle ABC. Since its interior angles must have a sum of 180°, x + x + y + y = 180, and therefore, 2x + 2y = 180 and x + y = 90. So the correct answer is (B). Notice that this fact is independent of the measures of the other two (108° and 72°) angles. As long as AD = DB= DC, this relationship will hold. We can see these angle relationships if we notice that these three segments could all be radii of a circle centered at D.
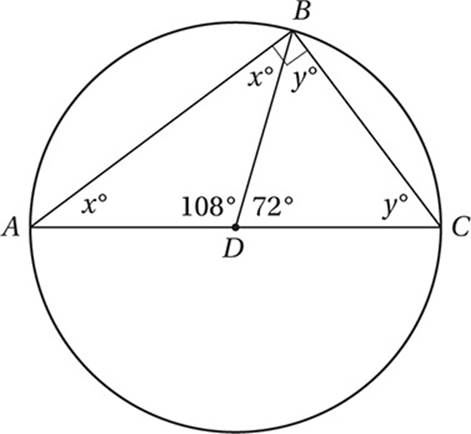
You may remember from studying geometry that any “inscribed” angle (an angle inside a circle with a vertex on the circle) intercepts an arc on the circle that is twice its measure. Since angle ABC is an inscribed angle that intercepts a 180° arc, it must have a measure of 90° and therefore,x + y = 90.
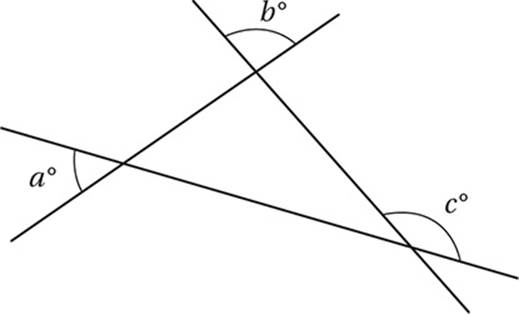
The figure above shows three intersecting lines. What is the value of c in terms of a and b?
A) 180 − a − b
B) 180 − a + b
C) 90 + b − a
D) a + b
(Easy) First, we should notice that two of the angles are “vertical” to two interior angles of the triangle, and the other is an exterior angle.
Since the c° angle is an exterior angle to the triangle, the Exterior Angle Theorem tells us that c = a + b, so the correct answer is (D).
Alternately, we could just choose reasonable values for a and b, like a = 50 and b = 90, and then analyze the diagram in terms of these values. This would imply that the interior angles of the triangle are 50°, 90°, and 40°, and c° would then be the measure of the supplement of 40°, which is 140°. If we then plug these values for a and b into all of the choices, the only one that yields 140 is D.
Lesson 3: The xy-plane
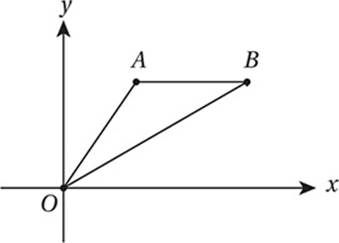
Note: Figure not drawn to scale.
In the xy-plane above, points A and B lie on the graph of the line y = 6. If OB has a slope of ![]() and AB = 5, what is the slope of
and AB = 5, what is the slope of ![]() ?
?

(Medium-hard) To analyze this diagram, we must recall the definition of slope from Chapter 7, Lesson 5.
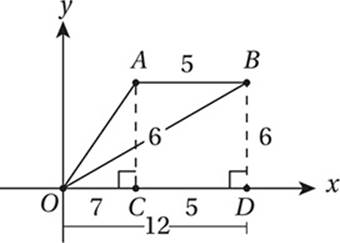
First, let”s drop two perpendicular segments from A and B to points C and D, respectively, on the x-axis. Since A and B lie on the line y = 6, they are both 6 units from the x-axis, and so AC = BD = 6. Then, since the slope of OB is ½, BD/OD = ½, and therefore, OD = 12. Since AB = 5, CD= 5 also, and therefore, OC = 12 – 5 = 7. (Don”t worry that ![]() looks shorter than
looks shorter than ![]() in the diagram. Remember, the figure is not drawn to scale!) This gives us everything we need to find the slope of
in the diagram. Remember, the figure is not drawn to scale!) This gives us everything we need to find the slope of ![]() , which connects (0, 0) to (7, 6). By the slope formula from Chapter 7, Lesson 5, slope = (6 – 0)/(7 – 0) = 6/7 = 0.857.
, which connects (0, 0) to (7, 6). By the slope formula from Chapter 7, Lesson 5, slope = (6 – 0)/(7 – 0) = 6/7 = 0.857.
Working in the Coordinate Plane
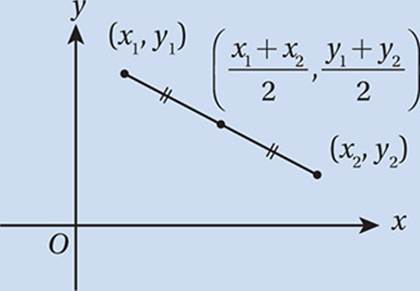
Finding Segment Midpoints. To find the coordinates of a midpoint, just average the coordinates of the endpoints.
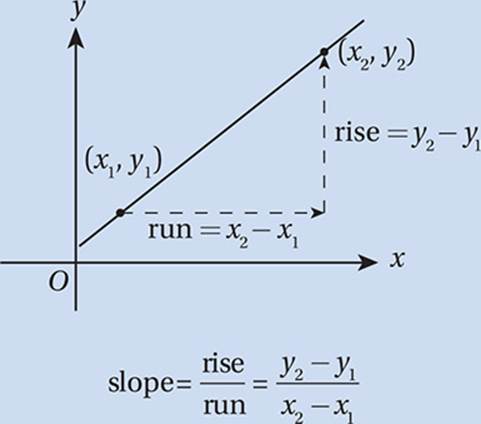
Finding Slopes. To find the slope of a line in the xy-plane from any two points on the line, use the slope formula.
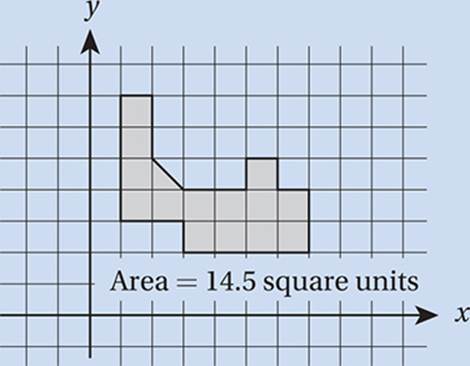
Finding Areas. Remember that the area of a figure is just the number of unit squares that fit inside it. You don”t always need to use a special formula to find the area of a figure. Even for very complicated shapes, you can sometimes find the area just by counting squares.
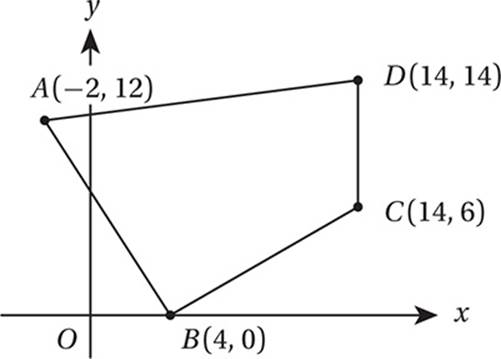
In the figure above, point M (not shown) is the midpoint of ![]() and point N (not shown) is the midpoint of
and point N (not shown) is the midpoint of ![]() . What is the slope of
. What is the slope of ![]() ?
?

(Medium) To find the midpoint of a segment, we just need to take the average of the endpoints. Point M, the midpoint of ![]() , therefore has coordinates
, therefore has coordinates 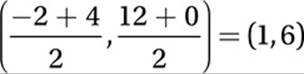 , and point N, the midpoint of %
, and point N, the midpoint of %![]() , has coordinates
, has coordinates 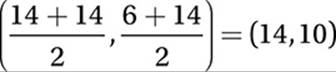 . By the Slope Formula, then, the slope of
. By the Slope Formula, then, the slope of ![]() is
is 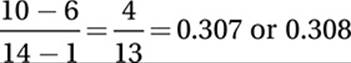 .
.
Lesson 4: The Pythagorean Theorem and the Distance Formula
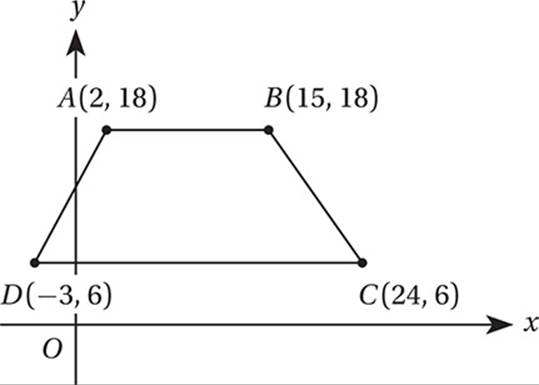
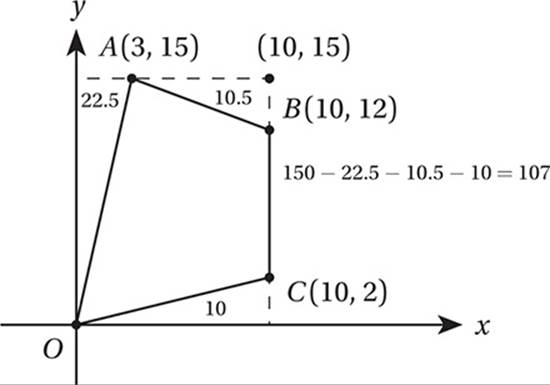
What is the perimeter of quadrilateral ABCD in the figure above?

(Medium) The perimeter of a figure is the distance around its edges. It”s easy to find the lengths of ![]() and
and ![]() because they are horizontal. The length of a horizontal segment is just the difference between the x-coordinates of its endpoints. The length of
because they are horizontal. The length of a horizontal segment is just the difference between the x-coordinates of its endpoints. The length of ![]() is 15 – 2 = 13, and the length of
is 15 – 2 = 13, and the length of ![]() is 24 – (–3) = 27. To find the lengths of
is 24 – (–3) = 27. To find the lengths of ![]() and
and ![]() , we can drop two vertical lines from points A and B to the bottom edge. This shows that
, we can drop two vertical lines from points A and B to the bottom edge. This shows that ![]() and
and ![]() are hypotenuses of two right triangles as shown in the figure below.
are hypotenuses of two right triangles as shown in the figure below.
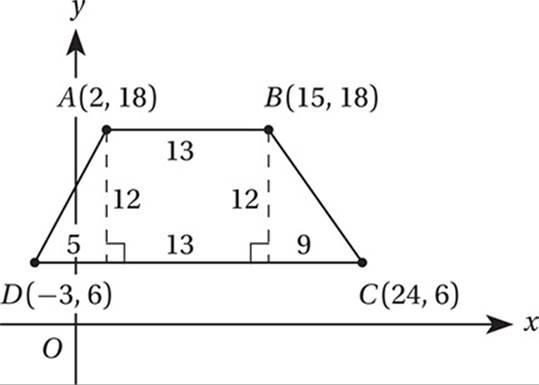
(Take a minute to confirm the lengths of all the segments for yourself.) With this information, we can find AD and BC by the Pythagorean Theorem.
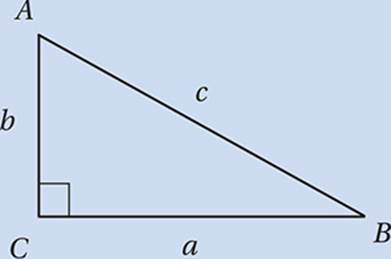
The Pythagorean Theorem
If a, b, and c represent the sides of a right triangle in which c is the longest side (the hypotenuse),
a2 + b2 = c2
Special Right Triangles
The SAT Math test expects you to be familiar with four families of special right triangles: 45°-45°-90° triangles, 30°-60°-90° triangles, 3-4-5 triangles, and 5-12-13 triangles. Take some time to familiarize yourself with these particular side-side relationships and side-angle relationships so that you can use these relationships when you recognize these triangles in SAT Math questions.
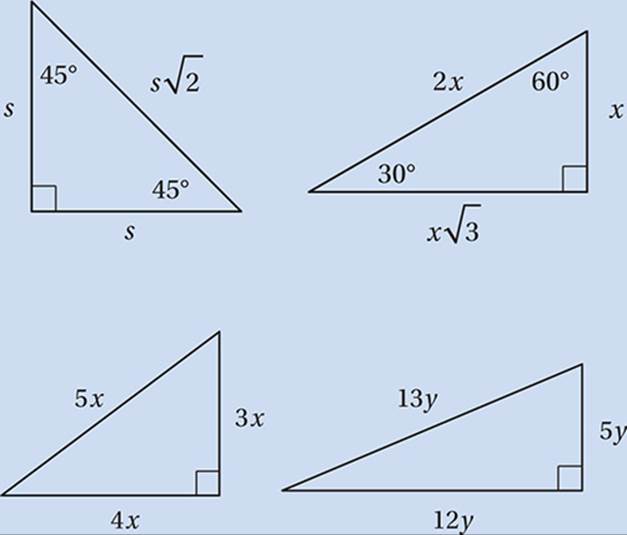
(3x)2 + (4x)2 = (5x)2
9x2 + 16x2 = 25x2
(5y)2 + (12y)2 = (13y)2
25y2 + 144y2 = 169y2
So, according to our diagram:
AD2 = 52 + 122 = 169
BC2 = 92 + 122 = 225
Notice that triangle on the left is a 5-12-13 special right triangle, and the triangle on the right is a 3-4-5 special right triangle. Noticing these relationships provides a shortcut to using the Pythagorean Theorem.
Take the square root:
AD = 13
BC = 15
Therefore, the perimeter of ABCD is 13 + 15 + 27 + 13 = 68.
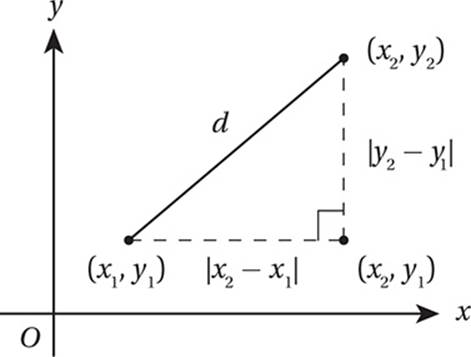
The Distance Formula
![]()
We can generalize the technique we used in the previous problem to find the distance between any two points in the xy-plane. Just think of this distance as the length of the hypotenuse of a right triangle, as in the figure below. In other words, the Pythagorean Theorem and the Distance Formula are one and the same.

The 3-D Distance Formula
![]()
If we need to find the distance between two points in three-dimensional xyz-space, we just need to use a modified version of the distance formula that includes the extra z-dimension. You can see where this formula comes from if you imagine trying to find the length of the longest diagonal through a rectangular box.
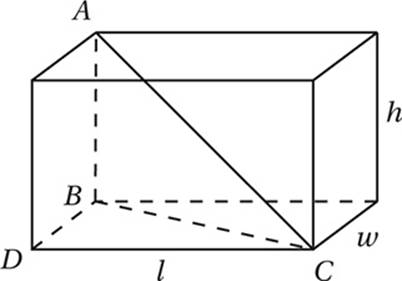
The length of this diagonal, AC, is also the hypotenuse of right triangle ABC, and so its length is given by the Pythagorean Theorem.

Exercise Set 1: Geometry (No Calculator)
1
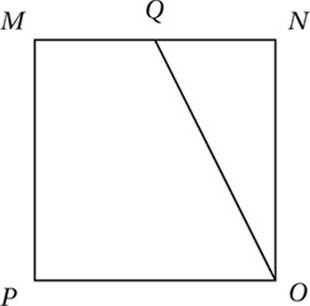
In the figure above, MNOP is a square and Q is the midpoint of ![]() . If
. If 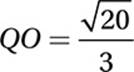 , what is the area of square MNOP?
, what is the area of square MNOP?

2
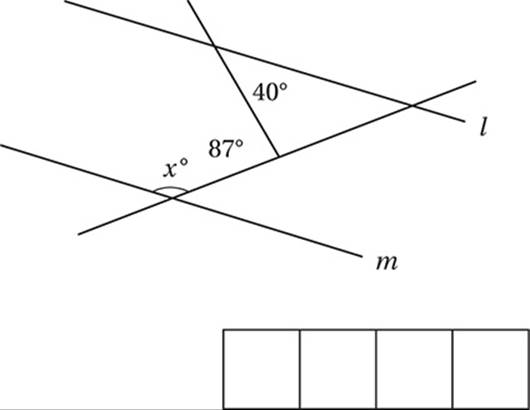
Lines l and m are parallel in the figure above. What is the value of x?
3
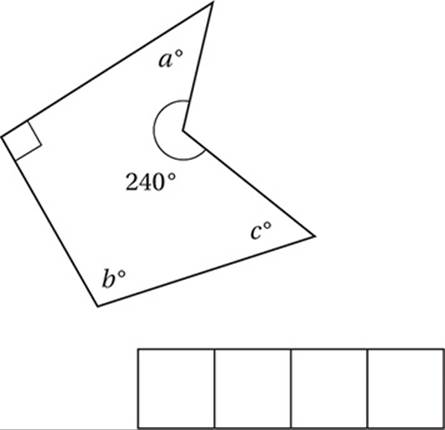
In the figure above, what is the value of a + b + c?
4
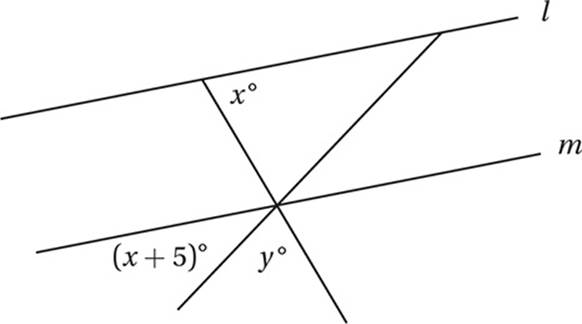
Lines l and m are parallel in the figure above. Which of the following expresses the value of y in terms of x?
A) 95 – 2x
B) 165 – 2x
C) 175 – 2x
D) 185 – 2x
5
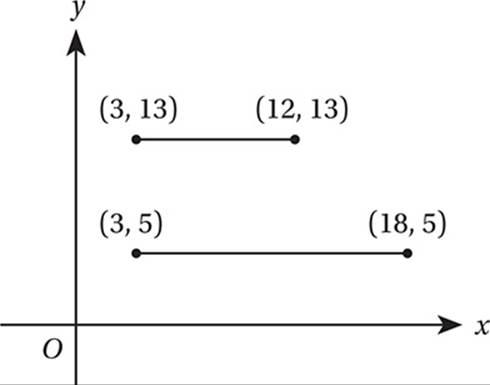
In the figure above, what is the distance between the midpoints (not shown) of the two line segments?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
6
What is the perimeter of an equilateral triangle inscribed in a circle with circumference 24π?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Exercise Set 1: Geometry (Calculator)
Questions 7–9 are based on the figure below.
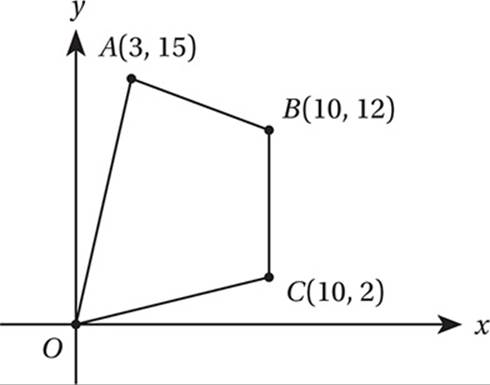
Note: Figure not drawn to scale.
7
In the figure above, what is the perimeter of quadrilateral ABCO, to the nearest integer?

8
In the figure above, what is the area, in square units, of ABCO?

9
In the figure above, point K (not shown) is the midpoint of ![]() , and point M (not shown) is the midpoint of
, and point M (not shown) is the midpoint of ![]() . What is the slope of
. What is the slope of ![]() ?
?

10
In the xy-plane, point H has coordinates (2, 1) and point J has coordinates (11, 13). If ![]() is parallel to the x-axis and
is parallel to the x-axis and ![]() is parallel to the y-axis, what it the perimeter of triangle HJK?
is parallel to the y-axis, what it the perimeter of triangle HJK?

11
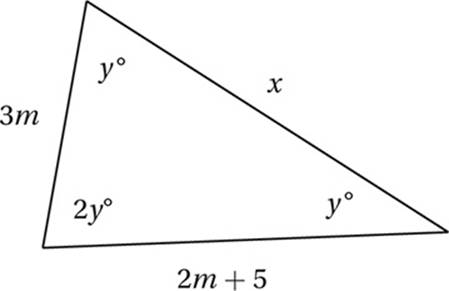
Note: Figure not drawn to scale.
In the figure above, what is the value of x?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
![]()
Questions 12–15 are based on the situation described below.
In the xy-plane, ABCD is a square. Point A has coordinates (–1, 2) and point B has coordinates (3, 5).
12
Which of the following could be the coordinates of C?
A) (0, 9)
B) (6, 0)
C) (2, –2)
D) (–4, 6)
13
What is the area of square ABCD?
A) 25
B) 28
C) 30
D) 32
14
What is the slope of ![]() ?
?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
15
What is the distance between C and the midpoint of ![]() ?
?
A) 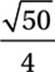
B) 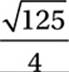
C) 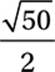
D) 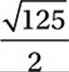
![]()
EXERCISE SET 1: GEOMETRY ANSWER KEY
No Calculator
1. 16/9 or 1.77 or 1.78 If we define x as the length of ![]() , then the length of one side of the square is 2x, and so the area of square MNOP is (2x)(2x) = 4x2. To find this value, we can apply the Pythagorean Theorem to right triangle QNO:
, then the length of one side of the square is 2x, and so the area of square MNOP is (2x)(2x) = 4x2. To find this value, we can apply the Pythagorean Theorem to right triangle QNO:
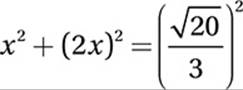
Simplify:
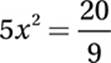
Divide by 5:
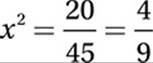
Multiply by 4:
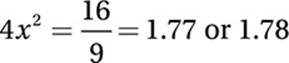
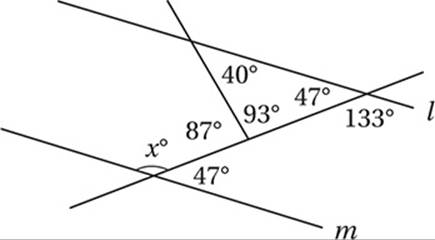
2. 133 The key is to notice simple relationships between angles until we get around to x
3. 210 Draw three lines as shown:
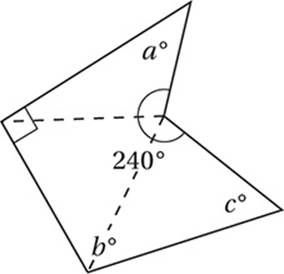
Since the polygon divides into 3 triangles, the sum of its internal angles is (3)(180°) = 540°. Therefore a + b + c + 240 + 90 = 540, and so a + b + c = 210.
4. C Using the Crossed Lines Theorem and the Parallel Lines Theorem, we can mark up the diagram like this:
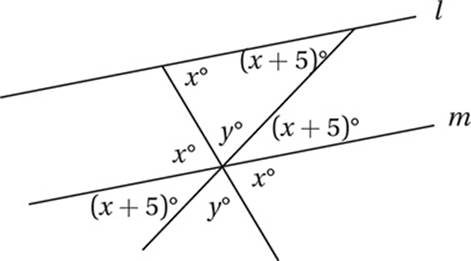
This shows that x + y + x + 5 = 180, and so y = 175 – 2x.
5. B The midpoint of the top segment is 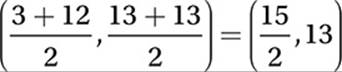 , and the midpoint of the bottom segment is
, and the midpoint of the bottom segment is 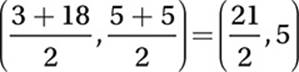 , therefore, the distance between them is
, therefore, the distance between them is 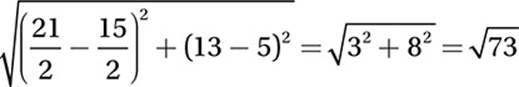
6. C To solve this problem we must draw a diagram and find the relationship between the radius of the circle and the sides of the triangle. By the Isosceles Triangle Theorem, if all three sides of a triangle are congruent, then all three angles must be congruent. Since these angles also must have a sum of 180°, they must each be 60°. If we draw the bisectors of each of these angles, we divide the triangle into six smaller triangles. These smaller triangles are congruent 30°-60°-90 ° triangles, as shown here:
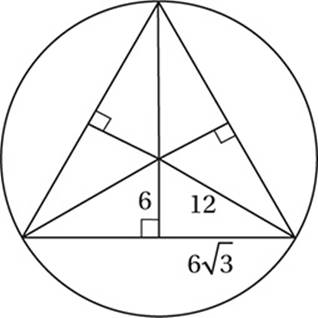
Since the circumference of the circle (2πr) is 24π, its radius is 12. Since each of the hypotenuses of our right triangles is also a radius of the circle, we can find all of the sides of these triangles using the 30°-60°-90° relationships. Each side of the equilateral triangle is therefore ![]() , and its perimeter is therefore
, and its perimeter is therefore 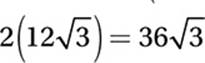 .
.
Calculator
7. 43 Using the distance formula, we can calculate the lengths of each segment. ![]() ,
, ![]() , and
, and ![]() . Therefore, the perimeter is approximately 15.30 + 7.61 + 10 + 10.20 = 43.11, which rounds to 43.
. Therefore, the perimeter is approximately 15.30 + 7.61 + 10 + 10.20 = 43.11, which rounds to 43.
8. 107 Since we do not have a formula that directly calculates the area of such an odd-shaped quadrilateral, we must analyze its area in terms of simpler shapes. The simplest way to do this is by drawing a box around it. This turns the area of interest into a rectangle minus three right triangles, all of which have areas that can be easily calculated.
9. 6/5 or 1.2 The midpoint of ![]() is (1.5, 7.5) and the midpoint of
is (1.5, 7.5) and the midpoint of ![]() is (6.5, 13.5); therefore, the slope of the segment between them is 6/5.
is (6.5, 13.5); therefore, the slope of the segment between them is 6/5.
10. 36 If point K is on the same horizontal line as (2, 1), it must have a y-coordinate of 1, and if it is on the same vertical line as (11, 13), it must have an x-coordinate of 11. Therefore, K is the point (11, 1), and so HK = 9, JK = 12, and ![]() . Notice that it is a 3-4-5 triangle!
. Notice that it is a 3-4-5 triangle!
11. C Since the sum of the interior angles of any triangle is 180°, y + y + 2y = 4y = 180, and therefore y = 45. Therefore, this is a 45°-45°-90° right triangle. Since two angles are equal, the two opposite sides must also be equal, so 3m = 2m + 5 and so m = 5 and the two legs each have measure 15. Using the Pythagorean Theorem or the 45°-45°-90 ° shortcut, we can see that ![]() .
.
12. A The key to questions 12 through 15 is a good diagram in the xy-plane that represents the given information:
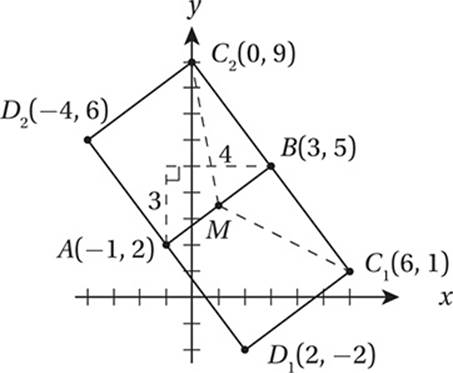
If ABCD is a square, then the points A, B, C, and D must appear in that order around the square. Notice that to get from point A to point B, we must move 4 units to the right and 3 units up. This means that, in order to get to point C along a perpendicular of the same length, we must go either3 units right and 4 units down, or 3 units left and 4 units up. This puts us either at (6, 1) or (0, 9).
13. A The diagram shows that AB is the length of the hypotenuse of a right triangle with legs 3 and 4. You should recognize this as the special 3-4-5 right triangle. If AB = 5, then the area of the square is 52 = 25.
14. A Notice that the slope of ![]() is the same regardless of which option we choose for C. In either case, the slope formula tells us that the slope is −4/3.
is the same regardless of which option we choose for C. In either case, the slope formula tells us that the slope is −4/3.
15. D The midpoint of ![]() (point M above) is (1, 3.5). We can use the distance formula to find the distance between this point and either of the possible locations of C. (Notice that the distance is the same either way.) Alternately, we might notice that MC is the hypotenuse of a right triangle with legs 5 and 2.5. Either way, we get a value of
(point M above) is (1, 3.5). We can use the distance formula to find the distance between this point and either of the possible locations of C. (Notice that the distance is the same either way.) Alternately, we might notice that MC is the hypotenuse of a right triangle with legs 5 and 2.5. Either way, we get a value of 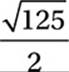 .
.
Lesson 5: Circles
Which of the following equations represents a circle in the xy-plane that passes through the point (1, 5) and has a center of (3, 2)?
A) ![]()
B) (x – 3)2 + (y – 2)2 = 13
C) (x – 1)2 + (y – 5)2 = 13
D) (x – 3)2 + (y – 2)2 = 25
Equations of Circles
(x – h)2 + (y – k)2 = r2
A circle is defined as the set of all points in a plane that are a fixed distance, r, from a fixed point, (h, k). The distance r is called the radius and (h, k) is the center.
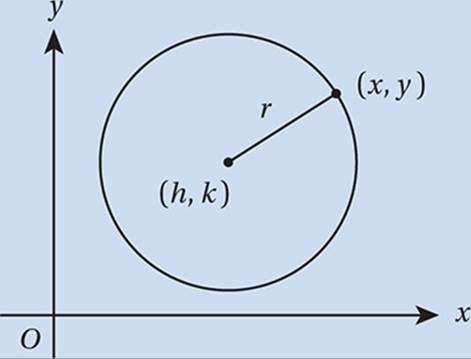
Therefore, by the Distance Formula, any point (x, y) on the circle must satisfy the equation
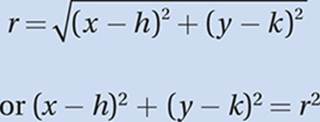
(Easy) Since our circle has a center at (3, 2), its equation must have the form (x – 3)2 + (y – 2)2 = r2, which eliminates choice (C). To find r, the radius, we simply have to find the distance between the center and any point on the circle. By the distance formula, this is ![]() , and therefore,
, and therefore, 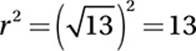 . The correct answer is (B). If you chose (A), keep in mind that the equation for a circle has r2 on the right side, not r.
. The correct answer is (B). If you chose (A), keep in mind that the equation for a circle has r2 on the right side, not r.
What is the area, in square centimeters, of a circle with circumference of 16π centimeters?
A) 8π
B) 16π
C) 32π
D) 64π
(Easy) If the circumference of the
circle is 16π centimeters:
2πr = 16π
Divide by 2π:
r = 8
Therefore, by the area formula:
Area = πr2 = π(8)2 = 64π
So the correct answer is (D).
Circumference of a Circle
circumference = πd = 2πr
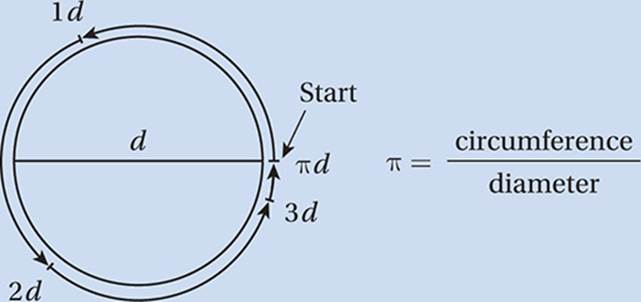
The number π (≈ 3.14159 …) is defined as the number of diameters it takes to get around a circle. Put another way, π is the ratio of the circumference of any circle to its diameter. Since any diameter is twice the radius,
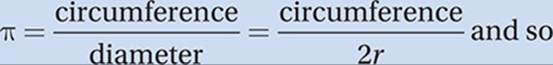 circumference = 2πr
circumference = 2πr
Area of a Circle
A = πr2
If we cut any circle into tiny enough sectors, and reassemble them as shown below, we can create a parallelogram-like shape that has a height of r and a length that is half of the circumference, or πr.
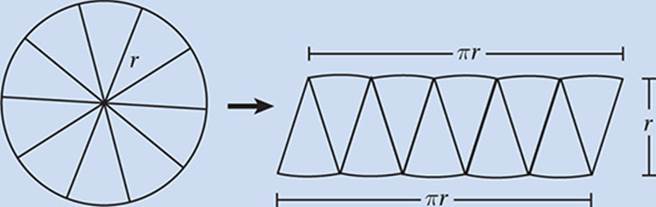
Since the area of any parallelogram is equal to its base times its height, the area of a circle is (πr)(r) = πr2.
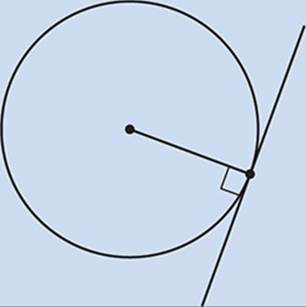
Tangents to Circles
A tangent line to a curve is a line that touches the curve without crossing it. A tangent line to any circle is perpendicular to the radius at the point of tangency.
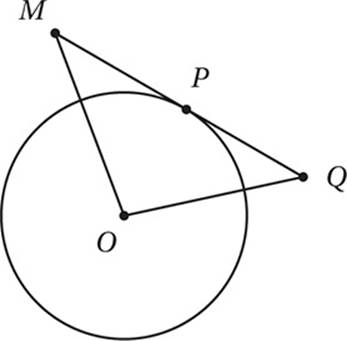
In the figure above, ![]() is tangent to the circle at point P,
is tangent to the circle at point P, ![]() , and
, and ![]() . If the circle has an area of 100π, what is the area of triangle MOQ?
. If the circle has an area of 100π, what is the area of triangle MOQ?

(Hard) The first thing we should do is draw radius ![]() . Since this is a radius to the point of tangency, it is perpendicular to the tangent. We should also write in the given measures.
. Since this is a radius to the point of tangency, it is perpendicular to the tangent. We should also write in the given measures.
The area of the circle is 100π:
π(OP)2 = 100π
Divide by π:
(OP)2 = 100
Take square root:
OP = 10
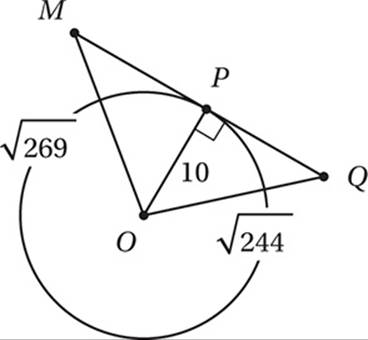
Notice that ![]() is the height of triangle MOQ if
is the height of triangle MOQ if ![]() is taken as its base. If we can find the length of base
is taken as its base. If we can find the length of base ![]() , we can simply use the triangle angle formula
, we can simply use the triangle angle formula 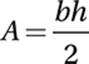 . To find MQ, we can use the Pythagorean Theorem to find MP and PQ and just add them together.
. To find MQ, we can use the Pythagorean Theorem to find MP and PQ and just add them together.
Pythagorean Theorem for triangle OPM:
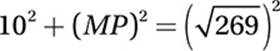
Pythagorean Theorem for triangle OPQ:
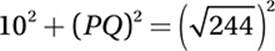
Simplify:
100 + (MP)2 = 269
100 + (PQ)2 = 244
Subtract 100:
(MP)2 = 169
(PQ)2 = 144
Take square root:
MP = 13
PQ = 12
Therefore MQ =
MP + PQ =
13 + 12 = 25, so:
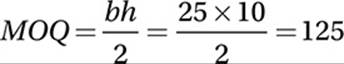
Lesson 6: Radians, chords, arcs, and sectors
What is the degree measure of an angle that measures 4.5 radians?
A) 4.5π°
B) ![]()
C) 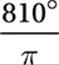
D) ![]()
(Medium) Although many students will get this question wrong, it is very simple if you know how to convert radians to degrees. All we need to do to convert any radian measure to a degree measure is to multiply it by the conversion factor 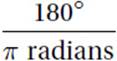 (as explained below). Therefore,
(as explained below). Therefore, 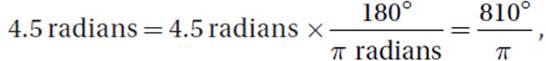 and the correct answer is (C).
and the correct answer is (C).
The Radian
A radian is simply the radius of a circle used as a “measuring stick” for an arc on the circle and for its corresponding central angle.
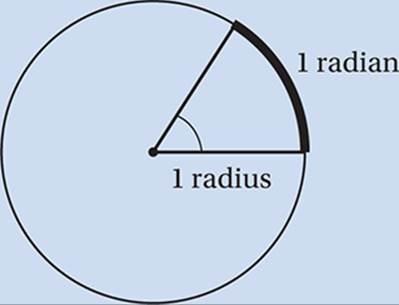
Because circumference = 2πr, a full rotation of 360° equals 2π radians, and 180° equals π radians.
Therefore, we may use  as a conversion factor to convert a degree measure to radians, and
as a conversion factor to convert a degree measure to radians, and  as a conversion factor to convert a radian measure to degrees.
as a conversion factor to convert a radian measure to degrees.


Take some time to memorize the radian measures of the common degree measures above. Put them on flashcards and study them until you”ve mastered them.
The circle above has an area of 100π square centimeters. If chord ![]() is 8 centimeters long, how far, in centimeters, is
is 8 centimeters long, how far, in centimeters, is ![]() from the center of the circle?
from the center of the circle?
A) 6
B) 8
C) ![]()
D) ![]()
(Medium) First, let”s draw three extra line segments:
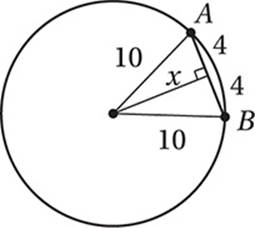
Since πr2 = 100π, r = 10. If we draw a perpendicular from the center to the chord, the length of this segment is the distance from the center to the chord. This segment also bisects the chord, dividing it into two equal segments of 4 centimeters each. This allows us to use the Pythagorean Theorem to find this distance:
42 + x2 = 102
Simplify:
16 + x2 = 100
Subtract 16:
x2 = 84
Take square root:
![]()
Therefore, the correct answer is (D).
Chords
A chord is any line segment that connects two points on a circle. The longest chord in a circle is its diameter, which passes through the center.
The perpendicular segment from the center of the circle to a chord always bisects that chord.
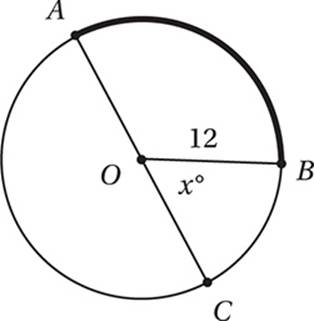
Note: Figure not drawn to scale.
In the figure above, AC is a diameter of the circle with center O, OB = 12, and the length of arc AB is 7π. What is the value of x?
A) 60
B) 72
C) 75
D) 78
(Medium) Since the circle has a radius of 12, its circumference is 2π(12) = 24π. Since AC is a diameter, then the measure of arc AC is half the circumference, or 12π. If the length of arc AB is 7π, then the length of arc BC is 12π – 7π = 5π. Since the central angle of x° is the same fraction of 360° as its arc BC is to the
entire circumference,
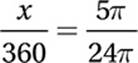
Cross multiply:
24πx = 1,800π
Divide by 24π:
x = 75
Therefore, the correct answer is (C).
Arcs and Sectors
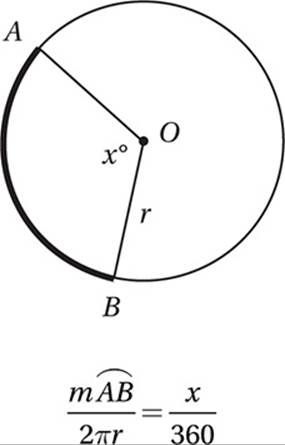
An arc is a continuous part of the circumference of a circle. Every arc has a corresponding central angle. The ratio of an arc length to the circumference is equal to the ratio of its central angle to 360° (or, in radians, 2π).
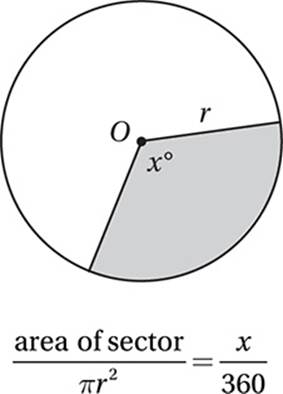
A sector is a part of the interior of a circle bounded by an arc and two radii. The ratio of a sector area to the area of the circle is equal to the ratio of its central angle to 360° (or, in radians, 2π).
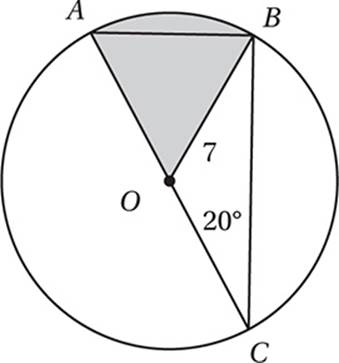
Note: Figure not drawn to scale.
In the figure above, AC is a diameter of the circle with center O, OB = 7, and the measure of ACB is 20°. What is the area of the shaded sector?
A) 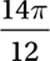
B) 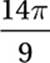
C) 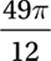
D) 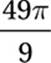
(Medium-Hard) Since ![]() ,
, ![]() , and
, and ![]() are all radii, triangles AOB and BOC are isosceles. Therefore, we can analyze the diagram with the Isosceles Triangle Theorem and the Angle Sum Theorem:
are all radii, triangles AOB and BOC are isosceles. Therefore, we can analyze the diagram with the Isosceles Triangle Theorem and the Angle Sum Theorem:
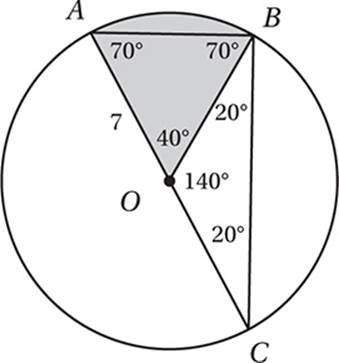
Since the central angle of the sector is 40°, the area of the sector is 40°/360° = 1/9 the area of the circle. Since the area of the circle is π(7)2 = 49π, the area of the sector is 49π/9 square units. Therefore, the correct answer is (D).
Lesson 7: Areas and volumes
Reference Information
Every SAT Math section will include the following Reference Information. Take some time to familiarize yourself with these area and volume formulas.
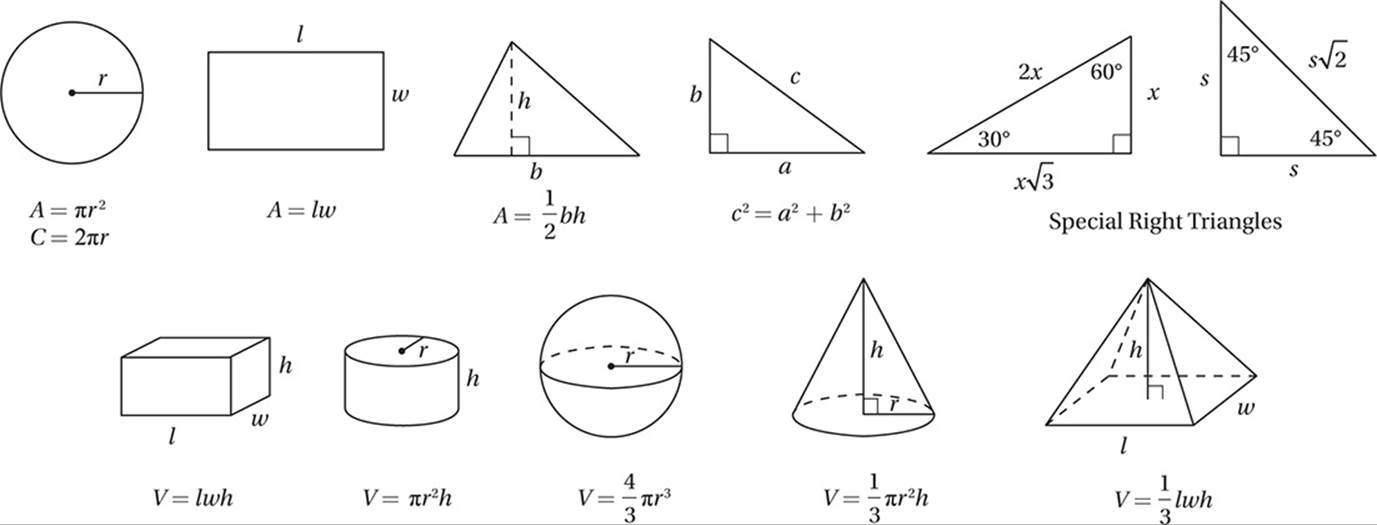
The number of degrees of arc in a circle is 360.
The number of radians of arc in a circle is 2π.
The sum of the measures in degrees of the angles of a triangle is 180.
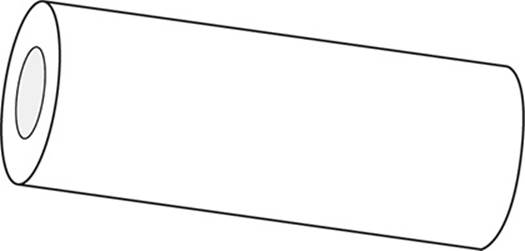
The figure above shows a wooden cylindrical tube with a length of 10 centimeters and a diameter of 4 centimeters with a cylindrical hole with a diameter of 2 centimeters that extends 40% of the length of the tube. The tube is closed on the end opposite to the hole. The density of the wood is 4.2 grams per cubic centimeter. What is the mass of this tube, to the nearest gram? (Recall that mass = density × volume)
A) 151 grams
B) 343 grams
C) 468 grams
D) 475 grams
(Medium) To find the mass of the tube, we must multiply its density by its volume. To find its volume, we must subtract the volume of cylindrical hole from the volume of the wooden cylinder. The large cylinder has a radius of 2 (remember, the diameter is 4 and so the radius is 4 ÷ 360° = 360°) and a length of 10, so its volume is π(360°)2(10) = 40π. The cylindrical hole has a radius of 1 (because its diameter is 2) and a length of (0.40)(10) = 4, so the volume of the hole is π(1)2(4) = 4π. Therefore the total volume of the closed tube is 40π – 4π = 36π ≈ 113.1. Since the mass is equal to the volume times the density, its mass is (113.1)(4.2) = 475 grams, so the correct answer is (D).
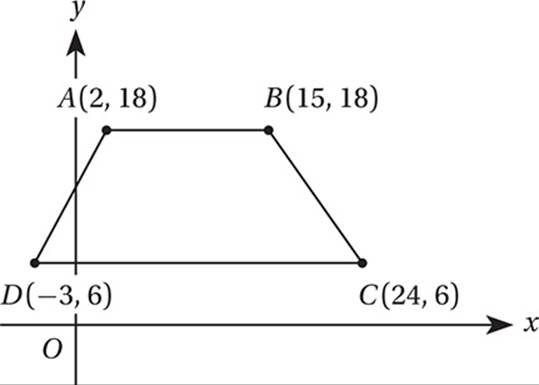
What is the area, in square units, of quadrilateral ABCD above?

(Medium) You might remember this figure from Lesson 4, in which we found its perimeter. Now we are asked to find its area. Unfortunately, we are not given any formula for calculating the area of this kind of quadrilateral. (You might remember that its technical name is a trapezoid, but in fact we don”t need to know anything special about trapezoids to solve this problem.) In such situations, it helps to remember the Strange Area Rule.
Strange Area Rule
When asked to find a “strange area,” that is, the area of a region for which you do not have a simple formula, try to analyze the region into the sum or the difference of simpler shapes.
In this case, we can look at this area in two different ways: as a rectangle plus two right triangles, or as a bigger rectangle minus two right triangles:
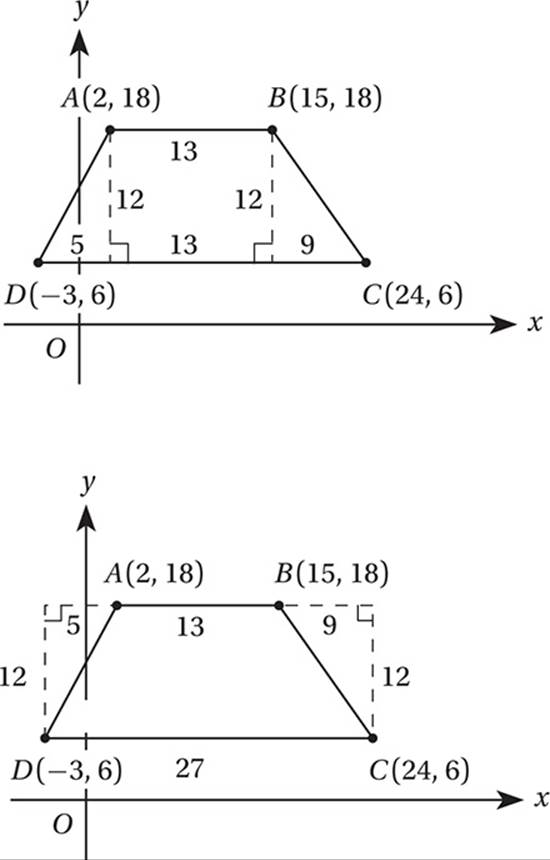
We should get the same result from either method. With the first method, the area of the trapezoid is the area of the rectangle plus the areas of two right triangles. This gives us a total area of (12)(13) + (1/2)(5)(12) + (1/2)(9)(12) = 156 + 30 + 54 = 240. With the second method, the area of the trapezoid is the area of the large rectangle minus the areas of the two right triangles. This gives us a total area of (12)(27) – (1/2)(5)(12) – (1/2)(9)(12) = 324 – 30 – 54 = 240. Bingo!
Lesson 8: Similar figures
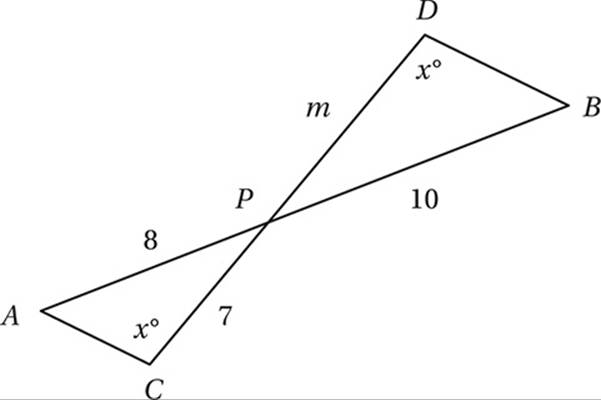
In the figure above, ![]() and
and ![]() are line segments that intersect at point P. What is the value of m?
are line segments that intersect at point P. What is the value of m?

(Medium) The key to this question is noticing that the two triangles are similar. That is, that they are the same shape, although they may be different sizes.
Similarity
In geometry, similar really just means the same shape. Two figures are similar if and only if all pairs of corresponding angles are congruent, and all pairs of corresponding sides are proportional.
Helpful Tip
Always be on the lookout for similar triangles in SAT Math diagrams!
AA (Angle-Angle) Similarity Theorem
If two triangles have two pairs of congruent corresponding angles, then (1) the remaining pair of corresponding angles must be congruent, and (2) the triangles must be similar.
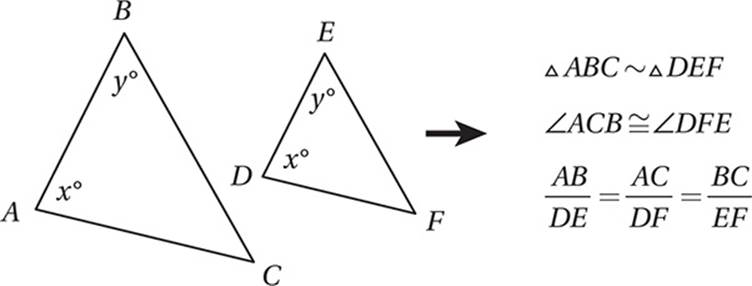
SAS (Side-Angle-Side) Similarity Theorem
If two triangles have two pairs of proportional corresponding sides, and the corresponding angles between those sides are also congruent, then the triangles must be similar.
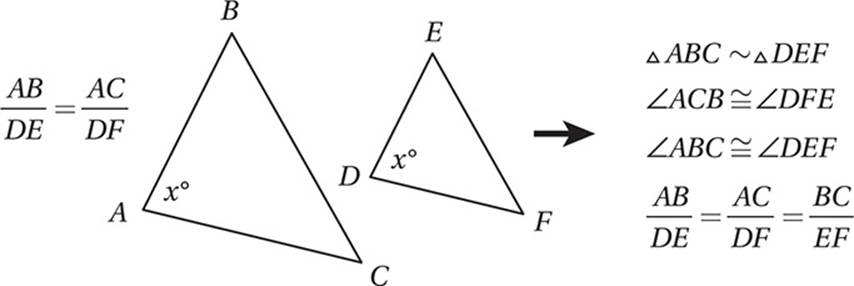
Perimeters, Areas, and Volumes of Similar Figures
If two polygons are similar with corresponding sides in ratio of a:b, then the corresponding perimeters of those figures have a ratio of a:b and their corresponding areas have a ratio of a2:b2. If two solids have corresponding lengths in a ratio of a:b, then their volumes have a ratio ofa3:b3.
Coming back to our diagram, if ![]() and
and ![]() intersect at point P, the Crossed Lines Theorem tells us that ∠ APC and ∠ BPD must be congruent, and so, by the AA Theorem, ΔAPC ∼ ΔBPD. Therefore, the corresponding sides are proportional:
intersect at point P, the Crossed Lines Theorem tells us that ∠ APC and ∠ BPD must be congruent, and so, by the AA Theorem, ΔAPC ∼ ΔBPD. Therefore, the corresponding sides are proportional:
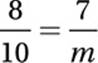
Cross multiply:
8m = 70
Divide by 8:
m = 70/8 = 8.75
Exercise Set 2: Geometry (No Calculator)
1
A cereal company sells oatmeal in two sizes of cylindrical containers. The radius of the larger container is twice that of the smaller, and the height of the larger container is 50% greater than the smaller. If the smaller container holds 10 ounces of oatmeal, how many ounces can the larger container hold?

2
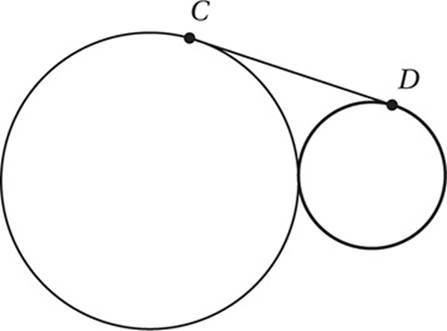
Note: Figure not drawn to scale.
In the figure above, ![]() is tangent to both circles, which are tangent to each other. If the smaller circle has a circumference of 4π and the larger circle has a circumference of 4π, what is the length of
is tangent to both circles, which are tangent to each other. If the smaller circle has a circumference of 4π and the larger circle has a circumference of 4π, what is the length of ![]() ?
?

3
What is the area, in square inches, of a circle with diameter 6π2 inches?
A) 9π4
B) 9π5
C) 36π4
D) 36π5
4
What is the length of the longest line segment that connects two vertices of a rectangular box that is 6 units wide, 4 units long, and 2 units tall?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
5
Which of the following equations represents a circle in the xy-plane that intersects the x-axis at (3, 0) and (9, 0)?
A) (x – 6)2 + (y – 4)2 = 25
B) (x – 3)2 + (y – 9)2 = 25
C) (x – 6)2 + (y – 4)2 = 36
D) (x – 3)2 + (y – 9)2 = 36
6
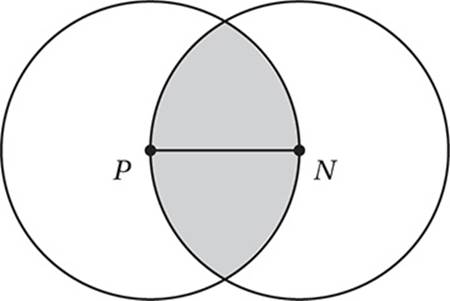
In the figure above, P and N are the centers of the circles and PN = 6. What is the area of the shaded region?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
7
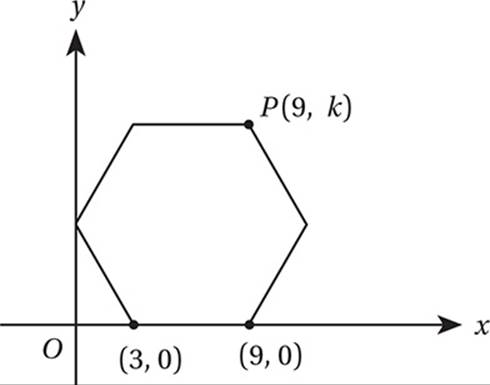
The diagram above shows a hexagon with all sides congruent and all angles congruent. What is the value of k?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Exercise Set 2: Geometry (Calculator)
8
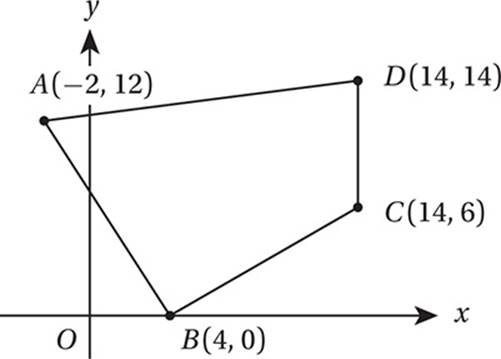
What is the area, in square units, of the quadrilateral above?

9
What is the degree measure, to the nearest whole degree, of an angle that measures 5.6 radians?

10
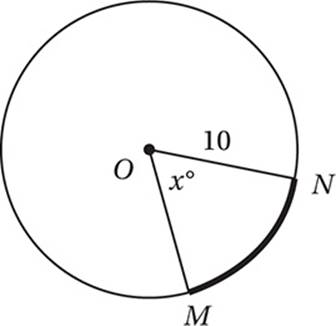
In the figure above, arc ![]() has a length of 11.5. To the nearest integer, what is the value of x?
has a length of 11.5. To the nearest integer, what is the value of x?

11
The Great Pyramid in Giza, Egypt, has a height of 140 meters and a volume of 2.6 million cubic meters. If a scale model of the Great Pyramid is to be built that is 2 meters high, what will be the volume, in cubic meters, of this model?

12
Which of the following equations defines a circle that is tangent to the y-axis?
A) (x – 2)2 + (y + 3)2 = 2
B) (x – 2)2 + (y + 3)2 = 3
C) (x – 2)2 + (y + 3)2 = 4
D) (x – 2)2 + (y + 3)2 = 9
![]()
Questions 13 and 14 refer to the diagram below.
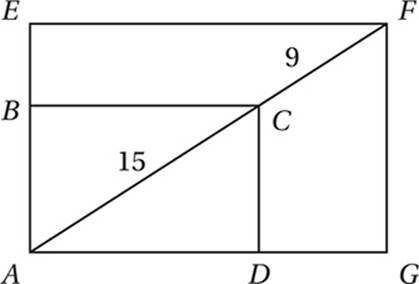
The figure above shows two rectangles that share a common vertex, and ![]() is a line segment that passes through C.
is a line segment that passes through C.
13
What is the ratio of the area of rectangle ABCD to the area of rectangle AEFG?
A) 3:5
B) 9:25
C) 5:8
D) 25:64
14
If CD = 9, what is the perimeter of rectangle AEFG?
A) 67.2
B) 72.6
C) 76.2
D) 78.6
![]()
15
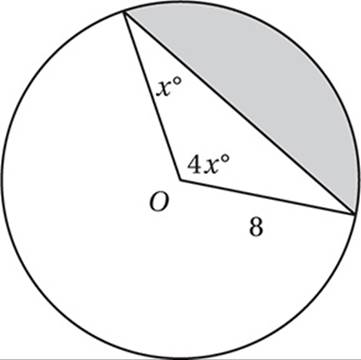
Point O is the center of the circle above. What is the area of the shaded region?
A) 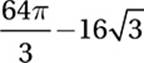
B) 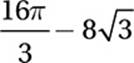
C) 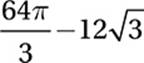
D) 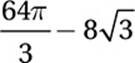
EXERCISE SET 2: GEOMETRY ANSWER KEY
No Calculator
1. 60 If the smaller cylinder has a radius of r and a height of h, its volume is πr2h. The larger cylinder therefore must have a radius of 2r and a height of 1.5h, and a volume of π(2r)2(1.5h) = 6πr2h. Since this is 6 times the volume of the smaller cylinder, it must hold 10 × 6 = 60 ounces of oatmeal.
2. 8 First, let”s draw the radii to the points of tangency, the segment joining the centers, and the segment from the center of the smaller circle that is perpendicular to the radius of the larger circle. Since the tangent segment is perpendicular to the radii, these segments form a rectangle and a right triangle.
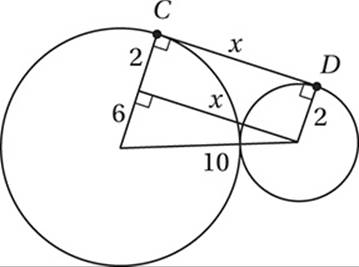
Since the circumference of the smaller circle is 4π, its radius is 2, and since the circumference of the larger circle is 16π, its radius is 8. The hypotenuse of the right triangle is the sum of the two radii: 2 + 8 = 10. One of the legs of the right triangle is the difference of the two radii: 8 – 2 = 6.
Pythagorean Theorem:
x2 + 62 = 102
Simplify:
x2 + 36 = 100
Subtract 36:
x2 = 64
Take square root:
x = 8
3. B Diameter = 2r:
2r = 6π2
Divide by 2:
r = 3π2
Area formula:
πr2 = π(3π2)2
Simplify:
πr2 = π(9π4)
Simplify:
πr2 = 9π5
4. C From the 3-D Distance Formula back in Lesson 4, the length of the diagonal is ![]()
![]()
5. A All of the equations are clearly equations of circles, so our only task is to verify that one of these equations is satisfied by both point (3, 0) and point (9, 0). Simply by plugging these coordinates into the equations, we can verify that only the equation in (A) is true for both points: (3 – 6)2 + (0 – 4)2 = 25 and (9 – 6)2 + (0 – 4)2 = 25.
6. C In this problem, we have to take advantage of the Strange Area Rule from Lesson 7. First we should draw the segments from P and N to the points of intersection. Since each of these segments is a radius, they have equal measure (6), and form two equilateral 60°-60 °60 ° triangles.
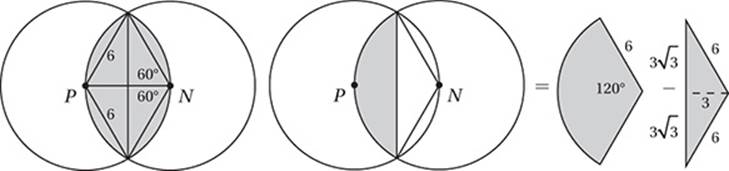
The shaded region is composed of two circle “segments,” each of which is a sector minus a triangle, as shown in the figure above. The sector, since it has a 120° central angle, has an area 1/3 of the whole circle, or (1/3) (π(6)2) = 12π and the triangle has area ![]() . Therefore, the shaded region has an area of
. Therefore, the shaded region has an area of ![]() .
.
7. B Each side of the hexagon has length 9 – 3 = 6. Each interior angle of a regular hexagon has measure (6 – 2)(180°)/6 = 120°, so the segments shown form two 30°-60°-90° triangles with lengths shown below.
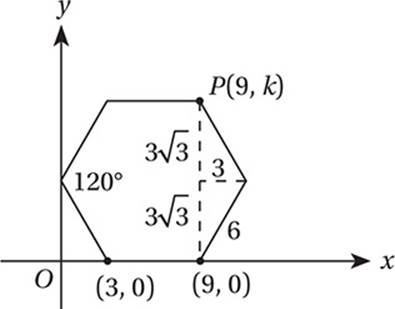
Therefore, ![]() .
.
Calculator
8. 142 First, let”s draw a rectangle around the figure as shown.
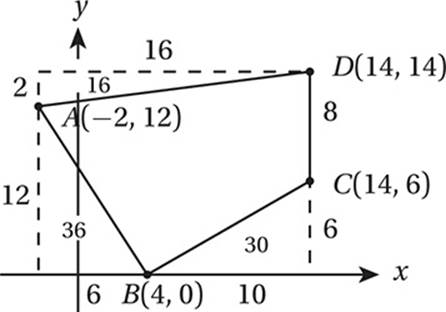
This shows that the area we want is the area of the rectangle minus the areas of the three triangles: (16)(14) – (1/2)(2)(16) – (1/2)(12)(6) – (1/2)(10)(6) = 224 – 16 – 36 – 30 = 142.
9. 321 To convert any angle from radians to degrees, we just multiply by the conversion factor (180°)/(π radians). 5.6 × 180°/π = 320.86 ≈ 321°.
10. 66 In a circle with radius 10, and arc of length 11.5 has a radian measure of 11.5/10 = 1.15 radians. In degrees, this equals 1.15 × 180°/π = 65.89° ≈ 66°.
11. 7.58 If two similar solids have sides in ratio of a:b, then their volumes are in a ratio of a3:b3. The ratio of the heights is 140:2 = 70:1, so the ratio of volumes is 703:13 = 343,000:1. This means that the volume of the model is 2,600,000 ÷343,000 ≈ 7.58 cubic meters.
12. C As a quick sketch will verify, in order for a circle to be tangent to the y-axis, its radius must equal the absolute value of the x-coordinate of its center. Since the center of each square is (2, –3), the radius must be 2. The only circle with a radius of 2 is (C).
13. D By the AA Theorem, triangle ACD is similar to triangle AFG, and so rectangle ABCD is similar to rectangle AEFG. The ratio of the corresponding sides is equal to the ratio of their diagonals, which is 15:24 = 5:8. Therefore, the ratio of their areas is 52:82 = 25:64
14. A If CD = 9, we can find AD by the Pythagorean Theorem. (AD)2 + (CD)2 = (AC)2
Substitute:
(AD)2 + 92 = 152
Simplify:
(AD)2 + 81 = 225
Subtract 81:
(AD)2 = 144
Take square root:
AD = 12
This means that the perimeter of ABCD is 12 + 9 + 12 + 9 = 42. Since the ratio of the perimeters of similar figures equals the ratio of corresponding sides,
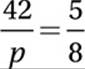
Cross multiply:
5p = 336
Divide by 5:
p = 67.2
15. A The two radii and the chord form an isosceles triangle.
x + x + 4x = 180
Simplify:
6x = 180
Divide by 6:
x = 30
Therefore, the diagram should look like this:
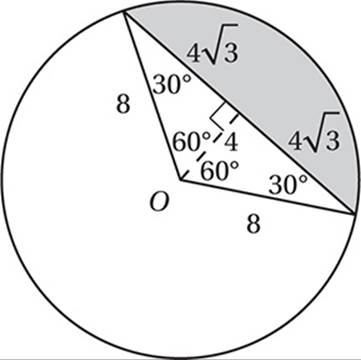
As we saw in question 6, this portion of the circle is called a “segment,” and we find its area by taking the area of the sector minus the area of the triangle. The sector has area (120/360)(π82) = 64π/3, and the triangle has area ![]() , so the segment has an area of
, so the segment has an area of ![]() .
.