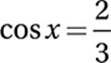SAT 2016
CHAPTER 10
THE SAT MATH: ADDITIONAL TOPICS
Skill 2: Understanding Basic Trigonometry
Lesson 9: The basic trigonometric functions
Which of these is equivalent to 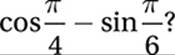 ? (No calculator)
? (No calculator)
A) 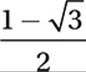
B) 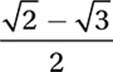
C) 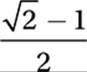
D) 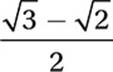
The Basic Trigonometric Functions
Any of the three basic trigonometric functions, like all functions, takes an input number and transforms it into an output number. A trigonometric function takes an angle, θ, as an input and constructs a right triangle with θ as one of its acute angles. The output is then the ratio of two sides of that triangle as defined by the mnemonic SOH-CAH-TOA.
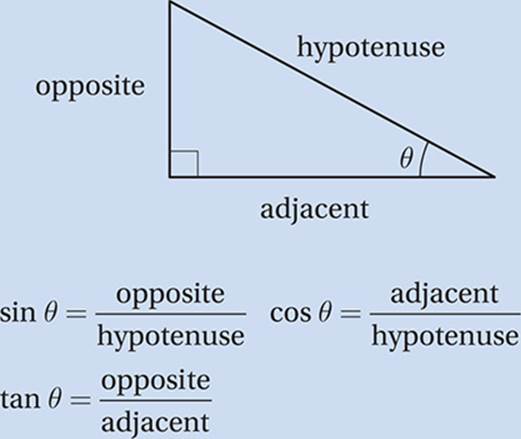
But these definitions are limited, because they only work when θ is an acute angle. What if it”s a larger angle, like 135°, or even a negative angle, like –20°? To find the trigonometric ratios for these angles, we use the unit circle.
The Unit Circle
The unit circle is just a circle with radius 1 centered at the origin of the xy-plane. When using the unit circle, all angles must be in standard position, that is, with vertex at the origin and measured counterclockwise from the positive x-axis (just like the angle θ in the following figure).
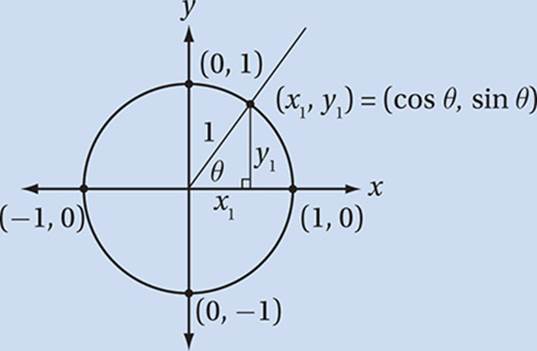
When an angle, θ, is in standard position, its terminal ray intersects the unit circle in the point (x1, y1). If we drop a vertical line segment from this point to the x-axis, we form a right triangle with legs of length x1 and y1 and a hypotenuse of length 1 (as shown above).
So now let”s go back to the definitions of the basic trigonometric functions. In terms of this right triangle, what are the sine, cosine, and tangent of θ?

This suggests three important theorems:
• The sine of any angle is the y-coordinate of its corresponding point on the unit circle.
• The cosine of any angle is the x-coordinate of its corresponding point on the unit circle.
• The tangent of any angle is the ratio of the y-coordinate to the x-coordinate of its corresponding point on the unit circle.
(Medium-hard) First, you may find it useful to convert the angles to degree measures using the conversion factor (180°/π radians). This gives us π/4 radians = 45° and π/6 radians = 30°. We should recognize these as angles in two Special Right Triangles:
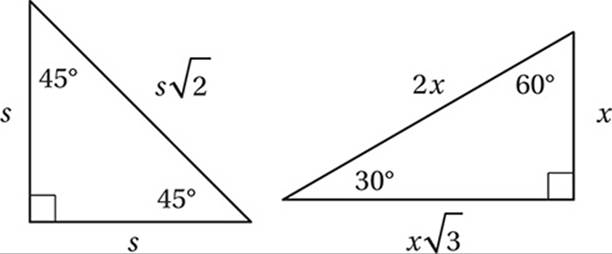
Using the definitions for sine and cosine above, these triangles show us that 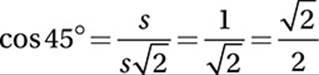 and
and 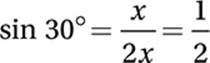 . Therefore,
. Therefore, 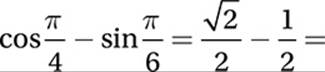
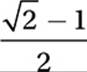 and the correct answer is (C).
and the correct answer is (C).
If sin x = a and sin z = −a, where x and z are in radians, and 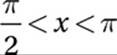 , which of the following could be the value of z in terms of x?
, which of the following could be the value of z in terms of x?
A) π – x
B) x – π
C) 2π + x
D) 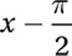
(Hard) The statement 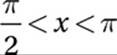 indicates that x is an angle in quadrant II, where the sine (the y-value of the points on the unit circle) is positive. Let”s draw this situation on the unit circle so we can visualize it. (We don”t want to confuse the angles called x and y in the problem with thex-coordinates and y-coordinates in the xy-plane. For this reason, let”s label the terminal rays for the angles “angle x” and “angle z.”) Recall that the sine of any angle is the y-coordinate of the point on the unit circle that corresponds to that angle. If sin x = a, then a is the y-coordinate of the point on the unit circle that corresponds to “angle x,” as shown in the diagram. If sin z = –a, then –a is the y-coordinate of the point on the unit circle that corresponds to “angle z.” There are two possible locations for “angle z” as shown in the diagram.
indicates that x is an angle in quadrant II, where the sine (the y-value of the points on the unit circle) is positive. Let”s draw this situation on the unit circle so we can visualize it. (We don”t want to confuse the angles called x and y in the problem with thex-coordinates and y-coordinates in the xy-plane. For this reason, let”s label the terminal rays for the angles “angle x” and “angle z.”) Recall that the sine of any angle is the y-coordinate of the point on the unit circle that corresponds to that angle. If sin x = a, then a is the y-coordinate of the point on the unit circle that corresponds to “angle x,” as shown in the diagram. If sin z = –a, then –a is the y-coordinate of the point on the unit circle that corresponds to “angle z.” There are two possible locations for “angle z” as shown in the diagram.
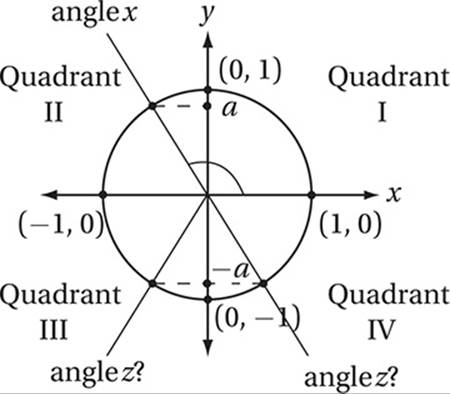
At this point, it may be easiest to simply pick a value for “angle x” that is between π/2 (≈ 1.57) and π (≈ 3.14), such as x = 2. Since sin 2 ≈ 0.909 (remember to put your calculator into “radian mode”), a = 0.909. Now we just need to find which angle among the choices has a sine of − 0.909
A) sin(π –2) = 0.0909
B) sin(2 – π) = –0.909
C) sin(2π + π) = 0.0909
D) sin(2 – π/2) = 0.416
Therefore, the correct answer is (B).
The Pythagorean Identity
sin2 x + cos2 x = 1 for all values of x
An identity is an algebraic equation that is true for all values of the unknown, and not just for particular values. We can prove the Pythagorean Identity by just applying the Pythagorean Theorem to our right triangle and thinking about the trigonometric ratios.
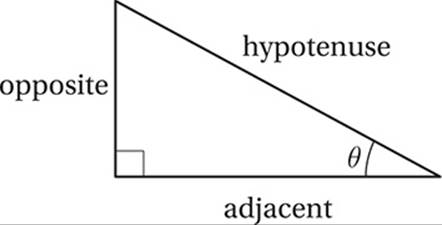
Apply Pythagorean Theorem:
(opposite)2 + (adjacent)2 = (hypotenuse)2
Divide by (hypotenuse)2:

Simplify using trig definitions:
sin2 θ + cos2 θ = 1
If b is an angle measure such that sin 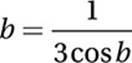 , what is the value of (sin b – cos b)2?
, what is the value of (sin b – cos b)2?
A) ![]()
B) ![]()
C) 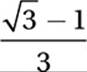
D) 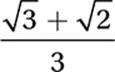
(Medium) The expression we are trying to evaluate includes squared trigonometric ratios, so we will probably have to take advantage of the Pythagorean Identity.
Expression to evaluate:
(sin b – cos b)2
FOIL:
sin2 b – 2sin b cos b + cos2 b
Rearrange using Commutative Law of Addition:
sin2 b + cos2 b – 2sin b cos b
Substitute sin2 b + cos2 b = 1:
1 – 2sin b cos b
Now we”ll have to find the value of sin b cos b, which we can find with the given equation.
Given equation:
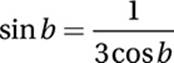
Multiply by cos b:
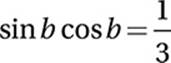
Substitute sin b cos b =![]()
into original expression:
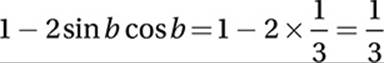
So the correct answer is (A).
Lesson 10: The trigonometry of complementary angles
If sin 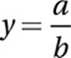 and
and 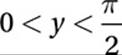 , which of the following is equal to sin
, which of the following is equal to sin 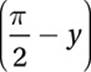 ?
?
A) 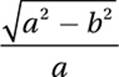
B) 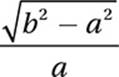
C) 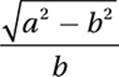
D) 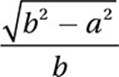
Trigonometry of Complementary Angles
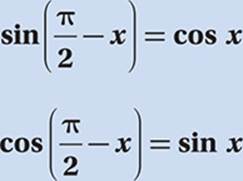
The two acute angles in a right triangle are complements of one another, that is, they have a sum of 90° (or, in radians, ![]() ). So, if one of the angles has a radian measure of x, the other has a measure of
). So, if one of the angles has a radian measure of x, the other has a measure of ![]() – x.
– x.
If we look at the trigonometric ratios for this new angle, we see that these ratios are related to the trigonometric ratios of its complement by the following rule: The trigonometric ratio of any angle equals the cofunction of its complement.
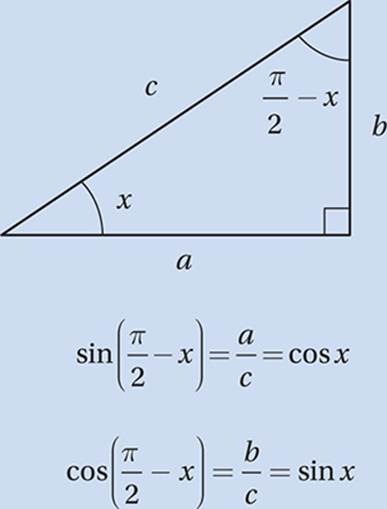
(Medium-hard) Let”s start by drawing a picture of this situation. Since y is the measure of an acute angle, we can imagine it as the interior angle of a right triangle. Since its sine is equal to a/b, we can say that the opposite side has measure a and the hypotenuse has measure b.
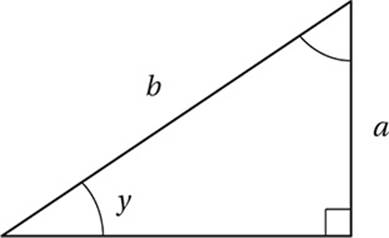
Now we can find the length of the remaining leg (let”s call it k) in terms of a and b using the Pythagorean
Theorem:
k2 + a2 = b2
Subtract a2:
k2 = b2 – a2
Take the square root:
![]()
Also, we know that the other acute angle has a measure of ![]() –y, so let”s complete the picture:
–y, so let”s complete the picture:
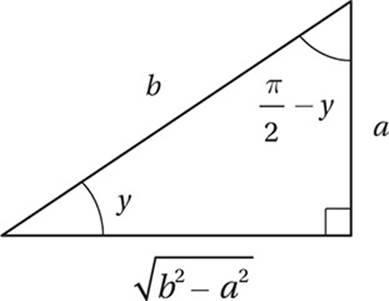
Now, finding the value of 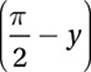 is just a matter of using the definition of sine: SOH.
is just a matter of using the definition of sine: SOH.
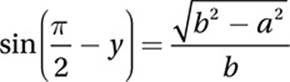
So the correct answer is (D).
Exercise Set 3: Trigonometry (No Calculator)
1
What is the greatest possible value of f if 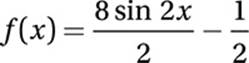 ?
?

2
If 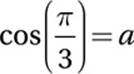 , what is the value of
, what is the value of 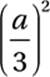 ?
?

3
If (sin x – cos x)2 = 0.83, what is the value of (sin x + cos x)2?

4
Which of the following is equivalent to 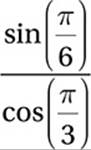 ?
?
A) ![]()
B) ![]()
C) ![]()
D) 1
5
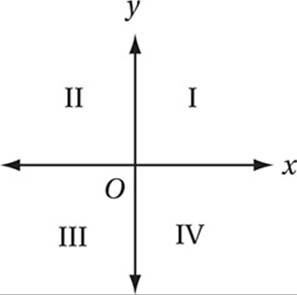
If sin >θ < 0 and sin θ cos θ < 0, then θ must be in which quadrant of the figure above?
A) I
B) II
C) III
D) IV
6
If 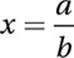 and
and 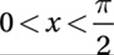 , which of the following expressions is equal to
, which of the following expressions is equal to ![]() ?
?
A) 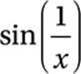
B) 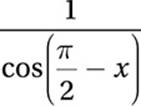
C) 1 − sin2x
D) 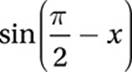
7
If sin b = a, which of the following could be the value of cos (b + π)?
A) ![]()
B) a2
C) ![]()
D) 1 – a2
8
If 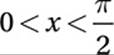 and
and 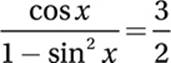 , what is the value of cos x?
, what is the value of cos x?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
EXERCISE SET 3: TRIGONOMETRY ANSWER KEY
No Calculator
1. 7/2 or 3.5 The discussion in Lesson 9 about the definition of the sine function and the unit circle made it clear that the value of the sine function ranges from –1 to 1. Therefore, the maximum value of 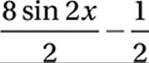 is
is 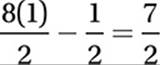 or 3.5.
or 3.5.
2. 1/36 or .027 or .028 An radian measure of π/3 is equivalent to 60 °. If you haven”t memorized the fact that cos(60 °) = ½, you can derive it from the Reference Information at the beginning of every SAT Math section, which includes the 30°-60°-90° special right triangle. Since a = ½, (a/3)2 = (1/6)2 = 1/36.
3. 1.17
(sin x – cos x)2 = 0.83
FOIL:
sin2 x – 2sin x cos x + cos2 x = 0.83
Regroup:
sin2 x + cos2 x – 2sin x cos x = 0.83
Simplify:
1 – 2sin x cos x = 0.83
Subtract 1:
–2sin x cos x = –0.17
Multiply by –1:
2sin x cos x = 0.17
Evaluate this expression:
(sin x + cos x)2
FOIL:
sin2 x + 2sin x cos x + cos2 x
Regroup:
sin2 x + cos2 x + 2sin x cos x
Substitute:
1 + 0.17 = 1.17
4. D sin(π/6) = ½ and cos(π/3) = ½, so sin(π/6)/cos(π/3) = 1.
5. D If sin θ < 0, then θ must be either in quadrant III or in quadrant IV. (Remember that sine corresponds to the y-coordinates on the unit circle, so it is negative in those quadrants where the y-coordinates are negative.) If sin θ cos θ < 0, then cos θ must be positive (because a negative times a positive is a negative). Since cos θ is only positive in quadrants I and IV (because cosine corresponds to the x-coordinates on the unit circle), θ must be in quadrant IV
6. B First, notice that a/b and b/a are reciprocals. Next, we can use the identity in Lesson 10 that 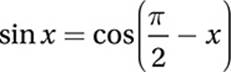 to see that choice (B) is just the reciprocal of sin x. Alternately, we can just choose a value of x, like x = 1, and evaluate sin 1 = 0.841. The correct answer is the expression that gives a value equal to the reciprocal of 0.841, which is 1/0.841 = 1.19. Plugging in x = 1 gives (A) 0.841, (B) 1.19, (C) 0.292, (D) 0.540.
to see that choice (B) is just the reciprocal of sin x. Alternately, we can just choose a value of x, like x = 1, and evaluate sin 1 = 0.841. The correct answer is the expression that gives a value equal to the reciprocal of 0.841, which is 1/0.841 = 1.19. Plugging in x = 1 gives (A) 0.841, (B) 1.19, (C) 0.292, (D) 0.540.
7. C Recall from the Pythagorean Identity that cos ![]() . Substituting sin b = a gives cos
. Substituting sin b = a gives cos ![]() . The angle b + π is the reflection of angle b through the origin, so cos(b + π) is the opposite of cos b, which means that cos
. The angle b + π is the reflection of angle b through the origin, so cos(b + π) is the opposite of cos b, which means that cos ![]() .
.
8. D Recall from the Pythagorean Identity that cos2 x = 1 − sin2 x
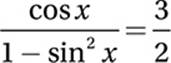
Substitute cos2 x = 1 – sin2 x:
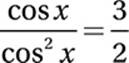
Cancel common factor:
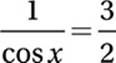
Reciprocate: