CONCEPTS IN BIOLOGY

PART IV. EVOLUTION AND ECOLOGY

15. Ecosystem Dynamics. The Flow of Energy and Matter

15.3. Energy Flow Through Ecosystems

The ancient Egyptians constructed elaborate tombs we call pyramids. The broad base of the pyramid is necessary to support the upper levels of the structure, which narrows to a point at the top. The same kind of relationship exists for the various trophic levels of ecosystems. Biologists have adopted this pyramid model as a way to think about how ecosystems are organized. Most ecosystems have large quantities of producers, small quantities of herbivores, and still smaller quantities of carnivores. Because this is so common, ecologists have sought reasons to explain the relationship.

Laws of Thermodynamics

Two fundamental physical laws of energy are important when looking at ecological systems from an energy point of view. The first law of thermodynamics states that energy is neither created nor destroyed. That means that we should be able to describe the amounts of energy in each trophic level and follow energy as it flows through successive trophic levels. The second law of thermodynamics states that, when energy is converted from one form to another, some energy escapes to the surroundings as heat. This means that, as energy passes from one trophic level to the next, there is a reduction in the amount of energy in living things and an increase in the amount of heat in their surroundings (figure 15.4).

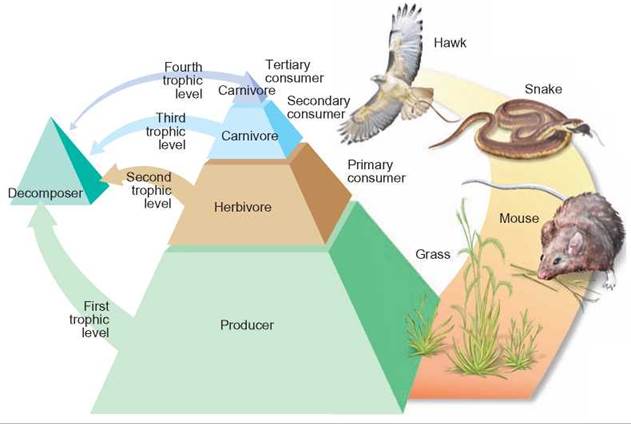
FIGURE 15.4. Energy and Trophic Levels

The producer trophic level has the greatest amount of energy and matter. At each successive trophic level, there is less energy and matter.

Think of any energy-converting machine; a certain amount of energy enters the machine and a certain amount of work is done. However, it also releases a great deal of heat energy. For example, an automobile engine must have a cooling system to get rid of the heat energy produced. Similarly, electrical energy is used in an incandescent lightbulb to produce light, but the bulb also produces large amounts of heat. Although living systems are somewhat different, they follow the same energy rules.

The Pyramid of Energy

The energy within an ecosystem can be measured in several ways. One simple way is to collect all the organisms present at any trophic level and burn them. For example, all the plants in a small field (producer trophic level) can be harvested and burned. The number of calories of heat produced by burning is equivalent to the energy content of the organic material collected. Similarly, all the herbivores in the second trophic level could be collected and burned. Then you could compare the amount of heat generated by producers and herbivores and get an idea of how much energy is lost as you go from the producer to the herbivore trophic level.

Another way of determining the energy present is to measure the rate of photosynthesis and respiration of a group of producers. The difference between the rates of respiration and photosynthesis is the amount of energy trapped in the living material of the plants.

When we examine a wide variety of ecosystems, we find that the producer trophic level has the most energy, the herbivore trophic level has less, and the carnivore trophic level has the least. In general, there is about a 90% loss of energy from one trophic level to the next higher level. Actual measurements vary from one ecosystem to another. Some may lose as much as 99%, whereas other, more efficient systems may lose only 70%, but 90% is a good rule of thumb. This loss in energy content at the second and subsequent trophic levels is primarily due to the second law of thermodynamics. (Whenever energy is converted from one form to another, some energy is lost to the surroundings as heat.)

In addition to the loss of energy as a result of the second law of thermodynamics, there is an additional loss involved in the capture and processing of food material by herbivores and carnivores. Although herbivores don’t need to chase their food, they do need to travel to where food is available, then gather, chew, digest, and metabolize it (figure 15.5). All of these processes require energy. Just as the herbivore trophic level experiences a 90% loss in energy content, the higher trophic levels of primary carnivores, secondary carnivores, and tertiary carnivores also experience a 90% reduction in the energy available to them. Figure 15.6 shows the flow of energy through an ecosystem.

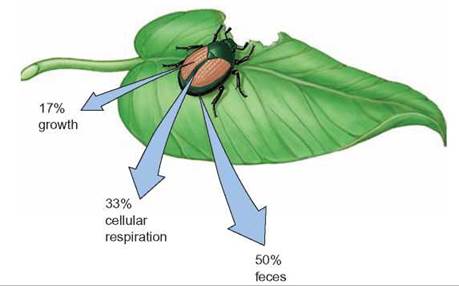
FIGURE 15.5. Energy Losses in an Herbivore

When an insect eats a plant to obtain energy, only a small amount is actually converted to new biological tissue in the insect.

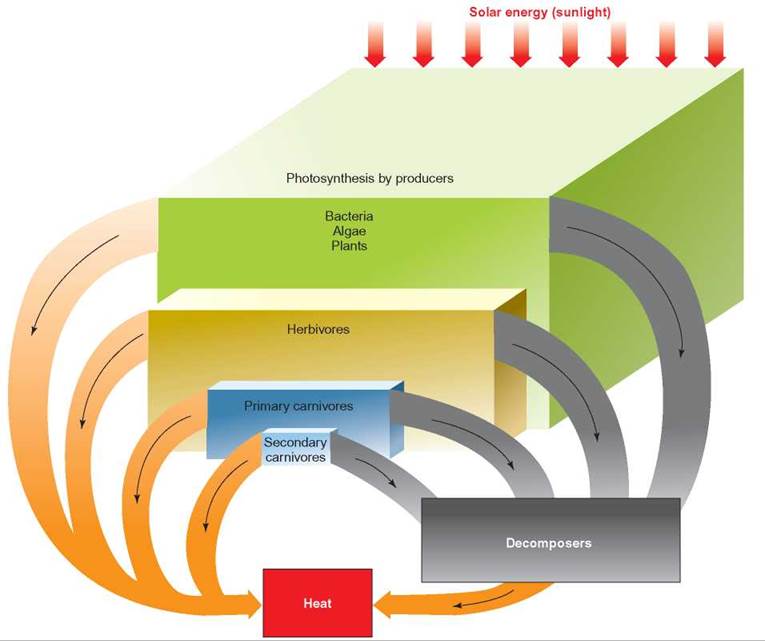
FIGURE 15.6. Energy Flow Through an Ecosystem

Energy from the Sun is captured by organisms that carry on photosynthesis. These are the producers at the first trophic level. As energy flows from one trophic level to the next, approximately 90% of it is lost. This means that the amount of energy at the producer level must be 10 times larger than the amount of energy at the herbivore level. Ultimately, all the energy used by organisms is released to the surroundings as heat.

The Pyramid of Numbers

Because it is difficult to measure the amount of energy at any one trophic level of an ecosystem, scientists often use other methods to quantify trophic levels. One method is simply to count the number of organisms at each trophic level. This generally gives the same pyramid relationship, called a pyramid of numbers (figure 15.7). This is not a very good method to use if the organisms at the different trophic levels are of greatly differing sizes. For example, if you counted all the small insects feeding on the leaves of one large tree, you would actually get an inverted pyramid.

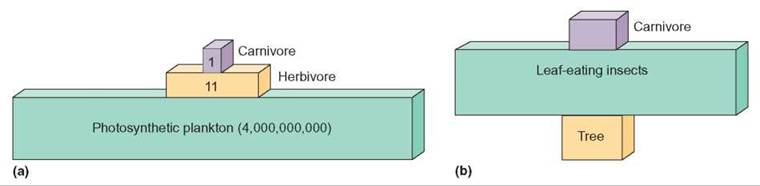
FIGURE 15.7. Pyramid of Numbers

One of the easiest ways to quantify the various trophic levels in an ecosystem is to count the number of individuals in a small portion of the ecosystem. As long as all the organisms are of similar size and live about the same length of time, this method gives a good picture of how the trophic levels are related. (a) The relationship among photosynthetic plankton in the ocean, the herbivores that eat them, and the carnivores that eat the herbivores is a good example. However, if the organisms at one trophic level are much larger or live much longer than those at other levels, the picture of the relationship may be distorted. (b) This is the relationship between forest trees and the insects that feed on them. This pyramid of numbers is inverted.

The Pyramid of Biomass

One way to overcome some of the problems associated with simply counting organisms is to measure the biomass at each trophic level. Biomass is the amount of living material present; it is usually determined by collecting all the organisms at one trophic level and measuring their dry weight. This eliminates the size-difference problem associated with a pyramid of numbers, because all the organisms at each trophic level are combined and weighed. The pyramid of biomass also shows the typical 90% loss at each trophic level.

Although a pyramid of biomass is better than a pyramid of numbers in measuring some ecosystems, it has some shortcomings. Some organisms tend to accumulate biomass over long periods of time, whereas others do not. Many trees live for hundreds of years; their primary consumers, insects, generally live only 1 year. Likewise, a whale is a long-lived animal, whereas its food organisms are relatively short-lived. Figure 15.8 shows two pyramids of biomass.

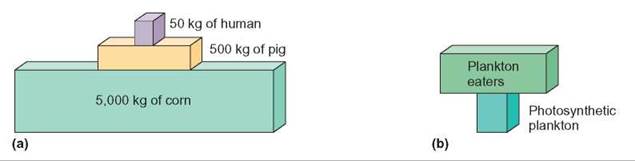
FIGURE 15.8. Pyramid of Biomass

Biomass is determined by collecting and weighing all the organisms in a small portion of an ecosystem. (a) This method of quantifying trophic levels eliminates the problem of different-sized organisms at different trophic levels. However, it does not always give a clear picture of the relationship among trophic levels if the organisms have widely different lengths of life. (b) For example, in aquatic ecosystems, many of the small producers divide several times per day. The tiny animals (zooplankton) that feed on them live much longer and tend to accumulate biomass over time. The single-celled algae produce much more living material but are eaten as fast as they are produced and, so, do not accumulate a large biomass.

15.3. CONCEPT REVIEW

7. What is the second law of thermodynamics? Why is it important for understanding energy relationships in ecosystems?

8. Why is the biomass of the herbivore trophic level larger than the biomass of the carnivore trophic level?

9. List an advantage and a disdvantage to using each of the following for characterizing relationships among organisms in an ecosystem: pyramid of energy, pyramid of biomass, and pyramid of numbers.