Medical Microbiology

Section 1 The adversaries – microbes

2 The bacteria

Introduction

Although free-living bacteria exist in huge numbers, relatively few species cause disease. The majority of these are well known and well studied; however, new pathogens continue to emerge and the significance of previously unrecognized infections becomes apparent. Good examples of the latter include infection with Legionella, the cause of Legionnaires’ disease, coronavirus-associated severe acute respiratory syndrome (SARS), and gastric ulcers associated with Helicobacter pylori infection.

Bacteria are single-celled prokaryotes, their DNA forming a long circular molecule, but not contained within a defined nucleus. Many are motile, using a unique pattern of flagella. The bacterial cell is surrounded by a complex cell wall and often a thick capsule. They reproduce by binary fission, often at very high rates, and show a wide range of metabolic patterns, both aerobic and anaerobic. Classification of bacteria uses both phenotypic and genotypic data. For clinical purposes, the phenotypic data are of most practical value, and rest on an understanding of bacterial structure and biology (see Fig. 32.15). Detailed summaries of members of the major bacterial groups are given in the Pathogen Parade (see online appendix).

Structure

Bacteria are ‘prokaryotes’ and have a characteristic cellular organization

The genetic information of bacteria is carried in a long, double-stranded (ds), circular molecule of DNA (Fig. 2.1). By analogy with eukaryotes (see Ch. 1), this can be termed a ‘chromosome’, but there are no introns; instead, the DNA comprises a continuous coding sequence of genes. The chromosome is not localized within a distinct nucleus; no nuclear membrane is present and the DNA is tightly coiled into a region known as the ‘nucleoid’. Genetic information in the cell may also be extrachromosomal, present as small circular self-replicating DNA molecules termed plasmids. The cytoplasm contains no organelles other than ribosomes for protein synthesis. Although ribosomal function is the same in both pro- and eukaryotic cells, organelle structure is different. Ribosomes are characterized as 70 S in prokaryotes and 80 S in eukaryotes (the ‘S’ unit relates to how a particle behaves when studied under extreme centrifugal force in an ultracentrifuge). The bacterial 70 S ribosome is specifically targeted by antimicrobials such as the aminoglycosides (see Ch. 33). Many of the metabolic functions performed in eukaryote cells by membrane-bound organelles such as mitochondria are carried out by the prokaryotic cell membrane. In all bacteria except mycoplasmas, the cell is surrounded by a complex cell wall. External to this wall may be capsules, flagella and pili. Knowledge of the cell wall and these external structures is important in diagnosis and pathogenicity and for understanding bacterial biology.

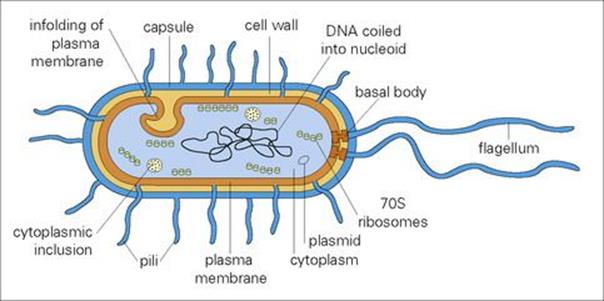
Figure 2.1 Diagrammatic structure of a generalized bacterium.

Bacteria are classified according to their cell wall as Gram-positive or Gram-negative

Gram staining is a basic microbiologic procedure for detection and identification of bacteria (see Ch. 32). The main structural component of the cell wall is a ‘peptidoglycan’ (mucopeptide or murein), a mixed polymer of hexose sugars (N-acetylglucosamine and N-acetylmuramic acid) and amino acids.

• In Gram-positive bacteria, the peptidoglycan forms a thick (20–80 nm) layer external to the cell membrane, and may contain other macromolecules.

• In Gram-negative species, the peptidoglycan layer is thin (5–10 nm) and is overlaid by an outer membrane, anchored to lipoprotein molecules in the peptidoglycan layer. The principal molecules of the outer membrane are lipopolysaccharides and lipoprotein (Fig. 2.2).

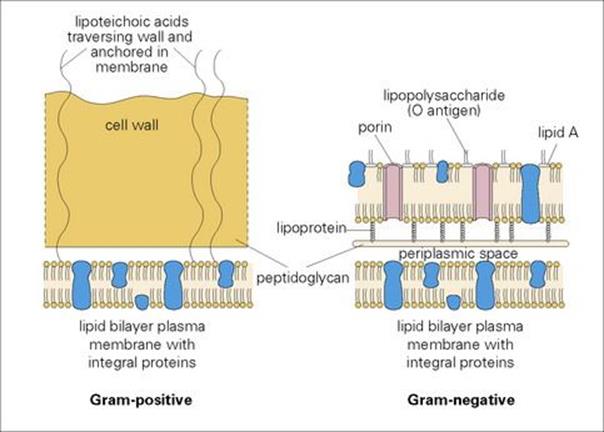
Figure 2.2 Construction of the cell walls of Gram-positive and Gram-negative bacteria.

The polysaccharides and charged amino acids in the peptidoglycan layer make it highly polar, providing the bacterium with a thick hydrophilic surface. This property allows Gram-positive organisms to resist the activity of bile in the intestine. Conversely, the layer is digested by lysozyme, an enzyme present in body secretions, which therefore has bactericidal properties. Synthesis of peptidoglycan is disrupted by beta-lactam and glycopeptides antibiotics (see Ch. 33).

In Gram-negative bacteria, the outer membrane is also hydrophilic, but the lipid components of the constituent molecules give hydrophobic properties as well. Entry of hydrophilic molecules such as sugars and amino acids is necessary for nutrition and is achieved through special channels or pores formed by proteins called ‘porins’. The lipopolysaccharide (LPS) in the membrane confers both antigenic properties (the ‘O antigens’ from the carbohydrate chains) and toxic properties (the ‘endotoxin’ from the lipid A component; see Ch. 17).

In the Gram-positive mycobacteria, the peptidoglycan layer has a different chemical basis for cross-linking to the lipoprotein layer, and the outer envelope contains a variety of complex lipids (mycolic acids). These create a waxy layer, which both alters the staining properties of these organisms (the so-called acid-fast bacteria) and gives considerable resistance to drying and other environmental factors. Mycobacterial cell wall components also have a pronounced adjuvant activity (i.e. they promote immunologic responsiveness).

External to the cell wall may be an additional capsule of high molecular weight polysaccharides (or amino acids in anthrax bacilli) that gives a slimy surface. This provides protection against phagocytosis by host cells and is important in determining virulence. With Streptococcus pneumoniae infection, only a few capsulated organisms can cause a fatal infection, but unencapsulated mutants cause no disease.

The cell wall is a major contributor to the ultimate shape of the organism, an important characteristic for bacterial identification. In general, bacterial shapes (Fig. 2.3) are categorized as either spherical (cocci), rods (bacilli) or helical (spirilla), although there are variations on these themes.

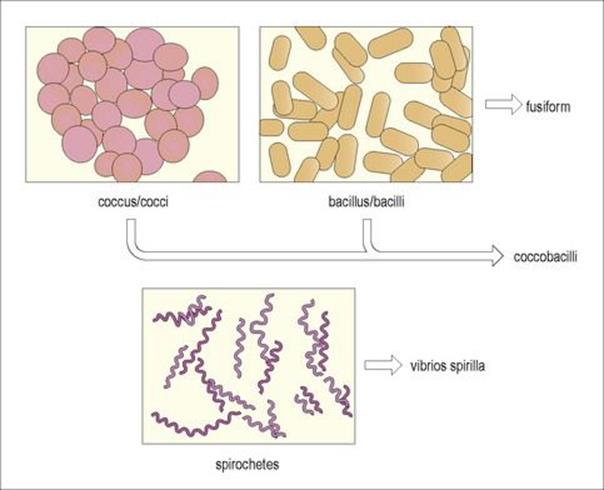
Figure 2.3 The three basic shapes of bacterial cells.

Many bacteria possess flagella

Flagella are long helical filaments extending from the cell surface, which enable bacteria to move in their environment. These may be restricted to the poles of the cell, singly (polar) or in tufts (lophotrichous), or distributed over the general surface of the cell (peritrichous). Bacterial flagella are quite different from eukaryote flagella, and the forces that result in movement are generated quite differently (being independent of adenosine triphosphate (ATP)). Motility allows positive and negative responses to chemical stimuli (chemotaxis). Flagella are built of protein components (flagellins), which are strongly antigenic. These antigens, the H antigens, are important targets of protective antibody responses.

Pili are another form of bacterial surface projection

Pili (fimbriae) are more rigid than flagella and function in attachment, either to other bacteria (the ‘sex’ pili) or to host cells (the ‘common’ pili). Adherence to host cells involves specific interactions between component molecules of the pili (adhesins) and molecules in host cell membranes. For example, the adhesins of Escherichia coli interact with fucose/mannose molecules on the surface of intestinal epithelial cells (see Ch. 22). The presence of many pili may help to prevent phagocytosis, reducing host resistance to bacterial infection. Although immunogenic, their antigens can be changed, allowing the bacteria to avoid immune recognition. The mechanism of ‘antigenic variation’ has been elucidated in the gonococci and is known to involve recombination of genes coding for ‘constant’ and ‘variable’ regions of pili molecules.

Nutrition

Bacteria obtain nutrients mainly by taking up small molecules across the cell wall

Bacteria take up small molecules such as amino acids, oligosaccharides and small peptides across the cell wall. Gram-negative species can also take up and use larger molecules after preliminary digestion in the periplasmic space. Uptake and transport of nutrients into the cytoplasm is achieved by the cell membrane using a variety of transport mechanisms, including facilitated diffusion which utilizes a carrier to move compounds to equalize their intra- and extracellular concentrations, and active transport where energy is expended to deliberately increase intracellular concentrations of a substrate. Oxidative metabolism (see below) also takes place at the membrane–cytoplasm interface.

Some species require only minimal nutrients in their environment, having considerable synthetic powers, whereas others have complex nutritional requirements. E. coli, for example, can be grown in media providing only glucose and inorganic salts; streptococci, on the other hand, will grow only in complex media providing them with many organic compounds. Nevertheless, all bacteria have similar general nutritional requirements for growth which are summarized in Table 2.1.

Table 2.1 Major nutritional requirements for bacterial growth

All pathogenic bacteria are heterotrophic

All bacteria obtain energy by oxidizing preformed organic molecules (carbohydrates, lipids and proteins) from their environment. Metabolism of these molecules yields ATP as an energy source. Metabolism may be aerobic, where the final electron acceptor is oxygen, or anaerobic, where the final acceptor may be an organic or inorganic molecule other than oxygen.

• In aerobic metabolism (i.e. aerobic respiration), complete utilization of an energy source such as glucose produces 38 molecules of ATP.

• Anaerobic metabolism utilizing an inorganic molecule other than oxygen as the final hydrogen acceptor (anaerobic respiration) is incomplete and produces fewer ATP molecules than aerobic respiration.

• Anaerobic metabolism utilizing an organic final hydrogen acceptor (fermentation) is much less efficient and produces only two molecules of ATP.

Anaerobic metabolism, while less efficient, can thus be used in the absence of oxygen when appropriate substrates are available, as they usually are in the host’s body. The requirement for oxygen in respiration may be ‘obligate’ or it may be ‘facultative’, some organisms being able to switch between aerobic and anaerobic metabolism. Those that use fermentation pathways often use the major product pyruvate in secondary fermentations by which additional energy can be generated. The interrelationship between these different metabolic pathways is illustrated in Figure 2.4.

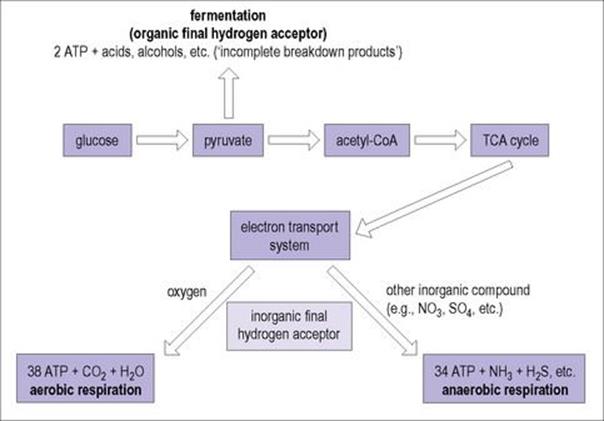
Figure 2.4 Catabolic breakdown of glucose in relationship to final hydrogen acceptor.

The ability of bacteria to grow in the presence of atmospheric oxygen relates to their ability to enzymatically deal with potentially destructive intracellular reactive oxygen species (e.g. free radicals, anions containing oxygen, etc.) (Table 2.2). The interaction between these harmful compounds and detoxifying enzymes such as superoxide dismutase, peroxidase, and catalase is illustrated in Figure 2.5 (also see Ch. 9 and Box 9.2).

Table 2.2 Bacterial classification in response to environmental oxygen

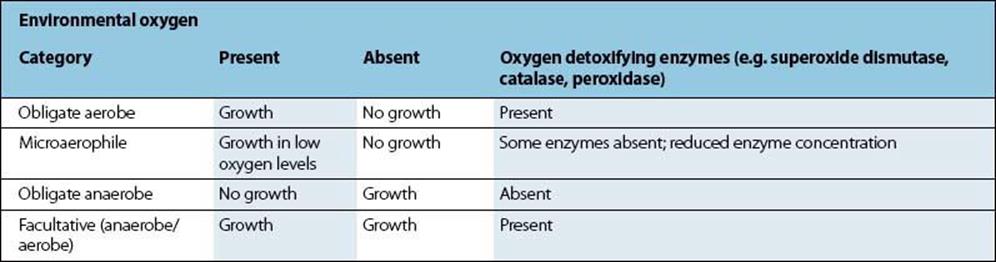
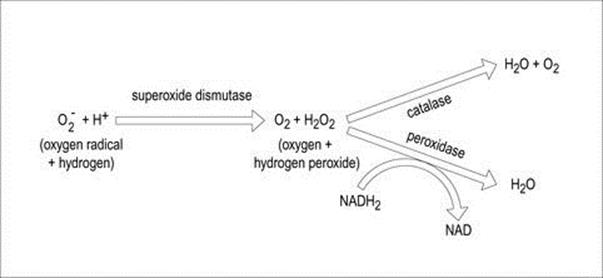
Figure 2.5 Interaction between oxygen detoxifying enzymes.

Growth and division

The rate at which bacteria grow and divide depends in large part on the nutritional status of the environment. The growth and division of a single E. coli cell into identical ‘daughter cells’ may occur in as little as 20–30 min in rich laboratory media, whereas the same process is much slower (1–2 h) in a nutritionally depleted environment. Conversely, even in the best environment, other bacteria such as Mycobacterium tuberculosis may grow much more slowly, dividing every 24 h. When introduced into a new environment, bacterial growth follows a characteristic pattern depicted in Figure 2.6. After an initial period of adjustment (lag phase), cell division rapidly occurs, with the population doubling at a constant rate (generation time), for a period termed log or exponential phase. As nutrients are depleted and toxic products accumulate, cell growth slows to a stop (stationary phase) and eventually enters a phase of decline (death).

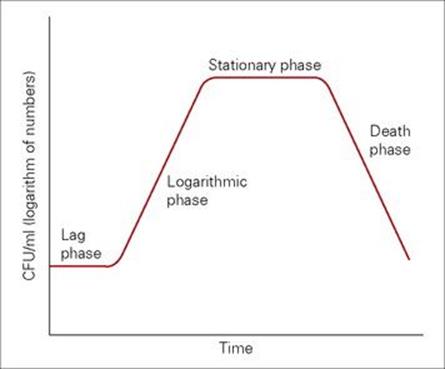
Figure 2.6 The bacterial growth curve. CFU, colony-forming units.

A bacterial cell must duplicate its genomic DNA before it can divide

All bacterial genomes are circular, and their replication begins at a single site known as the origin of replication (termed OriC). A multienzyme replication complex binds to the origin and initiates unwinding and separation of the two DNA strands, using enzymes called helicases and topoisomerases (e.g. DNA gyrase). The separated DNA strands each serve as a template for DNA polymerase. The polymerization reaction involves incorporation of deoxyribonucleotides, which correctly base pair with the template DNA. Two characteristic replication forks are formed, which proceed in opposite directions around the chromosome. The two copies of the total genetic information (genome) produced during replication each comprise one parental strand and one newly synthesized strand of DNA.

Replication of the genome takes approximately 40 min in E. coli, so when these bacteria grow and divide every 20–30 min they need to initiate new rounds of DNA replication before an existing round of replication has finished. In such instances, daughter cells inherit DNA that has already initiated its own replication.

Replication must be accurate

Accurate replication is essential because DNA carries the information that defines the properties and processes of a cell. It is achieved because DNA polymerase is capable of proofreading newly incorporated deoxyribonucleotides and excising those that are incorrect. This reduces the frequency of errors to approximately one mistake (an incorrect base pair) per 10¹⁰ nucleotides copied.

Cell division is preceded by genome segregation and septum formation

The process of cell division (or septation) involves:

• segregation of the replicated genomes

• formation of a septum in the middle of the cell

• division of the cell to give separate daughter cells.

The septum is formed by an invagination of the cytoplasmic membrane and ingrowth of the peptidoglycan cell wall (and outer membrane in Gram-negative bacteria). Septation and DNA replication and genome segregation are not tightly coupled, but are sufficiently well coordinated to ensure that very few daughter cells do not have the correct complement of genomic DNA.

The mechanics of cell division result in reproducible cellular arrangements, when viewed by microscopic examination. For example, cocci dividing in one plane may appear chained (streptococci) or paired (diplococci), while division in multiple planes results in clusters (staphylococci). As with cell shape, these arrangements have served as an important characteristic for bacterial identification.

Bacterial growth and division are important targets for antimicrobial agents

Antimicrobials that target the processes involved in bacterial growth and division include:

• quinolones (ciprofloxacin and levofloxacin), which inhibit the unwinding of DNA by DNA gyrase during DNA replication

• the many inhibitors of peptidoglycan cell wall synthesis (e.g. beta-lactams such as the penicillins, cephalosporins and carbapenems, and glycopeptides such as vancomycin).

These are considered in more detail in Chapter 33.

Gene expression

Gene expression describes the processes involved in decoding the ‘genetic information’ contained within a gene to produce a functional protein or RNA molecule.

Most genes are transcribed into messenger RNA (mRNA)

The overwhelming majority of genes (e.g. up to 98% in E. coli) are transcribed into mRNA, which is then translated into proteins. Certain genes, however, are transcribed to produce ribosomal RNA species (5 S, 16 S, 23 S), which provide a scaffold for assembling ribosomal subunits; others are transcribed into transfer RNA (tRNA) molecules, which together with the ribosome participate in decoding mRNA into functional proteins.

Transcription

The DNA is copied by a DNA-dependent RNA polymerase to yield an RNA transcript. The polymerization reaction involves incorporation of ribonucleotides, which correctly base pair with the template DNA.

Transcription is initiated at promoters

Promoters are nucleotide sequences in DNA that can bind the RNA polymerase. The frequency of transcription initiation can be influenced by many factors, for example:

• the exact DNA sequence of the promoter site

• the overall topology (supercoiling) of the DNA

• the presence or absence of regulatory proteins that bind adjacent to and may overlap the promoter site.

Consequently, different promoters have widely different rates of transcriptional initiation (of up to 3000-fold). Their activities can be altered by regulatory proteins. Sigma factor (a component RNA polymerase) plays an important role in promoter recognition. The presence of several different sigma factors in bacteria enables sets of genes to be switched on simply by altering the level of expression of a particular sigma factor. This is particularly important in controlling the expression of genes involved in spore formation in Gram-positive bacteria.

Transcription usually terminates at specific termination sites

These termination sites are characterized by a series of uracil residues in the mRNA following an inverted repeat sequence, which can adopt a stem-loop structure (which forms as a result of the base-pairing of ribonucleotides) and interfere with RNA polymerase activity. In addition, certain transcripts terminate following interaction of RNA polymerase with the transcription termination protein, rho.

mRNA transcripts often encode more than one protein in bacteria

The bacterial arrangement seen for single genes (promoter- structural-gene-transcriptional-terminator) is described as monocistronic. However, a single promoter and terminator may flank multiple structural genes, a polycistronic arrangement known as an operon. Operon transcription thus results in polycistronic mRNA encoding more than one protein (Fig. 2.7). Operons provide a way of ensuring that protein subunits that make up particular enzyme complexes or are required for a specific biological process are synthesized simultaneously and in the correct stoichiometry. For example, the proteins required for the uptake and metabolism of lactose are encoded by the lac operon. Many of the proteins responsible for the pathogenic properties of medically important microorganisms are likewise encoded by operons, for example:

• cholera toxin from Vibrio cholerae

• fimbriae (pili) of uropathogenic E. coli, which mediate colonization.

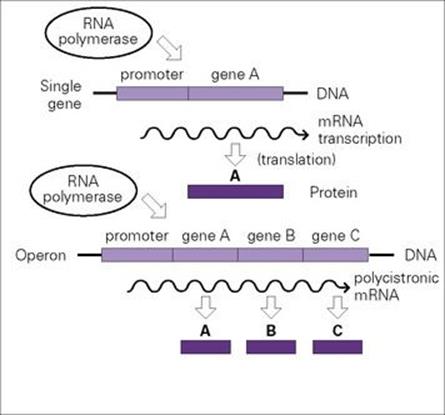
Figure 2.7 Bacterial genes are present on DNA as separate discrete units (single genes) or as operons (multigenes), which are transcribed from promoters to give, respectively, monocistronic or polycistronic messenger RNA (mRNA) molecules; mRNA is then translated into protein.

Translation

The exact sequence of amino acids in a protein (polypeptide) is specified by the sequence of nucleotides found in the mRNA transcripts. Decoding this information to produce a protein is achieved by ribosomes and tRNA molecules in a process known as translation. Each set of three bases (triplet) in the mRNA sequence corresponds to a codon for a specific amino acid. However, there is redundancy in the triplet code resulting in instances of more than one triplet encoding the same amino acid (i.e., also referred to as code degeneracy). Thus, a total of 64 codons encode all 20 amino acids as well as start and stop signal codons.

Translation begins with formation of an initiation complex and terminates at a STOP codon

The initiation complex comprises mRNA, ribosome and an initiator transfer RNA molecule (tRNA) carrying formylmethionine. Ribosomes bind to specific sequences in mRNA (Shine–Dalgarno sequences) and begin translation at an initiation (START) codon, AUG, which hybridizes with a specific complementary sequence (the anti-codon loop) of the initiator tRNA molecule. The polypeptide chain elongates as a result of movement of the ribosome along the mRNA molecule and the recruitment of further tRNA molecules (carrying different amino acids), which recognize the subsequent codon triplets. Ribosomes carry out a condensation reaction, which couples the incoming amino acid (carried on the tRNA) to the growing polypeptide chain.

Translation is terminated when the ribosome encounters one of three termination (STOP) codons: UGA, UAA or UAG.

Transcription and translation are important targets for antimicrobial agents

Such antimicrobial agents include:

• inhibitors of RNA polymerase, such as rifampicin

• a wide array of bacterial protein synthesis inhibitors including macrolides (e.g. erythromycin), aminoglycosides, tetracyclines, chloramphenicol, lincosamides, streptogramins, and oxazolidinones (see Ch. 33).

Regulation of gene expression

Bacteria adapt to their environment by controlling gene expression

Bacteria show a remarkable ability to adapt to changes in their environment. This is predominantly achieved by controlling gene expression, thereby ensuring that proteins are only produced when and if they are required. For example:

• Bacteria may encounter a new source of carbon or nitrogen and as a consequence switch on new metabolic pathways that enable them to transport and use such compounds.

• When compounds such as amino acids are depleted from a bacterium’s environment the bacterium may be able to switch on the production of enzymes that enable it to synthesize the particular molecule it requires de novo.

Expression of many virulence determinants by pathogenic bacteria is highly regulated

This makes sense since it conserves metabolic energy and ensures that virulence determinants are only produced when their particular property is needed. For example, enterobacterial pathogens are often transmitted in contaminated water supplies. The temperature of such water will probably be lower than 25°C and low in nutrients. However, upon entering the human gut there will be a striking change in the bacterium’s environment – the temperature will rise to 37°C, there will be an abundant supply of carbon and nitrogen and a low availability of both oxygen and free iron (an essential nutrient). Bacteria adapt to such changes by switching on or off a range of metabolic and virulence-associated genes.

The analysis of virulence gene expression is one of the fastest growing aspects of the study of microbial pathogenesis. It provides an important insight into how bacteria adapt to the many changes they encounter as they initiate infection and spread into different host tissues.

The most common way of altering gene expression is to change the amount of mRNA transcription

The level of mRNA transcription can be altered by altering the efficiency of binding of RNA polymerase to promoter sites. Environmental changes such as shifts in growth temperature (from 25°C to 37°C) or the availability of oxygen can change the extent of supercoiling in DNA, thereby altering the overall topology of promoters and the efficiency of transcription initiation. However, most instances of transcriptional regulation are mediated by regulatory proteins, which bind specifically to the DNA adjacent to or overlapping the promoter site and alter RNA polymerase binding and transcription. The regions of DNA to which regulatory proteins bind are known as operators or operator sites. Regulatory proteins fall into two distinct classes:

• those that increase the rate of transcription initiation (activators)

• those that inhibit transcription (repressors) (Fig. 2.8).

Genes subject to negative regulation bind repressor proteins. Genes subject to positive regulation need to bind activated regulatory protein(s) to promote transcription initiation.

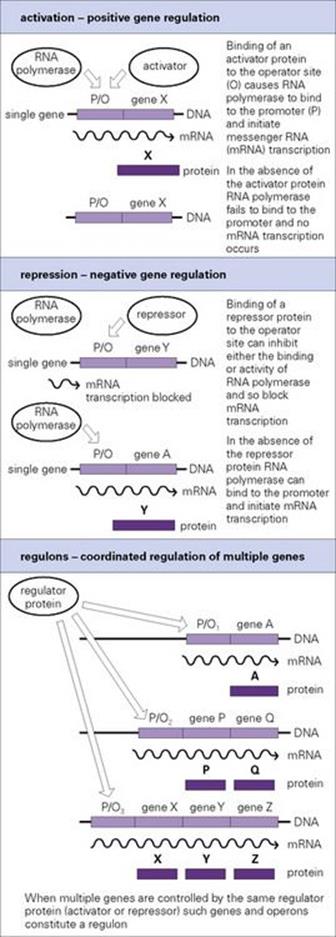
Figure 2.8 Expression of genes in bacteria is highly regulated, enabling them to switch genes on or off in response to changes in available nutrients or other changes in their environment. Genes and operons controlled by the same regulator constitute a regulon.

The principles of gene regulation in bacteria can be illustrated by the regulation of genes involved in sugar metabolism

Bacteria use sugars as a carbon source for growth and prefer to use glucose rather than other less well-metabolized sugars. When growing in an environment containing both glucose and lactose, bacteria such as E. coli preferentially metabolize glucose and at the same time prevent the expression of the lac operon, the products of which transport and metabolize lactose (Fig. 2.9). This is known as catabolite repression. It occurs because the transcriptional initiation of the lac operon is dependent upon a positive regulator, the cAMP-dependent catabolite activator protein (CAP), which is only activated when cAMP is bound. When bacteria grow on glucose the cytoplasmic levels of cAMP are low and so CAP is not activated. CAP is therefore unable to bind to its DNA binding site adjacent to the lac promoter and facilitate transcription initiation by RNA polymerase. When the glucose is depleted, the cAMP concentration rises, resulting in the formation of activated cAMP–CAP complexes, which bind the appropriate site on the DNA, increasing RNA polymerase binding and transcription.

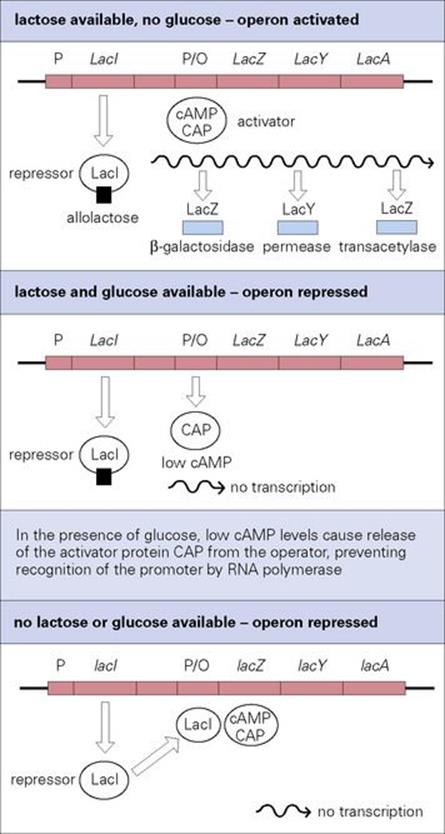
Figure 2.9 Control of the lac operon. Transcription is controlled by the lactose repressor protein (LacI, negative regulation) and by the catabolite activator protein (CAP, positive regulation). In the presence of lactose as the sole carbon source for growth, the lac operon is switched on. Bacteria prefer to use glucose rather than lactose, so if glucose is also present the lac operon is switched off until the glucose has been used.

CAP is an example of a global regulatory protein that controls the expression of multiple genes; it controls the expression of over 100 genes in E. coli. All genes controlled by the same regulator are considered to constitute a regulon (see Fig. 2.8). In addition to the influence of CAP on the lac operon, the operon is also subject to negative regulation by the lactose repressor protein (LacI, see Fig. 2.9). LacI is encoded by the lacI gene, which is located immediately upstream of the lactose operon and transcribed by a separate promoter. In the absence of lactose, LacI binds specifically to the operator region of the lac promoter and blocks transcription. An inducer molecule, allolactose (or its non-metabolizable homologue, isopropyl-thiogalactoside–IPTG) is able to bind to LacI, causing an allosteric change in its structure. This releases it from the DNA, thereby alleviating the repression. The lac operon therefore illustrates the fine tuning of gene regulation in bacteria – the operon is switched on only if lactose is available as a carbon source for cell growth, but remains unexpressed if glucose, the cell’s preferred carbon source, is also present.

Expression of bacterial virulence genes is often controlled by regulatory proteins

An example of such regulation is the production of diphtheria toxin by Corynebacterium diphtheriae (see Ch. 18), which is subject to negative regulation if there is free iron in the growth environment. A repressor protein, DtxR, binds iron and undergoes a conformational change that allows it to bind with high affinity to the operator site of the toxin gene and inhibit transcription. When C. diphtheriae grow in an environment with a very low concentration of iron (i.e. similar to that of human secretions), DtxR is unable to bind iron, and toxin production occurs.

Many bacterial virulence genes are subject to positive regulation by ‘two-component regulators’

These two-component regulators usually comprise two separate proteins (Fig. 2.10):

• one acting as a sensor to detect environmental changes (such as alterations in temperature)

• the other acting as a DNA-binding protein capable of activating (or repressing in some cases) transcription.

In Bordetella pertussis, the causative agent of whooping cough (see Ch. 19), a two-component regulator (encoded by the bvg locus) controls expression of a large number of virulence genes. The sensor protein, BvgS, is a cytoplasmic membrane-located histidine kinase, which senses environmental signals (temperature, Mg^{2 +}, nicotinic acid), leading to an alteration in its autophosphorylating activity. In response to positive regulatory signals such as an elevation in temperature, BvgS undergoes autophosphorylation and then phosphorylates, so activating the DNA-binding protein BvgA. BvgA then binds to the operators of the pertussis toxin operon and other virulence-associated genes and activates their transcription.

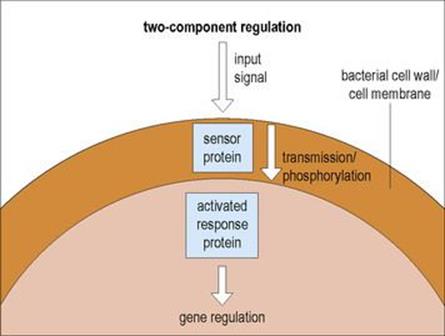
Figure 2.10 Two-component regulation is a signal transduction process that allows cellular functions to react in response to a changing environment. An appropriate environmental stimulus results in autophosphorylation of the sensor protein which, by a phosphotransfer reaction, activates the response protein which affects gene regulation.

In Staphylococcus aureus, a variety of virulence genes are influenced by global regulatory systems, the best studied and most important of which is a two-component regulator termed accessory gene regulator (agr). Agr control is complex in that it serves as a positive regulator for exotoxins secreted late in the bacterial lifecycle (post-exponential phase) but behaves as a negative regulator for virulence factors associated with the cell surface.

Regulation of virulence genes often involves a cascade of activators

For example:

• In B. pertussis, BvgA appears to activate the expression of another regulatory protein, which in turn activates the expression of filamentous haemagglutinin, the major adherence factor produced by B. pertussis.

• The control of virulence gene expression in V. cholerae is under the control of ToxR, a cytoplasmic membrane-located protein, which senses environmental changes. ToxR activates both the transcription of the cholera toxin operon and another regulatory protein, ToxT, which in turn activates the transcription of other virulence genes such as toxin-co-regulated pili, an essential virulence factor required for colonization of the human small intestine.

In some instances the pathogenic activity of bacteria specifically begins when cell numbers reach a certain threshold

Quorum sensing is the mechanism by which specific gene transcription is activated in response to bacterial concentration. While quorum sensing is known to occur in a wide variety of microorganisms, a classic example is the production of biofilms by Pseudomonas aeruginosa in the lungs of cystic fibrosis (CF) patients. The production of these tenacious substances allows P. aeruginosa to establish serious long-term infection in CF patients which is difficult to treat (see Ch. 19; Fig. 19.22). As illustrated in Figure 2.11, when quorum-sensing bacteria reach appropriate numbers, the signalling compounds they produce are at sufficient concentration to activate transcription of specific response genes such as those related to biofilm production. Current research is aimed at better understanding the quorum-sensing process in hopes of finding approaches (e.g. inhibitory compounds) to interfere with this coordinated mechanism of bacterial virulence.

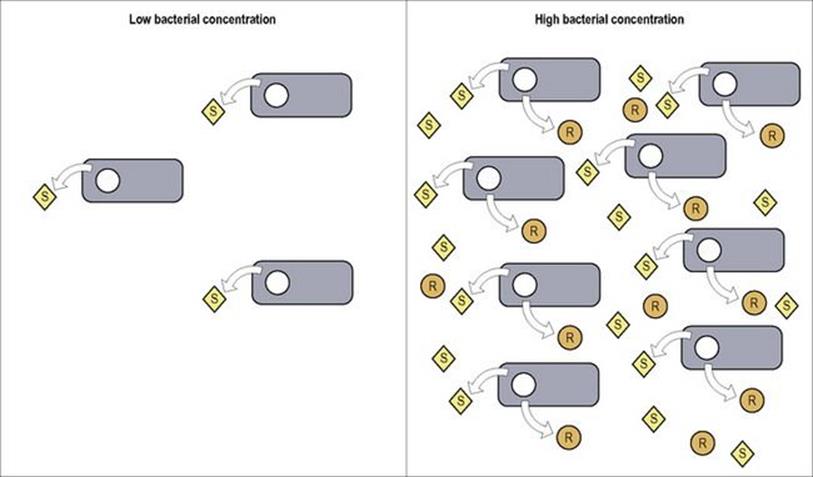
Figure 2.11 Quorum sensing bacteria produce signalling compounds (S) which, in sufficient concentration, bind to receptors which activate transcription of specific response genes (R) (e.g. for biofilm production, etc.).

Survival under adverse conditions

Some bacteria form endospores

Certain bacteria can form highly resistant spores – endospores – within their cells, and these enable them to survive adverse conditions. They are formed when the cells are unable to grow (e.g. when environmental conditions change or when nutrients are exhausted), but never by actively growing cells. The spore has a complex multilayered coat surrounding a new bacterial cell. There are many differences in composition between endospores and normal cells, notably the presence of dipicolinic acid and a high calcium content, both of which are thought to confer the endospore’s extreme resistance to heat and chemicals.

Because of their resistance, spores can remain viable in a dormant state for many years, re-converting rapidly to normal existence when conditions improve. When this occurs, a new bacterial cell grows out from the spore and resumes vegetative life. Endospores are abundant in soils, and those of the Clostridium and Bacillus are a particular hazard (Fig. 2.12). Tetanus and anthrax caused by these bacteria are both associated with endospore infection of wounds, the bacteria developing from the spores once in appropriate conditions.

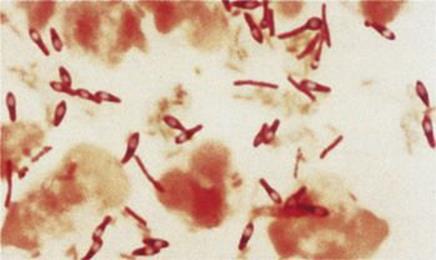
Figure 2.12 Clostridium tetani with terminal spores.

Mobile genetic elements

The bacterial chromosome represents the primary reservoir of genetic information within the cell. However, a variety of additional genetic elements may also be present which are capable of independently moving to different locations within a cell or between cells (also termed horizontal gene transfer).

Many bacteria possess small, independently replicating (extrachromosomal) nucleic acid molecules termed plasmids and bacteriophages

Plasmids are independent, self-replicating, circular units of dsDNA, some of which are relatively large (60–120 kb) while others are quite small (1.5–15 kb). Plasmid replication is similar to the replication of genomic DNA, though there may be some differences. Not all plasmids are replicated bidirectionally – some have a single replication fork, others are replicated like a ‘rolling circle’. The number of plasmids per bacterial cell (copy number) varies for different plasmids, ranging from 1 to 1000 copies/cell. The rate of initiation of plasmid replication determines the plasmid copy number; however, larger plasmids generally tend to have lower copy numbers than smaller plasmids. Some plasmids (broad host-range plasmids) are able to replicate in many different bacterial species, others have a more restricted host range.

Plasmids contain genes for replication, and in some cases for mediating their own transfer between bacteria (tra genes). Plasmids may additionally carry a wide variety of genes (up to 100 on larger plasmids) which can confer phenotypic advantages to the host bacterial cell.

Widespread use of antimicrobials has applied a strong selection pressure in favour of bacteria able to resist them

In the majority of cases, resistance to antimicrobials is due to the presence of resistance genes on conjugative plasmids (R plasmids; see Ch. 33). These are known to have existed before the era of mass antibiotic treatments, but they have become widespread in many species as a result of selection. R plasmids may carry genes for resistance to several antimicrobials. For example, the common R plasmid, R1, confers resistance to ampicillin, chloramphenicol, kanamycin, streptomycin and sulphonamides, and there are many others conferring resistance to a wide spectrum of antimicrobials. R plasmids can recombine so that individual plasmids can be responsible for new combinations of multiple drug resistance.

Plasmids can carry virulence genes

Plasmids may encode toxins and other proteins that increase the virulence of microorganisms. For example:

• The virulent enterotoxinogenic strains of E. coli that cause diarrhea produce one of two different types of plasmid-encoded enterotoxin. The enterotoxin alters the secretion of fluid and electrolytes by the intestinal epithelium (see Ch. 22).

• In Staphylococcus aureus, both an enterotoxin and a number of enzymes involved in bacterial virulence (haemolysin, fibrinolysin) are encoded by plasmid genes.

The production of toxins by bacteria, and their pathologic effects, is discussed in detail in Chapter 17.

Plasmids are valuable tools for cloning and manipulating genes

Molecular biologists have generated a wealth of recombinant plasmids to use as vectors for genetic engineering (Fig. 2.13). Plasmids can be used to transfer genes across species barriers so that defined gene products can be studied or synthesized in large quantities in different recipient organisms.

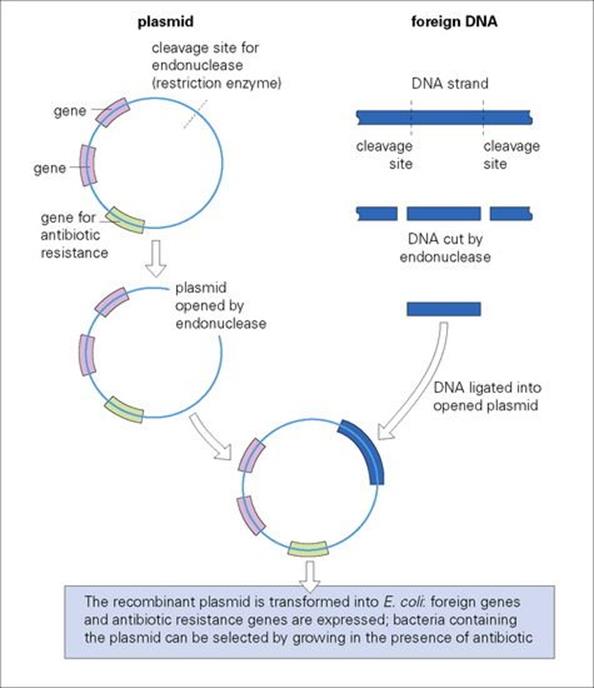
Figure 2.13 The use of plasmid vectors to introduce foreign DNA in E. coli – a basic step in gene cloning.

Bacteriophages are bacterial viruses that can survive outside as well as inside the bacterial cell

Bacteriophages differ from plasmids in that their reproduction usually leads to destruction of the bacterial cell. In general, bacteriophages consist of a protein coat or head (capsid), which surrounds nucleic acid which may be either DNA or RNA but not both. Some bacteriophages may also possess a tail-like structure which aids them in attaching to and infecting their bacterial host. As illustrated in Figure 2.14 for DNA-containing bacteriophages, the virus attaches and injects its DNA into the bacterium, leaving the protective protein coat behind. Virulent bacteriophages instigate a form of molecular mutiny to commandeer cellular nucleic acid and protein to produce new virus DNA and protein. Many new virus particles (virions) are then assembled and released into the environment as the bacterial cell ruptures (lyses), thus allowing the cycle to begin again.

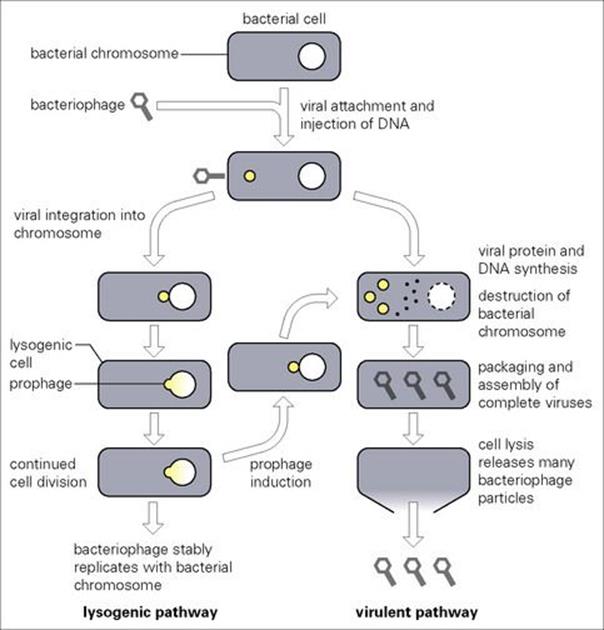
Figure 2.14 The life cycle of bacteriophages.

While destruction of the host is always the direct consequence of virulent bacteriophage infection, temperate bacteriophages may exercise a ‘choice’. Following infection, they may immediately reproduce in a manner similar to their virulent counterparts. However, in some instances they may insert into the bacterial chromosome. This process, termed lysogeny, does not kill the cell since the integrated viral DNA (now called a prophage) is quiescently carried and replicated within the bacterial chromosome. New characteristics may be expressed by the cell as a result of prophage presence (prophage conversion) which, in some instances, may increase bacterial virulence (e.g. the gene for diphtheria toxin resides on a prophage). Nevertheless, this latent state is eventually destined to end, often in response to some environmental stimulus inactivating the bacteriophage repressor which normally maintains the lysogenic condition. During this induction process, the viral DNA is excised from the chromosome and proceeds to active replication and assembly, resulting in cell lysis and viral release.

Whether virulent or temperate, bacteriophage infection ultimately results in death of the host cell which, given current problems with multiple resistance, has sparked a renewed interest in their use as ‘natural’ antimicrobial agents. However, a variety of issues related to dosing, delivery, quality control, etc. have impeded the use of ‘bacteriophage therapy’ in routine clinical practice.

Transposition

Transposable elements are DNA sequences that can jump (transpose) from a site in one DNA molecule to another in a cell. This movement does not rely on host-cell (homologous) recombination pathways which require extensive similarity between the resident and incoming DNA. Instead, movement involves short target sequences in the recipient DNA molecule where recombination/insertion is directed by the mobile element (site-specific recombination).

While plasmid transfer involves the movement of genetic information between bacterial cells, transposition is the movement of such information between DNA molecules. The most extensively studied transposable elements are those found in E. coli and other Gram-negative bacteria, although examples are also found in Gram-positive bacteria, yeast, plants and other organisms.

Insertion sequences are the smallest and simplest ‘jumping genes’

Insertion sequence elements (ISs) are < 2 kb in length and only encode functions such as the transposase enzyme, which is required for transposition from one DNA site to another. At the ends of ISs, there are usually short inverted repeat sequences (23 nucleotides long in IS1), which are also important in the process of locating and inserting into a DNA target (Fig. 2.15A). During the transposition process, a portion of the target sequence is duplicated, resulting in short direct repeat sequences (the same sequence in the same orientation) on each side of the newly inserted IS element. Many aspects of the target selection process remain unclear. While A/T-rich regions of DNA appear to be preferred, some ISs are highly selective, whereas others are generally indiscriminate. Transposition does not rely on enzymatic processes typically used by the cell for homologous recombination (recombination between highly related DNA molecules) and is thus termed ‘illegitimate recombination’. The result is a typically small number of ISs in bacterial genomes. In E. coli, IS1 is found in 6–10 copies; and five copies in IS2 and 3. Multiple IS copies serve an important function as ‘portable regions of homology’ throughout a bacterial genome where homologous recombination may occur between different DNA regions or molecules (e.g. chromosome and plasmid) carrying the same IS sequence. Two IS elements inserting relatively near to each other would allow the entire region to become transposable, further promoting the potential for genetic movement and exchange in bacterial populations.

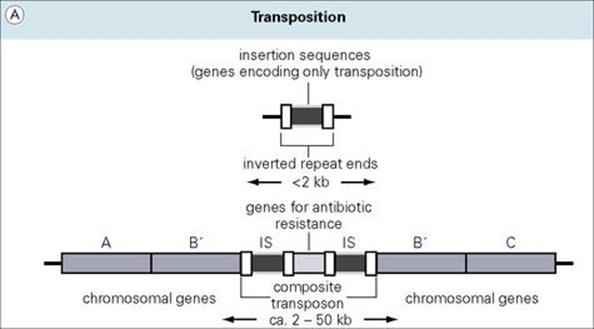
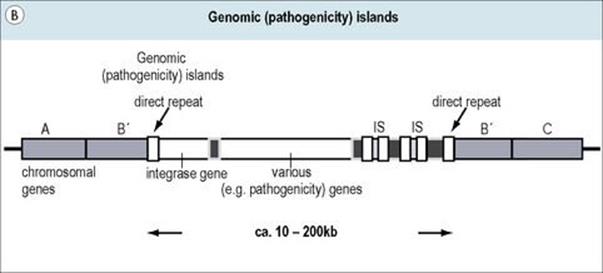
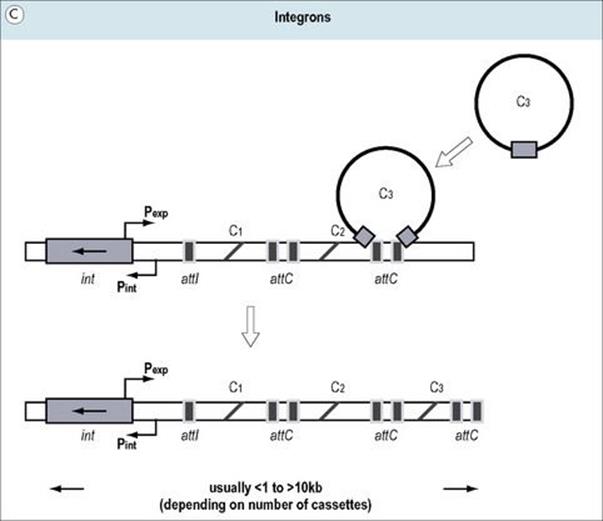
Figure 2.15 (A) Transposons (jumping genes) can move from one DNA site to another; they inactivate the recipient gene into which they insert. Transposons often contain genes which confer resistance to antibiotics. (B) Genomic islands are regions of DNA with ‘signature sequences’ (e.g. direct repeats) indicative of mobility. Their encoded functions increase bacterial fitness (e.g. pathogenicity). (C) Integrons are genetic regions into which independent open reading frames, also termed gene cassettes, can integrate and become functional (e.g. under control of the promoter P_exp). The integration process occurs by site-specific recombination between circular cassettes and their recipient integron, which is directed by an integrase gene (intl) with promoter P_int and an associated attachment site (attl).

Transposons are larger, more complex elements, which encode multiple genes

Transposons are > 2 kb in size and contain genes in addition to those required for transposition (often encoding resistance to one or more antibiotics) (Fig. 2.15A). Furthermore, virulence genes, such as those encoding heat-stable enterotoxin from E. coli, have been found on transposons.

Transposons can be divided into two classes:

1. composite transposons, where two copies of an identical IS element flank antibiotic-resistance genes (kanamycin resistance in Tn5)

2. simple transposons, such as Tn3 (encoding resistance to beta-lactams).

ISs at the ends of composite transposons may be in either the same or inverted orientation (i.e. direct or indirect repeats). Although part of the composite transposon structure, the terminal IS elements are fully intact and capable of independent transposition.

Simple transposons move only as a single unit, containing genes for transposition and other functions (e.g. antibiotic resistance) with short, inversely oriented sequences (indirect repeats) at each end.

Mobile genetic elements promote a variety of DNA rearrangements which may have important clinical consequences

The ease with which transposons move into or out of DNA sequences means that transposition can occur:

• from host genomic DNA harbouring a transposon to a plasmid

• from one plasmid to another plasmid

• from a plasmid to genomic DNA.

Transposition onto a broad host-range conjugative plasmid can lead to the rapid dissemination of resistance among different bacteria. The transposition process (whether by ISs or transposons) can be deleterious if insertion occurs within, and disrupts, a functional gene. However, transpositional mutagenesis has been effectively utilized in the molecular biology laboratory to produce extremely specific mutations without the harmful secondary effects often seen with more generally acting chemical mutagens.

Other mobile elements also behave as portable cassettes of genetic information

Pathogenicity islands (Fig. 2.15B) are a special class of mobile genetic elements containing groups of coordinately controlled virulence genes, often with ISs, direct repeat sequences, etc. at their ends. Though originally observed in uropathogenic E. coli (encoding haemolysins and pili), pathogenicity islands have now been found in a number of additional bacterial species including Helicobacter pylori, Vibrio cholerae, Salmonella spp., Staphylococcus aureus, and Yersinia spp. Such regions are not found in non-pathogenic bacteria, may be quite large (up to hundreds of kilobases), and tend to be unstable (spontaneously lost). Differences in DNA sequence (G+C content) between such elements and their host genomes and the presence of transposon-like genes support speculation regarding their origin and movement from unrelated bacterial species. The term ‘genomic island’ has been given to DNA sequences similar to pathogenicity islands but lacking functional genes for movement.

Integrons are mobile genetic elements that are able to use site-specific recombination to acquire new genes in ‘cassette-like’ fashion and express them in a coordinated manner (Fig. 2.15C). Integrons lack terminal repeat sequences and certain genes characteristic of transposons but, similar to transposable elements, often carry genes associated with antibiotic resistance (see Fig. 33.5).

Another important type of mobile element includes staphylococcal cassette chromosomes (SCCs) such as SCCmec, which not only encodes methicillin resistance but also serves as a recombinational hot spot for the acquisition of other mobile sequences. SCCs influencing virulence and antimicrobial resistance include SCCcapI encoding capsular polysaccharide I and SCC₄₇₆ and SCCmercury conferring resistance to fusidic acid and mercury, respectively. The arginine catabolic mobile element (ACME) is a cassette-like element potentially contributing to the virulence of the important USA300 community-associated methicillin-resistant Staphylococcus aureus (MRSA) strain originally reported in the United States but now globally disseminated. An example of the interrelationship between the bacterial core genome and additional mobile genetic elements is depicted in Figure 2.16.

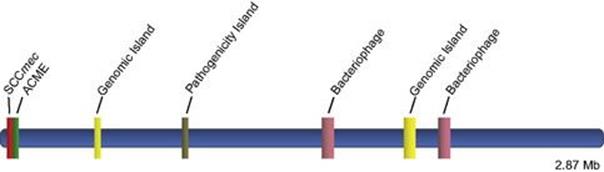
Figure 2.16 Linear depiction of the interrelationship between the USA300 MRSA core genome and key mobile genetic elements SCCmec, ACME, two different bacteriophages, two different genomic islands, and a pathogenicity island encoding antibiotic resistance and a variety of virulence factors.

Mutation and gene transfer

Bacteria are haploid organisms, their chromosomes containing one copy of each gene. Replication of the DNA is a precise process resulting in each daughter cell acquiring an exact copy of the parental genome. Changes in the genome can occur by two processes:

• mutation

• recombination.

These processes result in progeny with phenotypic characteristics that may differ from those of the parent. This is of considerable significance in terms of virulence and drug resistance.

Mutation

Changes in the nucleotide sequence of DNA can occur spontaneously or under the influence of external agents

While mutations may spontaneously occur as a result of errors in the DNA replication process, a variety of chemicals (mutagens) bring about direct changes in the DNA molecule. A classic example of such an interaction involves compounds known as nucleotide-base analogues. These agents mimic normal nucleotides during DNA synthesis but are capable of multiple pairing with a counterpart on the opposite strand. While 5-bromouracil is considered a thymine analogue, for example, it may also behave as a cytosine, thus allowing the potential for a change from T-A to C-G in a replicating DNA duplex. Other agents may cause changes by inserting (intercalating) and distorting the DNA helix or by interacting directly with nucleotide bases to chemically alter them.

Regardless of their cause, changes in DNA may generally be characterized as follows.

• Point mutations: changes in single nucleotides, which alter the triplet code. Such mutations may result in:

• no change in the amino acid sequence of the protein encoded by the gene, because the different codons specify the same amino acid and are therefore silent mutations

• an amino acid substitution in the translated protein (missense mutation), which may or may not alter its stability or functional properties

• the formation of a STOP codon, causing premature termination and production of a truncated protein (nonsense mutation).

• More comprehensive changes in the DNA, which involve deletion, replacement, insertion or inversion of several or many bases. The majority of these changes are likely to harm the organism, but a few may be beneficial and confer a selective advantage through the production of different proteins.

Bacterial cells are not defenceless against genetic damage

Since the bacterial genome is the most fundamental molecule of identity in the cell, enzymatic machinery is in place to protect it against both spontaneously occurring and induced mutational damage. As illustrated in Figure 2.17, these DNA repair processes include the following:

• Direct repair which either reverses or simply removes the damage. This may be regarded as ‘first line’ defence. For example, abnormally linked pyrimidine bases in DNA (pyrimidine dimers) resulting from ultraviolet radiation are directly reversed by a light-dependent enzyme through a repair process known as photoreactivation.

• Excision repair where damage in a DNA strand is recognized by an enzymatic ‘housekeeping’ process and excised, followed by repair polymerization to fill the gap using the intact complementary DNA strand as a template. This is also a primary form of defence, since the goal is to correct damage before it encounters and potentially interferes with the moving DNA replication fork. Some of these housekeeping genes are also part of an inducible system (SOS repair), which is activated by the presence of DNA damage to quickly respond and effect repair.

• ‘Second line’ repair which operates when DNA damage has reached a point where it is more difficult to correct. When normal DNA replication processes are blocked, permissive systems may allow the interfering damage to be inaccurately corrected, allowing errors to occur but improving the probability of cell survival. In other instances, where damage has passed the replication fork, post-replication or recombinational repair processes may ‘cut and paste’ to construct error-free DNA from multiple copies of the sequence found in parental and daughter strands.

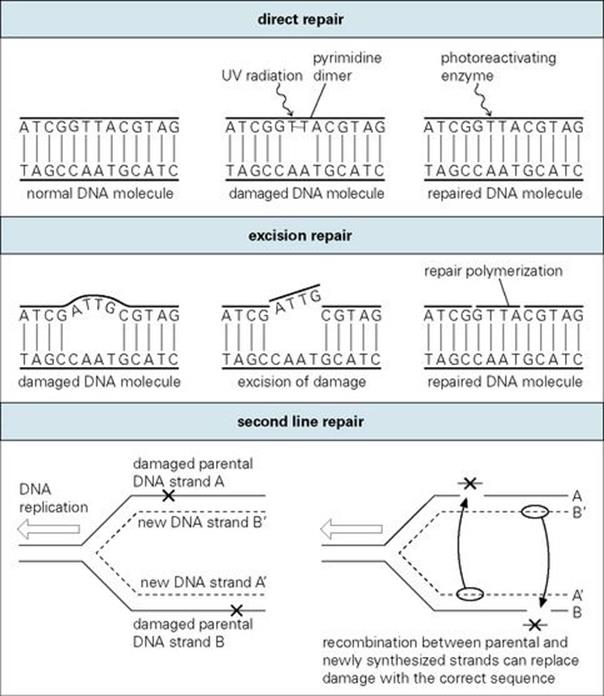
Figure 2.17 Mechanisms of DNA repair.

Bacterial DNA repair has provided a model for understanding similar, more complex processes in humans

DNA repair mechanisms appear to be present in all living organisms as a defence against environmental damage. The study of these processes in bacteria has led to an important understanding of general principles that apply to higher organisms, including issues of cancer and aging in humans. For example, several human disorders are known to be DNA-repair related, including:

• xeroderma pigmentosum, characterized by extreme sensitivity to the sun, with great risk for development of a variety of skin cancers such as basal cell carcinoma, squamous cell carcinoma and melanoma

• Cockayne syndrome, characterized by progressive neurologic degeneration, growth retardation, and sun sensitivity not associated with cancer

• trichothiodystrophy, characterized by mental and growth retardation, fragile hair deficient in sulphur, and sun sensitivity not associated with cancer.

Gene transfer and recombination

New genotypes arise when genetic material is transferred from one bacterium to another. In such instances, the transferred DNA either:

• recombines with the genome of the recipient cell

• or is on a plasmid capable of replication in the recipient without recombination.

Recombination can bring about large changes in the genetic material, and since these events usually involve functional genes, they are likely to be expressed phenotypically. DNA can be transferred from a donor cell to a recipient cell by:

• transformation

• transduction

• conjugation.

Transformation

Some bacteria can be transformed by DNA present in their environment

Certain bacteria such as Streptococcus pneumoniae, Bacillus subtilis, Haemophilus influenzae and Neisseria gonorrhoeae are naturally ‘competent’ to take up DNA fragments from related species across their cell walls. Such DNA fragments may be present in the environment of the competent cell as a result of lysis of other organisms, the release of their DNA and its cleavage into smaller fragments. Once taken into the cell, chromosomal DNA must recombine with a homologous segment of the recipient’s chromosome to be stably maintained and inherited. If the DNA is completely unrelated, the absence of homology prevents recombination and the DNA is degraded. However, plasmid DNA may be transformed into a cell and expressed without recombination. Thus, transformation has served as a powerful tool for molecular genetic analysis of bacteria (Fig. 2.18).

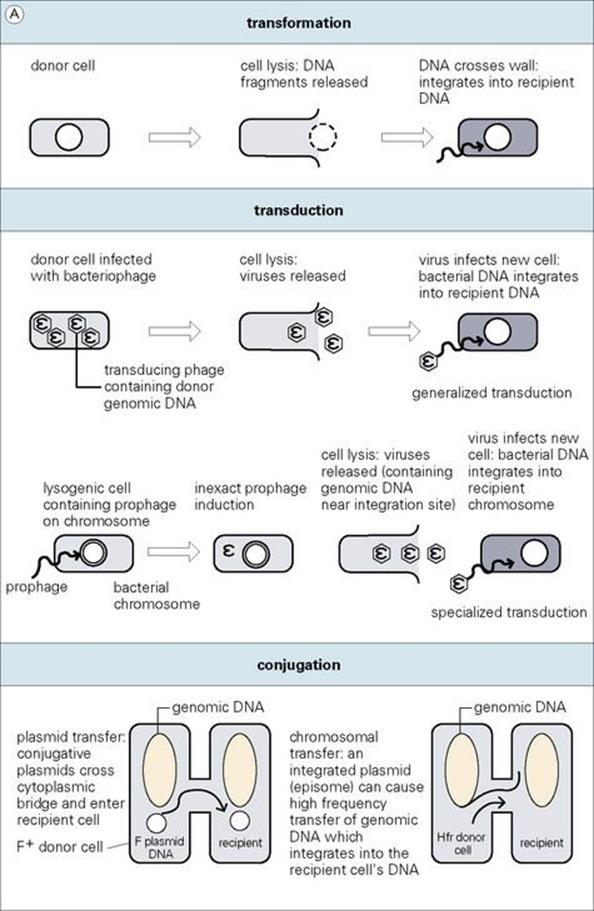
Figure 2.18 Different ways in which genes can be transferred between bacteria. With the exception of plasmid transfer, donor DNA integrates into the recipient’s genome by a process of either homologous or illegitimate (in the case of transposons) recombination.

Most bacteria are not naturally competent to be transformed by DNA, but competence can be induced artificially by treating cells with certain bivalent cations and then subjecting them to a heat shock at 42°C or by electric shock treatment (electroporation).

Prior to uptake by competent cells, DNA is extracellular, unprotected, and thus vulnerable to destruction by environmental extremes (e.g. DNA-degrading enzymes – DNases). Thus, it is the least important mechanism of gene transfer from the standpoint of clinical relevance (e.g. probability of transfer within a patient).

Transduction

Transduction involves the transfer of genetic material by infection with a bacteriophage

During the process of virulent bacteriophage replication (or temperate bacteriophages exercising the direct lysis option), other DNA in the cell (genomic or plasmid) is occasionally erroneously packaged into the virus head, resulting in a ‘transducing particle’, which can attach to and transfer the DNA into a recipient cell. If chromosomal, the DNA must be incorporated into the recipient genome by homologous recombination to be stably inherited and expressed. As with transformation, plasmid DNA may be transduced and expressed in a recipient without recombination. In either case, this type of gene transfer is known as generalized transduction (see Fig. 2.18).

Another form of transduction occurs with ‘temperate’ bacteriophages, since they integrate at specialized attachment sites in the bacterial genome. As these prophages prepare to enter the lytic cycle, they occasionally incorrectly excise from the site of attachment. This can result in phages containing a piece of bacterial genomic DNA adjacent to the attachment site. Infection of a recipient cell then results in a high frequency of recombinants where donor DNA has recombined with the recipient genome in the vicinity of the attachment site. Since this ‘specialized transduction’ is based on specific chromosome–prophage interaction, only genomic DNA, and not plasmids, is transferred by this process.

In contrast to transformation, transduced DNA is always protected, thus increasing its probability of successful transfer and potential clinical relevance. However, bacteriophages are extremely host-specific ‘parasites’ and therefore unable to move any DNA between bacteria of different species.

Conjugation

Conjugation is a type of bacterial ‘mating’ in which DNA is transferred from one bacterium to another

Conjugation is dependent upon the tra genes found in ‘conjugative’ plasmids which, among other things, encode instructions for the bacterial cell to produce a sex pilus – a tube-like appendage which allows cell-to-cell contact to insure the protected transfer of a plasmid DNA copy from a donor cell to a recipient (see Fig. 2.18). Since the tra genes take up genetic space, ‘conjugative’ plasmids are generally larger than non-conjugative ones.

Occasionally, conjugative plasmids such as the fertility plasmid (F plasmid or F factor) of E. coli integrate into the bacterial genome (e.g., facilitated by identical IS elements on both molecules as noted earlier), and such integrated plasmids are called episomes. When an integrated F episome attempts conjugative transfer, the duplication-transfer process eventually moves into regions of adjacent genomic DNA, which are carried along from the donor cell into the recipient. Such strains, in contrast to cells containing the unintegrated F plasmid, mediate high-frequency transfer and recombination of genomic DNA (Hfr strains). However, conjugation with Hfr donor cells does not result in complete transfer of the integrated plasmid. Thus, the recipient cell does not become Hfr and is incapable of serving as a conjugation donor. The circular nature of the bacterial genome and the relative ‘map’ positions of different genes were established using interrupted mating of Hfr strains.

When a non-conjugative plasmid is present in the same cell as a conjugative plasmid, they are sometimes transferred together into the recipient cell by a process known as mobilization. Conjugative transfer of plasmids with resistance genes has been an important cause of the spread of resistance to commonly used antibiotics within and between many bacterial species, since no recombination is required for expression in the recipient. Of all the mechanisms for gene transfer, this rapid and highly efficient movement of genetic information through bacterial populations is clearly of the highest clinical relevance.

The genomics of medically important bacteria

Advances in DNA sequencing techniques are leading to an ever-increasing number of bacterial pathogens for which the total genomic sequence is known (Box 2.1). This evolving database represents a powerful resource with enormous potential application for the understanding and treatment of infectious disease. At present, the utilization of this information is in its infancy; nevertheless, several instances where sequence-based information will be extremely useful in the study of clinically important microorganisms have already emerged, as described below.

Box 2.1 Representative Bacterial Pathogens whose Genomic Sequence is Largely Known

Acinetobacter baumannii, Bacillus anthracis, Bacteroides fragilis, Bartonella henselae, Bartonella quintana, Bordetella bronchiseptica, Bordetella parapertussis, Bordetella pertussis, Borrelia burgdorferi, Borrelia garinii, Brucella abortus, Brucella melitensis, Burkholderia cepacia, Burkholderia mallei, Burkholderia pseudomallei, Campylobacter jejuni, Chlamydia trachomatis, Chlamydophila pneumoniae, Chlamydophila psittaci, Clostridium botulinum, Clostridium difficile, Clostridium perfringens, Clostridium tetani, Corynebacterium diphtheriae, Coxiella burnetii, Enterobacter cloacae, Enterococcus faecalis, Enterococcus faecium, Escherichia coli, Francisella tularensis, Haemophilus ducreyi, Haemophilus influenzae, Helicobacter pylori, Klebsiella pneumoniae, Legionella pneumophila, Leptospira interrogans, Listeria monocytogenes, Moraxella catarrhalis, Mycobacterium avium, Mycobacterium bovis, Mycobacterium leprae, Mycobacterium smegmatis, Mycobacterium tuberculosis, Mycoplasma genitalium, Mycoplasma pneumoniae, Neisseria gonorrhoeae, Neisseria meningitidis, Pasteurella multocida, Propionibacterium acnes, Proteus mirabilis, Pseudomonas aeruginosa, Rickettsia prowazekii, Rickettsia typhi Wilmington, Salmonella Dublin, Salmonella enterica Choleraesuis, Salmonella enteritidis, Salmonella paratyphi, Salmonella typhi, Salmonella typhimurium, Shigella boydii, Shigella dysenteriae, Shigella flexneri, Shigella sonnei, Staphylococcus aureus, Staphylococcus epidermidis, Streptococcus agalactiae, Streptococcus mutans, Streptococcus pneumoniae, Streptococcus pyogenes, Treponema pallidum, Ureaplasma urealyticum, Vibrio cholerae, Vibrio parahaemolyticus, Vibrio vulnificus, Yersinia enterocolitica, Yersinia pestis, Yersinia pseudotuberculosis

Application of genomics facilitates identification

• Identification and classification. The genes encoding ribosomal RNA (16 S, 23 S and 5 S) are typically found together in an operon where their transcription is coordinated (Fig. 2.19). This rDNA operon is found at least once and often in multiple copies distributed around the chromosome, depending on the bacterial species (Borrelia burgdorferi has one copy; Staphylococcus aureus has 5–6). While the rDNA operon contains many conserved sequences (identical in different bacterial species), a portion of the 16 S- and 23 S-encoding regions have been found to be species specific. In between them, an ‘internally transcribed spacer’ (ITS) region exhibits variability that may have utility in differentiating closely related bacterial isolates. Such information clearly has potential for future application in approaches to the rapid identification, classification and epidemiology of clinically important microorganisms (see Chs 31 and 36).

• Resistance to antimicrobial agents. Genes specifically mediating antimicrobial resistance are well known (see Ch. 33). However, total genome sequencing provides more detailed information to insure their detection and allows a global overview where multiple loci may interact to effect resistance. For example, methicillin resistance in Staphylococcus aureus is influenced by a number of genes (e.g. mecA, femA, femB, murE, etc.) at different chromosomal locations.

• Molecular epidemiology. While a variety of phenotypic and genotypic methods have been employed to assess interrelationships in clinical isolates (see Ch. 36), epidemiologic analysis is now moving toward a more sequence-based approach. In contrast to earlier methods, sequence data are highly portable (internet transfer, etc.), less ambiguous (encoded entirely in the characters A, T, G and C, corresponding to the four bases adenine, thymine, guanine and cytosine, respectively), and easily stored in databases. In one approach, sequences from the internal regions of six or seven ‘housekeeping’ (essential) genes are compared to assess the epidemiologic relatedness of different isolates (multi-locus sequence typing, MLST). However, which chromosomal regions will ultimately provide the most epidemiologically relevant information in different bacterial pathogens will become clearer as additional genomes are sequenced.

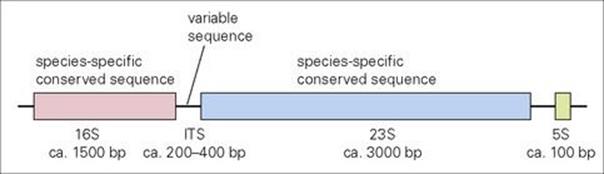
Figure 2.19 Typical arrangement of the bacterial operon encoding ribosomal RNA. Sizes of the genes for 16 S, 23 S, 5 S rRNA and the internally transcribed spacer (ITS) region are indicated in nucleotide base pairs (bp). Regions encoding sequences helpful for species identification or epidemiology are indicated.

Various approaches to the detection and utilization of genomic sequence information exist

Methods such as the polymerase chain reaction (PCR) and nucleic acid probes have clearly had a pivotal role in providing sequence-based answers to clinical microbiology questions (see Ch. 36). Nevertheless, the massive amounts of genomic sequence currently being generated have spawned innovative approaches aimed at extracting the maximum amount of information from the large databases which have been created.

DNA microarrays provide a means for the ‘parallel processing’ of genomic information

Traditionally, molecular biology has operated by analysing one gene in one experiment. While yielding important information, this approach is time consuming and does not afford ready access to the information (chromosomal organization and multiple-gene interaction) contained within genomic-sequence databases. Microarrays represent a new approach to this issue where information may be obtained from multiple queries simultaneously posed to a genomic-sequence database (parallel processing). DNA microarrays are based on the principles of nucleic hybridization (A pairs with T; G pairs with C). While there are a number of variations on the theme, the general format is the arrangement of samples (e.g. gene sequences) in a known matrix on a solid support (nylon, glass, etc.). Using specialized robotics, individual ‘spots’ may be less than 200 mm in diameter, allowing a single array (often called a DNA chip) to contain thousands of spots. Different fluorescently labelled probes of known sequence may then be simultaneously applied followed by monitoring to detect whether complementary binding has occurred.

At present, DNA microarrays are finding use in two main applications: identification of mutations and studies on gene expression

In a number of instances, specific point mutations are clinically important in pathogenic bacteria. Since these changes involve only one nucleotide base they are often referred to as single nucleotide polymorphisms (SNPs). Resistance to the quinolone class of antibiotics, for example, may result from a single base change within the bacterial gyrA gene (see Ch. 33). In the past, such mutations have been detected by PCR amplification of the desired gyrA region followed by DNA sequencing and analysis. As illustrated in Figure 2.20A, DNA microarrays allow gyrA amplicons from different bacterial isolates to be applied to the same chip. Two gyrA probes (wild type, fluorescently labelled red; mutant, fluorescently labelled green) are applied to the array under conditions so stringent that only 100% homology will result in hybridization. In this way, the presence or absence of the specific mutation may be quickly and accurately assessed in a large number of isolates simultaneously.

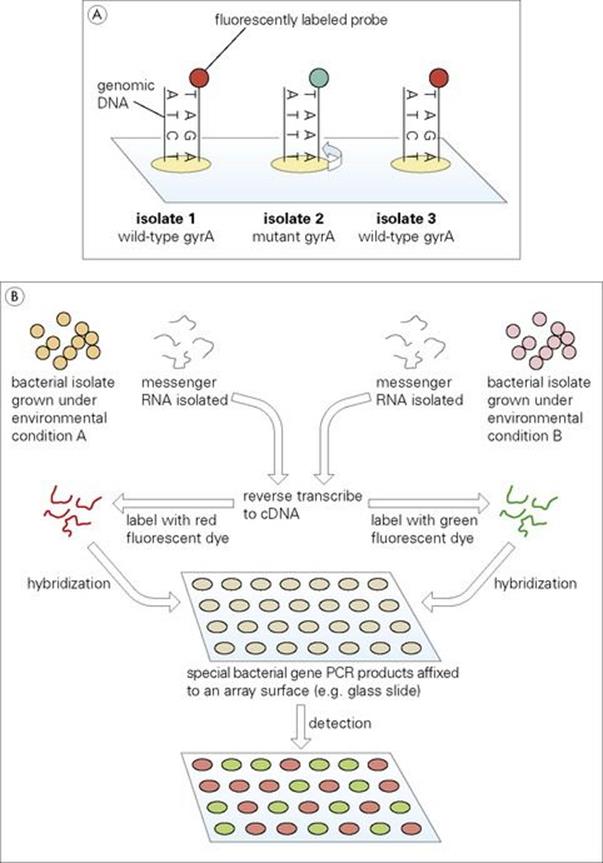
Figure 2.20 (A) Microarray detection of mutations and (B) analysis of gene expression.

Studies of gene expression are extremely important to the understanding of numerous bacterial processes, including virulence. For example, analysis might involve a comparison of gene expression (transcription) in an organism under different environmental conditions (Fig. 2.20B). In such an experiment, genomics can provide data allowing sequences from every known chromosomal gene of the organism to be applied to a unique position on the chip. Messenger RNA (the result of gene expression) may be isolated from the same bacteria grown under either environmental condition A or B. Using the enzyme reverse transcriptase in a process similar to that naturally employed by retroviruses (see Ch. 3), the mRNA is copied into complementary DNA (termed cDNA). Different fluorescent dyes (red or green) are bound to the A or B cDNA, respectively, which is then allowed to hybridize to complementary sequences on the chip. Array spots with red fluorescence will indicate genes expressed in environment A. Those appearing green will correspond to genes active in environment B, while yellow spots (red + green) will indicate genes active under both conditions.

Through innovative technologies such as DNA microarrays, and other approaches which may as yet only exist in an inquisitive mind, genomics will clearly play a major role in our understanding and treatment of infectious disease in the years ahead.

Major groups of bacteria

Detailed summaries of members of the major bacterial groups are given in the Pathogen Parade appendix.

Key Facts

• Bacteria are prokaryotes. Their DNA is not contained within a nucleus and there are relatively few cytoplasmic organelles.

• The cell wall is a key structure in metabolism, virulence and immunity. Its staining characteristics define the two major divisions: the Gram-positive and Gram-negative bacteria. Flagella may be present and confer motility.

• Bacteria metabolize aerobically and anaerobically and can utilize a range of substrates.

• The bacterial cell walls and their reproductive processes are targets for antimicrobial agents.

• Transcription of bacterial DNA may involve single or multiple genes. The arrangement of promoter and terminal sequences flanking multiple genes forms an operon.

• Bacteria can regulate gene expression to optimize exploitation of their environment.

• Plasmids and bacteriophages are independently replicating extrachromosomal agents. Plasmids may carry genes that affect resistance to antimicrobials or virulence.

• Genetic material can be carried from one bacterium to another in several ways; this can result in the rapid spread of resistance to antimicrobials.

• Genomics is revolutionizing the study and the control of bacterial infections.

Conflicts

Bacteria have many ways of coming out top in the conflict with the host. A number produce highly resistant spores that can survive for long periods in the external world, increasing the chances of infection. Once in the host there are many ways of evading host responses. For example, some hide within cells, some have external surfaces that prevent host cells binding to them, others suppress host immunity. Perhaps the most significant advantage bacteria have in their conflict with the host is their ability to sidestep the antibiotics designed to inhibit or eliminate them. Either by mutation, facilitated by their rapid generation/duplication time, or by externally acquired genetic information they are able to engage in a game of ‘cat and mouse’, where repeated introduction of new and improved antimicrobial compounds is met with equally innovative mechanisms of resistance. A classic example of this interaction is seen with the Gram-positive bacterium Staphylococcus aureus. Although initially susceptible to penicillin, introduced in the 1950s, subsequent development and spread of resistant organisms rendered the antibiotic ineffective. This was countered with the introduction of methicillin in the 1980s leading to the development of methicillin-resistant S. aureus (MRSA) which has now been followed by isolates with resistance to the historically effective antibiotic, vancomycin. Unfortunately, a survival-of-the-fittest environment ensures the perpetuation of this conflict, underscoring the importance of the continued development of novel antimicrobial agents.