CHEMISTRY THE CENTRAL SCIENCE

20 ELECTRO-CHEMISTRY

20.4 CELL POTENTIALS UNDER STAN DARD CONDITIONS

Why do electrons transfer spontaneously from a Zn atom to a Cu²⁺ ion, either directly as in Figure 20.3 or through an external circuit as in Figure 20.4? In a simple sense, we can compare the electron flow to the flow of water in a waterfall (FIGURE 20.7). Water flows spontaneously over a waterfall because of a difference in potential energy between the top of the falls and the bottom. (Section 5.1) In a similar fashion, electrons flow spontaneously through an external circuit from the anode of a voltaic cell to the cathode because of a difference in potential energy. The potential energy of electrons is higher in the anode than in the cathode. Thus, electrons flow spontaneously toward the electrode with the more positive electrical potential.

The difference in potential energy per electrical charge (the potential difference) between two electrodes is measured in volts. One volt (V) is the potential difference required to impart 1 joule (J) of energy to a charge of 1 coulomb (C):

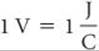
Recall that one electron has a charge of 1.60 × 10^–19 C. (Section 2.2)

The potential difference between the two electrodes of a voltaic cell is called the cell potential, denoted E_cell. Because the potential difference provides the driving force that pushes electrons through the external circuit, we also call it the electromotive (“causing electron motion”) force, or emf. Because E_cell is measured in volts, it is also commonly called the voltage of the cell.

The cell potential of any voltaic cell is positive. The magnitude of the cell potential depends on the reactions that occur at the cathode and anode, the concentrations of re-actants and products, and the temperature, which we will assume to be 25°C unless otherwise noted. In this section we focus on cells that are operated at 25°C under standard conditions. Recall from Table 19.2 that standard conditions include 1 M concentrations for reactants and products in solution and 1 atm pressure for gaseous reactants and products. The cell potential under standard conditions is called either the standard cell potential or standard emf and is denoted . For the Zn-Cu voltaic cell in Figure 20.5, for example, the standard cell potential at 25°C is +1.10 V:

Recall that the superscript ° indicates standard-state conditions. (Section 5.7)

FIGURE 20.7 Water analogy for electron flow.

GIVE IT SOME THOUGHT

If a standard cell potential is at 25 °C, is the redox reaction of the cell spontaneous?

Standard Reduction Potentials

The standard cell potential of a voltaic cell, , depends on the particular cathode and anode half-cells. We could, in principle, tabulate the standard cell potentials for all possible cathode/anode combinations. However, it is not necessary to undertake this arduous task. Rather, we can assign a standard potential to each half-cell and then use these half-cell potentials to determine . The cell potential is the difference between two half-cell potentials. By convention, the potential associated with each electrode is chosen to be the potential for reduction at that electrode. Thus, standard half-cell potentials are tabulated for reduction reactions, which means they are standard reduction potentials, denoted . The standard cell potential, , is the standard reduction potential of the cathode reaction, (cathode), minus the standard reduction potential of the anode reaction, (anode):

It is not possible to measure the standard reduction potential of a half-reaction directly. If we assign a standard reduction potential to a certain reference half-reaction, however, we can then determine the standard reduction potentials of other half-reactions relative to that reference value. The reference half-reaction is the reduction of H⁺(aq) to H₂(g) under standard conditions, which is assigned a standard reduction potential of exactly 0 V:

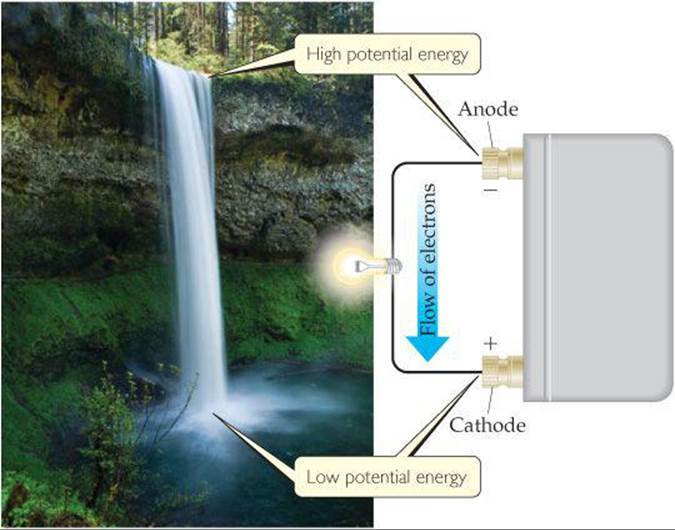
An electrode designed to produce this half-reaction is called a standard hydrogen electrode (SHE). An SHE consists of a platinum wire connected to a piece of platinum foil covered with finely divided platinum that serves as an inert surface for the reaction (FIGURE 20.8). The SHE allows the platinum to be in contact with both 1 M H⁺(aq) and a stream of hydrogen gas at 1 atm. The SHE can operate as either the anode or cathode of a cell, depending on the nature of the other electrode.

FIGURE 20.9 shows a voltaic cell using an SHE. The spontaneous reaction is the one shown in Figure 20.1, namely, oxidation of Zn and reduction of H⁺:

FIGURE 20.8 The standard hydrogen electrode (SHE) is used as a reference electrode.

GO FIGURE

Why does Na⁺ migrate into the cathode half-cell as the cell reaction proceeds?

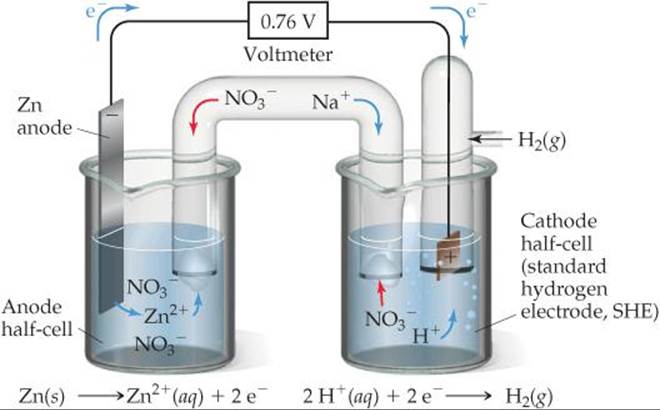
FIGURE 20.9 A voltaic cell using a standard hydrogen electrode (SHE). The anode half-cell is Zn metal in a Zn(NO₃)₂(aq) solution, and the cathode half-cell is the SHE in a HNO₃(aq) solution.

When the cell is operated under standard conditions, the cell potential is +0.76 V. By using the standard cell potential , the defined standard reduction potential of and Equation 20.8, we can determine the standard reduction potential for the Zn²⁺/Zn half-reaction:

Thus, a standard reduction potential of –0.76 V can be assigned to the reduction of Zn²⁺ to Zn:

We write the reaction as a reduction even though the Zn reaction in Figure 20.9 is an oxidation. Whenever we assign an electrical potential to a half-reaction, we write the reaction as a reduction. Half-reactions, however, are reversible, being able to operate as either reductions or oxidations. Consequently, half-reactions are sometimes written using two arrows () between reactants and products, as in equilibrium reactions.

The standard reduction potentials for other half-reactions can be determined in a fashion analogous to that used for the Zn²⁺/Zn half-reaction. TABLE 20.1 lists some standard reduction potentials; a more complete list is found in Appendix E. These standard reduction potentials, often called half-cell potentials, can be combined to calculate values for a large variety of voltaic cells.

GIVE IT SOME THOUGHT

For the half-reaction Cl₂(g) + 2 e^– → 2 Cl^–(aq), what are the standard conditions for the reactant and product?

Because electrical potential measures potential energy per electrical charge, standard reduction potentials are intensive properties. (Section 1.3) In other words, if we increase the amount of substances in a redox reaction, we increase both the energy and the charges involved, but the ratio of energy (joules) to electrical charge (coulombs) remains constant (V = J/C). Thus, changing the stoichiometric coefficient in a half-reaction does not affect the value of the standard reduction potential. For example, for the reduction of 10 mol Zn²⁺ is the same as that for the reduction of 1 mol Zn²⁺ :

TABLE 20.1 • Standard Reduction Potentials in Water at 25°C

SAMPLE EXERCISE 20.5 Calculating from

For the Zn-Cu²⁺ voltaic cell shown in Figure 20.5, we have

Given that the standard reduction potential of Zn²⁺ to Zn(s) is –0.76 V, calculate the for the reduction of Cu²⁺ to Cu:

SOLUTION

Analyze We are given and for Zn²⁺ and asked to calculate for Cu²⁺.

Plan In the voltaic cell, Zn is oxidized and is therefore the anode. Thus, the given for Zn²⁺ is (anode). Because Cu²⁺ is reduced, it is in the cathode half-cell. Thus, the unknown reduction potential for Cu²⁺ is (cathode). Knowing and (anode), we can use Equation 20.8 to solve for (cathode).

Solve

Check This standard reduction potential agrees with the one listed in Table 20.1.

Comment: The standard reduction potential for Cu²⁺ can be represented as and that for Zn²⁺ as . The subscript identifies the ion that is reduced in the reduction half-reaction.

PRACTICE EXERCISE

The standard cell potential is 1.46 V for a voltaic cell based on the following half-reactions:

Using Table 20.1, calculate for the reduction of In³⁺ to In⁺.

Answer: –0.40 V

SAMPLE EXERCISE 20.6 Calculating from

Use Table 20.1 to calculate for the voltaic cell described in Sample Exercise 20.4, which is based on the reaction

SOLUTION

Analyze We are given the equation for a redox reaction and asked to use data in Table 20.1 to calculate the standard cell potential for the associated voltaic cell.

Plan Our first step is to identify the half-reactions that occur at the cathode and anode, which we did in Sample Exercise 20.4. Then we use Table 20.1 and Equation 20.8 to calculate the standard cell potential.

Solve The half-reactions are

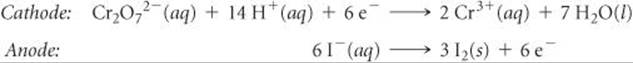
According to Table 20.1, the standard reduction potential for the reduction of Cr₂O₇^2– to Cr³⁺ is +1.33 V and the standard reduction potential for the reduction of I₂ to I^– (the reverse of the oxidation half-reaction) is +0.54 V. We use these values in Equation 20.8:

Although we must multiply the iodide half-reaction by 3 to obtain a balanced equation, we do not multiply the value by 3. As we have noted, the standard reduction potential is an intensive property and so is independent of the stoichiometric coefficients.

Check The cell potential, 0.79 V, is a positive number. As noted earlier, a voltaic cell must have a positive potential.

PRACTICE EXERCISE

Using data in Table 20.1, calculate the standard emf for a cell that employs the overall cell reaction 2 Al(s) + 3 I₂(s) → 2 Al³⁺(aq) + 6 I^–(aq).

Answer: 0.54 V – (–1.66 V) = 2.20 V

GO FIGURE

Given values for the two electrodes in a standard voltaic cell, how do you determine which electrode is the cathode?

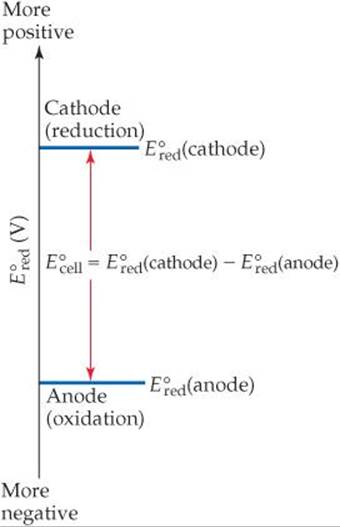
FIGURE 20.10 Graphical representation of standard cell potential of a voltaic cell.

FIGURE 20.11 Half-cell potentials and standard cell potential for the Zn-Cu voltaic cell.

For each half-cell in a voltaic cell, the standard reduction potential provides a measure of the tendency for reduction to occur: The more positive the value of , the greater the tendency for reduction under standard conditions. In any voltaic cell operating under standard conditions, the value for the reaction at the cathode is more positive than the value for the reaction at the anode. Thus, electrons flow spontaneously through the external circuit from the electrode with the more negative value of to the electrode with the more positive value of .

The fact that the standard cell potential is the difference between the standard reduction potentials of cathode and anode is illustrated graphically in FIGURE 20.10. The more positive value identifies the cathode, and the difference between the two standard reduction potentials is the standard cell potential. FIGURE 20.11 shows values for the two half-reactions in the Zn-Cu voltaic cell of Figure 20.5.

SAMPLE EXERCISE 20.7 Determining Half-Reactions at Electrodes and Calculating Cell Potentials

A voltaic cell is based on the two standard half-reactions

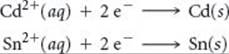
Use data in Appendix E to determine (a) which half-reaction occurs at the cathode and which occurs at the anode and (b) the standard cell potential.

SOLUTION

Analyze We have to look up for two half-reactions. We then use these values first to determine the cathode and the anode and then to calculate the standard cell potential, .

Plan The cathode will have the reduction with the more positive value, and the anode will have the less positive . To write the half-reaction at the anode, we reverse the half-reaction written for the reduction, so that the half-reaction is written as an oxidation.

Solve

(a) According to Appendix E, (Cd²⁺/Cd) = –0.403 V and (Sn²⁺/Sn) = –0.136 V. The standard reduction potential for Sn²⁺ is more positive (less negative) than that for Cd²⁺. Hence, the reduction of Sn²⁺ is the reaction that occurs at the cathode:

The anode reaction, therefore, is the loss of electrons by Cd:

(b) The cell potential is given by the difference in the standard reduction potentials at the cathode and anode (Equation 20.8):

Notice that it is unimportant that the values of both half-reactions are negative; the negative values merely indicate how these reductions compare to the reference reaction, the reduction of H⁺(aq).

Check: The cell potential is positive, as it must be for a voltaic cell.

PRACTICE EXERCISE

A voltaic cell is based on a Co²⁺/Co half-cell and an AgCl/Ag half-cell.

(a) What half-reaction occurs at the anode? (b) What is the standard cell potential?

Answers:

Strengths of Oxidizing and Reducing Agents

Table 20.1 lists half-reactions in order of decreasing tendency to undergo reduction. For example, F₂ is located at the top of the table, having the most positive value for . Thus, F₂ is the most easily reduced species in Table 20.1 and therefore the strongest oxidizing agent listed.

Among the most frequently used oxidizing agents are the halogens, O₂, and oxyanions such as MnO₄^–, Cr₂O₇^2–, and NO₃^–, whose central atoms have high positive oxidation states. As seen in Table 20.1, all these species have large positive values of and therefore easily undergo reduction.

The lower the tendency for a half-reaction to occur in one direction, the greater the tendency for it to occur in the opposite direction. Thus, the half-reaction with the most negative reduction potential in Table 20.1 is the one most easily reversed and run as an oxidation. Being at the bottom of Table 20.1, Li⁺(aq) is the most difficult species in the list to reduce and is therefore the poorest oxidizing agent listed. Although Li⁺(aq) has little tendency to gain electrons, the reverse reaction, oxidation of Li(s) to Li⁺(aq), is highly favorable. Thus, Li is the strongest reducing agent among the substances listed in Table 20.1. (Note that, because Table 20.1 lists half-reactions as reductions, only the substances on the reactant side of these equations can serve as oxidizing agents; only those on the product side can serve as reducing agents.)

Commonly used reducing agents include H₂ and the active metals, such as the alkali metals and the alkaline earth metals. Other metals whose cations have negative values—Zn and Fe, for example—are also used as reducing agents. Solutions of reducing agents are difficult to store for extended periods because of the ubiquitous presence of O₂, a good oxidizing agent.

The information contained in Table 20.1 is summarized graphically in FIGURE 20.12. The reactants in half-reactions at the top of Table 20.1 are the most readily reduced species in the table and are therefore the strongest oxidizing agents. Thus, Figure 20.12 shows F₂(g) as the strongest oxidizing agent (the position at the top of the red arrow). The products in half-reactions at the top of Table 20.1 are the most difficult to oxidize and are therefore the weakest reducing agents in the table. The reactants in half-reactions at the bottom of Table 20.1 are the most difficult to reduce and so are the weakest oxidizing agents. The products in half-reactions at the bottom of Table 20.1 are the most readily oxidized species in the table and so are the strongest reducing agents.

This inverse relationship between oxidizing and reducing strength is similar to the inverse relationship between the strengths of conjugate acids and bases. (Section 16.2 and Figure 16.3)

GO FIGURE

Why is a strong oxidizing agent easy to reduce?

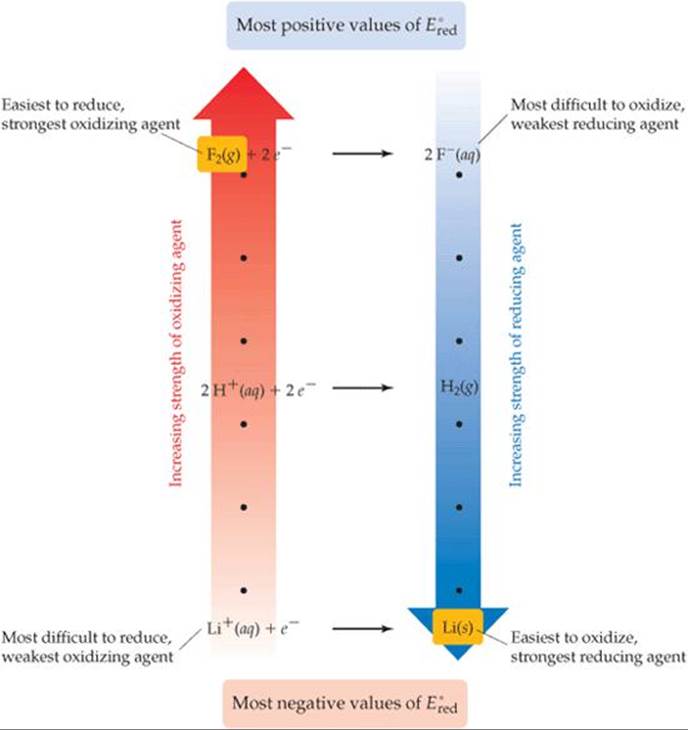
FIGURE 20.12 Relative strengths of oxidizing and reducing agents. The standard reduction potentials in Table 20.1 are related to the ability of substances to serve as oxidizing or reducing agents. Species on the left side of the half-reactions can act as oxidizing agents, and those on the right side can act as reducing agents.

SAMPLE EXERCISE 20.8 Determining Relative Strengths of Oxidizing Agents

Using Table 20.1, rank the following ions in order of increasing strength as oxidizing agents: .

SOLUTION

Analyze We are asked to rank the abilities of several ions to act as oxidizing agents.

Plan The more readily an ion is reduced (the more positive its value), the stronger it is as an oxidizing agent.

Solve From Table 20.1, we have

Because the standard reduction potential of Cr₂O₇^2– is the most positive, Cr₂O₇^2– is the strongest oxidizing agent of the three. The rank order is .

PRACTICE EXERCISE

Using Table 20.1, rank the following species from the strongest to the weakest reducing agent: I^–(aq), Fe(s), Al(s).

Answer: Al(s) > Fe(s) > I^–(aq)