CHEMISTRY THE CENTRAL SCIENCE
7 PERIODIC PROPERTIES OF THE ELEMENTS
7.3 SIZES OF ATOMS AND IONS
We often think of atoms as hard, spherical objects. According to the quantum mechanical model, however, atoms do not have sharply defined boundaries at which the electron distribution becomes zero. 
(Section 6.5) Nevertheless, we can define atomic size in several ways, based on the distances between atoms in various situations.
Imagine a collection of argon atoms in the gas phase. When two of these atoms collide with each other, they ricochet apart like colliding billiard balls. This ricocheting happens because the electron clouds of the colliding atoms cannot penetrate each other to any significant extent. The shortest distance separating the two nuclei during such collisions is twice the radii of the atoms. We call this radius the nonbonding atomic radius or the van der Waals radius (
FIGURE 7.5).
In molecules, an attractive interaction exists between any two adjacent atoms in the molecule, leading to a chemical bond between the atoms. We discuss bonding in Chapter 8. For now, we only need to realize that this attractive interaction brings the two atoms closer together than they would be in a nonbonding collision where the atoms ricochet apart. We can define an atomic radius based on the distance separating the nuclei when two atoms are bonded to each other, shown as distance d in Figure 7.5. The bonding atomic radius for any atom in a molecule is equal to half of the nucleus-to-nucleus distance d. Note from Figure 7.5 that the bonding atomic radius (also known as the covalent radius) is shorter than the nonbonding atomic radius. Unless otherwise noted, we mean the bonding atomic radius when we speak of the “size” of an atom.
Scientists have developed a variety of techniques for measuring the distances separating nuclei in molecules. From observations of these distances in many molecules, each element can be assigned a bonding atomic radius. For example, in the I2 molecule, the distance separating the nuclei is observed to be 2.66 Å, which means the bonding atomic radius of an iodine atom is (2.66 Å)/2 = 1.33 Å.* Similarly, the distance separating adjacent carbon nuclei in diamond (a three-dimensional solid network of carbon atoms) is 1.54 Å; thus, the bonding atomic radius of carbon is 0.77 Å. The bonding atomic radii of other elements can be similarly defined (
FIGURE 7.6). (For helium and neon, the bonding atomic radii must be estimated because there are no known compounds of these elements.)
Knowing atomic radii allows us to estimate bond lengths in molecules. For example, the Cl—Cl bond length in Cl2 is 1.99 Å, so a bonding atomic radius of 0.99 Å is assigned to Cl. In CCl4 the measured length of the C—Cl bond is 1.77 Å, very close to the sum (0.77 + 0.99 Å) of the bonding atomic radii of C and Cl.
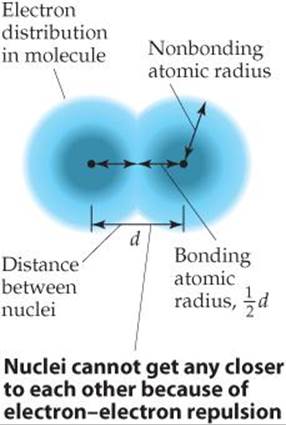
FIGURE 7.5 Distinction between nonbonding and bonding atomic radii within a molecule.
GO FIGURE
Which part of the periodic table (top/bottom, left/right) has the elements with the largest atoms?
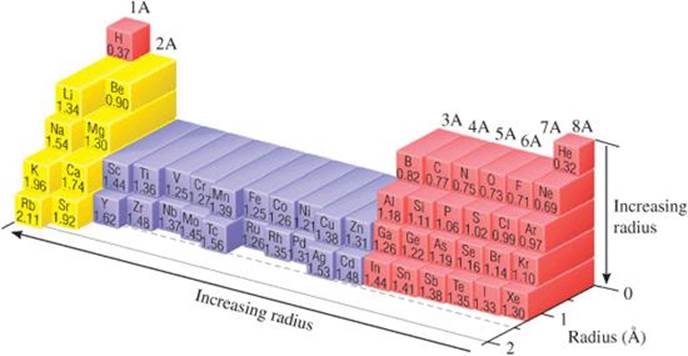
FIGURE 7.6 Trends in bonding atomic radii for periods 1 through 5.
SAMPLE EXERCISE 7.1 Bond Lengths in a Molecule
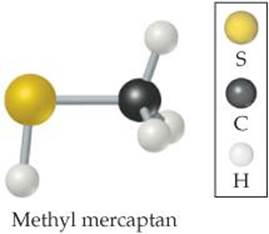
Natural gas used in home heating and cooking is odorless. Because natural gas leaks pose the danger of explosion or suffocation, various smelly substances are added to the gas to allow detection of a leak. One such substance is methyl mercaptan, CH3SH. Use Figure 7.6 to predict the lengths of the C—S, C—H, and S—H bonds in this molecule.
SOLUTION
Analyze and Plan We are given three bonds and told to use Figure 7.6 for bonding atomic radii. We will assume that each bond length is the sum of the bonding atomic radii of the two atoms involved.
Solve
Check The experimentally determined bond lengths are C—S = 1.82Å, C—H = 1.10Å, and S—H = 1.33 Å. (In general, the lengths of bonds involving hydrogen show larger deviations from the values predicted from bonding atomic radii than do bonds involving larger atoms.)
Comment Notice that our estimated bond lengths are close but not exact matches to the measured bond lengths. Bonding atomic radii must be used with some caution in estimating bond lengths.
PRACTICE EXERCISE
Using Figure 7.6, predict which is longer, the P—Br bond in PBr3 or the As—Cl bond in AsCl3.
Answer: P—Br
Periodic Trends in Atomic Radii
Figure 7.6 shows two interesting trends:
1. Within each group, bonding atomic radius tends to increase from top to bottom. This trend results primarily from the increase in the principal quantum number (n) of the outer electrons. As we go down a column, the outer electrons have a greater probability of being farther from the nucleus, causing the atomic radius to increase.
2. Within each period, bonding atomic radius tends to decrease from left to right. The major factor influencing this trend is the increase in effective nuclear charge Zeff across a period. The increasing effective nuclear charge steadily draws the valence electrons closer to the nucleus, causing the bonding atomic radius to decrease.
GIVE IT SOME THOUGHT
In Section 7.2 we said that Zeff generally increases when you move down a column of the periodic table, whereas in Chapter 6 we saw that the “size” of an orbital increases as the principal quantum number n increases. With respect to atomic radii, do these trends work together or against each other? Which effect is larger?
SAMPLE EXERCISE 6.2 Atomic Radii
Referring to a periodic table, arrange (as much as possible) the atoms 15P, 16S, 33As, and 34Se in order of increasing size. (Atomic numbers are given to help you locate the atoms quickly in the table.)
SOLUTION
Analyze and Plan We are given the chemical symbols for four elements and told to use their relative positions in the periodic table to predict the relative size of their atomic radii. We can use the two periodic trends just described to help with this problem.
Solve P and S are in the same period, with S to the right of P. Therefore, we expect the radius of S to be smaller than that of P because radii decrease as we move across a period. Likewise, the radius of Se is expected to be smaller than that of As. As is directly below P, and Se is directly below S. We expect, therefore, the radius of P to be smaller than that of As and the radius of S to be smaller than that of Se. Thus, so far we can say S < P, P < As, S < Se, Se < As. We can therefore conclude that S has the smallest radius and As has the largest radius and so can write S <? <?< As.
Our two periodic trends for atomic size do not supply enough information to allow us to determine whether P or Se (represented by the two question marks) has the larger radius, however. Going from P to Se in the periodic table, we move down (radius tends to increase) and to the right (radius tends to decrease). In Figure 7.6 we see that the radius of Se is greater than that of P. If you examine the figure carefully, you will discover that for the s- and p-block elements the increase in radius moving down a column tends to be the greater effect. There are exceptions, however.
Check From Figure 7.6, we have S(1.02Å) < P(1.06Å) < Se(1.16Å) < As (1.19 Å).
Comment Note that the trends we have just discussed are for the s- and p-block elements. Figure 7.6 shows that the transition elements do not show a regular decrease moving across a period.
PRACTICE EXERCISE
Arrange 11Na, 4Be, and 12Mg in order of increasing atomic radius.
Answer: Be < Mg < Na
Periodic Trends in Ionic Radii
Just as bonding atomic radii can be determined from interatomic distances in molecules, ionic radii can be determined from interatomic distances in ionic compounds. Like the size of an atom, the size of an ion depends on its nuclear charge, the number of electrons it possesses, and the orbitals in which the valence electrons reside. When a cation is formed from a neutral atom, electrons are removed from the occupied atomic orbitals that are the most spatially extended from the nucleus. Also, the number of electron-electron repulsions is reduced. Therefore, cations are smaller than their parent atoms (
FIGURE 7.7). The opposite is true of anions. When electrons are added to an atom to form an anion, the increased electron-electron repulsions cause the electrons to spread out more in space. Thus, anions are larger than their parent atoms.
GO FIGURE
How do cations of the same charge change in radius as you move down a column in the periodic table?
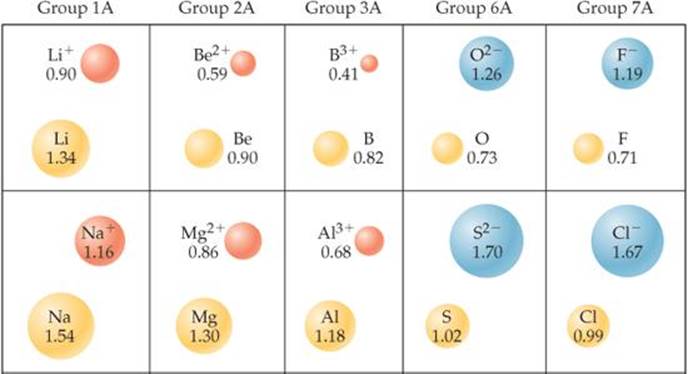
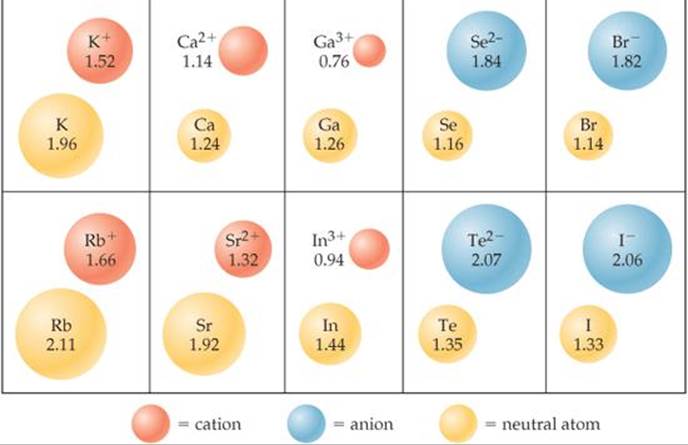
FIGURE 7.7 Cation and anion size. Radii, in angstroms, of atoms and their ions for five groups of representative elements.
For ions carrying the same charge, ionic radius increases as we move down a column in the periodic table (Figure 7.7). In other words, as the principal quantum number of the outermost occupied orbital of an ion increases, the radius of the ion increases.
SAMPLE EXERCISE 6.3 Atomic and Ionic Radii
Arrange Mg2+, Ca2+, and Ca in order of decreasing radius.
SOLUTION
Cations are smaller than their parent atoms, and so Ca2+ < Ca. Because Ca is below Mg in group 2A, Ca2+ is larger than Mg2+. Consequently, Ca > Ca2+ > Mg2+.
PRACTICE EXERCISE
Which of the following atoms and ions is largest: S2−, S, O2−?
Answer: S2−
An isoelectronic series is a group of ions all containing the same number of electrons. For example, each ion in the isoelectronic series O2−, F−, Na+, Mg2+, Al3+ has 10 electrons. In any isoelectronic series we can list the members in order of increasing atomic number; therefore, nuclear charge increases as we move through the series. Because the number of electrons remains constant, ionic radius decreases with increasing nuclear charge as the electrons are more strongly attracted to the nucleus:
Notice the positions and atomic numbers of these elements in the periodic table. The nonmetal anions precede the noble gas Ne in the table. The metal cations follow Ne. Oxygen, the largest ion in this isoelectronic series, has the lowest atomic number, 8. Aluminum, the smallest of these ions, has the highest atomic number, 13.
CHEMISTRY PUT TO WORK
Ion Movement Powers Electronics
Ionic size plays a major role in determining the properties of devices that rely on movement of ions. “Lithium ion” batteries are everywhere—cell phones, iPods, laptop computers—and so let's see how a lithium ion battery works.
A fully charged battery spontaneously produces an electric current and, therefore, power when its positive and negative electrodes are connected in an electrical circuit. The positive electrode is called the anode, and the negative electrode is called the cathode. The materials used for the electrodes in lithium ion batteries are under intense development. Currently the anode material is graphite, a form of carbon, and the cathode is most frequently LiCoO2, lithium cobalt oxide (FIGURE 7.8). Between anode and cathode is a separator, a solid material that allows lithium ions, but not electrons, to pass through.
When the battery is being charged by an external source, lithium ions migrate from the cathode to the anode where they insert between the layers of carbon atoms. Lithium ions are smaller and lighter than most other elements, which means that many can fit between the layers. When the battery discharges and its electrodes are properly connected, it is energetically favorable for the lithium ions to move from anode to cathode. In order to maintain charge balance, electrons simultaneously migrate from anode to cathode through an external circuit, thereby producing electricity.
At the cathode, lithium ions then insert in the oxide material. Again, the small size of lithium ions is an advantage. For every lithium ion that inserts into the lithium cobalt oxide cathode, a Co4+ ion is reduced to a Co3+ by an electron that has traveled through the external circuit.
The ion migration and the changes in structure that result when lithium ions enter and leave the electrode materials are complicated. Teams all over the world are trying to discover new cathode and anode materials that will easily accept and release lithium ions without falling apart over many repeated cycles. New separator materials that allow for faster lithium ion passage are also under development. Some research groups are looking at using sodium ions instead of lithium ions because sodium is far more abundant on Earth than lithium; new materials that allow sodium ion insertion and release are therefore under development. In the next decade we expect great advances in battery technology based on chemistry.
RELATED EXERCISE: 7.91
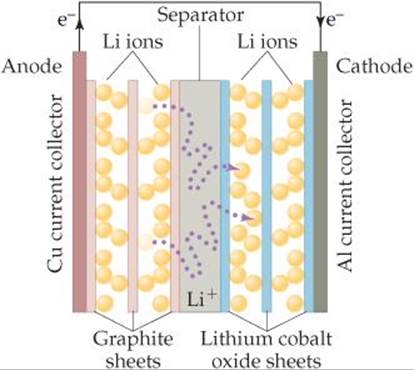
FIGURE 7.8 Schematic of a lithium ion battery.
SAMPLE EXERCISE 7.4 Ionic Radii in an Isoelectronic Series
Arrange the ions K+, Cl−, Ca2+, and S2− in order of decreasing size.
SOLUTION
This is an isoelectronic series, with all ions having 18 electrons. In such a series, size decreases as nuclear charge (atomic number) increases. The atomic numbers of the ions are S 16, Cl 17, K 19, Ca 20. Thus, the ions decrease in size in the order S2− 7 Cl− 7 K+ 7 Ca2+.
PRACTICE EXERCISE
In the isoelectronic series Rb+, Sr2+, Y3+, which ion is largest?
Answer: Rb+