Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

All bonding and molecular interaction characteristics are determined by quantum mechanics. In liquids, we deal mainly with intermolecular forces and these may be described to quite some extent via classical considerations. In this chapter, we describe the long-range electrostatic intermolecular interactions using the multipole expansion. To that we add the induction and the dispersion interactions. In this approach, short-range repulsion, due to orbital overlap, is usually treated in an empirical way. We end with a brief discussion of some often-used model potentials, together with a few remarks on hydrogen bonding and three-body interactions and the virial theorem. For further details, reference should be made to the books in the section “Further Reading” of this chapter, which have been used freely.

3.1. Preliminaries

In principle, molecules and their interactions should be described by the Schrödinger equation. As this formidable problem cannot be solved exactly we use approximate methods, and in this chapter we describe some of them for intermolecular interactions. From the Born–Oppenheimer approximation (see Section 2.4) we know that an (effective) potential energy E(r) for the motion of the nuclei with coordinates r exists. In fact, this is the potential energy employed in all of the discussions on intermolecular interactions. To emphasize the fact that E(r) acts as a potential energy, from now on, we label it as Φ(r).

Experiments together with quantum mechanics have made clear that all interaction potentials between molecules have a shape, as presented in Figure 3.1, which shows for short distances a strong repulsive part and for longer distances an attractive part of which the magnitude depends heavily on the type of bonding. We need thus to explain the origin of the attractive part and of the repulsive part.

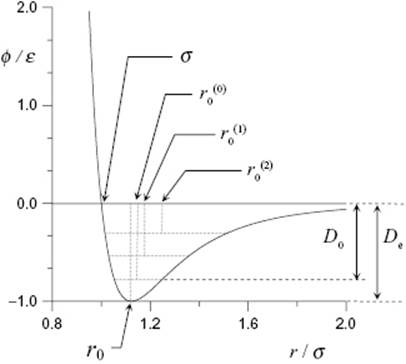
Figure 3.1 The shape of the Mie pair potential for a diatomic molecule in units of ε and σ for n = 12 and m = 6. The equilibrium distance is r₀, practically equal to for the vibrational ground state at T = 0 K. This distance increases with T due to the asymmetry of the potential and the increase in population of excited vibrational states, as indicated by and . The equilibrium energy is D_e, while the dissociation energy is D₀ = D_e−½hν (vibrational state spacing exaggerated).

The balance between the long-range, attractive interactions, collectively denoted as the van der Waals interactions Φ_vdW, and the short-ranged repulsion forces labeled as Φ_rep, determine whether a complex of molecules is stable, or not. Obviously, the total potential energy Φ is given by Φ = Φ_vdW + Φ_rep. The equilibrium distances¹⁾ r₀ are given by the solution of ∂Φ/∂r = 0, while the force constant matrix reads K = ∂²Φ/∂r∂r^′|_r=r0 (or K_ij = ∂²Φ/∂r_i∂r_j|_r=r0).

Before we discuss these interactions, let us spend a few words on the moments of a charge distribution. In molecular interactions the (continuum) charge distribution ρ(r) of the molecule is the relevant distribution, where r is the vector of coordinates. Both, nuclei and electrons contribute to ρ(r) and we assume that ρ(r) is given. Alternatively, the charge distribution is described by a (discrete) set of charges q_i at positions r_i. The zeroth moment of this distribution is a scalar and given by

(3.1)

It is essentially the charge²⁾ q of the molecule. A molecule with q = 0 is called neutral. The first moment obviously becomes

(3.2)

It is a vector called the dipole moment³⁾ with components μ_x, μ_y and μ_z. Essentially, the magnitude of the dipole moment is given by μ = |μ| = qδ, where δ is the distance between the centers of gravity of the positive and negative charges +q and −q in the molecule. The different location of these centers in the molecule renders the dipole moment a vector, leading to strong orientational forces. The ideal dipole moment is obtained by decreasing the distance δto zero, while the charge q increases in such a way that the product qδ remains μ. A molecule with μ ≠ 0 (μ = 0) is called polar (apolar). One also defines the quadrupole moment by

(3.3)

It is a symmetrical tensor with components Q_xx, Q_yy, Q_zz, Q_xy, Q_yz, and Q_zx. Higher-order moments can be defined similarly, but we will need only the charge and dipole moment. The importance of the moment expansion lies in the fact that, if a full series of moments is given, it is equivalent to the original distribution. Only the first non-zero moment is independent of the location of the origin, which is usually taken as the center of gravity of the molecule.