Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)
4. Describing Liquids: Phenomenological Behavior
4.2. Equations of State
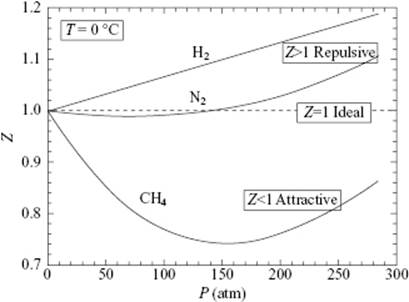
For sufficiently low temperature and a not too-high pressure, gas is described by the well-known perfect gas equation of state (EoS), given by P = nRT/V, where the pressure P is given in terms of the gas constant R, the temperature T, and the volume V for n moles of gas. All gases obey this equation in the low pressure limit, as illustrated in Figure 4.2, where the behavior of the compression factor Z = PV/RT is shown for H2, N2, and CH4. Typically, the accuracy for P according to the perfect gas EoS is ∼1% for P < 10 bar. However, for somewhat higher pressures, deviations from the perfect gas law occur and the EoS becomes material-specific (Figure 4.2; see also Figure 4.4).
Figure 4.2 Approaching the perfect gas EoS for gases as exemplified by H2, N2, and CH4. The limiting value of PV = 2271 Pa m3 mol–1 at the triple point of water, T = 273.16 K. This yields R = 8.314 Pa m3 mol–1 K–1 or 8.314 J mol–1 K–1.
An initially empirical description for a somewhat higher pressure is the “virial” equation of state. For the perfect gas the compression factor Z = 1. For a real gas, Z becomes a function of volume, which can be expanded as a power series in V−1
(4.1) ![]()
This equation is called the virial equation of state. The parameter Bj is denoted as the jth virial coefficient which is typically a function of temperature, except B1 for which obviously holds B1 = 1. Alternatively, one can expand in P
(4.2) ![]()
The coefficients Bj′ can be expressed in terms of the coefficients Bj by inverting the series. The first three coefficients then read
![]()
If only the second virial coefficient is available, one would be inclined to use Z = 1 + B2/V. However, the expression Z = 1 + B2P/RT, obtained from substituting B2′ = B2/RT in Z = 1 + B2′P, is usually much more accurate. On the contrary, if the third virial coefficient is available, the expression Z = 1 + (B2/V) + (B3/V2) is usually much more accurate than Z = 1 + B2′P + B3′P2.
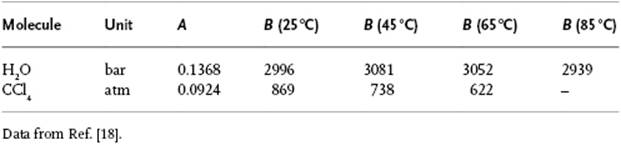
For liquids, an expression equivalent to the perfect gas EoS does not exist. A simple EoS for liquids doing remarkably well is the Tait equation [1], given by
(4.3) ![]()
Here, V0 represents the molar volume at “zero” pressure, while P0, A and B are (positive) material-specific parameters. Although there is little theoretical justification, the Tait equation in the integrated form represents the behavior of many types of liquid quite well up to pressures of about 1000 bar. Some values for the Tait parameters are given in Table 4.1. A simple empirical expression for the compressibility κT reads κT = κ0(V/V0)γ. The effect of volume on the Gibbs energy can be estimated by integrating dG = VdP − SdT at constant T, meanwhile realizing that ![]() . This leads to
. This leads to
(4.4) ![]()
Table 4.1 Parameters for Tait's isotherm for H2O and CCl4.
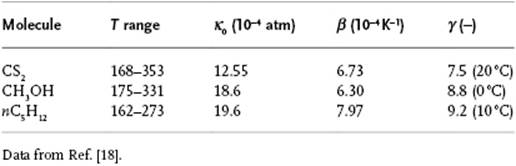
Similarly, the temperature dependence of κT can be described empirically
(4.5) ![]()
with κ0 and β constants. Some data for κ0, β and γ are given in Table 4.2. Water behaves anomalously, however, and κT passes through a minimum at ∼45 °C. For the molar volume Vsat of a saturated liquid – that is, a liquid in equilibrium with its vapor – several other empirical equations exist.
Table 4.2 Compressibility parameters for a few compounds.
It will be clear that the various equations of state describe either the behavior of the gas or the liquid. As early as 1873, van der Waals emphasized the continuity between the liquid and the gas state and advocated the EoS named after him [2]. This EoS describes liquids and gases, and for n moles it reads
(4.6) ![]()
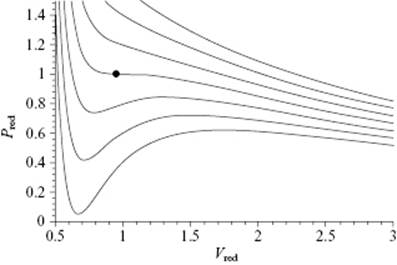
with ρ = N/V the number density. The parameters a and b are material-specific. The intuitive interpretation for a is that there is attraction between the molecules so that part of the pressure expected from the perfect gas law is reduced in overcoming the force of the intermolecular attraction. For b, one considers that a molecule is not a point mass but rather has a certain radius, so that there is a certain excluded volume given by b. Since for a rigid particle with radius σ/2 the volume that cannot be occupied by another particle is 4πσ3/3, one finds 2b = 4πσ3/3. Figure 4.3 illustrates the van der Waals (vdW) behavior. For low densities, the vdW expression reduces to the perfect gas law, but for high densities sinuous curves are obtained that represent an unstable state of affairs. The usual interpretation is that the region of the sinuous curves corresponds to a separation of the fluid into liquid and vapor, and that the equation breaks down here. Maxwell argued that a horizontal line should be inserted so as to make the areas below and above that line equal (see Chapter 16). In this way, a general resemblance to the actual isotherms of a real fluid is obtained. For mixtures it is often assumed that aij = (aiaj)1/2 and bij = (bi + bj)/2.
Figure 4.3 The van der Waals equation of state, as illustrated by isotherms in the PV-plane for Tred = 0.85, 0.90, 0.95, 1.00, 1.05, 1.10, and 1.15. The critical point is indicated by •.