Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

7.3. Hard-Sphere Results

Having indicated how to obtain the pair correlation function, the next step is to calculate the equation of state (EoS). This can be achieved in two ways: (i) to use P = −∂F/∂V, resulting in the so-called pressure equation P_P; and (ii) to use the so-called compressibility equation (see Justification 6.2), resulting in P_κ. We illustrate these expressions for the hard-sphere fluid, not to show for even a simple potential the resulting complexity, but rather in view of their importance as a reference for more realistic potentials.

Surprisingly, it appeared possible to solve the PY equation for the hard-sphere fluid using Laplace methods [13]. The result for the direct correlation function reads

(7.40)

(7.41)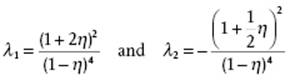

A piece-wise, rather complex analytical solution [14] for g(r) is also available.

In Chapter 6, we saw that for the pressure equation we can write Eq. (6.39)

(7.42)

We also confirmed in that chapter that, for the hard-sphere potential with e(r) = exp[−βϕ_HS(r)], the relationship d e(r)/dr = β e(r)δ(r − σ) holds. Moreover, by definition y = g/e is continuous at r = σ, so that we have for the hard-sphere fluid in the PY approximation c(r) = −y(r) if r ≤ σ and g(r) = y(r) if r ≥ σ; see Eq. (7.36). Therefore y(σ) = −c(σ) = g(σ) and we have, using, η = πσ³ρ/6,

(7.43)

Inserting the expression for c(r) the result for P_P can be shown to be

(7.44)

The other option, using the compressibility equation Eq. (7.26),

(7.45)

in combination with the solution for c(r) for hard-spheres in the PY approximation, can be shown to lead to the result for P_κ which reads

(7.46)

It will be clear that the difference between P_P and P_κ shows a lack of thermodynamic consistency, as indicated in Section 6.3. An excellent description (which means matching the simulation results within 0.3% over the whole range 0 ≤ η ≤ 0.49) of the hard-sphere EoS appears to be a weighted average of the above two results, the so-called Carnahan–Starling expression [15] given by

(7.47)

Since P/ρkT = 1 + 4ηy (Eq. 6.73), we also have

(7.48)

The reduced pressure P/ρkT according to these three equations is shown in Figure 7.3.

Figure 7.3 The EoS of a hard-sphere fluid according the pressure equation, the compressibility equation, and the Carnahan–Starling approximation for reduced density up to η = 0.494 (V/V₀ = 1.50) at which, according to simulations, the phase transition to a solid occurs.

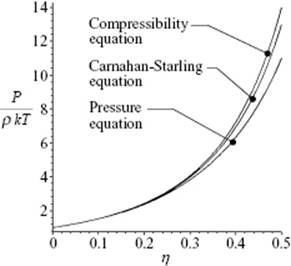
For more realistic potentials the solution of the integral equation is only possible numerically, and consequently also the EoS can be obtained only numerically. We will not pursue this topic further, but refer the reader elsewhere (e.g., Refs [6, 7]) for a more extensive comparison.

Problem 7.3

Show that, by integrating P = −∂F/∂V using the Carnahan–Starling EoS, the Helmholtz energy F of the hard-sphere liquid is given by

Problem 7.4*

Show that, using μ = −∂F/∂N and the Carnahan–Starling EoS, the chemical potential μ of the hard-sphere liquid is given by

Problem 7.5*

Show that one can obtain the Carnahan–Starling EoS by ap­proximating the coefficients in the virial expression through B₆ as expressed in reduced units by integer numbers. Try an expression such as an² + bn + c, where n is an integer, to describe the coefficients, and sum the resulting expression analytically.

Problem 7.6: The van der Waals and Carnahan–Starling fluid*

Consider the hard-sphere fluid with a reasonably dense packing. We use the pack­ing fraction η = πσ³ρ/6 = ρb/4 or using the sphere volume v₀ = (4/3)π(σ/2)³ = (πσ³)/6, η = v₀ρ. The closed-packed volume per sphere is given by σ³/2^1/2. As usual, ρ represents the number density, σ the sphere diameter, k is Boltzmann's constant, and T is the temperature. The van der Waals (vdW) EoS of the hard-sphere fluid is given by

with b a parameter, in the vdW approximation taken as b = 4v₀. The Carnahan–Starling EoS is given by Eq. (7.47).

a) The molar volume of liquid Ar at the triple point (85 K), at which equilibrium exists between gas, liquid and solid, is V_m = 28.39 cm³ mol⁻¹. If we consider Ar as a hard-sphere molecule with a diameter of 3.4 Å, what is the volume per atom v in units of volume per atom at closed-packing?

b) Show that the vdW and CS expressions to second order in ρ agree, but differ in higher order.

c) For what value of η might these expressions become infinite? Compare your answer with the value for η for Ar at the triple point. Briefly comment on the usefulness of both approaches.