Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

In Chapters 6 and 7, an outline was provided of distribution functions and the integral equation approach. This led to a rather complicated formalism from which the pair correlation, and thus the thermodynamics of liquids, can be calculated. In many cases we are not interested in the greatest accuracy achievable, but rather to understand the overall behavior of liquids. For this purpose, physical approaches based on lattice models are quite helpful as they provide excellent examples of relatively simple models in statistical thermodynamics that can be solved analytically and thus have pedagogical value. Here, we start with some preliminaries and deal thereafter with cell and hole models, in different degrees of detail. Thereafter, we discuss briefly the theory of significant liquid structures. Although today these approaches have been largely abandoned for research purposes for simple liquids, they have nevertheless the virtue to explain liquid behavior in simple terms. However, for polymers and polymeric solutions, lattice models are still actively pursued. Finally, we address scaled-particle theory.

8.1. Preliminaries

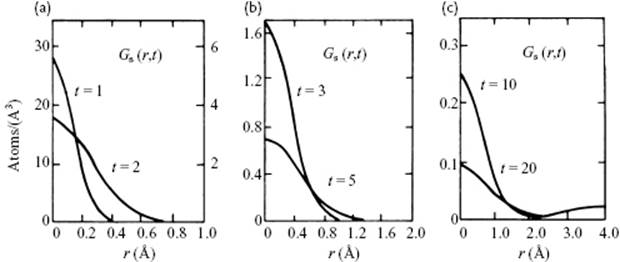
In a lattice, the atoms are located at fixed positions, whilst in an ideal gas they can be everywhere within the enclosure of the gas. In a liquid, the atoms are much less confined than in a solid, but much more so than in a gas. Consequently, their positions change more gradually and it is tempting to use, instead of the ideal gas configuration as for the virial expansion, a lattice as reference configuration. In the so-called lattice model, one assumes a lattice-like structure on average for the liquid, at least for the first coordination shell. There is some (but only some) experimental justification for this. In Figure 8.1 the self-correlation function for Ar is shown [1], describing the probability of finding a molecule that at time t = 0 was at position r = 0 at a time t at position r. This function indicates how fast, on average, a molecule moves from its reference position at time t = 0. From these graphs it can be seen that within 3 to 10 × 10⁻¹³ s, the original structure has faded away. This time corresponds to about 3 to 10 vibrations, estimating the typical vibration frequency as 10¹³ s. So, a marginal resemblance with a lattice is present. Nevertheless, the concept is useful, both for pure liquids and solutions. The existence of this temporary local structure around a reference molecule is denoted as a cell for pure liquids and as a cage (for the solute) in solutions. The molecule we have in focus (the reference molecule) is denoted as the wanderer, and the coordinating molecules constitute the wall of the cell. In this picture, each molecule thus “rattles” in a cell of which the walls are provided by the neighboring molecules. Since any molecule can be considered as either a wanderer or as a wall molecule, this constitutes a basic inconsistency, which must be accepted in order to make progress. Lattice models in which the number of cells equals the number of molecules are addressed as cell models, while models in which the number of cells is larger than the number of molecules are called hole models. In lattice models one uses the concept of free volume, that is, the space available to the motion of the center of gravity of the molecules¹⁾. The value of this can be estimated, for example, from P_vap or α_P and κ_T data (see Problems 8.3 and 8.4). Pryde [2] provided a simple introduction to lattice models, while Hirschfelder et al. [3] and Barker [4] have reviewed many details.

Figure 8.1 The self-correlation function for Ar, showing the probability of finding a particle at position r at time t that was at position r = 0 at time t = 0 for various times. The time is in units of 10⁻¹³ s.