MCAT General Chemistry Review - Steven A. Leduc 2015

MCAT Math for General Chemistry
Logarithms

15.1 THE DEFINITION OF A LOGARITHM

A logarithm (or just log, for short) is an exponent.

For example, in the equation 2³ = 8, 3 is the exponent, so 3 is the logarithm. More precisely, since 3 is the exponent that gives 8 when the base is 2,

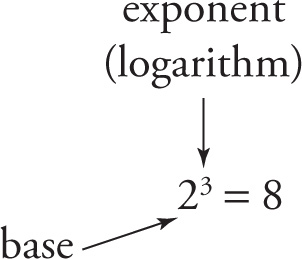
we say that the base-2 log of 8 is 3, symbolized by the equation log₂ 8 = 3.

Here’s another example: Since 10² = 100, the base-10 log of 100 is 2; that is, log₁₀ 100 = 2. The logarithm of a number to a given base is the exponent the base needs to be raised to give the number. What’s the log, base 3, of 81? It’s the exponent we’d have to raise 3 to in order to give 81. Since 3⁴ = 81, the base-3 log of 81 is 4, which we write as log₃ 81 = 4.

The exponent equation 2³ = 8 is equivalent to the log equation log₂ 8 = 3; the exponent equation 10² = 100 is equivalent to the log equation log₁₀ 100 = 2; and the exponent equation 3⁴ = 81 is equivalent to the log equation log₃ 81 = 4. For every exponent equation, b^x = y, there’s a corresponding log equation: log_b y = x, and vice versa. To help make the conversion, use the following mnemonic, called the two arrows method:

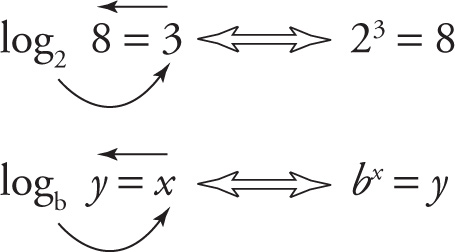
You should read the log equations with the two arrows like this:

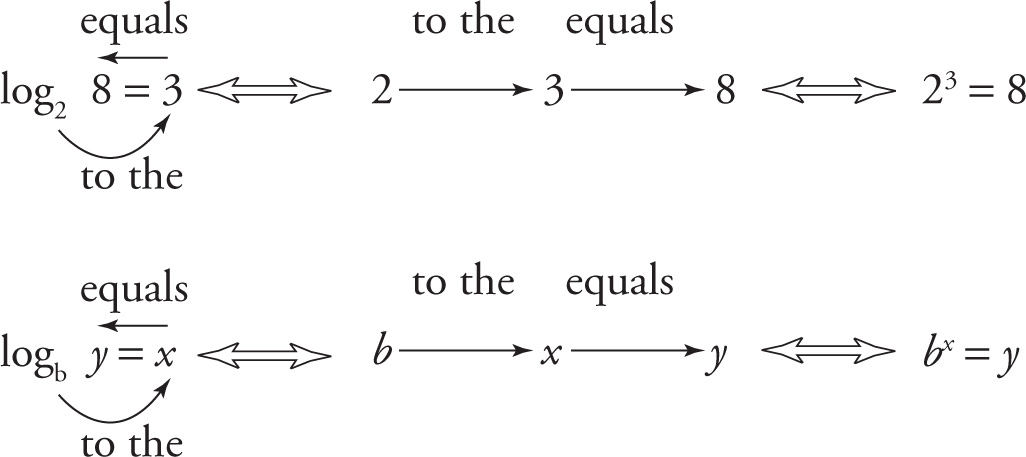
Always remember: The log is the exponent.

15.2 LAWS OF LOGARITHMS

There are only a few rules for dealing with logs that you’ll need to know, and they follow directly from the rules for exponents (given earlier, in Chapter 1). After all, logs are exponents.

In stating these rules, we will assume that in an equation like log_b y = x, the base b is a positive number that’s different from 1, and that y is positive. (Why these restrictions? Well, if b is negative, then not every number has a log. For example, log_—3 9 is 2, but what is log_—3 27? If b were 0, then only 0 would have a log; and if b were 1, then every number x could equal log₁ y if y =1, and no number x could equal log₁ y if y ≠ 1. And why must y be positive? Because if b is a positive number, then b^x [which is y] is always positive, no matter what real value we use for x. Therefore, only positive numbers have logs.)

We could also add to this list that the log of 1 is 0, but this fact just follows from the definition of a log: Since b⁰ = 1 for any allowed base b, we’ll always have log_b 1 = 0.

For the MCAT, the two most important bases are b = 10 and b = e. Base-10 logs are called common logs, and the “10” is often not written at all:

log y means log₁₀ y

The base-10 log is useful because we use a decimal number system, which is based (pun intended) on the number 10. For example, the number 273.15 means (2 × 10²) + (7 × 10¹) + (3 × 10⁰) + (1 × 10⁻¹) + (5 × 10⁻²). In physics, the formula for the decibel level of a sound uses the base-10 log. In chemistry, the base-10 log has many uses, such as finding values of the pH, pOH, pK_a, and pK_b.

Base-e logs are known as natural logs. Here, e is a particular constant, approximately equal to 2.7. This may seem like a strange number to choose as a base, but it makes calculus run smoothly—which is why it’s called the natural logarithm—because (and you don’t need to know this for the MCAT) the only numerical value of b for which the function f(x) = b^x is its own derivative is b = e = 2.71828.… Base-e logs are often used in the mathematical description of physical processes in which the rate of change of some quantity is proportional to the quantity itself; radioactive decay is a typical example. The notation “ln” (the abbreviation, in reverse, for natural logarithm) is often used to mean log_e:

ln y means log_e y

The relationship between the base-10 log and the base-e log of a given number can be expressed as ln y ≈ 2.3 log y. For example, if y = 1000 = 10³, then ln 1000 ≈ 2.3 log 1000 = 2.3 × 3 = 6.9. You may also find it useful to know the following approximate values:

Example 15-1:

a) What is log₃ 9?

b) Find log₅ (1/25).

c) Find log₄ 8.

d) What is the value of log₁₆ 4?

e) Given that log 5 ≈ 0.7, what’s log 500?

f) Given that log 2 ≈ 0.3, find log (2 × 10⁻⁶).

g) Given that log 2 ≈ 0.3 and log 3 × 0.5, find log (6 × 10²³).

Solution:

a) log₃ 9 = x is the same as 3^x = 9, from which we see that x = 2. So, log₃ 9 = 2.

b) log₅ (1/25) = x is the same as 5^x = 1/25 = 1/5² = 5⁻², so x = —2. Therefore, log₅ (1/25) = —2.

c) log₄ 8 = x is the same as 4^x = 8. Since 4^x = (2²)^x = 2^2x and 8 = 2³, the equation 4^x = 8 is the same as 2^2x = 2³, so 2x = 3, which gives x = 3/2. Therefore, log₄ 8 = 3/2.

d) log₁₆ 4 = x is the same as 16^x = 4. To find x, you might notice that the square root of 16 is 4, so 16^1/2 = 4, which means log₁₆ 4 = 1/2. Alternatively, we can write 16^x as (4²)^x = 4^2x and 4 as 4¹. Therefore, the equation 16^x = 4 is the same as 4^2x = 4¹, so 2x = 1, which gives x = 1/2.

e) log 500 = log (5 × 100) = log 5 + log 100, where we used Law 1 in the last step. Since log 100 = log 10² = 2, we find that log 500 ≈ 0.7 + 2 = 2.7.

f) log (2 × 10⁻⁶) = log 2 + log 10⁻⁶, by Law 1. Since log 10⁻⁶ = —6, we find that log (2 × 10⁻⁶) ≈ 0.3 + (—6) = —5.7.

g) log (6 × 10²³) = log 2 + log 3 + log 10²³, by Law 1. Since log 10²³ = 23, we find that log (6 × 10²³) ≈ 0.3 + 0.5 + 23 = 23.8.

Example 15-2: In each case, find y.

a) log₂ y = 5

b) log₂ y = —3

c) log y = 4

d) log y = 7.5

e) log y = —2.5

f) ln y = 3

Solution:

a) log₂ y = 5 is the same as 2⁵ = y, so y = 32.

b) log₂ y = —3 is the same as 2⁻³ = y, which gives y = 1/2³ = 1/8.

c) log y = 4 is the same as 10⁴ = y, so y = 10,000.

d) log y = 7.5 is the same as 10^7.5 = y. We’ll rewrite 7.5 as 7 + 0.5, so y =10^7+(0.5) = 10⁷ × 10^0.5. Because 10^0.5 = 10^1/2 = , which is approximately 3, we find that y ≈ 10⁷ × 3 = 3 × 10⁷.

e) log y = —2.5 is the same as 10^−2.5 = y. We’ll rewrite —2.5 as —3 + 0.5, so y = 10^−3+(0.5) = 10⁻³ × 10^0.5. Because 10^0.5 = 10^1/2 = , which is approximately 3, we have that y ≈ 10⁻³ × 3 = 0.003.

f) ln y = 3 means log_e y = 3; this is the same as y = e³ (which is about 20).

Example 15-3: The definition of the pH of an aqueous solution is

pH = —log [H₃O⁺] (or, simply, —log [H⁺])

where [H₃O⁺] is the hydronium ion concentration (in M).

Part I: Find the pH of each of the following solutions:

a) coffee, with [H₃O⁺] = 8 × 10⁻⁶ M

b) seawater, with [H₃O⁺] = 3 × 10⁻⁹ M

c) vinegar, with [H₃O⁺] = 1.3 × 10⁻³ M

Part II: Find [H₃O⁺] for each of the following pH values:

d) pH = 7

e) pH = 11.5

f) pH = 4.7

Solution:

a) pH = —log (8 × 10⁻⁶) = —[log 8 + log (10⁻⁶)] = —log 8 + 6. We can now make a quick approximation by simply noticing that log 8 is a little less than log 10; that is, log 8 is a little less than 1. Let’s say it’s 0.9. Then pH ≈ —0.9 + 6 = 5.1.

b) pH = —log (3 × 10⁻⁹) = —[log 3 + log (10⁻⁹)] = —log 3 + 9. We now make a quick approximation by simply noticing that log 3 is about 0.5 (after all, 9^0.5 is 3, so 10^0.5 is close to 3). This gives pH ≈ —0.5 + 9 = 8.5.

c) pH = —log (1.3 × 10⁻³) = —[log 1.3 + log (10⁻³)] = —log 1.3 + 3. We can now make a quick approximation by simply noticing that log 1.3 is just a little more than log 1; that is, log 1.3 is a little more than 0. Let’s say it’s 0.1. This gives pH ≈ —0.1 + 3 = 2.9.

Note 1:

We can generalize these three calculations as follows: If [H₃O⁺] = m × 10⁻ⁿ M, where 1 ≤ m < 10 and n is an integer, then the pH is between (n — 1) and n; it’s closer to (n — 1) if m > 3 and it’s closer to n if m < 3. (We use 3 as the cutoff since log 3 ≈ 0.5.)

d) If pH = 7, then —log [H₃O⁺] = 7, so log [H₃O⁺] = —7, which means [H₃O⁺] = 10⁻⁷ M.

e) If pH = 11.5, then —log [H₃O⁺] = 11.5, so log [H₃O⁺] = —11.5, which means [H₃O⁺] = 10^−11.5 = 10^(0.5)—12 = 10^0.5 × 10⁻¹² ≈ 3 × 10⁻¹² M.

f) If pH = 4.7, then —log [H₃O⁺] = 4.7, so log [H₃O⁺] = —4.7, which means [H₃O⁺] = 10^−4.7 = 10^(0.3)—5 = 10^0.3 × 10⁻⁵ ≈ 2 × 10⁻⁵ M. [10^−0.3 ≈ 2 follows from the fact that log 2 ≈ 0.3.]

Note 2:

We can generalize these last two calculations as follows: If pH = n.m, where n is an integer and m is a digit from 1 to 9, then [H₃O⁺] = y × 10⁻⁽ⁿ⁺¹⁾ M, where y is closer to 1 if m > 3 and closer to 10 if m < 3. (We take y = 5 if m = 3.)

Example 15-4: The definition of the pK_a of a weak acid is

pK_a = —log K_a

where K_a is the acid’s ionization constant.

Part I: Approximate the pK_a of each of the following acids:

a) HBrO, with K_a = 2 × 10⁻⁹

b) HNO₂, with K_a = 7 × 10⁻⁴

c) HCN, with K_a = 6 × 10⁻¹⁰

Part II: Approximate K_a for each of the following pK_a values:

d) pK_a = 12.5

e) pK_a = 2.7

f) pK_a = 9.2

Solution:

a) pK_a = —log (2 × 10⁻⁹) = —[log 2 + log (10⁻⁹)] = —log 2 + 9. We can now make a quick approximation by remembering that log 2 is about 0.3. Then pK_a = —0.3 + 9 = 8.7. Because the formula to find pK_a from K_a is exactly the same as the formula for finding pH from [H⁺], we could also make use of Note 1 in the solution to Example 15-3. If K_a = m´ × 10⁻ⁿ M, where 1 ≤ m < 10 and n is an integer, then the pK_a is between (n — 1) and n; it’s closer to (n — 1) if m > 3 and it’s closer to n if m < 3. In this case, m = 2 and n = 9, so the pK_a is between (n — 1) = 8 and n = 9. And, since 2 < 3, the pK_a will be closer to 9 (which is just what we found, since we got the value 8.7). Given a list of possible choices for the pK_a of this acid, just recognizing that it’s a little less than 9 will be sufficient.

b) With K_a = 7 × 10⁻⁴, we have m = 7 and n = 4. Therefore, the pK_a will be between (n — 1) = 3 and n = 4. Since m = 7 is greater than 3, the value of pK_a will be closer to 3 (around, say, 3.2).

c) With K_a = 6 × 10⁻¹⁰, we have m = 6 and n = 10. Therefore, the pK_a will be between (n — 1) = 9 and n = 10. Since m = 6 is greater than 3, the value of pK_a will be closer to 9 (around, say, 9.2).

d) If pK_a = 12.5, then —log K_a = 12.5, so log K_a = —12.5, which means K_a = 10^−12.5 = 10^(0.5)—13 = 10^0.5 × 10⁻¹³ ≈ 3 × 10⁻¹³. We could also make use of Note 2 in the solution to Example 15-3. If pK_a = n.m, where n is an integer and m is a digit from 1 to 9, then K_a = y × 10⁻⁽ⁿ⁺¹⁾ M, where y is closer to 1 if m > 3 and y is closer to 10 if m < 3. In this case, with pK_a = 12.5, we have n = 12 and m = 5, so the K_a value is y × 10^−(12+1) = y × 10⁻¹³, with y closer to 1 (than to 10) since m = 5 is greater than 3 (this agrees with what we found, since we calculated that K_a ≈ 3 × 10⁻¹³).

e) With pK_a = 2.7, we have n = 2 and m = 7. Therefore, the K_a value is y × 10⁻⁽²⁺¹⁾ = y × 10⁻³, with y close to 1 since m = 7 is greater than 3. We can check this as follows: If pK_a = 2.7, then —log K_a = 2.7, so log K_a = —2.7, which means K_a = 10^−2.7 = 10^(0.3)—3 = 10^0.3 × 10⁻³ ≈ 2 × 10⁻³.

f) With pK_a = 9.2, we have n = 9 and m = 2. Therefore, the K_a value is y × 10⁻⁽⁹⁺¹⁾ = y × 10⁻¹⁰, with y closer to 10 (than to 1) since m = 2 is less than 3. We can say that K_a ≈ 6 × 10⁻¹⁰.

Example 15-5:

a) If y increases by a factor of 100, what happens to log y?

b) If y decreases by a factor of 1000, what happens to log y?

c) If y increases by a factor of 30,000, what happens to log y?

d) If y is reduced by 99%, what happens to log y?

Solution:

a) If y changes to y´ = 100y, then the log increases by 2, since

log y´ = log(100y) = log 100 + log y = log 10² + log y = 2 + log y

b) If y changes to y´ = y/1000, then the log decreases by 3, since

log y´ = log(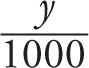) = log y − log 1000 = log y − log 10³ = log y − 3

c) If y changes to y´ = 30,000y, then the log increases by about 4.5, since

log y´ = log(30000 y) = log 3 + log 10000 + log y ≈ 0.5 + 4 + log y = 4.5 + log y

d) If y is reduced by 99%, that means we’re subtracting 0.99y from y, which leaves 0.01y = y/100. Therefore, y has decreased by a factor of 100. And if y changes to y´ = y/100, then the log decreases by 2, since

log y´ = log (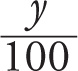) = log y − log 100 = log y − log 10² = log y − 2

Example 15-6: A radioactive substance has a half-life of 70 hours. For each of the fractions below, figure out how many hours will elapse until the amount of substance remaining is equal to the given fraction of the original amount.

a) 1/4

b) 1/8

c) 1/3

Solution:

a) After one half-life has elapsed, the amount remaining is 1/2 the original (by definition). After another half-life elapses, the amount remaining is now 1/2 of 1/2 the original amount, which is 1/4 the original amount. Therefore, a decrease to 1/4 the original amount requires 2 half-lives, which in this case is 2(70 hr) = 140 hr.

b) The fraction 1/8 is equal to 1/2 of 1/2 of 1/2; that is, 1/8 = (1/2)³. In terms of half-lives, a decrease to 1/8 the original amount requires 3 half-lives, which in this case is equal to 3(70 hr) = 210 hr. In general, a decrease to (1/2)ⁿ the original amount requires n half-lives.

c) The fraction 1/3 is not a whole-number power of 1/2, so we can’t directly apply the fact given in the italicized sentence in the solution to part (b). However, 1/3 is between 1/2 and 1/4, so the time to get to 1/3 the original amount is between 1 and 2 half-lives. Since one half-life is 70 hr, the amount of time is between 70 and 140 hours; the middle of this range (since 1/3 is roughly in the middle between 1/2 and 1/4) is about 110 hours. The most general formula for calculating the elapsed time involves a logarithm: If x < 1 is the fraction of a radioactive substance remaining after a time t has elapsed, then

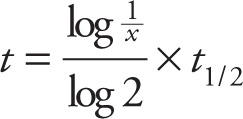
where t_1/2 is the half-life. (If you want to use this formula, remember that log 2 ≈ 0.3.)