MCAT General Chemistry Review - Alexander Stone Macnow, MD 2019-2020
The Gas Phase
Kinetic Molecular Theory
LEARNING GOALS
After Chapter 8.3, you will be able to:
· Recall the assumptions made by kinetic molecular theory
· Calculate the average speed of a gas, given its temperature
· Compare the relative speeds of two different gases at the same temperature
· Apply Graham’s law to situations involving gas effusion: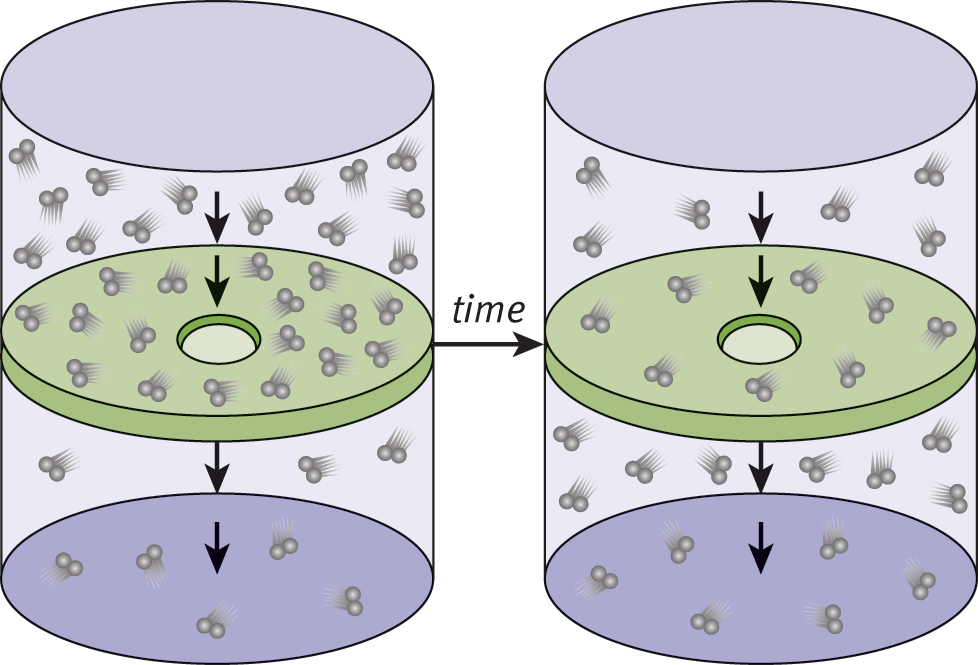
The kinetic molecular theory was developed in the second half of the 19th century, well after the laws describing gas behavior had been developed. The kinetic molecular theory was used to explain the behavior of gases, which the other laws merely described. The gas laws demonstrate that all gases show similar physical characteristics and behavior irrespective of their particular chemical identity. The behavior of real gases deviates from the ideal behavior predicted under the assumptions of this theory, but these deviations can be corrected for in calculations. The combined efforts of James Maxwell, Ludwig Boltzmann, and others led to a simple explanation of gaseous molecular behavior based on the motion of individual molecules. Like the gas laws, the kinetic molecular theory was developed in reference to ideal gases, although it can be applied with reasonable accuracy to real gases as well.
ASSUMPTIONS
To simplify the model proposed by the kinetic molecular theory, certain assumptions are made:
1. Gases are made up of particles with volumes that are negligible compared to the container volume.
2. Gas atoms or molecules exhibit no intermolecular attractions or repulsions.
3. Gas particles are in continuous, random motion, undergoing collisions with other particles and the container walls.
4. Collisions between any two gas particles (or between particles and the container walls) are elastic, meaning that there is conservation of both momentum and kinetic energy.
5. The average kinetic energy of gas particles is proportional to the absolute temperature of the gas (in kelvins), and it is the same for all gases at a given temperature, irrespective of chemical identity or atomic mass.
APPLICATIONS
It is fairly straightforward to imagine gas particles as little rubber balls bouncing off each other and off the walls of the container. Of course, rubber balls, like real gas particles, have measurable mass and volume, and not even the bounciest rubber balls will collide in a completely elastic manner. Still, this provides an apt visualization of the behaviors described by the kinetic molecular theory.
Average Molecular Speeds
According to the kinetic molecular theory of gases, the average kinetic energy of a gas particle is proportional to the absolute temperature of the gas:
![]()
Equation 8.11
where kB is the Boltzmann constant ![]() which serves as a bridge between the macroscopic and microscopic behaviors of gases (that is, as a bridge between the behavior of the gas as a whole and the individual gas molecules). This equation shows that the speed of a gas particle is related to its absolute temperature. However, because of the large number of rapidly and randomly moving gas particles, which may travel only nanometers before colliding with another particle or the container wall, the speed of an individual gas molecule is nearly impossible to define. Therefore, the speeds of gases are defined in terms of their average molecular speed. One way to define an average speed is to determine the average kinetic energy per particle and then calculate the speed to which this corresponds. The resultant quantity, known as the root-mean-square speed (urms), is given by the following equation:
which serves as a bridge between the macroscopic and microscopic behaviors of gases (that is, as a bridge between the behavior of the gas as a whole and the individual gas molecules). This equation shows that the speed of a gas particle is related to its absolute temperature. However, because of the large number of rapidly and randomly moving gas particles, which may travel only nanometers before colliding with another particle or the container wall, the speed of an individual gas molecule is nearly impossible to define. Therefore, the speeds of gases are defined in terms of their average molecular speed. One way to define an average speed is to determine the average kinetic energy per particle and then calculate the speed to which this corresponds. The resultant quantity, known as the root-mean-square speed (urms), is given by the following equation:
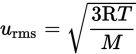
Equation 8.12
where R is the ideal gas constant, T is the temperature, and M is the molar mass.
MCAT Expertise
Understanding concepts will be much more fruitful on Test Day than memorizing all of the facts. The higher the temperature, the faster the molecules move. The larger the molecules, they slower they move.
A Maxwell—Boltzmann distribution curve shows the distribution of gas particle speeds at a given temperature. Figure 8.7 shows a distribution curve of molecular speeds at two temperatures, T1 and T2, where T2 is greater than T1. Notice that the bell-shaped curve flattens and shifts to the right as the temperature increases, indicating that at higher temperatures, more molecules are moving at higher speeds.
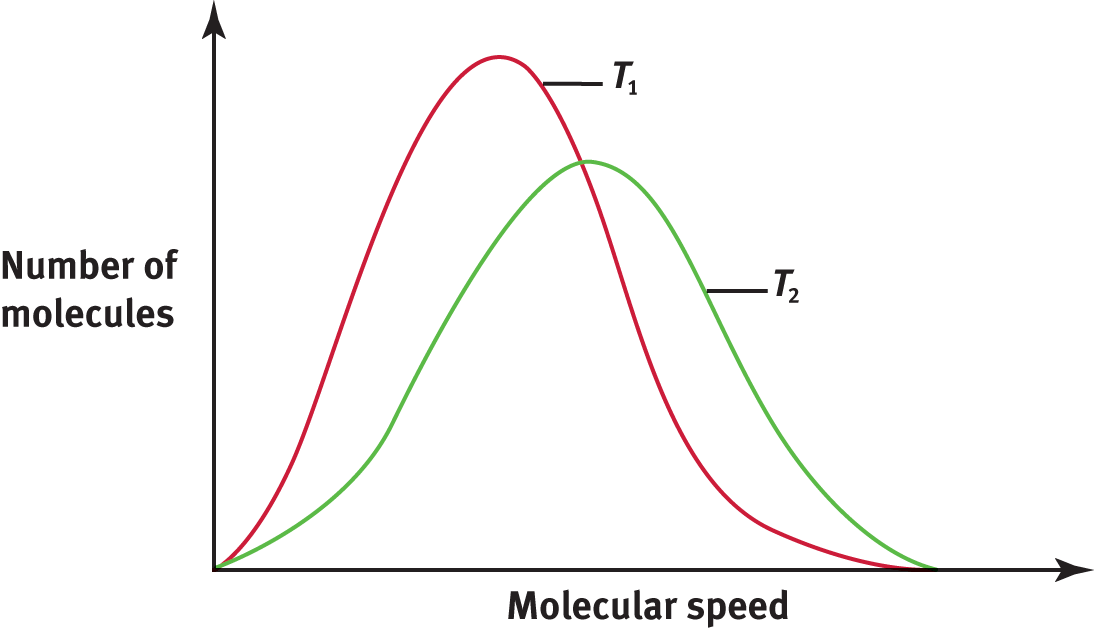 Figure 8.7. Maxwell—Boltzmann Distribution Curves of Molecular Speeds at Two Different Temperatures
Figure 8.7. Maxwell—Boltzmann Distribution Curves of Molecular Speeds at Two Different Temperatures
Example:
What is the average speed of xenon difluoride molecules at 20°C?
Solution:
The ideal gas constant ![]() should be used, and the molar mass of xenon difluoride is
should be used, and the molar mass of xenon difluoride is ![]() M must be expressed in
M must be expressed in ![]() because joules are also derived from kilograms.
because joules are also derived from kilograms.
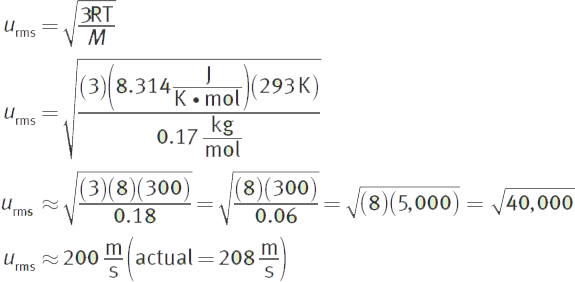
Graham’s Law of Diffusion and Effusion
The movement of molecules from high concentration to low concentration through a medium (such as air or water) is called diffusion, as shown in Figure 8.8.
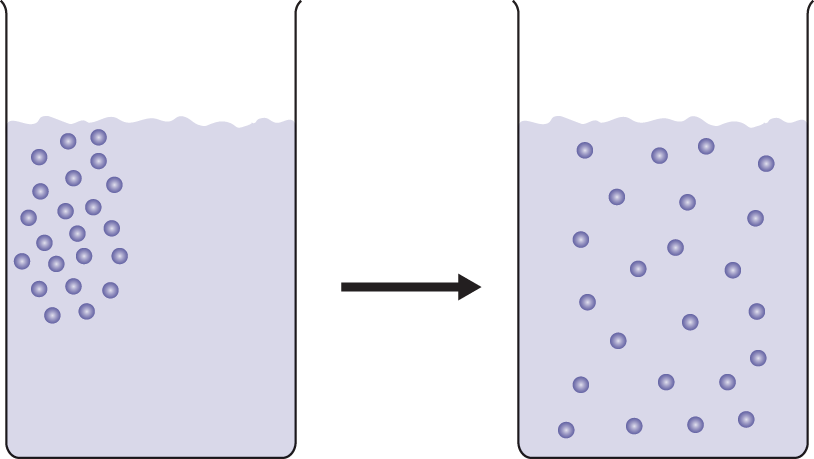 Figure 8.8. Diffusion of Solutes in a Solvent
Figure 8.8. Diffusion of Solutes in a Solvent
The kinetic molecular theory of gases predicts that heavier gases diffuse more slowly than lighter ones because of their differing average speeds, as shown in Figure 8.9. Because all gas particles have the same average kinetic energy at the same temperature, it must be true that particles with greater mass travel at a slower average speed.
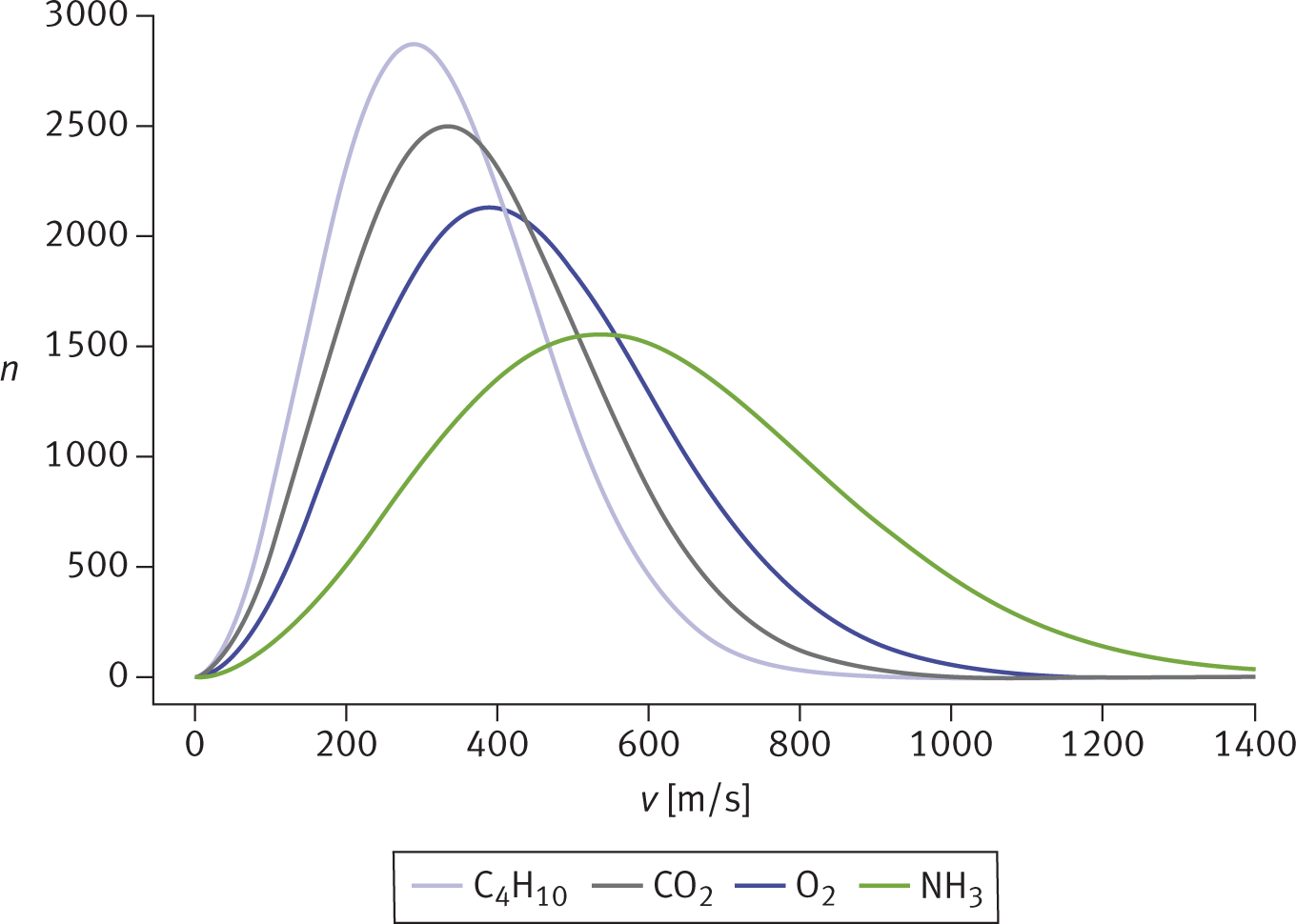 Figure 8.9. Maxwell—Boltzmann Distribution Curves of Molecular Speeds for Gases with Different Molar MassesThe more massive the gas particles, the slower their average speed.
Figure 8.9. Maxwell—Boltzmann Distribution Curves of Molecular Speeds for Gases with Different Molar MassesThe more massive the gas particles, the slower their average speed.
In 1832, Thomas Graham showed mathematically that, under isothermal and isobaric conditions, the rates at which two gases diffuse are inversely proportional to the square roots of their molar masses. This is called Graham’s law, which is written mathematically as:
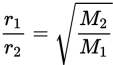
Equation 8.13
where r1 and r2 are the diffusion rates of gas 1 and gas 2, respectively, and M1 and M2 are the molar masses of gas 1 and gas 2, respectively. From this equation, we can see that a gas that has a molar mass four times that of another gas will travel half as fast as the lighter gas.
Effusion is the flow of gas particles under pressure from one compartment to another through a small opening, as shown in Figure 8.10. Graham used the kinetic molecular theory of gases to show that, for two gases at the same temperature, the rates of effusion are proportional to the average speeds. He then expressed the rates of effusion in terms of molar mass and found that the relationship is the same as that for diffusion.
 Figure 8.10. Effusion of Gas ParticlesEffusion is the flow of gas particles under pressure from one compartment to another through a small opening.
Figure 8.10. Effusion of Gas ParticlesEffusion is the flow of gas particles under pressure from one compartment to another through a small opening.
Real World
In the clinics, a pleural effusion is a condition in which fluid enters the intrapleural space through small openings in the capillaries or lymphatic vessels. This causes a pressure buildup around the lungs that hinders breathing.
Key Concept
· Diffusion—When gases mix with one another.
· Effusion—When a gas moves through a small hole under pressure.
· Both will be slower for larger molecules.
· Both conditions use the same equation.
Example:
Oxygen molecules travel at an average speed of approximately ![]() at a given temperature. Calculate the average speed of hydrogen molecules at the same temperature.
at a given temperature. Calculate the average speed of hydrogen molecules at the same temperature.
Solution:
Oxygen’s molar mass is ![]() Hydrogen’s molar mass is
Hydrogen’s molar mass is ![]() Plugging into Graham’s law, we get:
Plugging into Graham’s law, we get:
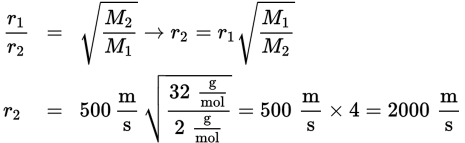
MCAT Concept Check 8.3:
Before you move on, assess your understanding of the material with these questions.
1. What are the assumptions made by the kinetic molecular theory?
2. What is the average speed of helium atoms at —173°C?
3. If neon gas travels at ![]() at a given temperature, calculate the average speed of krypton at the same temperature.
at a given temperature, calculate the average speed of krypton at the same temperature.
4. Hydrogen sulfide (H2S) has a very strong rotten egg odor. Methyl salicylate (C8H8O) has a wintergreen odor, and benzaldehyde (C7H6O) has a pleasant almond odor. If the vapors for these three substances were released at the same time from across a room, in which order would one smell the odors? Explain your answer.