Organic Chemistry I For Dummies, 2nd Edition (2014)
Part II. Hydrocarbons
Chapter 8. Drawing Alkanes
IN THIS CHAPTER
Seeing the structures of alkanes
Analyzing the conformations of alkanes
Seeing alkane reactions
In this chapter, I cover the skeletons of organic molecules — the alkanes. Alkanes are the simplest organic molecules. Because they’re the simplest of the organic molecules, they’re useful for introducing several key principles in organic chemistry, such as isomerism (molecules with the same molecular formula but different structures), conformation (the different ways atoms can flex and bend), and stereochemistry (the orientation of atoms in three-dimensional space). Also, because alkanes make up the simplest organic molecules, they’re the best place to start honing your skills in nomenclature (the rules for naming organic molecules).
Converting a Name to a Structure
It’s just as important to be able to determine the structure from a name as it is to be able to determine the name of a structure. Although English reads from left to right, the best way to read a structure’s name is from right to left. For example, if you want to draw the structure for 4-t-butyl-2,3,5-trimethylheptane, you would start by first drawing the parent chain — heptane. Heptane is seven carbons long, so you draw a seven-carbon chain (see Figure 8-1).
FIGURE 8-1: The parent chain.
Then you number the carbon chain as shown in Figure 8-2.
FIGURE 8-2: Numbering the chain.
A WORD ABOUT DRAWING AND INTERPRETING STRUCTURES
It’s easy to become confused and misled by structures written on paper, because drawn structures are simply an organic chemist’s way of conveniently representing a three-dimensional molecule on two-dimensional paper. For example, look at the following two structures and ask yourself if they refer to the same molecule or if they refer to different molecules.
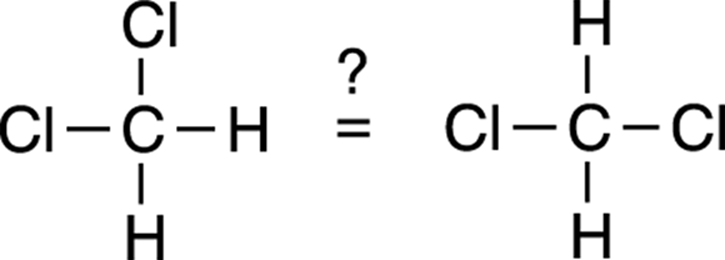
Many people would say that they’re different because they look different on paper. But both drawings are of the same molecule. The confusion results from the fact that a three-dimensional molecule is represented with a two-dimensional drawing. It looks on paper as if these molecules are flat and that each bond juts from the carbon at a 90-degree angle; in fact, the bonds are 109.5 degrees apart from each other, and the molecule has a tetrahedral geometry (refer to Chapter 2).
Likewise, it’s easy to get confused by drawings that look slightly different when they really represent the same thing. Whether you draw a straight chain with the first carbon up or the first carbon down is simply a matter of personal preference, because both represent the same molecule.
Additionally, don’t get confused by molecules not drawn in a straight chain. Straight-chain molecules can be drawn in a straight line or in a snaking fashion.
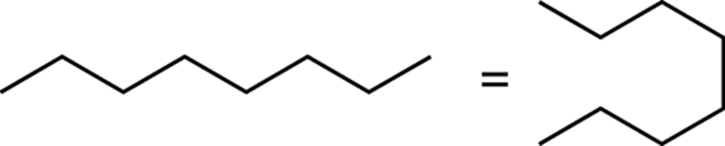
The main point I want to make is that you should be mindful of the assumptions made in these structural drawings. I also want to encourage you to use molecular models (those plastic balls and sticks that represent atoms and bonds). Especially at the beginning of the course, molecular models come in handy, allowing you to get the feel of how two-dimensional drawings relate to the actual three-dimensional structures. After you get the feel of how the drawn structures relate to the molecular models, you’ll be much less likely to be confused by the different ways that structures are drawn.
Then you stick on the substituents. Substituents can be added in any order. A t-butyl group goes on the number-four carbon (see Figure 8-3).
FIGURE 8-3: Adding a t-butyl group.
Then, methyl groups need to be plugged onto the carbons numbered two, three, and five, as shown in Figure 8-4.
FIGURE 8-4: Adding methyls.
That’s it! By reading the molecule from right to left, the structure is easily drawn from the name.
Conformation of Straight-Chain Alkanes
Carbon-carbon single bonds are capable of rotating. This allows alkanes to exist in different conformations. What are conformations? Think of a molecule in terms of your body — you can flex it and bend it. You snuggle up in bed to read a book, you sit in class to hear a lecture, and you bend to do calisthenics to get your blood flowing in the morning. All these activities put your body into different conformations. But these conformations are not of equal energy — lying down to read a book requires very little energy, sitting in class (and paying attention!) takes a bit more energy, and doing calisthenics requires a lot more energy. Now, which of these activities would you rather do? I’m guessing you’d rather be in the lower-energy conformation reading a book than in the higher-energy conformation doing calisthenics.
Similarly, alkanes can exist in different conformations — different spatial arrangements of atoms — and not all the conformations are of equal energy. And molecules — like this author — prefer to be in low-energy conformations rather than high-energy conformations.
In the following sections, I talk about the different conformations of alkanes, how you can draw alkanes in different conformations using Newman projections, and how you can predict the relative energies of conformations.
Newman! Conformational analysis and Newman projections
One of the best ways to look at different conformations of molecules (individual conformations are called conformers) is to use Newman projections. A Newman projection is a convenient way of sighting down a particular carbon-carbon bond. Figure 8-5 shows a perspective drawing of ethane and the Newman projection of the same molecule. (See Chapter 6 for more on perspective drawings.)
FIGURE 8-5: Making a Newman projection.
The solid wedges in Lewis structures indicate a bond that’s coming out of the paper, while dashed wedges indicate a bond that’s going back into the paper.
In a Newman projection, the three lines in the shape of a Y represent the three bonds of the first carbon that you’re sighting down; where the three lines connect is where the front carbon is. A circle (drawn “behind” the front carbon) represents the back carbon; the three lines coming out of the circle represent the three bonds that come off that carbon. (Note that the fourth bond for each of these carbons is the carbon-carbon bond that you’re looking down.) A Newman projection can help you analyze the rotations around a particular carbon-carbon bond.
Using Newman projections, rotating around a specific bond to reach other conformers is a fairly straightforward task. The best way to reach other conformers is to rotate just one carbon at a time — either the front carbon or the back carbon. For consistency, in this book I always hold the front of the Newman projection fixed and rotate the back carbon.
Although an infinite number of conformations exist (just rotate one of the carbons by a fraction of a degree and — voilà! — you have a different conformation), the two most important ones are the eclipsed and staggered conformations (see Figure 8-6). An eclipsed conformation results when the bonds from the front carbon and the bonds from the back carbon align with each other, and the angle between the bonds (called the dihedral angle) is 0 degrees. On the Newman projection, the eclipsed bonds are drawn a little ways apart so that the substituents on the back carbon can be seen. A staggered conformation results when the bonds from the front carbon and the bonds from the back carbon have a dihedral angle of 60 degrees. In the staggered conformation, the bonds coming off the front and back carbons are as far apart from each other as possible.
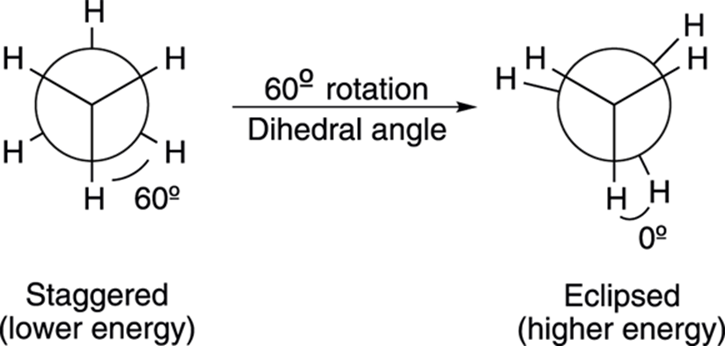
FIGURE 8-6: The staggered and eclipsed conformations in Newman projections.
When the bonds from the front carbon and back carbon are aligned in an eclipsed conformation, the electron repulsion between the bonds is higher than when the bonds are staggered and farther apart. This electron-electron repulsion between the bonds is called torsional strain. Because staggered conformations have less torsional strain than eclipsed conformations, staggered conformations are, as a general rule, more stable (that is, lower in energy) than eclipsed conformations.
Conformations of butane
The situation with butane is a bit more complicated than the situation with ethane. Figure 8-7 shows the Newman projection of butane, sighting down the bond between the second and third carbons (also known as the C2-C3 bond).
FIGURE 8-7: Sighting down the C2-C3 bond of butane.
With butane, not all eclipsed conformations are of the same energy, and not all staggered conformations are of the same energy. In Figure 8-8, I show the rotation around the C2-C3 bond in butane. In the first staggered conformation, the two methyl groups are 180 degrees apart from each other. This conformer is called the anti conformer. In the other staggered conformer, the two methyl groups flank each other. The interaction between two adjacent large groups (like methyl groups) in a staggered conformation is called a gauche interaction. Gauche interactions act to increase the energy of a conformer. Because the staggered anti conformer has no gauche interactions, it’s lower in energy than the staggered gauche conformer.
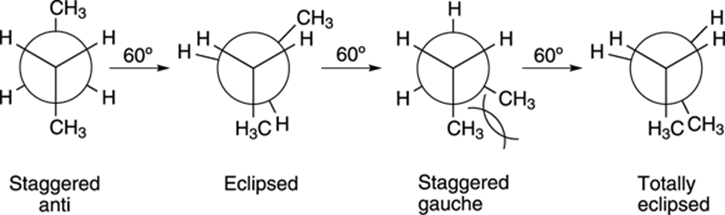
FIGURE 8-8: The conformations of butane formed by the rotation around the C2-C3 bond.
Generally, the following principle holds true: Big groups (like methyl groups) want to be as far away from each other as possible (so they don’t invade each other’s space), and conformers with the big groups far apart will be lower in energy than conformers where the big groups are near each other.
Likewise, the two eclipsed conformations are not of equal energy. In the first eclipsed conformation, the methyl groups are 120 degrees apart; in the last eclipsed conformation, the methyl groups are 0 degrees apart. This last conformer is called totally eclipsed to indicate that the two big groups are eclipsed with each other. Because the two big groups are closer together in the totally eclipsed conformer, this conformer is higher in energy than the other eclipsed conformer. The energy diagram for converting the staggered anti into the totally eclipsed conformer is given inFigure 8-9, with the x-axis representing the rotation (in degrees) and the y-axis indicating the energy (in arbitrary units).
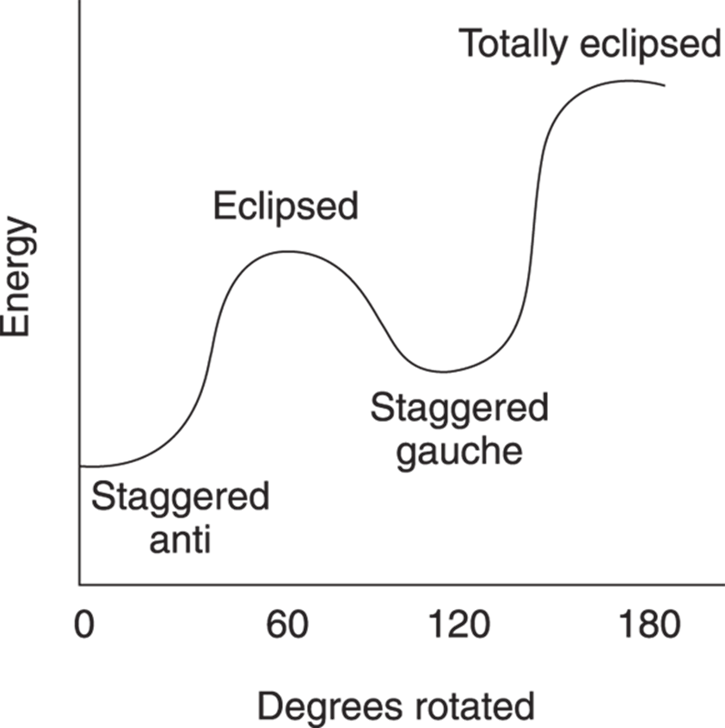
FIGURE 8-9: The energy diagram for butane conformers.
Full Circle: Cycloalkanes
Alkanes also commonly form into rings, called cycloalkanes. Cycloalkanes are named by counting the number of carbons in the ring, giving the same suffix as you would to a straight-chain alkane, and then giving the molecule the prefix cyclo–. For example, a three-carbon ring is called cyclopropane. The smallest and most common rings are shown in Figure 8-10.
FIGURE 8-10: Common cyclic alkanes.
The stereochemistry of cycloalkanes
One interesting feature of cycloalkanes is that each ring has two distinct faces. If two substituents are attached to a cycloalkane ring, they can both point off the same face, or they can point off opposite faces of the ring. Consider 1,2-dimethylcyclopentane, shown in Figure 8-11 in both the traditional perspective view and in a slanted side view — called a Haworth projection — that’s convenient for looking at the stereochemistry of rings. The two methyl groups could either point off the same face (forming an isomer called a cis stereoisomer) or point off opposite faces (forming an isomer called a trans stereoisomer). Stereoisomers are molecules that have the same connectivity of atoms but differ in the arrangement of those atoms in space.
FIGURE 8-11: The cis and trans stereoisomers of 1,2- dimethylcyclopentane.
Conformations of cyclohexane
Although cyclohexane is typically drawn as if it were flat, in reality the structure is not flat at all. Most of the time, the structure exists in what is called the chair conformation. This conformation is called the chair because it looks (sort of) like a reclining lounge chair (see Figure 8-12). Other conformations for cyclohexane do exist — and they include the boat, half-chair, and twist-boat conformations — but the most important conformation is the chair because this conformation is typically the most stable conformation.
FIGURE 8-12: The chair conformation of cyclohexane.
Drawing chairs
Many students find that drawing chairs can be somewhat difficult at first, but mastering the correct drawing of this conformation is essential for your success in orgo. To begin, start by drawing two lines that are parallel to each other but not perfectly horizontal, as shown in Figure 8-13. Next, add a downward-pointing V tip to one end (this is the tail of the chair). Finally, add an upward-pointing V tip to the other end (this is the nose of the chair).
FIGURE 8-13: The steps involved in drawing the chair conformation of cyclohexane.
Adding hydrogens to a chair
A cyclohexane chair contains two kinds of hydrogens — axial hydrogens and equatorial hydrogens. Axial hydrogens are those hydrogens that stick straight up or straight down parallel to an imaginary axis through the chair; equatorial hydrogens are hydrogens that stick out along the equator of the chair (see Figure 8-14).
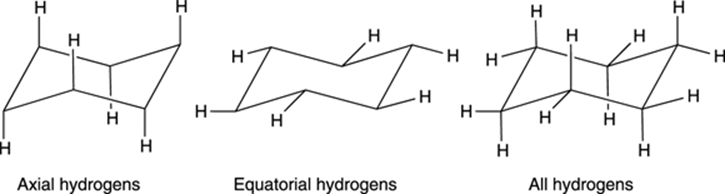
FIGURE 8-14: The axial and equatorial hydrogens on cyclohexane.
In drawing the hydrogens on a chair cyclohexane, it’s often easiest to draw the axial hydrogens first. At any point on the chair that sticks up, put the axial hydrogen sticking straight up; at any point on the chair that sticks down, draw the axial hydrogen straight down. After the axial hydrogens are drawn, adding in the equatorial hydrogens around the equator of the chair is a fairly straightforward task.
Flipping the chair
At room temperature, cyclohexane doesn’t stay in one-chair conformation, but rapidly interconverts into an alternative chair conformation with a ring flip (shown in Figure 8-15). With the chair on the left of the figure, the nose of the cyclohexane chair goes down, and the tail of the cyclohexane goes up to make the new chair cyclohexane conformer. With a ring flip, all hydrogens that were originally axial become equatorial, and all hydrogens that were equatorial become axial. It’s a good idea to get out your molecular models and try this ring flip yourself, so you can see it in three dimensions.
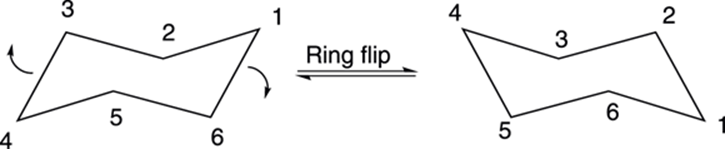
FIGURE 8-15: The ring flip of cyclohexane.
With unsubstituted cyclohexane (a cyclohexane that has only hydrogens attached to it), undergoing a ring flip doesn’t change the molecule. With substituted cyclohexanes, however, the two chair conformers may not be identical. For example, isopropylcyclohexane is shown in Figure 8-16. One chair conformer puts the isopropyl group in the axial position. After undergoing a ring flip, the isopropyl becomes equatorial.
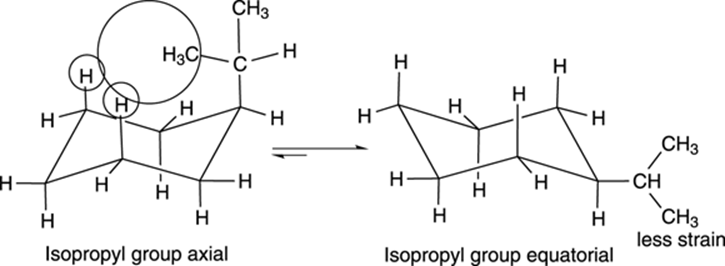
FIGURE 8-16: The chair conformers of isopropylcyclohexane.
Ring flips change all axial positions to equatorial and all equatorial positions to axial.
These two conformers are not identical, and they don’t have the same energy. When a large group is axial, the large group invades the space of the hydrogens on carbons two positions away, introducing 1,3-diaxial strain. This interaction increases the energy of the axial conformer. Therefore, as a rule, large groups prefer to be equatorial because this conformation has no 1,3-diaxial strain — the right-pointing arrow is longer, indicating the direction of the equilibrium favors the more stable chair conformation (see Figure 8-16).
Don’t confuse conformation with configuration. A cis configuration (a molecule with substituents pointing off the same face of the ring) or trans configuration (a molecule with substituents pointing off opposite faces of the ring) doesn’t change by changing the conformation. For example, a ring flip of a cyclohexane will not change a cis configuration to a trans configuration, because after the flip the substituents will still be pointing off the same face (for a cis configuration) or off opposite faces (for a trans configuration). The only way to change the configuration is by chemical reactions that make and break bonds.
Problem Solving: Drawing the Most Stable Chair Conformation
The first step in drawing the most stable conformation of cyclohexane is to determine — based on whether the substituents are cis or trans to one another, and based on where they’re located on the ring — what the choices of axial and equatorial positions are for the substituents. A handy way of determining the substitution alternatives is to use the Haworth projection in Figure 8-17. This projection is easy to make — simply start at some position on the ring and alternate axial (a) and equatorial (e) from carbon to carbon, and from top to bottom. This projection will tell you what the two options for the two-chair conformations are.
FIGURE 8-17: The Haworth projection.
For example, if you were asked to draw the most stable conformation of cis-1,3-dimethylcyclohexane, both substituents could be on the top of the ring or both could be on the bottom of the ring, as shown in Figure 8-18. (Recall that cis means that both substituents are on the same side of the ring.) As the figure shows, to get the cis stereochemistry, either both of the substituents could be equatorial (both e) or both could be axial (both a).
FIGURE 8-18: The possible positions of cis substituents in positions 1 and 3 on cyclohexane.
Putting large groups in the equatorial position to eliminate 1,3-diaxial strain is energetically favorable.
Because large groups prefer to be equatorial, the most stable conformer for cis-1,3-dimethylcyclohexane is the diequatorial conformer, shown in Figure 8-19. The diaxial conformer would be higher in energy.
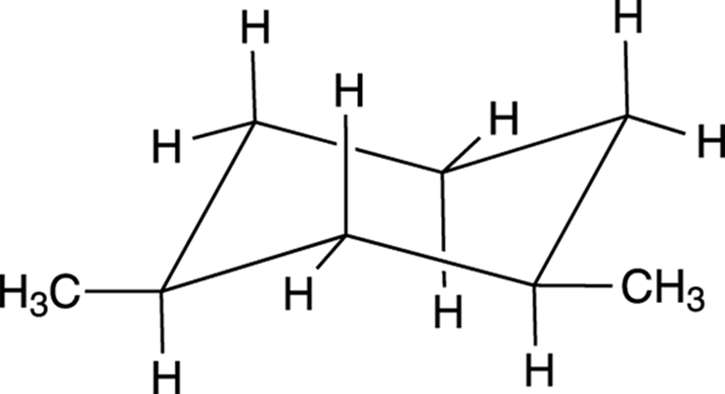
FIGURE 8-19: The diequatorial conformation of cis-1,3 -dimethylcyclohexane.
If cyclohexane has two substituents and one has to be placed axial and one equatorial (as is the case in trans-1,2-disubstituted cyclohexanes), the lowest-energy conformation will be the one in which the bigger group goes in the equatorial position and the smaller group goes in the axial position.
Reacting Alkanes: Free-Radical Halogenation
Because alkanes are essentially inert under most conditions, virtually the only reaction of alkanes that you see is the free-radical halogenation reaction. This reaction is often the first reaction that you encounter in organic chemistry.
The chlorination of methane is shown in Figure 8-20. In this reaction, a chlorine atom is substituted for a methane hydrogen.
FIGURE 8-20: The chlorination of methane.
One feature that’s interesting about this chlorination reaction is that the reaction is photochemical: Instead of using heat to start the reaction, the reaction uses light (abbreviated hν)! The reaction proceeds in three stages — initiation, propagation, and termination.
Getting things started: Initiation
In the initiation step, light is shone on the reaction and the radiation is absorbed by the chlorine (Cl2). The light provides enough energy for the married chlorines to divorce — that is, for the chlorine-chlorine bond to break apart to form two chloride radicals, as shown in Figure 8-21. (Recall that free radicals are compounds that contain unpaired electrons.) This kind of bond dissociation is called homolytic cleavage, because the bond breaks symmetrically — one electron from the bond goes to one side, and the other electron goes to the other side, just as half of the shared property goes to each person in a divorce (theoretically). Note that you use one-headed fishhook arrows to show the movement of only one electron. See Chapter 3 for more on using arrows in organic chemistry.
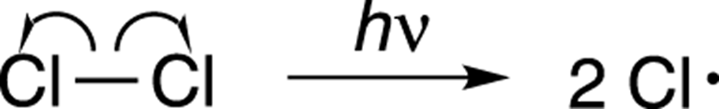
FIGURE 8-21: The initiation step.
Keeping the reaction going: Propagation
After the reaction has been initiated by forming the chlorine radicals, the reaction proceeds to the propagation steps (see Figure 8-22). A chlorine radical is unstable because the chlorine atom only has seven valence electrons, one electron short of having its valence octet completely full. To fill its valence octet, a chlorine radical then plucks a hydrogen atom (not a proton) from the methane to make hydrochloric acid plus the methyl radical. Now, however, the methyl radical is one electron short of completing its octet. So, the methyl radical then attacks another molecule of chlorine to make chloromethane plus another chlorine radical.
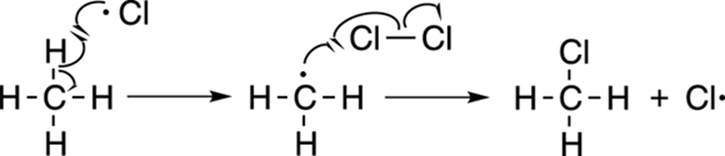
FIGURE 8-22: The propagation steps.
You’re fired: Termination steps
Because this reaction generates chlorine radicals as a byproduct, the reaction is called a chain reaction. In a chain reaction, the reactive species (in this case, the chlorine radical) is regenerated by the reaction. If not for the termination steps, this reaction could theoretically continue until all the starting materials were consumed. Termination steps are reactions that remove the reactive species without generating new ones. Any of the radical couplings shown in Figure 8-23 are considered termination steps because they remove the reactive species (the free radicals) from the reaction without replacing them.
FIGURE 8-23: The termination steps for the chlorination of methane.
When solving multistep synthesis problems (see Appendix A), you’re often given an alkane-starting material. One of the best ways to get your foot in the door (often the only way) as far as putting a functional group on the molecule is to brominate (or chlorinate) the alkane using this free-radical reaction.
What about the chlorination of larger molecules that have different kinds of hydrogens? In methane only one kind of hydrogen is available to be pulled off — and so only one possible product can be made — but in larger molecules, several products can be formed. For example, butane (see Figure 8-24) has two types of hydrogen. Hydrogens are classified according to the substitution of the carbon to which they’re attached. Hydrogens attached to primary carbons (or carbons bonded to only one other carbon) are called primary hydrogens, hydrogens attached to secondary carbons (or carbons bonded to two other carbons) are called secondary hydrogens, and so on. Butane has two types of hydrogens — primary hydrogens (1 degree) and secondary hydrogens (2 degrees).
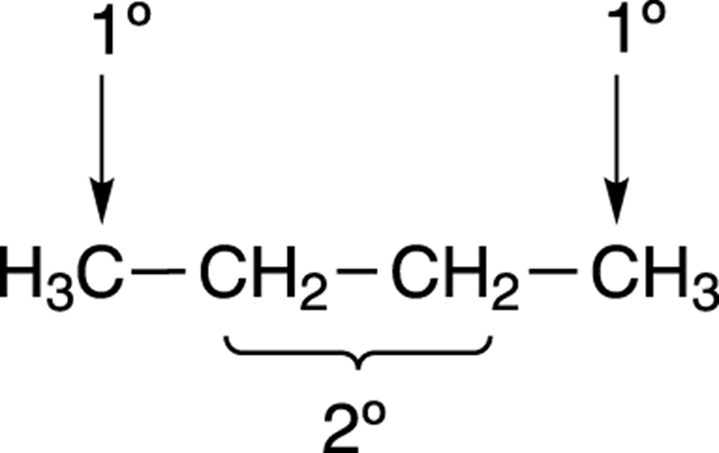
FIGURE 8-24: The primary and secondary hydrogens on butane.
The chlorination of butane selectively forms the product that results from the chloride radical abstracting a secondary hydrogen to make the secondary radical, as shown in Figure 8-25.
FIGURE 8-25: The chlorination of butane.
To see why this is so, you need to consider the stabilities of free radicals. Radicals are more stable when they rest on more highly substituted carbons, as Figure 8-26 shows. Thus, you preferentially get chlorine substitution on the more highly substituted carbon atom.
FIGURE 8-26: The relative stability of free radicals.
Selectivity of chlorination and bromination
The bromination of alkanes occurs in the same fashion as the chlorination of alkanes, except that Br2 is used in the reaction instead of Cl2. One difference between the chlorination and bromination of alkanes is that bromide radicals are more selective for hydrogen on more substituted carbons than chloride radicals are.
Chlorine radicals are less stable than bromine radicals and, thus, have only modest selectivity for reacting with hydrogens on more substituted carbons, reacting many times with any hydrogen it bumps into. Bromine radicals, however, are more stable than chlorine radicals and, thus, are happier to wait until they bump into a hydrogen on a more highly substituted carbon before reacting.