Physical Chemistry Essentials - Hofmann A. 2018
Mixtures and Phases
3.1 Why Do or Don’t Things Mix
In every-day life, we frequently encounter systems that consist of more than one component and thus represent mixtures. An important fundamental question in this context is whether two different components will spontaneously mix.
3.1.1 Gases
Experience tells us that two gases contained in the same physical container will inter-mix. Since all spontaneous processes (at constant pressure) must be accompanied by a negative change of the Gibbs free energy (Eq. 2.50), we can assess the every-day experience by thermodynamic means.
The Gibbs free energy change for the mixing process can be calculated as per:
![]()
(3.1)
The Gibbs free energies for the initial state of the system is given by the sum of the chemical potentials of each of the components that are about to mix, A and B, multiplied by their respective molar amounts n A and n B. The chemical potential of a gas at a pressure p was introduced with Eq. 2.67, and μ— indicates represents the chemical potential under standard conditions:
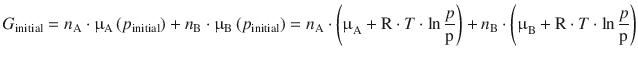
When the mixing process starts (i.e. in the initial state), we are releasing two gases A and B into a container with an atmosphere of pressure p. In the final state, when the inter-mixing of the gases is complete, we know that each component can be described by its partial pressure, p A and p B (see page 28). The chemical potential for each component can thus be calculated by using the partial pressures, and one thus obtains for the Gibbs free energy in the final state:
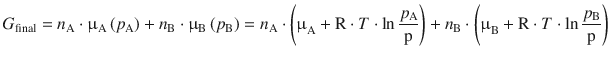
Both expressions can now be used to substitute in Eq. 3.1:
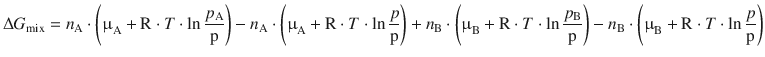
The molar amounts n A and n B, the chemical potentials in the standard state, as well as R and T are all constants and therefore separated from the unknown parameters p, p A and p B:
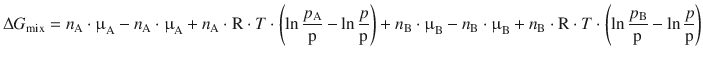
We see that the above expression can be simplified since some terms cancel:
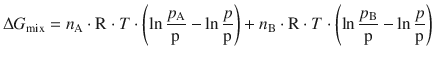
With the logarithm rule of ![]() (see Appendix A.1.2) one obtains:
(see Appendix A.1.2) one obtains:
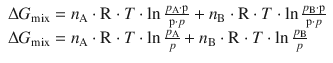
As we have introduced earlier (Eq. 2.75), the quotient of partial pressure and total pressure yields the mole fraction x, when dealing with gases. The above equation can thus be re-written in terms of mole fractions x A and x B:
![]()
The molar amounts of A and B, n A and n B, are related to the mole fractions via the total molar amount of compounds in the system:
![]()
Therefore we arrive at:
![]()
(3.2)
Since x A and x B are positive numbers between 0 and 1, it becomes clear that lnx A and lnx B are negative numbers, since any logarithmic function is negative between 0 and 1 (Fig. 3.1). With (n ⋅ R ⋅ T) yielding a positive value, we can then conclude that ΔG mix from Eq. 3.2 will always deliver a negative value. Since all processes with ΔG < 0 are spontaneous processes, the mixing of two gases is a spontaneously occurring process!
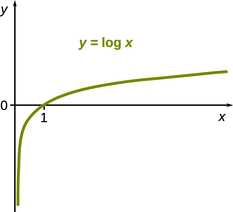
Fig. 3.1
Any logarithmic function results in negative values between 0 and 1
Considering that the Gibbs free energy change at constant pressure and constant temperature is composed of enthalpic and entropic changes as per:
![]()
(2.42)
we can conclude that the mixing two ideal gases is a purely entropic effect, since there is no enthalpy change (ΔH = 0) when two ideal gases intermix. This follows from the requirement of the gas being ideal; in the ideal gas there are no intermolecular forces between the molecules.
In contrast, in real gases inter-molecular interactions do occur and there is therefore a change of enthalpy upon mixing (ΔH ≠ 0), due to intermolecular forces between molecules. It also needs to be considered that ΔH and ΔS depend on p and T. However, the Gibbs free energy change for the inter-mixing of real gases is still generally negative.
3.1.2 Liquids
A similar approach can be taken, when considering the mixing of two liquids. As in the previous section, we establish the Gibbs free energy of the system before mixing occurs. This can be expressed as the sum of the chemical potentials of the pure liquids (indicated by the asterisk ’*’), multiplied with the respective molar amounts of each liquid in the system (since the chemical potential is the Gibbs free energy per 1 mol of substance):
![]()
When applying Eq. 2.67 to liquid systems, we appreciate that the chemical potential of a liquid at any concentration can be expressed with reference to the chemical potential in its pure state (’*’) by adjusting for the concentration of the liquid with the term R ⋅ T ⋅ ln x, where x is the mole fraction of the liquid:
![]()
(3.3)
The final state of the liquid mixture is attained when both liquids are present in their respective concentrations, expressed as mole fractions x A and x B. With Eq. 3.3 we thus obtain:
![]()
and can now proceed to calculate the change in the Gibbs free energy during the mixing process:
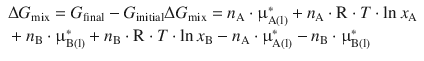
Since several terms cancel, this simplifies to:
![]()
We then express the individual molar amounts n A and n B as mole fractions x A and x B (and thus with respect to the total molar amount n in the system):
![]()
which yields for the Gibbs free energy change of the mixing process:
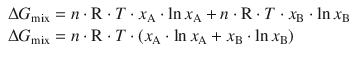
(3.4)
As we have discussed in the previous section, due to the mole fractions x A and x B taking values between 0 and 1, Eq. 3.4 we always deliver a negative value for the Gibbs free energy change, and the mixing of two liquids should thus always occur spontaneously. However, as in the case of gases, this is only true for ideal liquids, i.e. such that do not possess any intermolecular forces between molecules. With
![]()
(2.42)
we can then conclude that in ideal solutions, at constant temperature and constant pressure, there is no enthalpy change (ΔH = 0) and the mixing of ideally behaving liquids is thus a purely entropic effect: ΔG mix = − T ⋅ ΔS.
In contrast to gases, non-ideal effects are a lot more common in liquids, and therefore we frequently need to consider changes in ΔH due to intermolecular forces, which differ when comparing interactions between A—A, B—B and A—B. A positive change of the enthalpy during the mixing (ΔH > 0) of two liquids is therefore possible and may eventually exceed the entropic effect. The Gibbs free energy of mixing of non-ideal liquids may thus be positive or negative; this will determine whether or not the liquids mix.