Physical Chemistry Essentials - Hofmann A. 2018
Quantum Mechanics of Simple Systems
9.4 Tunnelling
In Sect. 9.1.3, we saw that the probability to find a particle outside a box with walls of a finite potential is non-zero (Fig. 9.4), i.e. it may exist outside the box. A similar observation has been made in the previous section when discussing the harmonic oscillator (Fig. 9.10). Therefore, the question arises as to whether and how a particle may be able to tunnel through a sufficiently thin potential barrier, despite its energy E being lower than the potential energy E pot = V 0.
The situation is illustrated in Fig. 9.11. Three regions need to be considered:
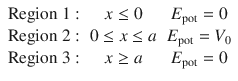
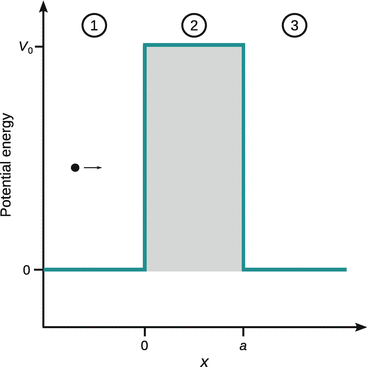
Fig. 9.11
Illustration of the tunnelling through a sufficiently thin potential wall
For regions 1 and 3, the Schrödinger equation is thus:
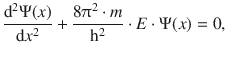
and for region 2, it reads:
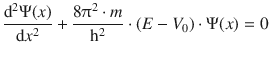
For both equations, we can define a constant k that comprises of the factor before Ψ(x), i.e.:
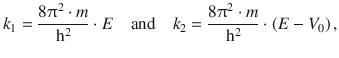
which leads to the following solutions for the wave functions in the three regions 1—3:
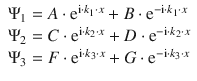
In all of the three above equations, the first term describes particles moving from the left to the right (see Fig. 9.11), and the second term describes particles moving from the right to the left. In regions 1 and 2 particles originally moving from the left to the right will be partially reflected on the potential walls, which leads to some particles moving from the right to left in those regions. Therefore, the coefficients B and D need to be non-zero. In region 3, if particles made it through to that region, they will keep on moving to the right and not return, so the coefficient G is zero.
Importantly though, the fraction of particles which made it from region 1 to region 3 depends on the ratio of the coefficients F and A. This ratio is called the transmission coefficient T:
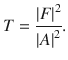
(9.40)
In order to determine the constants A, B, C, D and F, we need to consider that the overall wave function Ψ (and its derivatives) need to be continuous. Without discussing this mathematical derivation in detail, we appreciate that the following result is obtained for the transmission coefficient:
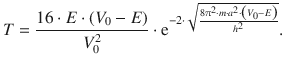
(9.41)
This equation demonstrates that the tunnelling probability, given by the transmission coefficient T, mainly depends on the energy difference (E—V 0) as well as the width a of the potential barrier. For a given energy E of the particle, the transmission coefficient decreases with increasing height of the potential barrier (V 0). The transmission coefficient further decreases, if the width a, i.e. the barrier thickness, increases.