Physical Chemistry Essentials - Hofmann A. 2018

Quantum Theory of Atoms
10.3 Multi-Electron Atoms

10.3.1 The Schrödinger Equation for Multi-Electron Atoms

We have seen in the previous sections that the Schrödinger equation can be solved for the hydrogen atom, which consists of a positively charged nucleus and one electron. The same is true for any one-electron species, such as H₂ ⁺, He⁺, Li²⁺, Be³⁺, etc. However, atoms that possess more than one electron present additional challenges such that the Schrödinger equation can no longer be solved in an exact fashion.

If more than one electron is present, each electron experiences an attractive force by the nucleus, but a repelling force by all other electrons. The potential energy in the Schrödinger equation therefore not only depends on the distance of an electron from the nucleus, but also from the distance to all other electrons. As this requires consideration of all individual interactions between the electrons, it becomes impossible to determine an exact solution of the Schrödinger equation.

An approximation suggested by Douglas Hartree in 1927 replaces the individual inter-electronic interactions by the interaction of an electron with a mean field which may be assumed to be of spherical symmetry. The non-linear equations evolving from this approach are solved in an iterative fashion, and the methodology has become known as the self-consistent field method or Hartree-Fock method. Even though more accurate methods have been developed since, the Hartree-Fock method remains the starting point for almost all methods that describe multi-electron systems. Its inherent shortcomings stem from that fact that the mean field of other electrons are assumed to be of spherical symmetry. However, it has become apparent that especially for heavy atoms those errors are indeed very small.

10.3.2 Electronic Configuration of Atoms

We have seen in the previous discussion of the hydrogen atom, that the allowed energy levels can be calculated and only depend on the principal quantum number n (Eq. 10.9), such that the atomic orbitals can be arranged in the order of increasing energy:

For multi-electron systems, calculations show that the order differs from that of the one-electron system above; specifically:

The reason for this difference is in the fact that electrons for example in the 2s orbital are closer to the nucleus than those in the 2p orbital, given the spherical distribution of the former (see Sect. 10.1.3). The 2s electrons thus experience a stronger attractive force by the nucleus than the 2p electrons which are shielded (by the 2s electrons). The shielding makes it a less stable arrangement and hence leads to a higher potential energy. When arranging the individual atomic orbitals relative to each other on an energy scale, one arrives at scheme as illustrated in Fig. 10.10.

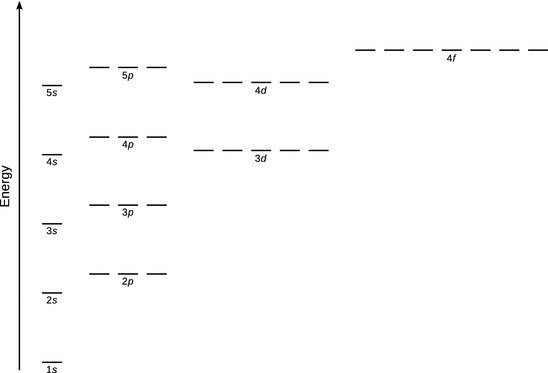
Fig. 10.10

Relative energetic levels of atomic orbitals in multi-electron systems

The order number Z of the periodic system indicates the number of protons in the nucleus and hence the number of positive charges of an atom that need to be balanced by the surrounding electrons (when considering an element). Clearly, when populating the scheme in Fig. 10.10 with electrons for atomic hydrogen, the one electron needs to go into the lowest lying orbital (1s). When considering the helium atom, a first complication arises due to the fact that the 1s state is a two-fold degenerate state (see Sect. 10.2.2), with two possibilities for the magnetic spin quantum number m _s = −1/2, +1/2. The question is whether both electrons will assume the same (parallel) spin direction (−1/2 and −1/2, or +1/2 and +1/2), or whether they assume different (anti-parallel) directions (−1/2 and +1/2). Analysis of the atomic spectrum of helium shows that only the second scenario agrees with the observed spectrum, therefore, the two electrons occupying the 1s orbital assume anti-parallel spins (Fig. 10.11).

Fig. 10.11

Population of atomic orbitals with electrons for the first ten elements in the periodic system

For the alkali metal lithium, the atomic spectrum indicates a one-electron system, despite the total number of three electrons that need to be considered. This can only be achieved if two electrons occupy the 1s orbital, as in the case of the preceding element (helium), and the third electron occupies the next higher orbital in the scheme (2s). Since the energy of the 2s orbital is higher than that of the 1s orbital, the electrons in the 2s orbital are in a less stable state, and therefore easier to remove from the atom. The ionisation energy of lithium, which can be determined from the atomic spectrum (see Sect. 8.2.1), would thus be expected to be less than the ionisation energy of hydrogen or helium, and this is indeed the case (Fig. 10.12).

Fig. 10.12

The first ionisation energies of elements as a function of their order number (Z) in the periodic system

Another challenge is then observed with carbon. The 2p orbital has already been populated by boron with one electron. The question arises whether the next electron goes into the same p orbital or into another one. And what spin does it assume? Figure 10.11 shows that a new p orbital is occupied, and the spin of the added electron is the same as the one in the first p orbital.

These rules for populating atomic orbitals are known as the Aufbau principle, Pauli exclusion principle and Hund's rules:

The Pauli exclusion principle states that in atomic and molecule systems, two electrons cannot possess the exact same four quantum numbers.

The Aufbau principle is a consequence of the Pauli principle which requires electrons to occupy higher energy levels once lower levels are filled.

According to Hund's rules, if there are multiple orbitals at similar energy levels, electrons populate individual orbitals before pairing up. Unpaired electrons that populate orbitals of the same energy level assume the same spin direction.

The Pauli exclusion principle, formulated by the Austrian physicist Wolfgang Pauli in 1925, is a general quantum mechanical principle that applies to all particles with half-integer spin (so-called fermions). Like the laws of thermodynamics, it is a fundamental principle of observation that cannot be proven.

Hund's rule is also known as the rule of maximum multiplicity. Since electrons are charged particles and pairing them up is energetically costly due to the repelling force between particles of like charges, this is avoided as long as possible. In general, the achievement of half-filled orbitals is preferred, even if an orbital of slightly lower energy is only partially filled as a consequence (see e.g. transition metals).

Above rules enable the prediction of electron configurations of individual atoms (and molecules). When applying these rules to the elements, arranged in increasing order of their nuclear charge (order number Z), the periodicity becomes apparent. These quantum mechanical rules therefore explain the periodic system of the elements which was originally assembled based on chemical and physical properties of the individual elements (and credited to Dmitri Mendeleev in 1869). Table 10.6 summarises the relationships between the quantum numbers, electron configurations and shells.

Table 10.6

The electron configuration and relationships of quantum numbers explain the periodicity in the periodic table of the chemical elements

An obvious illustration of the periodicity caused by the quantum mechanical electron configuration is given by the first ionisation energies, which describe the energy required to remove one (the outermost) electron from the atom (see Fig. 10.12). Their comparison shows that moving from a noble gas to the following alkali metal is accompanied by a drastic lowering of the binding energy of the outermost electron; the binding energy then rises again up to a maximum at the next noble gas. This implies phenomenologically that a new shell of electrons is being filled with each alkali metal.