A Book of Abstract Algebra, Second Edition (1982)

Chapter 11. CYCLIC GROUPS

If G is a group and a ∈ G, it may happen that every element of G is a power of a. In other words, G may consist of all the powers of a, and nothing else:

G = {aⁿ : n ∈ }

In that case, G is called a cyclic group, and a is called its generator. We write

G = ⟨a⟩

and say that G is the cyclic group generated by a.

If G = ⟨a⟩ is the cyclic group generated by a, and a has order n, we say that G is a cyclic group of order n. We will see in a moment that, in that case, G has exactly n elements. If the generator of G has order infinity, we say that G is a cyclic group of order infinity. In that case, we will see that G has infinitely many elements.

The simplest example of a cyclic group is , which consists of all the multiples of 1. (Remember that in additive notation we speak of “multiples” instead of “powers.”) is a cyclic group of order infinity; its generator is 1. Another example of a cyclic group is ₆, which consists of all the multiples of 1, added modulo 6. ₆ is a cyclic group of order 6; 1 is a generator of ₆, but ₆ has another generator too. What is it?

Suppose ⟨a⟩ is a cyclic group whose generator a has order n. Since ⟨a⟩ is the set of all the powers of a, it follows from Theorem 3 of Chapter 10 that

⟨a⟩ = {e,a,a²,...,a^{n −1}}

If we compare this group with _n, we notice a remarkable resemblance! For one thing, they are obviously in one-to-one correspondence:

In other words, the function

f(i) = aⁱ

is a one-to-one correspondence from _n to ⟨a⟩. But this function has an additional property, namely,

f(i + j) = a^{i + j} = aⁱa^j = f(i)f(j)

Thus, f is an isomorphism from _n to ⟨a⟩. In conclusion,

_n ≅ ⟨a⟩

Let us review the situation in the case where a has order infinity. In this case, by Theorem 4 of Chapter 10,

⟨a⟩ = {. . .,a⁻²,a⁻¹, e,a,a²,...}

There is obviously a one-to-one correspondence between this group and :

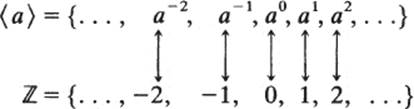
In other words, the function

f(i) = aⁱ

is a one-to-one correspondence from to ⟨a⟩. As before, f is an isomorphism, and therefore

≅ ⟨a⟩

What we have just proved is a very important fact about cyclic groups; let us state it as a theorem.

Theorem 1: Isomorphism of cyclic groups

(i)For every positive integer n, every cyclic group of order n is isomorphic to _n. Thus, any two cyclic groups of order n are isomorphic to each other.

(ii)Every cyclic group of order infinity is isomorphic to , and therefore any two cyclic groups of order infinity are isomorphic to each other.

If G is any group and a ∈ G, it is easy to see that

1. The product of any two powers of a is a power of a; for a^maⁿ = a^{m + n}.

2. Furthermore, the inverse of any power of a is a power of a, because (aⁿ)⁻¹ = a⁻ⁿ.

3. It therefore follows that the set of all the powers of a is a subgroup of G.

This subgroup is called the cyclic subgroup of G generated by a. It is obviously a cyclic group, and therefore we denote it by ⟨a⟩. If the element a has order n, then, as we have seen, ⟨a⟩ contains the n elements {e, a, a²,. . ., a^{n −1}}. If a has order infinity, then ⟨a⟩ = {. . ., a⁻², a⁻¹, e, a, a²,...} and has infinitely many elements.

For example, in , ⟨2⟩ is the cyclic subgroup of which consists of all the multiples of 2. In ₁₅, ⟨3⟩ is the cyclic subgroup {0,3,6,9,12} which contains all the multiples of 3. In S₃, ⟨β⟩ = {ε, β, δ}, and contains all the powers of β.

Can a cyclic group, such as , have a subgroup which is not cyclic? This question is of great importance in our understanding of cyclic groups. Its answer is not obvious, and certainly not self-evident:

Theorem 2 Every subgroup of a cyclic group is cyclic.

Let G = ⟨a⟩ be a cyclic group, and let H be any subgroup of G. We wish to prove that H is cyclic.

Now, G has a generator a; and when we say that H is cyclic, what we mean is that H too has a generator (call it b), and H consists of all the powers of b. The gist of this proof, therefore, is to find a generator of H, and then check that every element of H is a power of this generator.

Here is the idea: G is the cyclic group generated by a, and H is a subgroup of G. Every element of H is therefore in G, which means that every element of H is some power of a. The generator of H which we are searching for is therefore one of the powers of a—one of the powers of a which happens to be in H; but which one? Obviously the lowest one! More accurately, the lowest positive power of a in H.

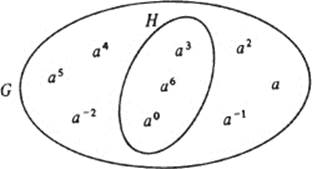
And now, carefully, here is the proof:

PROOF: Let m be the smallest positive integer such that a^m ∈ H. We will show that every element of H is a power of a^m, hence a^m is a generator of H.

Let a^t be any element of H. Divide t by m using the division algorithm:

t = mq + r 0 ≤ r < m

Then a^t = a^{mq + r} = a^mq a^r

Solving for a^r, a^r = (a^mq)⁻¹ a^t = (a^m)^−q a^t

But a^m ∈ H and a^t ∈ H; thus (a^m)^−q ∈ H.

It follows that a^r ∈ H. But r < m and m is the smallest positive iriteger such that a^m ∈ H. So r = 0, and therefore t = mq.

We conclude that every element a^t ∈ H is of the form a^t = (a^m)^q, that is, a power of a^m. Thus, H is the cyclic group generated by a^m. ■

This chapter ends with a final comment regarding the different uses of the word “order” in algebra.

Let G be a group; as we have seen, the order of an element a in G is the least positive integer n such that

(The order of a is infinity if there is no such n.)

Earlier, we defined the order of the group G to be the number of elements in G. Remember that the order of G is denoted by |G|.

These are two separate and distinct definitions, not to be confused with one another. Nevertheless, there is a connection between them: Let a be an element of order n in a group. By Chapter 10, Theorem 3, there are exactly ndifferent powers of a, hence ⟨a⟩ has n elements. Thus,

If ord(a) = n then |⟨a⟩| = n

That is, the order of a cyclic group is the same as the order of its generator.

EXERCISES

A. Examples of Cyclic Groups

1 List the elements of ⟨6⟩ in ₁₆.

2 List the elements of ⟨f⟩ in S₆, where

3 Describe the cyclic subgroup in *. Describe the cyclic group in .

4 If f(x) = x + 1, describe the cyclic subgroup ⟨f⟩ of S_R.

5 If f(x) = x + 1, describe the cyclic subgroup ⟨f⟩ of ().

6 Show that −1, as well as 1, is a generator of . Are there any other generators of ? Explain! What are the generators of an arbitrary infinite cyclic group ⟨a⟩?

7 Is * cyclic? Try to prove your answer. HINT: Suppose k is a generator of *:

If k < 1, then k > k² > k³> ⋯

If k > 1, then k < k² < k³ < ⋯

B. Elementary Properties of Cyclic Groups

Prove each of the following:

# 1 If G is a group of order n, G is cyclic iff G has an element of order n.

2 Every cyclic group is abelian.

3 If G = ⟨a⟩ and b ∈ G, the order of b is a factor of the order of a.

4 In any cyclic group of order n, there are elements of order k for every integer k which divides n.

5 Let G be an abelian group of order mn, where m and n are relatively prime. If G has an element of order m and an element of order n, G is cyclic. (See Chapter 10, Exercise E4.)

6 Let ⟨a⟩ be a cyclic group of order n. If n and m are relatively prime, then the function f(x) = x^m is an automorphism of ⟨a⟩. (HINT: Use Exercise B3 and Chapter 10, Theorem 5.)

C. Generators of Cyclic Groups

For any positive integer n, let ϕ(n) denote the number of positive integers less than n and relatively prime to n. For example, 1, 2, 4, 5, 7, and 8 are relatively prime to 9, so ϕ(9) = 6. Let a have order n, and prove the following:

1 a^r is a generator of ⟨a⟩ iff r and n are relatively prime. (HINT: See Chapter 10, Exercise G2.)

2 ⟨a⟩ has ϕ(n) different generators. (Use part 1 in your proof.)

3 For any factor m of n, let C_m = {x ∈ ⟨a⟩ : x^m = e). C_m is a subgroup of ⟨a⟨.

# 4 C_m has exactly m elements. (HINT: Use Exercise B4.)

5 An element x in ⟨a⟩ has order m iff x is a generator of C_m.

6 There are ϕ(m) elements of order m in ⟨a⟩. (Use parts 1 and 5.)

# 7 Let n = mk. a^r has order m iff r = kl where l and m are relatively prime. (HINT: See Chapter 10, Exercise G1, 2.)

8 If c is any generator of ⟨a⟩, then {c^r : r is relatively prime to n} is the set of all the generators of ⟨a⟩.

D. Elementary Properties of Cyclic Subgroups of Groups

Let G be a group and let a, b ∈ G. Prove the following:

1 If a is a power of b, say a = b^k, then ⟨a⟩ ⊆ ⟨b⟩.

2 Suppose a is a power of b, say a = b^k. Then b is equal to a power of a iff ⟨a⟩ = ⟨b⟩.

3 Suppose a ∈ ⟨b⟩. Then ⟨a⟩ = ⟨b⟩ iff a and b have the same order.

4 Let ord(a) = n, and b = a^k. Then ⟨a⟩ = ⟨b⟩ iff n and k are relatively prime.

5 Let ord(a) = n, and suppose a has a kth root, say a = b^k. Then ⟨a⟩ = ⟨b⟩ iff k and n are relatively prime.

6 Any cyclic group of order mn has a unique subgroup of order n.

E. Direct Products of Cyclic Groups

Let G and H be groups, with a ∈ G and b ∈ H. Prove parts 1-4:

1 If (a, b) is a generator of G × H, then a is a generator of G and b is a generator of H.

2 If G × H is a cyclic group, then G and H are both cyclic.

3 The converse of part 2 is false. (Give an example to demonstrate this.)

4 Let ord(a) = m and ord(b) = n. The order of (a, b) in G × H is the least common multiple of m and n. (HINT: Use Chapter 10, Theorem 5. Nothing else is needed!)

5 Conclude from part 4 that if m and n are relatively prime, then (a, b) has order mn.

6 Suppose (c, d) ∈ G × H, where c has order m and d has order n. Prove: If m and n are not relatively prime (hence have a common factor q > 1), then the order of (c, d) is less than mn.

7 Conclude from parts 5 and 6 that ⟨a⟩ × ⟨b⟩ is cyclic iff ord(a) and ord(b) are relatively prime.

8 Let G be an abelian group of order mn, where m and n are relatively prime. Prove: If G has an element a of order m and an element b of order n, then G ≅ ⟨a⟩ × ⟨b⟩. (HINT: See Chapter 10, Exercise E1, 2.)

9 Let ⟨a⟩ be a cyclic group of order mn, where m and n are relatively prime, and prove that ⟨a⟩ ≅ ⟨a^m⟩ × ⟨aⁿ⟩.

† F. kth Roots of Elements in a Cyclic Group

Let ⟨a⟩ be a cyclic group of order n. For any integer k, we may ask: which elements in ⟨a⟩ have a kth root? The exercises which follow will answer this question.

1 Let a have order 10. For what integers k (0 ≤ k ≤ 12), does a have a kth root? For what integers k (0 ≤ k ≤ 12), does a⁶ have fcth root?

Let k and n be any integers, and let gcd(k, n) denote the greatest common divisor of k and n. A linear combination of k and n is any expression ck + dn where c and d are integers. It is a simple fact of number theory (the proof is given on page 219), that an integer m is equal to a linear combination of k and n iff m is a multiple of gcd(k, n). Use this fact to prove the following, where a is an element of order n in a group G.

2 If m is a multiple of gcd(k, n), then a^m has a kth root in ⟨a⟩. [HINT: Compute a^m, and show that a^m = (a^c)^k for some a^c ∈ ⟨a⟩.]

# 3 If a^m has a kth root in ⟨a⟩, then m is a multiple of gcd(k, n). Thus, a^m has a kth root in ⟨a⟩ iff gcd(k, n) is a factor of m.

4 a has a kth root in ⟨a⟩ iff k and n are relatively prime.

5 Let p be a prime number.

(a) If n is not a multiple of p, then every element in ⟨a⟩ has a pth root.

(b) If n is a multiple of p, and a^m has a pth root, then m is a multiple of p.

(Thus, the only elements in ⟨a⟩ which have pth roots are e, a^p, a^2p, etc.)

6 The set of all the elements in ⟨a⟩ having a kth root is a subgroup of ⟨a⟩. Explain why this subgroup is cyclic, say ⟨a^m⟩. What is the value of m? (Use part 3.)