A Book of Abstract Algebra, Second Edition (1982)
Chapter 13. COUNTING COSETS
Just as there are great works in art and music, there are also great creations of mathematics. “Greatness,” in mathematics as in art, is hard to define, but the basic ingredients are clear: a great theorem should contribute substantial new information, and it should be unexpected!. That is, it should reveal something which common sense would not naturally lead us to expect. The most celebrated theorems of plane geometry, as may be recalled, come as a complete surprise; as the proof unfolds in simple, sure steps and we reach the conclusion—a conclusion we may have been skeptical about, but which is now established beyond a doubt—we feel a certain sense of awe not unlike our reaction to the ironic or tragic twist of a great story.
In this chapter we will consider a result of modern algebra which, by all standards, is a great theorem. It is something we would not likely have foreseen, and which brings new order and simplicity to the relationship between a group and its subgroups.
We begin by adding to our algebraic tool kit a new notion—a conceptual tool of great versatility which will serve us well in all the remaining chapters of this book. It is the concept of a coset.
Let G be a group, and H a subgroup of G. For any element a in G, the symbol
aH
denotes the set of all products ah, as a remains fixed and h ranges over H. aH is called a left coset of H in G.
In similar fashion
Ha
denotes the set of all products ha, as a remains fixed and h ranges over H. Ha is called a right coset of H in G.
In practice, it will make no difference whether we use left cosets or right cosets, just as long as we remain consistent. Thus, from here on, whenever we use cosets we will use right cosets. To simplify our sentences, we will say coset when we mean “right coset.”
When we deal with cosets in a group G, we must keep in mind that every coset in G is a subset of G. Thus, when we need to prove that two cosets Ha and Hb are equal, we must show that they are equal sets. What this means, of course, is that every element x ∈ Ha is in Hb, and conversely, every element y ∈ Hb is in Ha. For example, let us prove the following elementary fact:
If a ∈ Hb, then Ha = Hb(1)
We are given that a ∈ Hb, which means that a = h1b for some h1 ∈ H. We need to prove that Ha = Hb.
Let x ∈ Ha; this means that x = h2a for some h2 ∈ H. But a = h1b, so x = h2a = (h2h1)b, and the latter is clearly in Hb. This proves that every x ∈ Ha is in Hb; analogously, we may show that every y∈ Hb is in Ha, and therefore Ha = Hb.
The first major fact about cosets now follows. Let G be a group and let H be a fixed subgroup of G:
Theorem 1 The family of all the cosets Ha, as a ranges over G, is a partition of G.
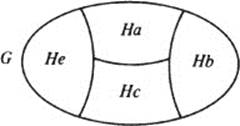
PROOF: First, we must show that any two cosets, say Ha and Hb, are either disjoint or equal. If they are disjoint, we are done. If not, let x ∈ Ha ∩ Hb. Because x ∈ Ha, x = hxa for some h1 ∈ H. Because x ∈ Hb, x = h2b for some h2 ∈ H. Thus, h1a = h2b, and solving for a, we have
Thus,
a ∈ Hb
It follows from Property (1) above that Ha = Hb.
Next, we must show that every element c ∈ G is in one of the cosets of H. But this is obvious, because c = ec and e ∈ H; therefore,
c = ec ∈ Hc
Thus, the family of all the cosets of H is a partition of G. ■
Before going on, it is worth making a small comment: A given coset, say Hb, may be written in more than one way. By Property (1) if a is any element in Hb, then Hb is the same as Ha. Thus, for example, if a coset of Hcontains n different elements a1, a2, …, an, it may be written in n different ways, namely, Ha1, Ha2, …, Han.
The next important fact about cosets concerns finite groups. Let G be a finite group, and H a subgroup of G. We will show that all the cosets of H have the same number of elements! This fact is a consequence of the next theorem.
Theorem 2 If Ha is any coset of H, there is a one-to-one correspondence from H to Ha.
PROOF: The most obvious function from H to Ha is the one which, for each h ∈ H, matches h with ha. Thus, let f: H → Ha be defined by
f(h) = ha
Remember that a remains fixed whereas h varies, and check that f is injective and surjective.
f is injective: Indeed, if f(h1) = f(h2), then h1a = h2a, and therefore h1 = h2.
f is surjective, because every element of Ha is of the form ha for some h ∈ H, and ha = f(h).
Thus, f is a one-to-one correspondence from H to Ha, as claimed. ■
By Theorem 2, any coset Ha has the same number of elements as H, and therefore all the cosets have the same number of elements!
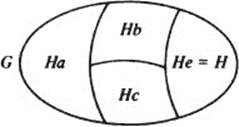
Let us take a careful look at what we have proved in Theorems 1 and 2. Let G be a finite group and H any subgroup of G. G has been partitioned into cosets of H, and all the cosets of H have the same number of elements (which is the same as the number of elements in H). Thus, the number of elements in G is equal to the number of elements in H, multiplied by the number of distinct cosets of H. This statement is known as Lagrange’s theorem. (Remember that the number of elements in a group is called the group’s order.)
Theorem 3: Lagrange’s theorem Let G be a finite group, and H any subgroup of G. The order of G is a multiple of the order of H.
In other words, the order of any subgroup of a group G is a divisor of the order of G.
For example, if G has 15 elements, its proper subgroups may have either 3 or 5 elements. If G has 7 elements, it has no proper subgroups, for 7 has no factors other than 1 and 7. This last example may be generalized:
Let G be a group with a prime number p of elements. If a ∈ G where a ≠ e, then the order of a is some integer m ≠ 1. But then the cyclic group ⟨a⟩ has m elements. By Lagrange’s theorem, m must be a factor of p. But p is a prime number, and therefore m = p. It follows that ⟨a⟩ has p elements, and is therefore all of G! Conclusion:
Theorem 4 If G is a group with a prime number p of elements, then G is a cyclic group. Furthermore, any element a ≠ e in G is a generator of G.
Theorem 4, which is merely a consequence of Lagrange’s theorem, is quite remarkable in itself. What it says is that there is (up to isomorphism) only one group of any given prime order p. For example, the only group (up to isomorphism) of order 7 is 
7, the only group of order 11 is 11, and so on! So we now have complete information about all the groups whose order is a prime number.
By the way, if a is any element of a group G, the order of a is the same as the order of the cyclic subgroup ⟨a⟩, and by Lagrange’s theorem this number is a divisor of the order of G. Thus,
Theorem 5 The order of any element of a finite group divides the order of the group.
Finally, if G is a group and H is a subgroup of G, the index of H in G is the number of cosets of H in G. We denote it by (G:H). Since the number of elements in G is equal to the number of elements in H, multiplied by the number of cosets of H in G,
EXERCISES
A. Examples of Cosets in Finite Groups
In each of the following, H is a subgroup of G. In parts 1–5 list the cosets of H. For each coset, list the elements of the coset.
Example G = 4, H = {0, 2}.
(REMARK: If the operation of G is denoted by +, it is customary to write H + x for a coset, rather than Hx.) The cosets of H in this example are
H = H + 0 = H + 2 = {0, 2}andH+ 1 = H + 3 = {1, 3}
1G = S3, H = {ε, β, δ}.
2G = S3, H = {ε, α}.
3G = 15, H = ⟨5⟩.
4G = D4, H ={R0, R4}.(For D4, see page 73.)
5G = S4, H = A4.(For A4, see page 86.)
6Indicate the order and index of each of the subgroups in parts 1 to 5.
B. Examples of Cosets in Infinite Groups
Describe the cosets of the subgroups described in parts 1–5:
# 1The subgroup ⟨3⟩ of .
2The subgroup of 
.
3The subgroup H = {2n: n ∈ } of *.
4The subgroup ⟨
⟩ of R*; the subgroup ⟨⟩ of .
5The subgroup H = {(x, y): x = y} of ( × .
6For any positive integer m, what is the index of ⟨m⟩ in ?
7Find a subgroup of * whose index is equal to 2.
C. Elementary Consequences of Lagrange’s Theorem
Let G be a finite group. Prove the following:
1 If G has order n, then xn = e for every x in G.
2 Let G have order pq, where p and q are primes. Either G is cyclic, or every element x ≠ e in G has order p or q.
3 Let G have order 4. Either G is cyclic, or every element of G is its own inverse. Conclude that every group of order 4 is abelian.
4 If G has an element of order p and an element of order q, where p and q are distinct primes, then the order of G is a multiple of pq.
5 If G has an element of order k and an element of order m, then |G| is a multiple of lcm(k, m), where lcm(k, m) is the least common multiple of k and m.
# 6 Let p be a prime number. In any finite group, the number of elements of order p is a multiple of p − 1.
D. Further Elementary Consequences of Lagrange’s Theorem
Let G be a finite group, and let H and K be subgroups of G. Prove the following:
1 Suppose H ⊆ K (therefore H is a subgroup of K). Then (G: H) = (G: K)(K: H).
2 The order of H ∩ K is a common divisor of the order of H and the order of K.
3 Let H have order m and K have order n, where m and n are relatively prime. Then H ∩ K = {e}.
4 Suppose H and K are not equal, and both have order the same prime number p. Then H ∩ K = {e}.
5 Suppose H has index p and K has index p, where p and g are distinct primes. Then the index of H ∩ K is a multiple of pq.
# 6 If G is an abelian group of order n, and m is an integer such that m and n are relatively prime, then the function f(x) = xm is an automorphism of G.
E. Elementary Properties of Cosets
Let G be a group, and H a subgroup of G. Let a and b denote elements of G. Prove the following:
1 Ha = Hb iff ab−1 ∈ H.
2 Ha = H iff a ∈ H.
3 If aH = Ha and bH = Hb, then (ab)H = H(ab).
# 4 If aH = Ha, then a−1H = Ha−1.
5 If (ab)H = (ac)H, then bH = cH.
6 The number of right cosets of H is equal to the number of left cosets of H.
7 If J is a subgroup of G such that J = H ∩ K, then for any a ∈ G, Ja = Ha ∩ Ka. Conclude that if H and K are of finite index in G, then their intersection H ∩ K is also of finite index in G.
Theorem 5 of this chapter has a useful converse, which is the following:
Cauchy’s theorem If G is a finite group, and p is a prime divisor of |G|, then G has an element of order p.
For example, a group of order 30 must have elements of orders 2, 3, and 5. Cauchy’s theorem has an elementary proof, which may be found on page 340.
In the next few exercise sets, we will survey all possible groups whose order is ≤10. By Theorem 4 of this chapter, if G is a group with a prime number p of elements, then G ≅ p. This takes care of all groups of orders 2, 3 5, and 7. In Exercise G6 of Chapter 15, it will be shown that if G is a group with p2 elements (where p is a prime), then G ≅p2 or G ≅ p × p. This will take care of all groups of orders 4 and 9. The remaining cases are examined in the next three exercise sets.
† F. Survey of All Six-Element Groups
Let G be any group of order 6. By Cauchy’s theorem, G has an element a of order 2 and an element b of order 3. By Chapter 10, Exercise E3, the elements
e, a, b, b2, ab, ab2
are all distinct; and since G has only six elements, these are all the elements in G. Thus, ba is one of the elements e, a, b, b2, ab, or ab2.
1 Prove that ba cannot be equal to either e, a, b, or b2. Thus, ba = ab or ba = ab2.
Either of these two equations completely determines the table of G. (See the discussion at the end of Chapter 5.)
2 If ba = ab, prove that G ≅ 6.
3 If ba = ab2, prove that G ≅ S3.
It follows that 6 and S3 are (up to isomorphism), the only possible groups of order 6.
† G. Survey of All 10-EIement Groups
Let G be any group of order 10.
1 Reason as in Exercise F to show that G = {e, a, b, b2, b3, b4, ab, ab2, ab3, ab4}, where a has order 2 and b has order 5.
2 Prove that ba cannot be equal to e, a, b, b2, b3, or b4.
3 Prove that if ba = ab, then G ≅ 10.
4 If ba = ab2, prove that ba2 = a2b4, and conclude that b = b4. This is impossible because b has order 5; hence ba ≠ ab2. (HINT: The equation ba = ab2 tells us that we may move a factor a from the right to the left of a factor b, but in so doing, we must square b. To prove an equation such as the preceding one, move all factors a to the left of all factors b.)
5 If ba = ab3, prove that ba2 = a2b9 = a2b4, and conclude that b = b4. This is impossible (why?); hence ba ≠ ab3.
6 Prove that if ba = ab4, then G ≅ D5 (where D5 is the group of symmetries of the pentagon).
Thus, the only possible groups of order 10 (up to isomorphism), are 10 and D5.
† H. Survey of All Eight-Element Groups
Let G be any group of order 8. If G has an element of order 8, then G ≅ 8. Let us assume now that G has no element of order 8; hence all the elements ≠ e in G have order 2 or 4.
1 If every x ≠ e in G has order 2, let a, b, c be three such elements. Prove that G = {e, a, b, c, ab, bc, ac, abc}. Conclude that G ≅ 2 × 2 × 2.
In the remainder of this exercise set, assume G has an element a of order 4. Let H = ⟨a⟩ = {e, a, a2, a3}. If b ∈ G is not in H, then the coset Hb = {b, ab, a2b, a3b}. By Lagrange’s theorem, G is the union of He = H and Hb; hence
G = {e, a, a2, a3, b, ab, a2b, a3b}
2 Assume there is in Hb an element of order 2. (Let b be this element.) If ba = a2b, prove that b2a = a4b2, hence a = a4, which is impossible. (Why?) Conclude that either ba = ab or ba = a3b.
3 Let b be as in part 2. Prove that if ba = ab, then G ≅ 4 × 2.
4 Let b be as in part 2. Prove that if ba = a3b, then G ≅ D4.
5 Now assume the hypothesis in part 2 is false. Then b, ab, a2b, and a3b all have order 4. Prove that b2 = a2. (HINT: What is the order of b2? What element in G has the same order?)
6 Prove: If ba = ab, then (a3b)2 = e, contrary to the assumption that ord(a3b) = 4. If ba = a2b, then a = b4a = e, which is impossible. Thus, ba = a3b.
7 The equations a4 = b4 = e, a2 = b2, and ba = a3b completely determine the table of G. Write this table. (G is known as the quarternion group Q.)
Thus, the only groups of order 8 (up to isomorphism) are 8, 2 × 2 × 2, 4 × 2, D4, and Q.
† I. Conjugate Elements
If a ∈ G, a conjugate of a is any element of the form xax−1, where x ∈ G. (Roughly speaking, a conjugate of a is any product consisting of a sandwiched between any element and its inverse.) Prove each of the following:
1 The relation “a is equal to a conjugate of b” is an equivalence relation in G. (Write a ∼ b for “a is equal to a conjugate of b.”)
This relation ∼ partitions any group G into classes called conjugacy classes. (The conjugacy class of a is [a] = {xax−1: x ∈ G}.)
For any element a ∈ G, the centralizer of a, denoted by Ca, is the set of all the elements in G which commute with a. That is,
Ca = {x ∈ G: xa = ax} = {x ∈ G: xax−1 = a}
Prove the following:
2 For any a ∈ G, Ca is a subgroup of G.
3 x−1ax = y−1ay iff xy−1 commutes with a iff xy−1 ∈ Ca.
4 x−1ax = y−1ay iff Cax = Cay. (HINT: Use Exercise El.)
5 There is a one-to-one correspondence between the set of all the conjugates of a and the set of all the cosets of Ca. (HINT: Use part 4.)
6 The number of distinct conjugates of a is equal to (G: Ca), the index of Ca in G. Thus, the size of every conjugacy class is a factor of |G.
† J. Group Acting on a Set
Let A be a set, and let G be any subgroup of SA. G is a group of permutations of A; we say it is a group acting on the set A. Assume here that G is a finite group. If u ∈ A, the orbit of u (with respect to G) is the set
O(u) = {g(u): g ∈ G}
1 Define a relation ∼ on A by u ∼ υ iff g(w) = υ for some g ∈ G. Prove that ∼ is an equivalence relation on A, and that the orbits are its equivalence classes.
If u ∈ A, the stabilizer of u is the set Gu = {g ∈ G: g(u) = u}, that is, the set of all the permutations in G which leave u fixed.
2 Prove that Gu is a subgroup of G.
# 3 Let α = (1 2)(3 4)(5 6) and β = (2 3) in S6. Let G be the following subgroup of S6: G = {ε, α, β, αβ, βα, αβα, βαβ, (αβ)2}.Find O(1), O(2), O(5), G1, G2, G4, G5.
4 Let f, g ∈ G. Prove that f and g are in the same left coset of Gu iff f(u) = g(u). (HINT: Use Exercise El modified for left cosets.)
5 Use part 4 to show that the number of elements in O(u) is equal to the index of Gu in G. [HINT: If f(u) = υ, match the coset of f with υ.]
6 Conclude from part 5 that the size of every orbit (with respect to G) is a factor of the order of G. In particular, if f ∈ SA, the length of each cycle of f is a factor of the order of f in SA.
K. Coding Theory: Coset Decoding
In order to undertake this exercise set, the reader should be familiar with the introductory paragraphs (preceding the exercises) of Exercises F and G of Chapter 3 and Exercise H of Chapter 5.
Recall that 
is the group of all binary words of length n. A group code C is a subgroup of . To decode a received word x means to find the codeword a closest to x, that is, the codeword a such that the distance d(a, x) is a minimum.
But d(a, x) = w(a + x), the weight (number of Is) of a + x. Thus, to decode a received word x is to find the codeword a such that the weight w(a + x) is a minimum. Now, the coset C + x consists of all the sums c + x as c ranges over all the codewords; so by the previous sentence, if a + x is the word of minimum weight in the coset C + x, then a is the word to which x must be decoded.
Now a = (a + x) + x; so a is found by adding x to the word of minimum weight in the coset C + x. To recapitulate: In order to decode a received word x you examine the coset C + x, find the word e of minimum weight in the coset (it is called the coset leader), and add e to x. Then e + x is the codeword closest to x, and hence the word to which x must be decoded.
1 Let C1 be the code described in Exercise G of Chapter 3.
(a)List the elements in each of the cosets of C1.
(b)Find a coset leader in each coset. (There may be more than one word of minimum weight in a coset; choose one of them as coset leader.)
(c)Use the procedure described above to decode the following words x: 11100, 01101, 11011, 00011.
2 Let C3 be the Hamming code described in Exercise H2 of Chapter 5. List the elements in each of the cosets of C3 and find a leader in each coset. Then use coset decoding to decode the following words x: 1100001, 0111011, 1001011.
3 Let C be a code and let H be the parity-check matrix of C. Prove that x and y are in the same coset of C if and only if Hx = Hy. (HINT: Use Exercise H8, Chapter 5.)
If x is any word, Hx is called the syndrome of x. It follows from part 3 that all the words in the same coset have the same syndrome, and words in different cosets have different syndromes. The syndrome of a word x is denoted by syn(x).
4 Let a code C have q cosets, and let the coset leaders be e1, e2, …, eq. Explain why the following is true: To decode a received word x, compare syn(x) with syn(e1, …, syn(eq) and find the coset leader ei such that syn(x) = syn(ei). Then x is to be decoded to x + ei.
5 Find the syndromes of the coset leaders in part 2. Then use the method of part 4 to decode the words x = 1100001 and x = 1001011.