High School Algebra I Unlocked (2016)

Lesson 4.4. Two-Variable Linear Equations

Up until now, we’ve only discussed equations with a single variable; for example, x = 2 or y + 3 = 2y. However, in algebra, you will encounter tons of questions that require you to manipulate and graph two-variable equations.

Graphing and the Coordinate Plane

Graphing is a way of representing a point in two dimensions on what is known as a Cartesian grid or coordinate plane. Here’s the Cartesian grid:

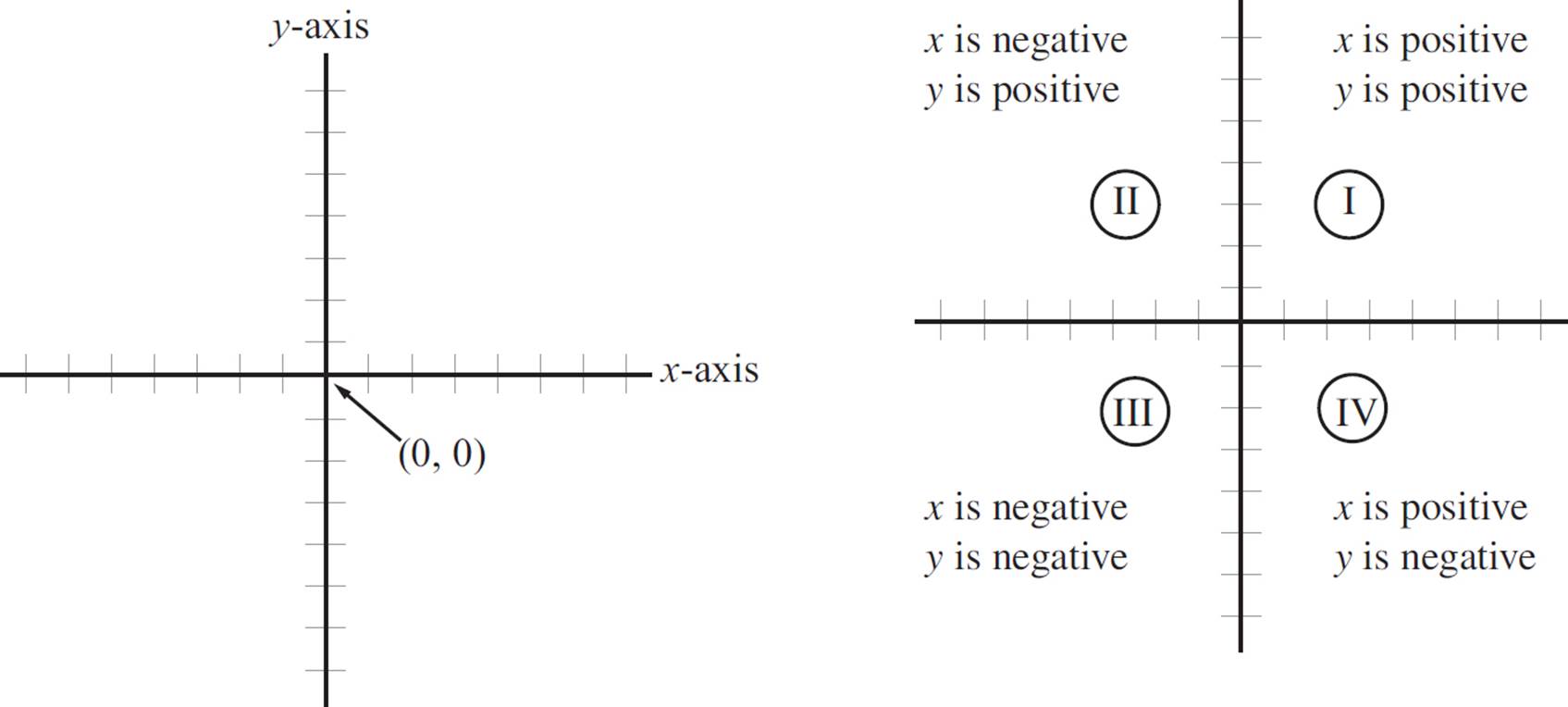
Here is how you may see equivalent expressions on the ACT.

−x³ + 24x + 75 + 34x³ − 36x is equivalent to:

F. 99x

G. −35x³

H. 24x + 75

J. 33x³ − 12x + 75

K. 35x³ + 12x + 75

Graphing is a way of assigning points to this grid. Every point has two numbers assigned to it: an x-coordinate and a y-coordinate. Let’s take point A (3, 1) in the following graph. The first number is considered the x-coordinate, and the second number is the y-coordinate. To plot this point on the graph, we start at (0, 0), also referred to as the origin, and count over three to the right on the x-axis, and then count up one place parallel to the y-axis. To find point B (5, 4), we move five places to the right of the origin on the x-axis, and then up four places parallel to the y-axis.

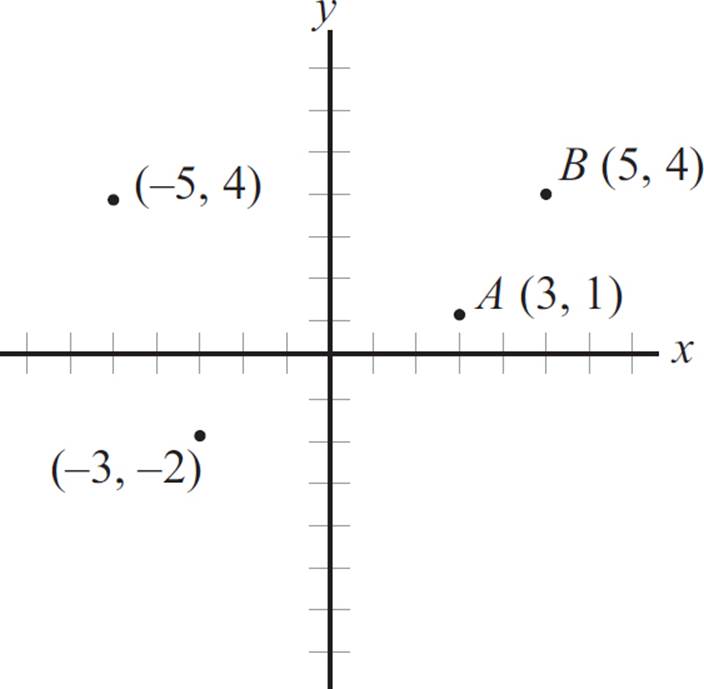
If the x-coordinate is negative, move to the left along the x-axis. If the y-coordinate is negative, then you move downward parallel to the y-axis. Look at the graph above to see how points (−5, 4) and (−3, −2) are plotted.

Slope-Intercept Form

In order to graph linear equations with ease, you need to be familiar with the slope-intercept form of a line:

y = mx + b

When an equation is in slope-intercept form, m represents the slope, or the measure of the steepness of a line, and b represents the y-intercept, or the y-coordinate of the point on the line that crosses the y-axis and has an x-coordinate of 0. To find the x-intercept, set y equal to zero and solve for x.

The slope-intercept form of a line is y = mx + b.

m = Slope   b = y-intercept

The x-intercept is found by setting y = 0 and solving for x.

As shown in the chart below, the slope of a line can be increasing, decreasing, zero, or undefined, depending on the value of m.

Graphs of Single-Variable Linear Equations

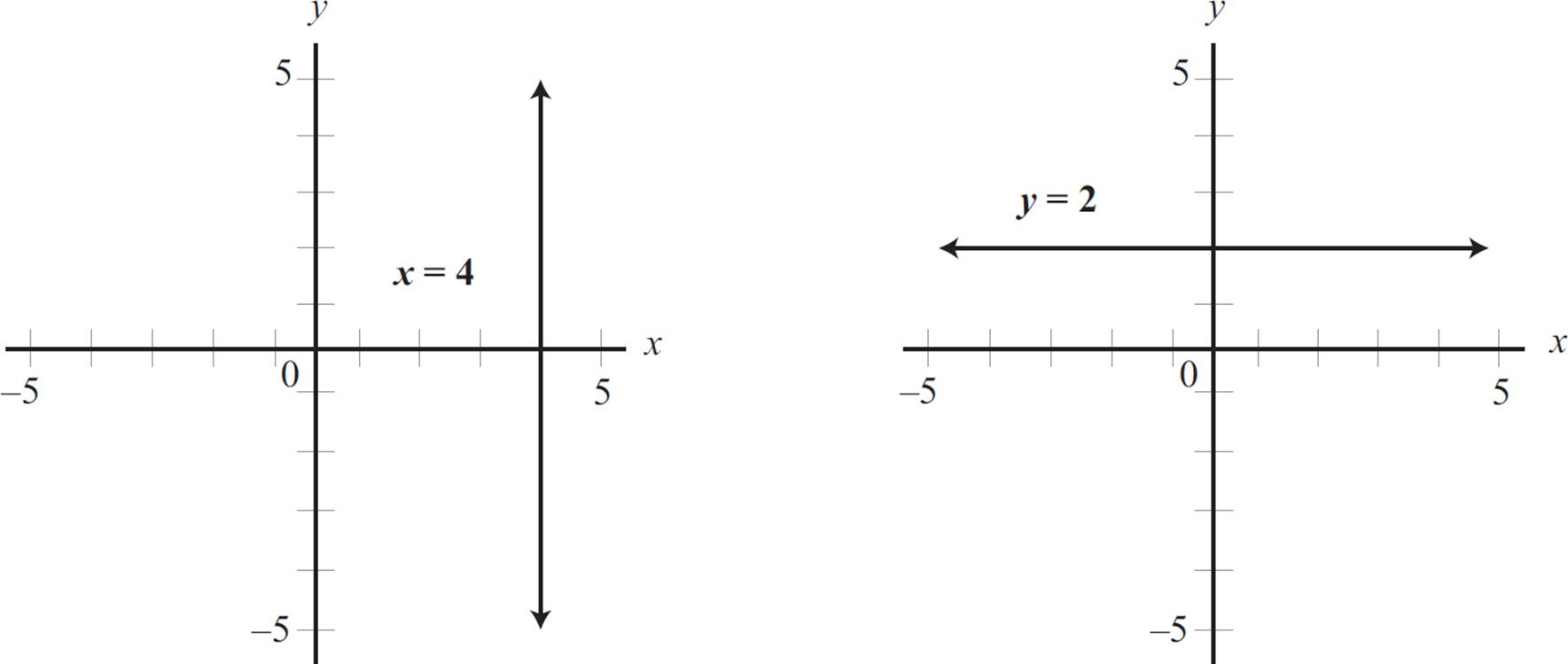
If you’re wondering why we didn’t cover graphs of single-variable linear equations, consider the equation x = 4. This equation indicates that x = 4 for all values of y and, therefore, is a straight vertical line. For all equations that are in the form of x = any number, the slope is undefined.

Conversely, the equation y = 2 indicates that y = 2 for all values of x and, in turn, is a straight horizontal line. For all equations that are in the form of y = any number, the slope is 0. On the next page, you can see the graphs of both x = 4 and y = 2.

Start by grouping similar terms. Here, you have −x³ + 34x³ = 33x³. You can eliminate (F), (G), and (H) because they do not have the term 33x³ in their expressions. Next, you have 24x − 36x = −12x. The only answer choice that has the term −12x is (J).

Alternatively, you could plug in a value for x, find the value of −x³ + 24x + 75 + 34x³ −36x. Since there are exponents, pick a small number, like 2. When you set x = 2, the equation −x³ + 24x + 75 + 34x³ − 36x becomes −2³ + 24(2) + 75 + 34(2)³ − 36(2). This simplifies to −8 + 48 + 75 + 272 − 72 = 315. Now, plug x = 2 into the answer choices, looking for the value of 315. Only (J), 33(2)³ − 12(2) + 75 = 264 − 24 + 75 = 315, provides that value.

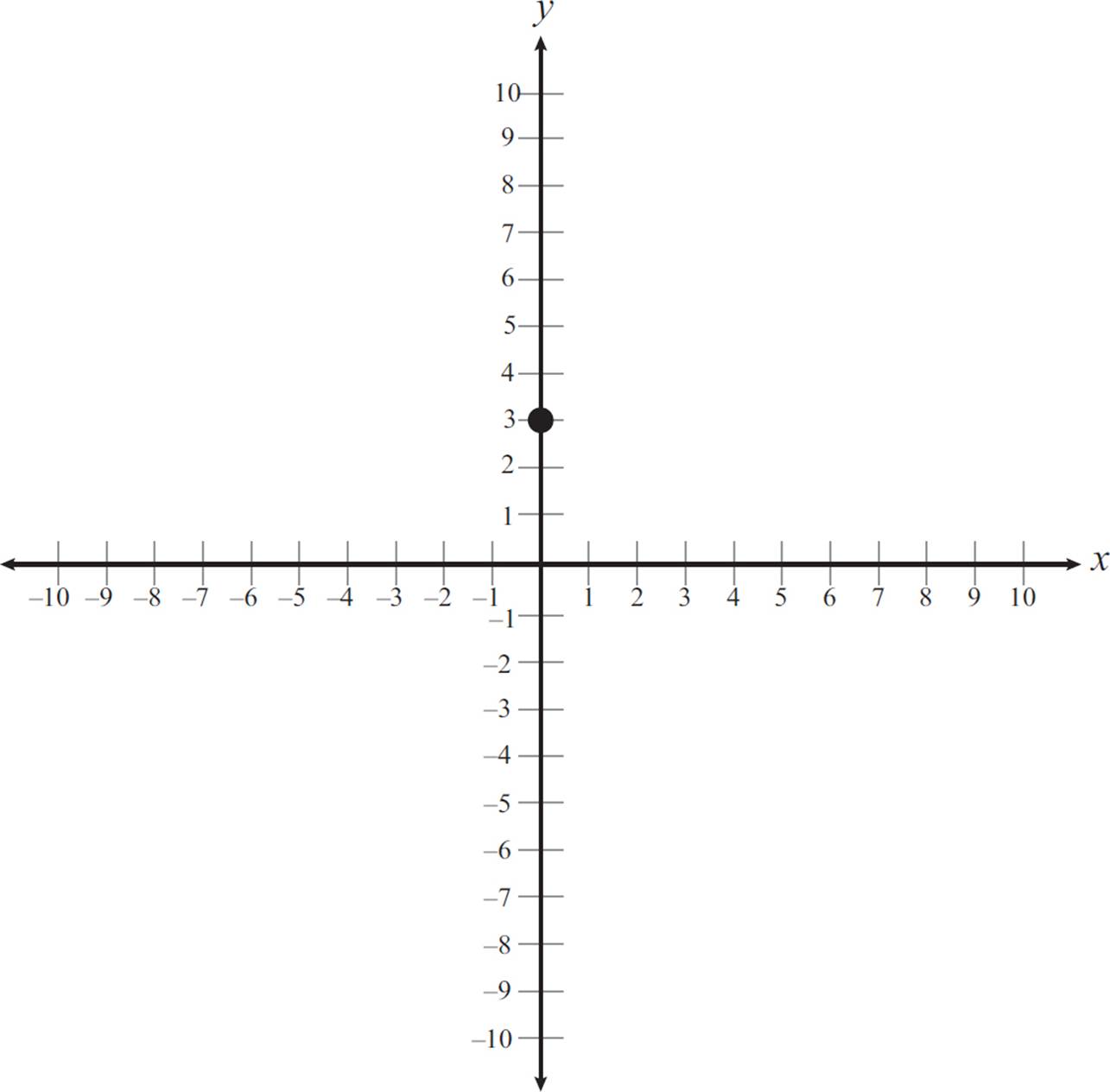
Consider the equation y = 2x + 3. Start out by identifying the y-intercept, which is 3. Since the y-intercept is 3, the graph includes the point (0, 3). This can be plotted on the graph, as shown.

The slope is 2, and since slope is equal to rise/run, the y-coordinate increases by 2 as the x-coordinate increases by 1. Use this to plot additional points. Start with point (0, 3) and increase the x-coordinate by 1 and y-coordinate by 2 to get (1, 5). Do this again to get (2, 7) and (3, 9). Similarly, you can go backwards. Go back to the point (0, 3) and decrease the x-coordinate by 1 and the y-coordinate by 2 to get (−1, 1), and again to get (−2, −1) and (−3, −3). Plot these points as well.

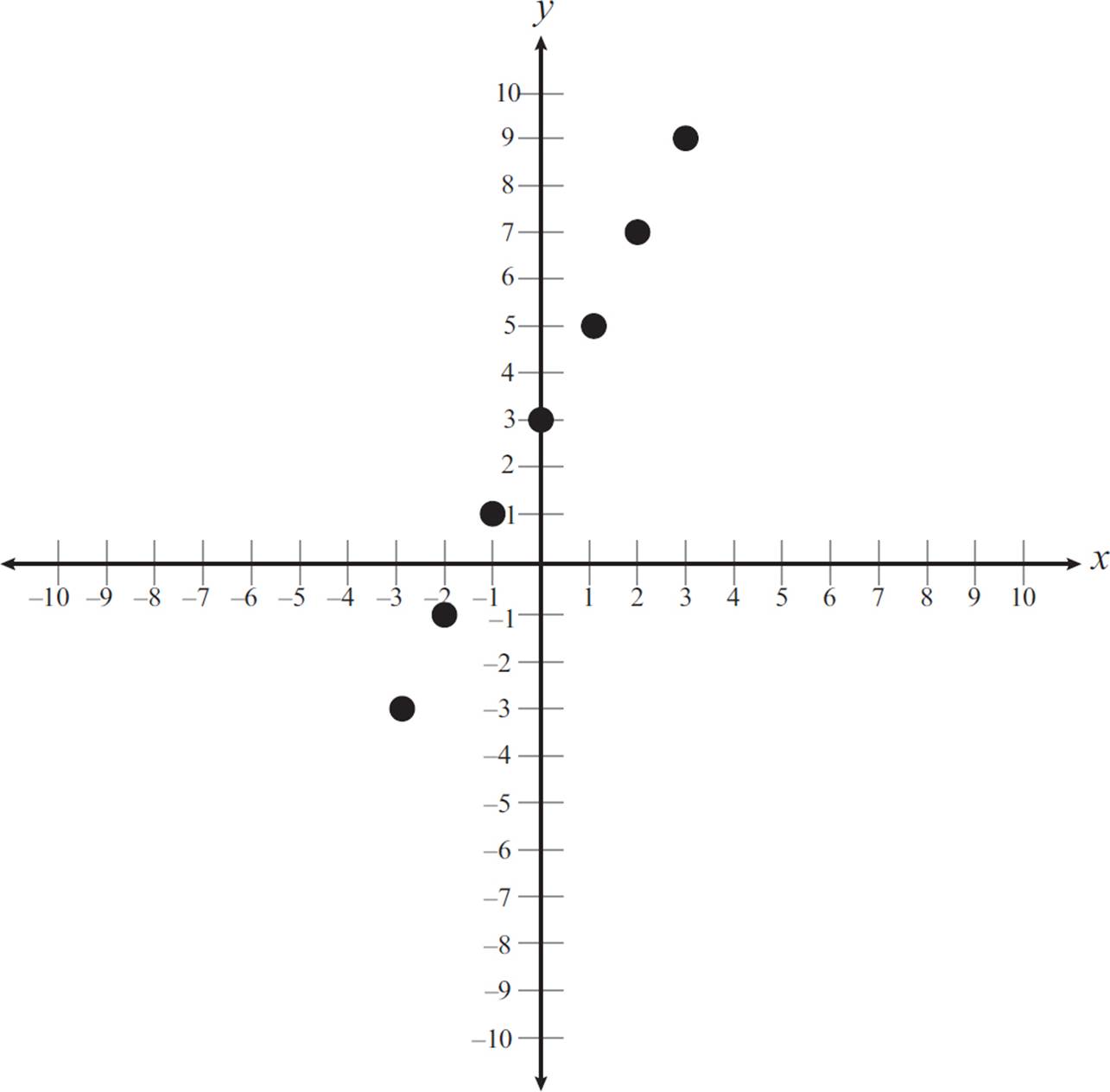
Finally, draw a line that goes through all these points, as shown in the following graph.

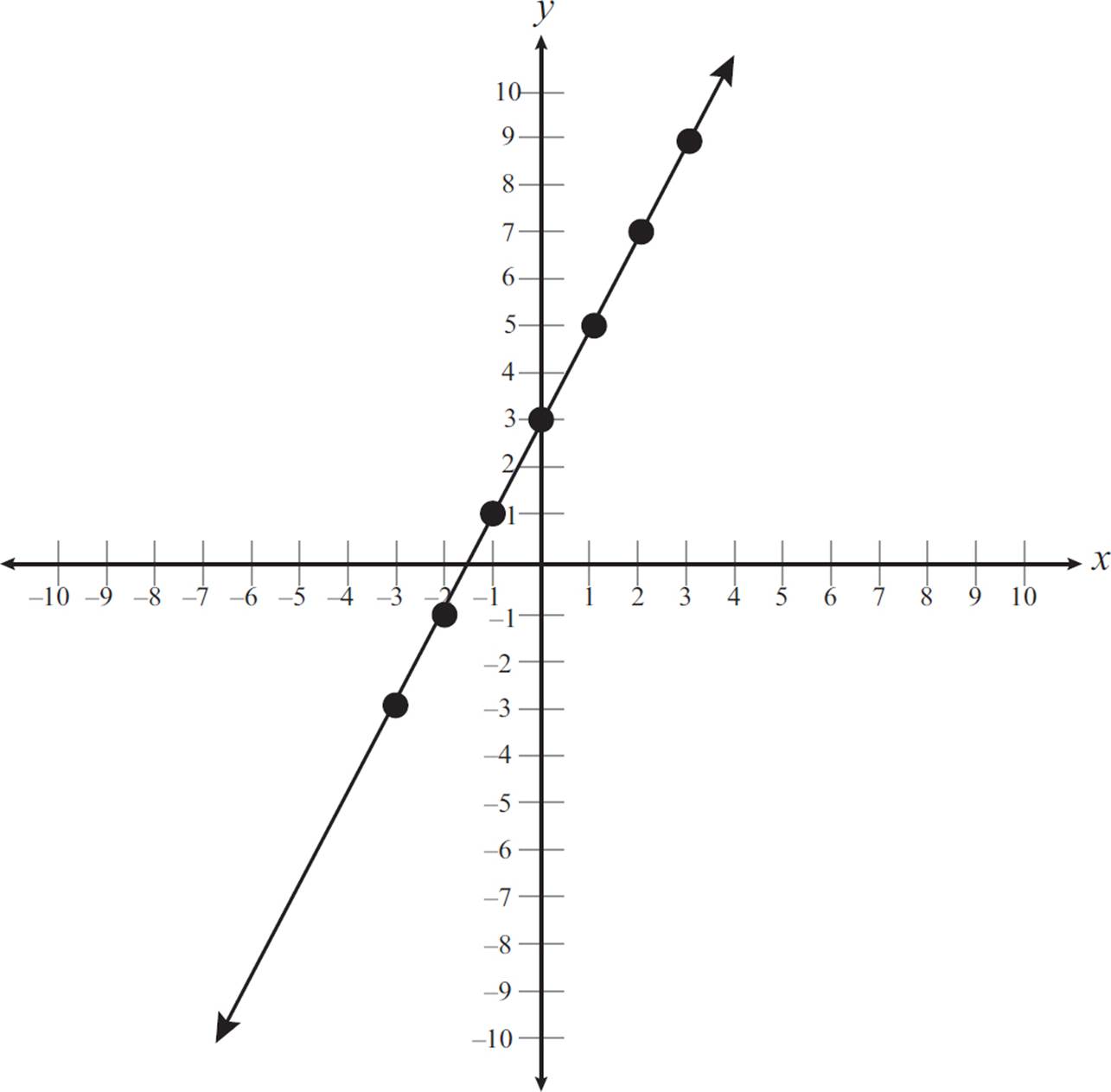
This line is a graphical representation of the two-variable linear equation y = 2x + 3.

Slope can also be found from two points on a coordinate plane using the following formula:

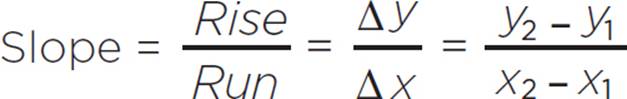
Imagine that you were given the following graph, but not given the equation for the line. How would you find the slope?

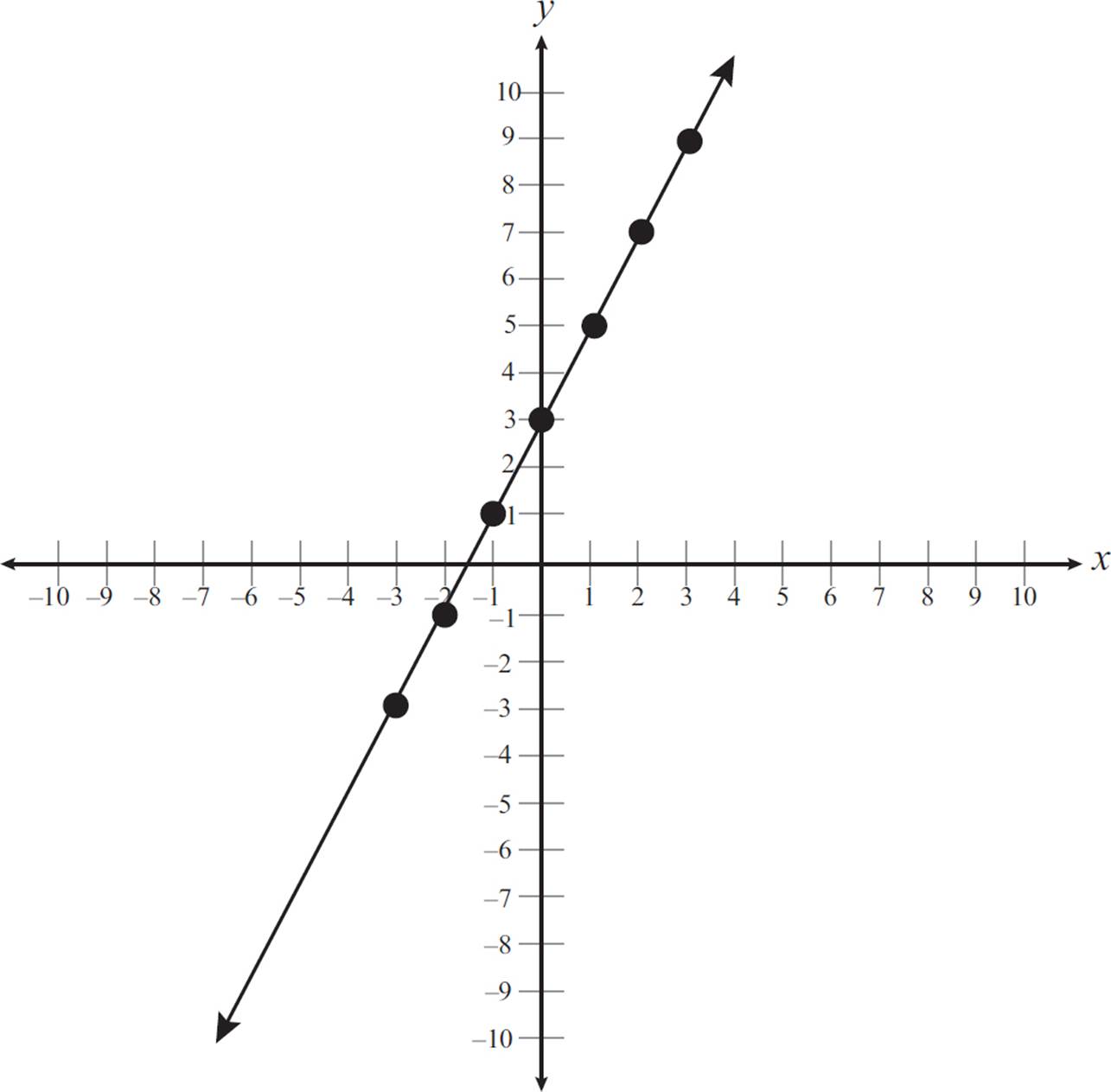
If you know two points on a coordinate plane, the slope of a line can also be found by using the formula 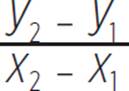. In the previous graph, there are points at (0, 3) and (−2, −1). You can find the slope, m, by substituting those points into the following formula:

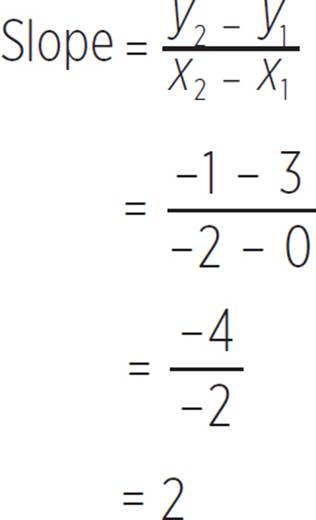
Thus, the line in this graph has a slope of 2. Note that the slope of 2 aligns with the value of m in the equation y = 2x + 3.

Now that we’ve learned about two-variable equations, graphs, and slope, let’s try a few questions that deal with these concepts.

EXAMPLE

Rewrite the equation of the line 4x + 12 = 2y in slope-intercept form, and identify the x- and y-intercepts of the equation.

This question asks you to rewrite the equation in slope-intercept form, or y = mx + b. Start by rewriting the equation with the y-term to the left of the equals sign and the other terms to the right of the equals sign.

4x + 12 = 2y

2y = 4x + 12

Next, divide both sides of the equation by 2.

2y = 4x + 12

y = 2x + 6

That’s it! The equation 4x + 12 = 2y in slope-intercept form is y = 2x + 6. Now you need to identify the x- and y-intercepts of the equation. In order to find the x-intercept, set y = 0 and solve for x:

y = 2x + 6

0 = 2x + 6

2x = −6

x = −3

Excellent! You found that the x-intercept is (−3, 0). Now you need to find the y-intercept, which is the value of b when an equation is written in slope-intercept form, y = mx + b. Since the equation 4x + 12 = 2y has already been converted to slope-intercept form as y = 2x + 6, the y-intercept occurs at (0, 6).

Therefore, the equation 4x + 12 = 2y is written in slope-intercept form as y = 2x + 6, the x-intercept of the equation is (−3, 0), and the y-intercept is (0, 6).

Let’s build on this question.

EXAMPLE

What is the slope of line 4x + 12 = 2y ?

You probably noticed that the equation here is the same one from Example 11. You should have also noticed that the slope is not easily identifiable in the equation 4x + 12 = 2y. So, as before, you will need to start by rewriting the equation in slope-intercept form.

4x + 12 = 2y

2y = 4x + 12

Next, divide both sides of the equation by 2.

2y = 4x + 12

y = 2x + 6

Now that the equation is in slope-intercept form, you can find the slope. Recall that when an equation is in y = mx + b form, the slope is equal to m. Therefore, the slope of the line is 2.

Now, you may be wondering if there’s another way to find the slope of a line. You’re in luck! If you have no desire to rewrite the equation in slope-intercept form, you can determine the slope of a line when it is written as a linear equation, or in the form ax + by+ c = 0. In this scenario, the slope is equal to −.

The slope of a line in the form ax + by + c = 0 is equal to −

Let’s look at the previous question again.

EXAMPLE

What is the slope of the line 4x + 12 = 2y ?

Instead of rewriting the equation in slope-intercept form, let’s rewrite it in the linear form of an equation, or ax + by + c = 0. Start by subtracting 2y from both sides of the equation.

4x + 12 = 2y

4x − 2y + 12 = 0

Next, find the slope of the line by calculating −.

a = 4 and b = −

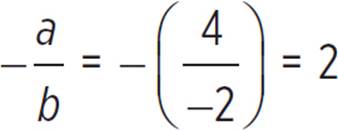
No matter how you crack it, the slope of the line is 2.

Now let’s walk through a question that tests your ability to identify visual representations of a linear equation.

EXAMPLE

Identify the graph that represents the line 2x + 3y = 6. Provide the slope, x-intercept, and y-intercept of the equation.

A)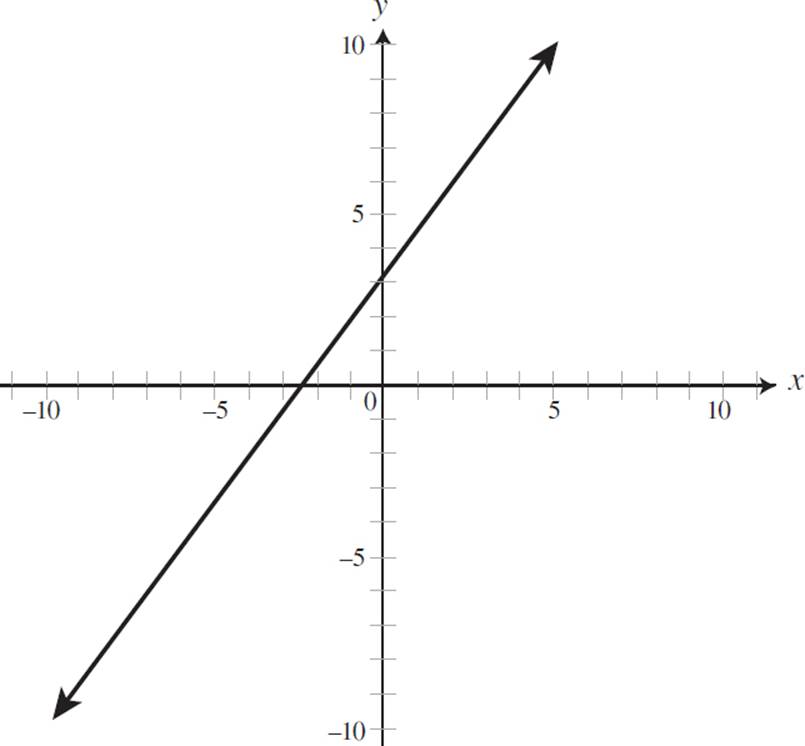

B)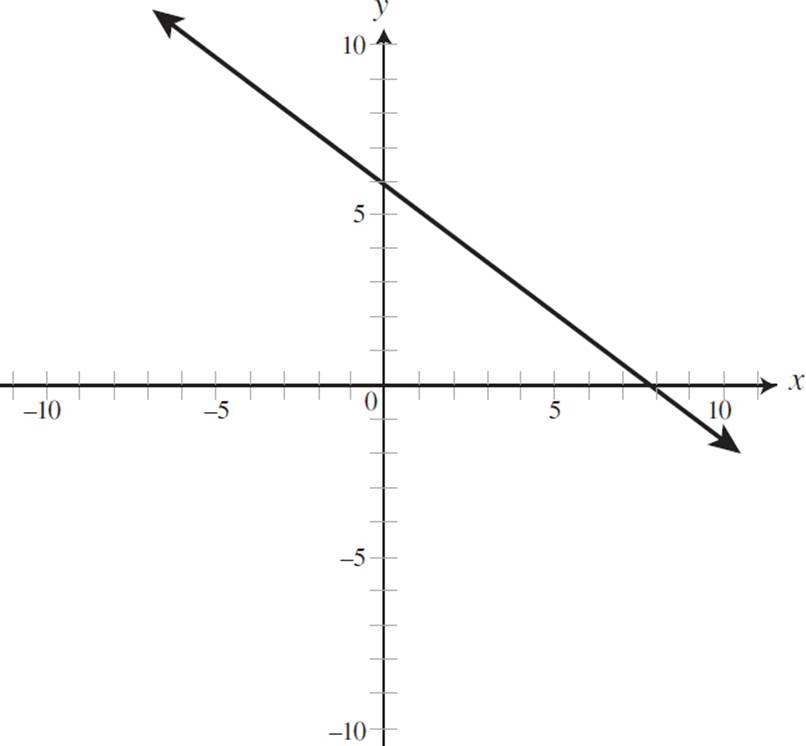

C)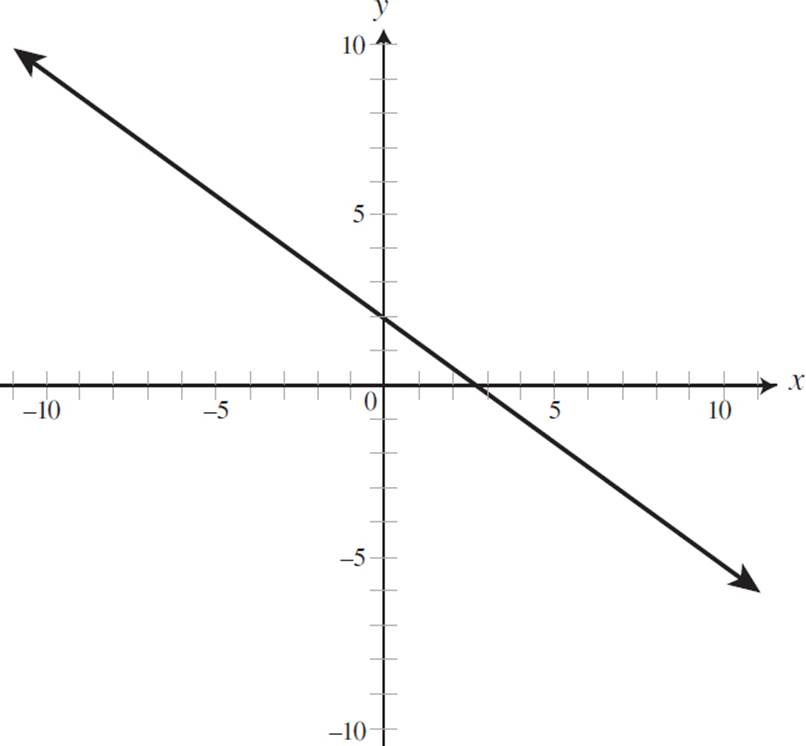

D)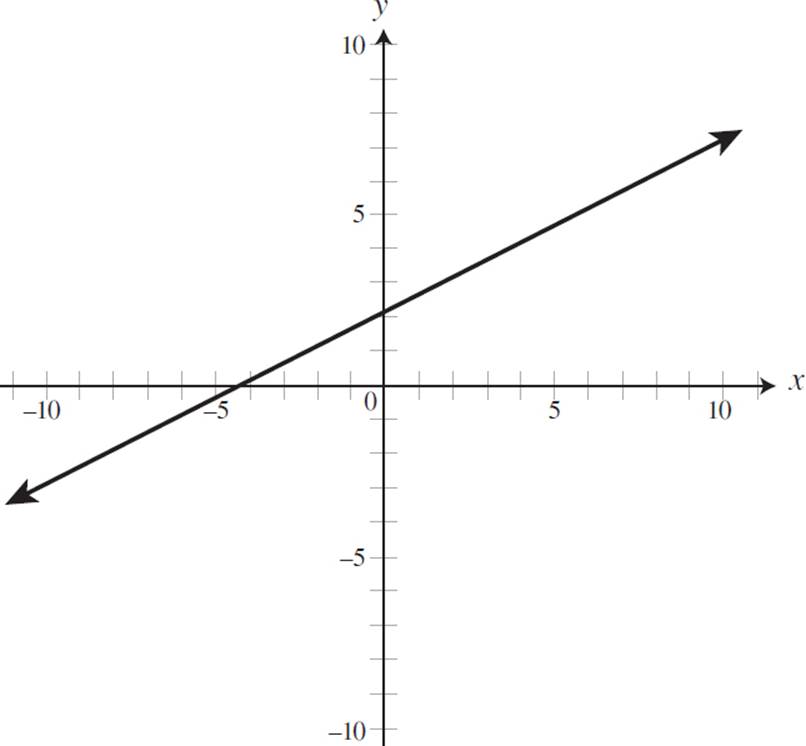

Where to begin? Start by putting the equation into y = mx + b form.

2x + 3y = 6

3y = −2x + 6

y = −x + 2

Now that the equation is in slope-intercept form, you can determine the slope and intercepts of the equation. Based on the equation, the slope of y = −x + 2 is −, and the y-intercept of the equation is (0, 2). Next, find the x-intercept by setting y = 0 and solving for x:

2x + 3y = 6

2x + 3(0) = 6

2x = 6

x = 3

Therefore, this equation has an x-intercept of (3, 0). Now that you have the slope and intercepts, you can identify the graph represented by the equation 2x + 3y = 6. Both (A) and (D) depict positive slopes and can thus be eliminated. Since we know that this equation has a y-intercept of 2, (B) can be eliminated. The only graph that represents an equation with a slope of −2/3, a y-intercept of (0, 2), and an x-intercept of (3, 0) is (C).

Here is how you may see slope on the ACT.

What is the slope of the line based on the equation 5x − y = 7x + 6 ?

F. −2

G. 0

H. 2

J. 6

K. −6