High School Algebra I Unlocked (2016)
Chapter 1. Fundamentals: Terminology and Properties
GOALS
By the end of this chapter, you will be able to:
•Identify and define the parts of mathematical expressions and equations
•Solve simple mathematical expressions with variables
•Apply the theory behind the associative, commutative, and distributive properties to solve mathematical expressions
•Identify equivalent expressions
•Compare and contrast exact, approximate, and estimated answers and solve problems related to these concepts
Lesson 1.1. Understanding Expressions
REVIEW
BEFORE BEGINNING THIS CHAPTER, YOU SHOULD BE FAMILIAR WITH:
•even and odd numbers
•positive and negative numbers
•basic mathematical operations, such as addition, subtraction, multiplication, and division
•numerical exponents and how to work with them in problems
•rounding decimals
•order of operations
When you were very young—let’s say around one year old—you began to develop language skills and learn how to communicate. Maybe your first word was “bug” or “bubble.” Eventually, you learned how to put sentences together in order to communicate your needs, and later on you figured out how to communicate more deftly in all kinds of scenarios. In short, you learned the rules of communication. And just as you developed linguistic skills to communicate in the world, you will need to develop and understand the basic language of math in order to conquer the world of algebra: the purpose of this book. This chapter takes a look at the fundamentals you need to know before advancing to the more complex topics this book covers. Let’s begin with expressions.
In math, an expression is a group of terms, which can be numbers, variables, or a combination of the two, grouped together to show, or express, a value. In an expression, terms are separated by mathematical operators, + or −. Mathematical operators × or ÷ can be used within terms. The following are mathematical expressions:
a2 + 4 4b − 8 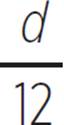 q
q
Let’s take a look at the anatomy of an expression. Notice that an expression consists of terms. In this expression, there are two terms: 4b and 8.
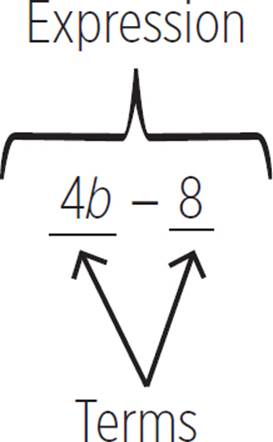
When an expression is set equal to a value, it is an equation. The following are mathematical equations:
a2 + 4 = 12 4b − 8 = c 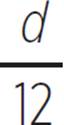 = 14
= 14
Now let’s break down one of the equations into its individual parts. Consider the equation 4b − 8 = c. As shown by the following figure, there’s a lot happening in this equation:
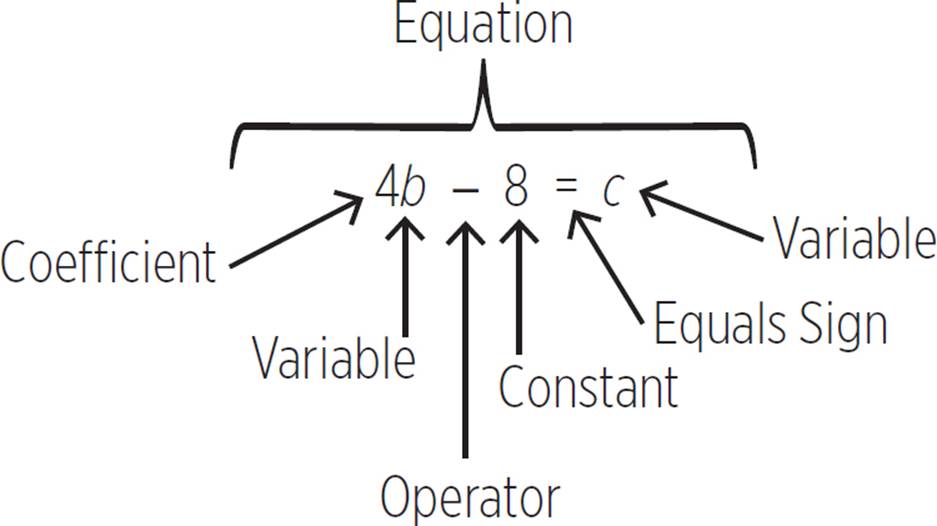
Some equations have even more parts than this one. The following table lists and defines the many parts an equation can have.
|
Term |
What Is It? |
|
coefficient |
A numerical constant in front of a variable that indicates the number of times the variable should be multiplied. For example, 4 is the coefficient in the term 4b, which is the same as saying 4 × b. |
|
constant |
A fixed numerical value that does not change; i.e., the value of a constant remains constant. In the equation 4b − 8 = c, 8 is the constant. |
|
exponent |
A value indicating the number of times the base number should be multiplied by itself. For example, the expression a2 indicates that a should be multiplied by itself two times: a2 = a × a. Likewise, the expression 43 = 4 × 4 × 4 = 64, as the exponent indicates that 4 must be multiplied by itself three times. |
|
expression |
A group of numbers, symbols, and operators that indicate a value. In the equation 4b − 8 = c, 4b − 8 is the expression. |
|
equation |
An equation has an equals sign, =, to show that two things have the same value. In an equation, the quantity to the left of the equals sign must be equal to the quantity to right of the equals sign. For example, 2 + 4 = 8 − 2 and 6 = 6. In the equation 4b − 8 = c, the value of 4b − 8 must equal the value of c. |
|
operator |
Symbols such as +, −, ×, or ÷ that indicate the necessary process to handle terms. For example, in the expression 2 + 3, the operator is +, indicating that you need to add the terms together. In the equation 4b − 8 = c, the operator is −, indicating that you need to subtract the terms. |
|
term |
A term can be a single number, variable, or a combination of the two. In an expression or equation, mathematical operators separate terms. In the equation 4b − 8 = c, the terms are 4b, 8, and c. |
|
variable |
A symbol for an unknown number. Variables are usually expressed as letters such as a, b, x, or y. In the equation 4b − 8 = c, the variables are b and c. |
When it comes to variables, there are two types that you should be aware of: independent and dependent. An independent variable is a variable whose variation does not depend on that of another variable. The independent variable is often known as the cause variable, as its value determines the value of another variable; it causes a change in the dependent variable. Conversely, the dependent variable is a variable whose value is determined by the value of the independent variable. The dependent variable is often referred to as the effect variable, as its value is the result of a change in the independent variable.
Independent and
dependent variables play a
role in almost all academic
arenas. For example, a
scientist may be interested
in testing the effect of
sleep on student test
scores. In this situation,
the independent variable
would be the amount of
sleep a student gets, and
the dependent variable
would be the test scores.
Notice that the amount of
sleep causes an effect on
the student test scores.
Consider the equation 4b − 8 = c. In this situation, b is the independent variable, and c is the dependent variable. Imagine that b = 2. The equation 4b − 8 = c would now be 4(2) − 8 = c, 8 − 8 = c, and 0 = c. Thus, setting the independent variable to b = 2 causes c = 0. See the cause-and-effect relationship?
Let’s try out a couple questions that deal with all of these mathematical terms.
EXAMPLE 
If a = 0, what is the value of a + 32 ?
Here you’re told that variable a has a value of 0, and you need to find the value of a + 32. Thus, you need to substitute 0 in for a in the expression a + 32.
a + 32 = 0 + 32
= 0 + 9
= 9
That’s all there is to it—the correct answer is 9!


Below is your first
“Locksmith” sample
question. You’ll see these
example SAT and ACT
problems throughout
the book, and we’ve
included additional
practice questions online.
Register your book (see
this page) to gain access
to this content and more!

Here is how you may see math terminology tested on the ACT.
If p is an odd integer, which of the following must also be an odd integer?
A. p + 1
B. ![]()
C. p + 2
D. 2p
E. p − 1
Now let’s take a look at the same expression in a different scenario.
EXAMPLE 
If a = −1, what is the value of (a + 3)2 ?
This expression is similar to that in the previous question, but here a = −1, and the expression is (a + 3)2. Based on the order of operations, start by setting a = −1 and finding the value inside the parentheses:
(a + 3)2 =
(−1 + 3)2 =
(2)2 =
Finally, simplify the result:
(2)2 = 4
Thus, you will find that when a = −1, the value of (a + 3)2 is 4.

When you have to perform
multiple operations on
a single expression,
use PEMDAS to guide
the order in which you
perform the operations:
Parentheses
Exponents
Multiplication
Division
Addition
Subtraction