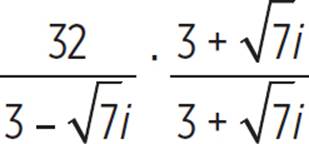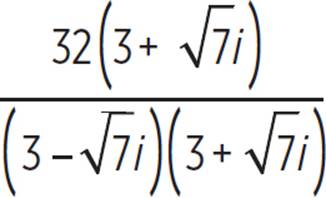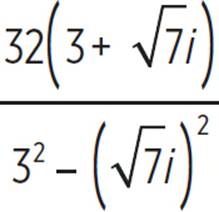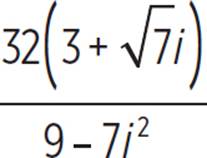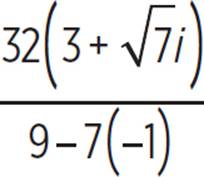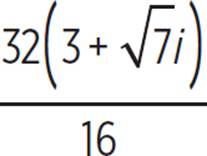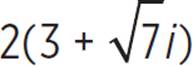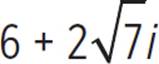High School Algebra II Unlocked (2016)
Chapter 1. Complex Numbers and Polynomials
GOALS
By the end of this chapter, you will be able to
•Perform arithmetic operations with complex numbers
•Perform arithmetic operations with polynomials
•Use polynomial identities to solve for certain quantities, find Pythagorean triples, and factor polynomials
•Graph polynomial functions and derive polynomial equations from given graphs
•Factor higher-degree polynomials completely, into any real- and/or imaginary-number roots
•Create and interpret polynomial functions and their graphs to represent and explain real-world relationships
Lesson 1.1. Complex Numbers
REVIEW
COMMUTATIVE PROPERTY OF ADDITION
a + b = b + a
ASSOCIATIVE PROPERTY OF ADDITION
(a + b) + c = a + (b + c)
DISTRIBUTIVE PROPERTY
a • (b + c) = a • b + a • c
POLYNOMIAL IDENTITIES
(a + b)(c + d) = ac + ad + bc + bd
(a.k.a. FOIL)
(x + a)(x + b) = x2 + (a + b)x + ab
(a.k.a. FOIL with x-terms)
(a + b)2 = a2 + 2ab + b2
(a.k.a. square of a sum)
a2 − b2 = (a + b)(a − b)
(a.k.a. difference of squares)
a3 − b3 = (a − b)(a2 + ab + b2)
(a.k.a. difference of cubes)
a3 + b3 = (a + b)(a2 − ab + b2)
(a.k.a. sum of cubes)
What is 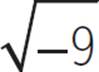 ? In other words, what number squared equals −9? If you square 3, the result is 9, and if you square −3, the result is also 9, because a negative multiplied by a negative is a positive. It seems like
? In other words, what number squared equals −9? If you square 3, the result is 9, and if you square −3, the result is also 9, because a negative multiplied by a negative is a positive. It seems like 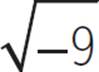 doesn’t exist….but it does, in mathematics, as an imaginary number.
doesn’t exist….but it does, in mathematics, as an imaginary number.
The imaginary number i is defined as the square root of −1, so i2 = −1.
Using imaginary numbers will allow you to solve problems that you’ve never before been able to solve. Now we can solve for 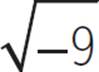 , which can be rewritten as
, which can be rewritten as 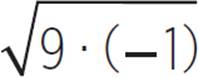 , or
, or 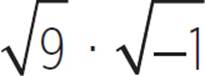 , which equals 3i.
, which equals 3i.
A complex number is a number in the form a + bi, where a and b are both real numbers.
This means that a complex number includes both a real-number component (a) and an imaginary-number component (bi). The number −5 + 2i is a complex number. The imaginary number 3i, which we mentioned above, is also a complex number—just one where the value of a in a + bi is 0.
All real numbers are
also complex numbers,
just with b = 0 in
the form a + bi.
The set of complex numbers includes all real numbers, all imaginary numbers, and all sums of real and imaginary numbers.
We can graphically represent complex numbers as points or vectors on a special complex number plane, which looks kind of like a real number plane (standard (x, y) coordinate grid) but with real numbers on the horizontal axis and imaginary numbers on the vertical axis. The point representing a complex number is plotted in alignment with its real-number component on the horizontal axis and its imaginary-number component on the vertical axis. The vector representing the same complex number is the vector from the origin to that point.

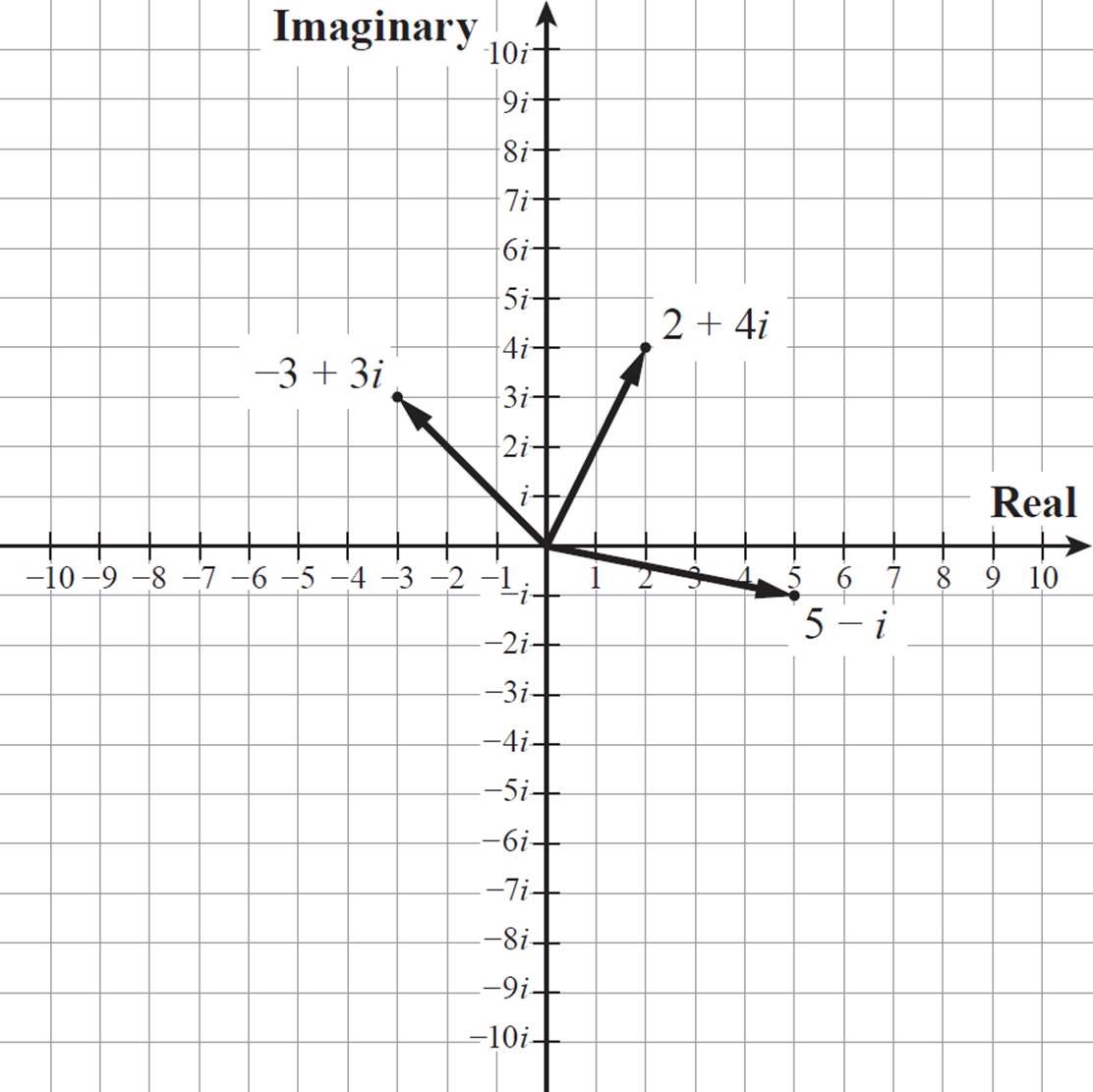
Show 2 + 4i, 5 − i, and −3 + 3i on a complex number plane.
The complex number 2 + 4i consists of a positive 2 and a positive 4i, so we’ll draw a vector from the origin to the point that aligns with 2 on the real-number axis and 4i on the imaginary-number axis.
The complex number 5 − i aligns with 5 on the real-number axis and −i on the imaginary-number axis.
The complex number −3 + 3i aligns with −3 on the real-number axis and 3i on the imaginary-number axis.
The vectors and points representing 2 + 4i, 5 − i, and −3 + 3i are shown on the complex number plane below.

We can add complex numbers on the complex number plane by combining vectors. Start from the point of the first complex-number addend, and use the direction and length of the second complex number vector to find the point representing the sum.

Here is how you may see complex numbers on the ACT.
In the complex numbers, where i2 = −1, which of the following is equal to the result of squaring the expression (i + 5) ?
A. 5i
B. 25i
C. 10i + 24
D. 5i − 25
E. i + 25

What is the sum of 2 + 4i and 5 − i ?
These vectors are shown in Example 1. Place the vector representing 5 − i, or the direct path that travels 5 units to the right and 1 unit down, starting at the end of the vector representing 2 + 4i.
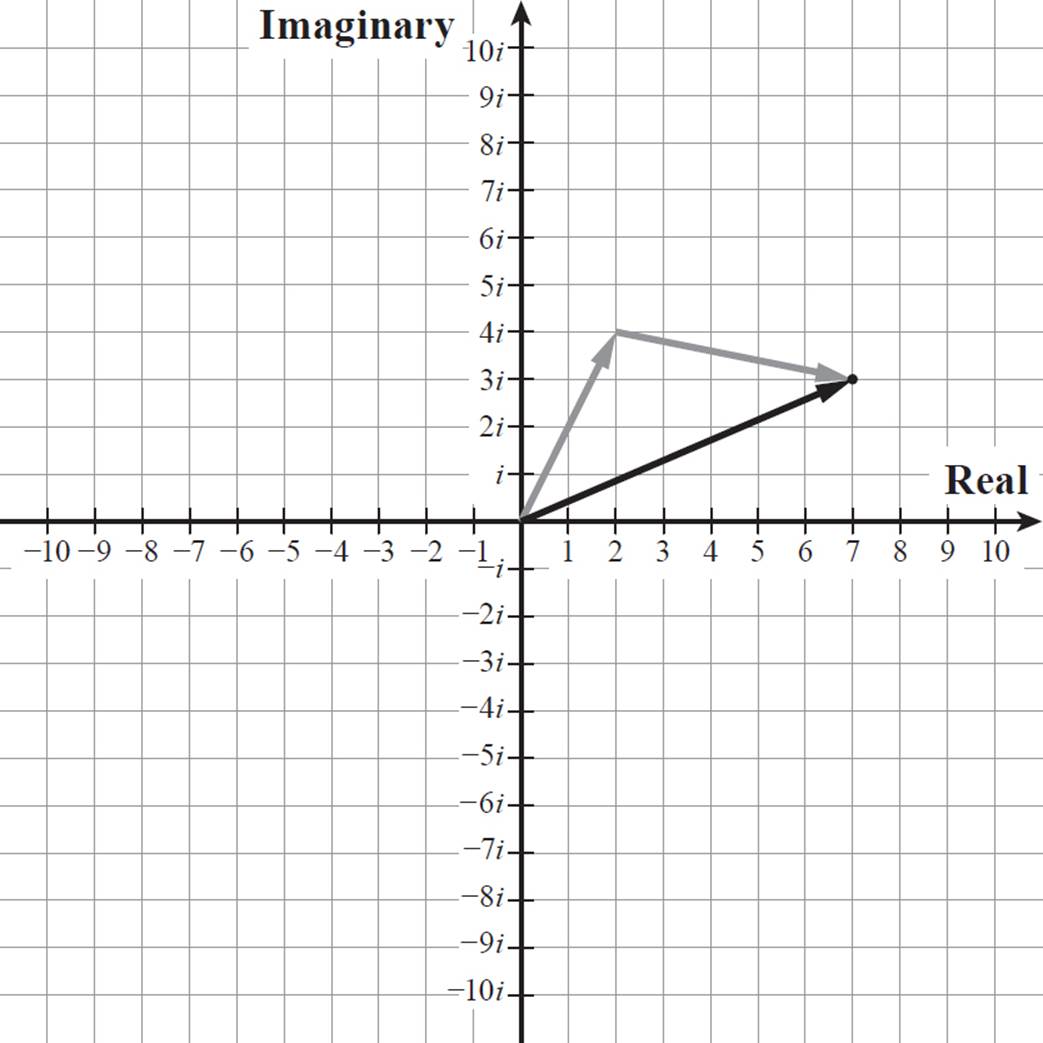
The sum is the point where the second vector ends, or 7 + 3i. The vector 7 + 3i, which moves 7 units to the right and 3 units up, is also shown on the graph.
We can also solve for the sum algebraically, as we would with real numbers. The commutative, associative, and distributive properties apply to all complex numbers.
|
2 + 4 i + 5 − i |
|
|
2 + 5 + 4 i − i |
Commutative property |
|
(2 + 5) + (4 i − i) |
Associative property |
|
(2 + 5) + (4 − 1)(i) |
Distributive property |
|
7 + 3 i |


Find the product of and simplify the expression below.
(i − 4)(2i + 9)
|
2i2 + 9i − 8i − 36 |
Expand using FOIL. |
|
2i2 + i − 36 |
Combine like terms, 9i − 8i. |
|
2(−1) + i − 36 |
Substitute −1 for i2. |
|
−2 + i − 36 |
Multiply 2(−1). |
|
i − 38 |
Combine like terms, −2 − 36, using the commutative property of addition. |


Fully simplify the expression below.
(8 + 10i)[12 − 2i − (7 − 6i)]

The expression (8 + 10i)[12 − 2i − (7 − 6i)] is equal to 82i.


Translate the words into an algebraic expression then expand and simplify.
|
(i + 5)2 = (i + 5)(i + 5) |
Squaring the expression means multiplying it by itself. |
|
= i2 + 5i + 5i + 25 |
Expand using the distributive property (FOIL). |
|
= i2 + 10i + 25 |
Combine like terms, 5i + 5i. |
|
= −1 + 10i + 25 |
Substitute −1 for i2. |
|
= 10i + 24 |
Combine like terms, −1 + 25. |
The correct answer is (C).

Multiplying by the
conjugate of the
denominator is the
same method you
would use to simplify
a fraction that contains
the sum of a rational
number and a square
root in its denominator,
such as 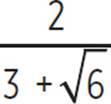 .
.
Sometimes, the result of operations involving complex numbers is a fraction that has a complex number in the denominator. As you may recall from working with square roots in previous courses, the fraction is not fully simplified until the denominator is rational. Having an imaginary number in the denominator is anything but rational.
In order to simplify the denominator, we multiply both the numerator and denominator by the conjugate of the denominator. For example, to put 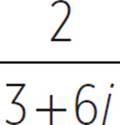 in standard form, we multiply both the numerator and denominator by (3 − 6i). We do this because it produces a difference of squares in the denominator, including i2, which is equal to the rational number −1. Once we replace i2 with −1, the denominator becomes a real number, and the entire rational expression can be rewritten in the standard form for a complex number, a + bi.
in standard form, we multiply both the numerator and denominator by (3 − 6i). We do this because it produces a difference of squares in the denominator, including i2, which is equal to the rational number −1. Once we replace i2 with −1, the denominator becomes a real number, and the entire rational expression can be rewritten in the standard form for a complex number, a + bi.

Simplify the expression 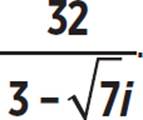
This fraction has an imaginary number, as well as a square root, in the denominator. To rewrite it in standard form, we must multiply both the numerator and the denominator by the conjugate of 3 − 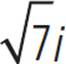 , which is 3 +
, which is 3 + 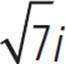 .
.
|
|
|
|
|
Multiply the numerators and the denominators. |
|
|
Rewrite the denominator as a difference of squares. |
|
|
Find each squared term. |
|
|
Substitute −1 for i2. |
|
|
Simplify the denominator. |
|
|
Simplify the fraction by dividing the numerator by the denominator, 16. |
|
|
Distribute to multiply through. |