High School Algebra II Unlocked (2016)

Lesson 5.2. Logarithms

REVIEW

Rules of exponents, for real number b, b > 0, and rational numbers m and n:

b¹ = b

b⁰ = 1

b⁻ⁿ = 1/bⁿ

b^m · bⁿ = b^{m + n}

(b^m)ⁿ = b^mn

b^m/bⁿ = b^{m − n}

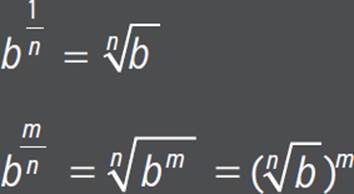
b/0 is undefined.

A logarithm is the inverse operation to exponentiation (raising a number to an exponent). The logarithm undoes the work of the exponential expression.

If y = b^x, then log_by = x. Likewise, if log_by = x, then y = b^x.

So, the logarithm is the exponent to which the base must be raised to produce the value y in logby. For example, log₄64 is the exponent to which 4 must be raised to produce 64. The equation log₄64 = x can be rewritten as 4x = 64. Because 4 cubed is equal to 64, 4^x = 4³, and x = 3.

If the same base is raised to an exponent on either side of the equation (without any other terms or factors), then the exponents are equal: If b^x = b^y, then x = y.

The term “log” is
short for “logarithm,”
and the b in log_by
is its base, just as b
is the base in b^x.

Evaluate each of the following expressions, where they exist.

Set each logarithm equal to x and rewrite the equation in exponential form, then solve.

The number 1 could
be rewritten as any
base to the power of
0, such as 5⁰, but for
our solution process
8⁰ is most helpful.

There is no power of 2 that would produce −4. The expression log₂−4 is undefined.

There is no power of 6 that results in 0. The expression log₆0 is undefined.

If you are tempted
to try letting
x = 0, remember
that 6⁰ = 1, not 0.

For any positive real number b, where b ≠ 1:

log_bb = 1

log_b1 = 0

log_b0 is undefined.

log_bc is undefined if c is negative.

log_bbⁿ = n

log_b(1/bⁿ) = −n

In the last step of solving each of the equations we wrote for Example 3, we set the exponents of matching bases equal to one another: If b^x = b^y, then x = y. However, what we were really doing at each of those moments was taking the logarithm of both sides of the equation.

It’s important to use the same base on both sides when taking the logarithm of both sides of an equation. As with any other operation applied to an equation, you must do exactly the same thing to both sides, to maintain the equality.

In Example 3, all logarithms that existed had integer values. However, exponents are sometimes fractions.

Remember, the
logarithm is the
inverse operation to
exponentiation. When
solving an equation,
you typically apply the
inverse operation of
those already applied
to the variable. When
you see x + 4 = 9, you
use subtraction (of 4)
on both sides, because
it is the inverse of
the addition shown.
Likewise, when you see
3^x = 3⁷, you should take
the logarithm (base 3)
of both sides, to undo
the exponentiation.

Find the value of each of the following expressions.

If log₁₆4 = x, then 16^x = 4. The square root of 16 is 4: = 4, which can also be written as 16^1/2 = 4. Substitute 16^1/2 for 4 in 16^x = 4.

So, log₁₆4 = 1/2.

If log₉27 = x, then 9^x = 27. We can write both sides of this equation as exponential expressions with base 3.

So, log₉27 = 3/2.

To check our work, we can rewrite the equation log₉27 = 3/2 as 9^3/2 = 27. The numerator in the fractional exponent acts like a whole-number exponent, cubing 9. The denominator of 2 represents a square root. The expression 9^3/2 can be written either as or as .

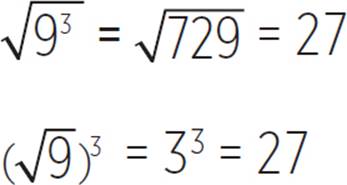
As you become more familiar with logarithms, you may not need to write an equation with a variable (such as x) to evaluate numerical logarithms. Just ask yourself, “What exponent, when applied to that base, will give the number shown?” However, sometimes you must solve equations containing logarithms that already include one or more variables.

The reason you can
write the expression
9^3/2 as either (9³)^1/2 or
(9^1/2)³ is because both
of these represent 9
raised to the power
of (3 · 1/2). By the
commutative property
of multiplication,
3 · 1/2 is equal to
1/2 ⋅ 3, so
9^{3 · 1/2} = 9^{1/2 · 3}.

Here is how you may see logarithms on the ACT.

Which of the following ranges of consecutive integers contains the value of the expression log₈(8^11/3)?

A. 0 and 1

B. 1 and 2

C. 2 and 3

D. 3 and 4

E. 7 and 8

If log_{d + 6}625 = 4, what is the value of d?

Write an equation using the definition of logarithm, then solve for d.

Solve the following equation for x.

log₂(x² − 2x) − 1 = 2

First, add 1 to both sides to put the equation in the form log_bm = n, which can be rewritten as bⁿ = m. This notation is different from how we referred to this earlier (log_by = x and b^x = y), but that’s just because x is already being used. Any letter can be used as a variable, as long as it and its relationship to everything else is consistent throughout that equation.

The solutions to log₂(x² − 2x) − 1 = 2 are x = −2 and x = 4. If you substitute either value into the equation, you get log₂8 − 1 = 2, which simplifies to 3 − 1 = 2, a true equation.

The parentheses tell
us that the entire
expression x² − 2x
is included in the
logarithmic expression,
whereas the −1 is not.

What is the value of k in the equation below?

3^log₃^2k = 9

We are given an exponential equation (with a funny looking exponent, but it is still just an exponent of 3), so we can use the definition of logarithm to rewrite the relationship as a logarithmic relationship.

log₃9 = log₃2k

This is the same as
taking the logarithm,
base 3, of both sides of
the equation 3^log32k = 9.

For any positive real number b, where b ≠ 1, b^logbx = x.

Because the expression log_bx represents the exponent to which b must be raised to get x, raising b to that exponent is equal to x.

Using this identity
as a shortcut in
Example 7 would have
brought us directly
to the second-to-last
line in the solution
process, 2k = 9.

The expression log₈(8^11/3) is in the form log_bbⁿ, so it is equal to n, the exponent 11/3.

log₈(8^11/3) = 11/3

The value of 3 is between 3 and 4, so the correct answer is (D).

SPECIAL LOGARITHMS

Logarithms can have any positive number for a base, but those with bases of 2, e, or 10 are especially useful.

A logarithm of base 2 is called a binary logarithm and is commonly used in computer science. Finding a binary logarithm means determining what power of 2 produces the given number. For example, log₂32 = 5 and log₂(1/8) = −3.

A logarithm of base e is called a natural logarithm. The constant e is an irrational number with a value of about 2.718. Natural logarithms are usually written using the notation ln instead of log-base-e: log_ex = lnx.

This number 2.718….
probably seems rather
random or arbitrary,
but there are several
ways in which e
is mathematically
meaningful. For
example, it is the limit
of (1 + 1/n)ⁿ as n
approaches infinity.

Simplify the expression lne^2x.

The base is e, so by the definition of logarithm, lne^2x is the exponent to which e must be raised in order to get e^2x. The answer is 2x.

You can also view this as a version of the rule log_bbⁿ = n: log_ee^2x = 2x. Or, you can always go back to basics and use the definition of a logarithm to rewrite the expression in an exponential equation you can then solve.

A logarithm of base 10 is called a common logarithm. It is so common that if you see a logarithm written without a base, such as log5, you can generally assume that it is a common logarithm (log₁₀5 in this case). Common logarithms are often used to create logarithmic scales, such as the Richter scale.

A logarithmic scale uses logarithms of numbers instead of the numbers themselves for the breakdown of measurements, and it is especially helpful when representing a wide range of numbers. A difference of 1 unit on a logarithmic scale means multiplication or division by a factor of 10, so a 6.0-magnitude earthquake on the Richter scale is 10 times as strong as a 5.0-magnitude earthquake and 100 times as strong as a 4.0-magnitude earthquake.

A video game company posted the following profits for each of its first six years in business.

Graph the company’s first six years’ profits using a linear scale and using a logarithmic scale.

The profits range from 2000 to 10,000,000 dollars, so our y-axis should show values from 0 to at least 10,000,000. For a linear scale, the increments are evenly spaced and valued, so let’s use tick marks of 1,000,000.

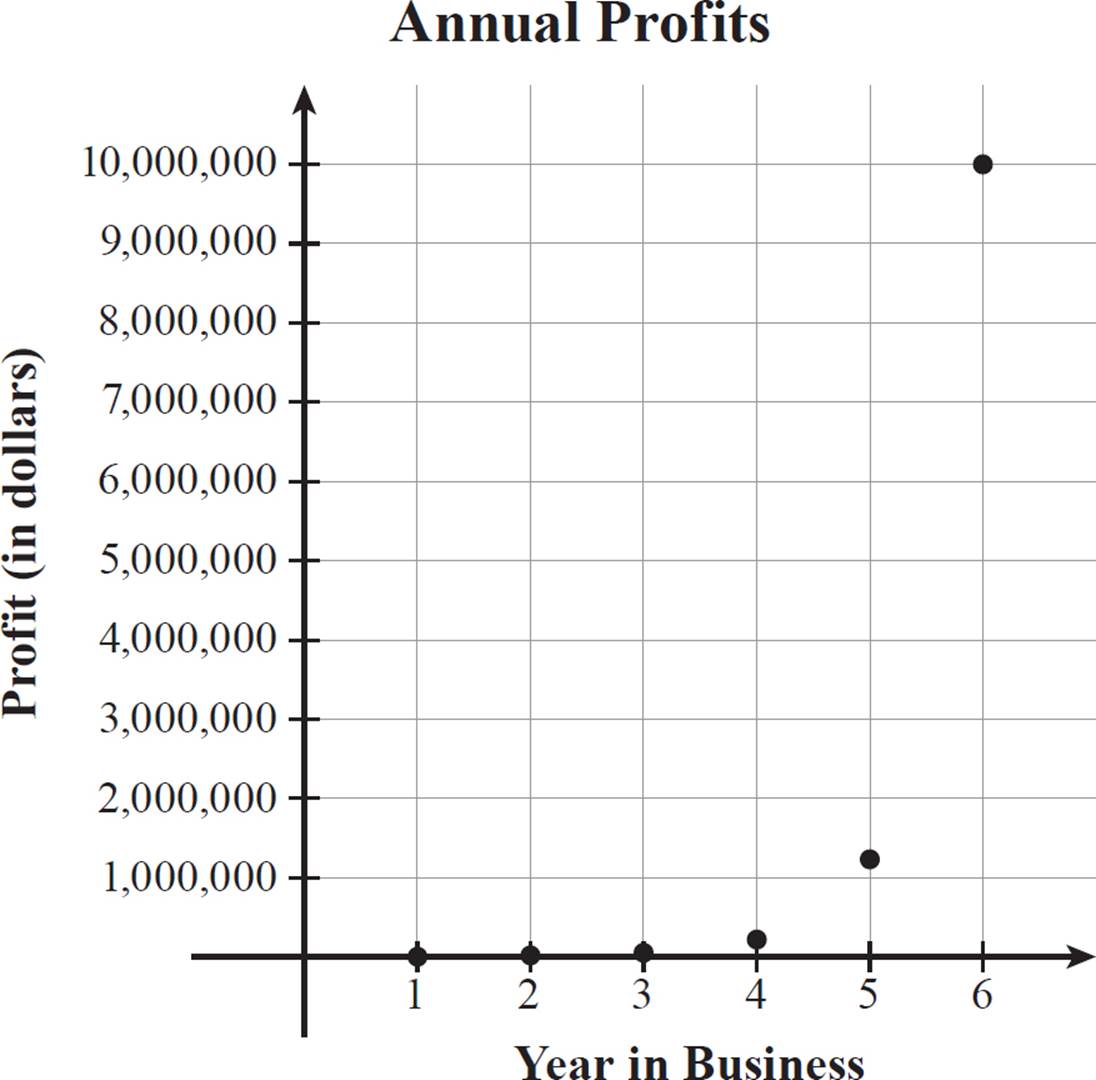
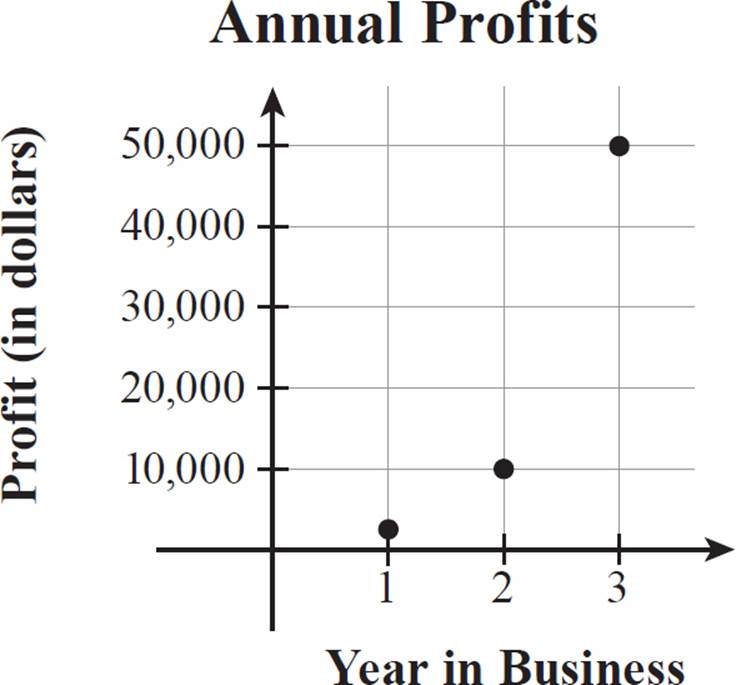
Although this gives some sense of the large growth in profits, it does not show the first few years’ profits in much detail. If we plotted just the first three years with a linear scale of 0 to 50,000, we would have the graph below.

The “log” button
on your calculator
calculates the
common logarithm,
automatically
assuming a base of 10.

This graph clearly shows the relationship between the first three data points, but to include the other three data points using this scale, the graph would have to be 200 times as tall! We don’t have enough paper for that. It’s time to turn to a logarithmic scale.

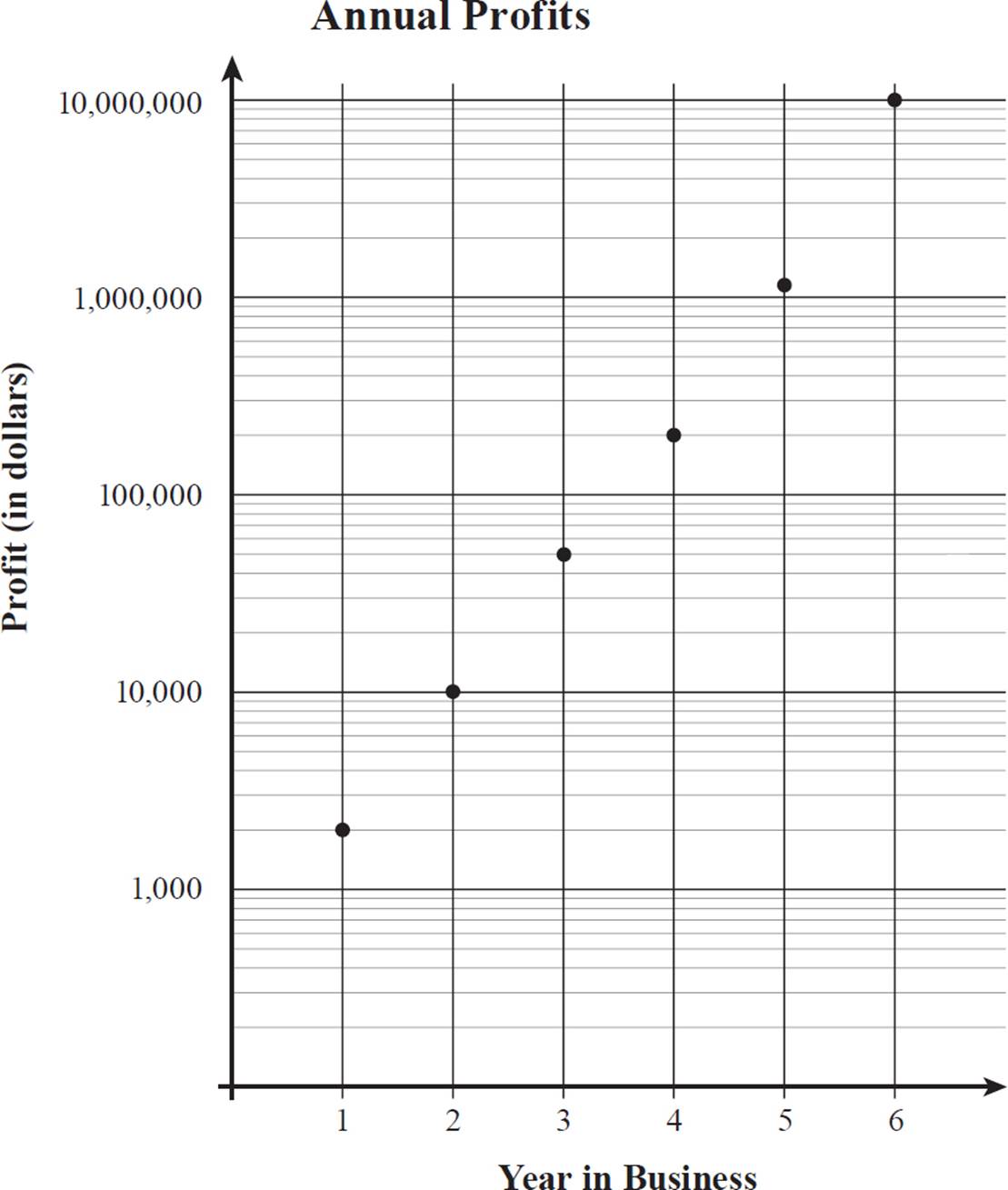
A common logarithm is the exponent to which 10 must be raised to produce the given number. So, log₁₀1000 = 3 and log₁₀10,000,000 = 7. All of our data points will be between 3 and 7 using the common logarithm. Use your calculator to find each logarithmic value, rounded to the nearest tenth. This gives us the data points for this graph: (1, 3.3), (2, 4.0), (3, 4.7), (4, 5.3), (5, 6.1), and (6, 7.0). Here is a graph of the company’s profits using a logarithmic scale.

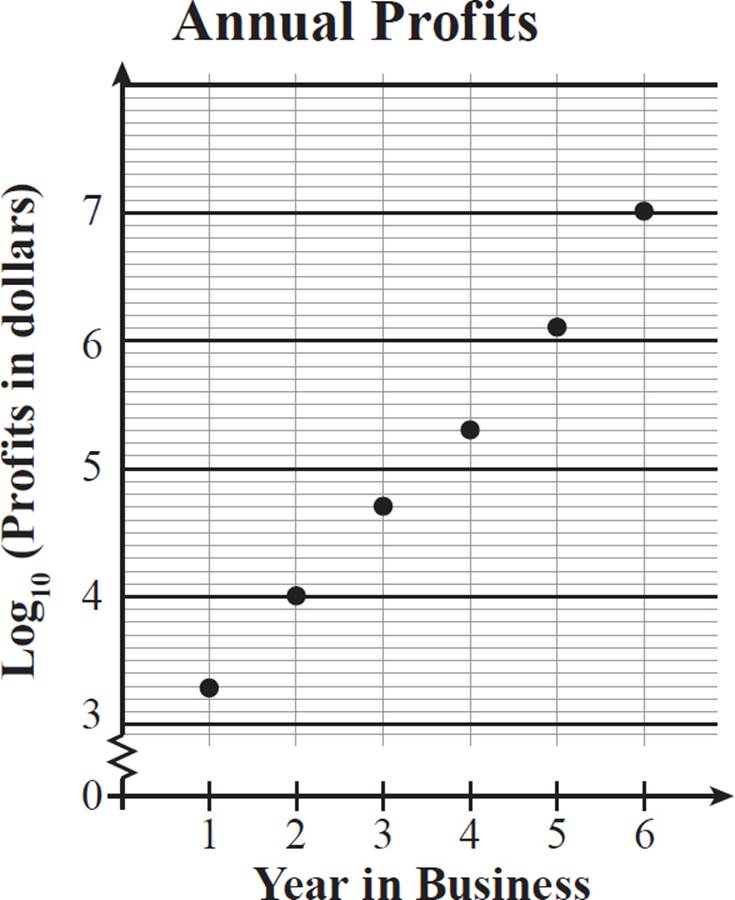
Graphs are often presented in a logarithmic scale but using the actual values rather than the log values as axis labels. For evenly spaced log intervals, the actual value intervals take up decreasing amounts of space between whole-number log values, as shown in the scale below.

The logarithmic values are the exponents of 10 that produce the actual values. Evenly spaced increments of logarithmic values shown in our last graph of Annual Profits must be shown as intervals of varying sizes, as in the scale above, in order for us to label our y-axis with regular increments of actual profit values.

The x-axis of our
graph is linear
because the data
points have a very
simple set of evenly
spaced x-values,
{1, 2, 3, 4, 5, 6}.
Sometimes graphs use
a logarithmic scale on
the horizontal x-axis,
with either a linear or
a logarithmic scale on
the vertical axis. The
best scales to use for
representation depend
on the given data set.