Idiot's Guides: Algebra I (2015)
Part III. Variations on the Line
Those detective stories I love may start out with a straight path to a solution, but of course, that doesn’t stay straight or simple for long. Soon things crop up that are a little out of the ordinary, that are exceptions to the rule, or perhaps things just get a little more complicated with another crime or another suspect showing up.
In Part 3, we’re going to look at some variations on that linear path we started on. The first bend in our road will be absolute value functions, whose graphs look like lines that took a sharp turn, and whose solutions demand that we consider multiple possibilities. We’ll look at vertical and horizontal lines, which bend the rules we learned for lines, and then we’ll explore systems of linear equations, which bring together two perfectly reasonable equations and ask us to figure out when they can both be true.
Chapter 8. Absolute Value Functions
In This Chapter
![]()
· Solving absolute value equations
· Solving absolute value inequalities
· Solving problems with absolute value equations and inequalities
If it’s a little less than 2,800 miles from New York to Los Angeles, how far is it from Los Angeles to New York? It’s also a little less than 2,800 miles, of course. It doesn’t matter whether you’re traveling east to west or west to east; the distance is the same. In algebra, when you think about the real numbers on a number line, direction usually does matter. Moving from -4 to 7 is thought of as a positive move, but 7 to -4 is looked upon as negative. When direction doesn’t matter, you’re talking about absolute value. In previous chapters, we’ve talked about the absolute value of a number, but in this chapter, we’ll look at what happens when an equation or inequality involves the absolute value of a variable or expression.
Understanding Absolute Value
The absolute value of a number is its distance from 0 without regard to direction. A number and its opposite have the same absolute value, because they are the same distance from zero, but in different directions.
![]()
DEFINITION
Absolute value is a measure of distance, without regard to direction. It tells the size, or magnitude, of the number without considering its sign.
When a variable is placed inside absolute value signs, it’s more difficult to interpret, because you don’t know the value of the variable. You don’t know the sign of the number, but rather its distance from zero. If you say |x| = 4, you accept both 4 and -4 as possible values of x, because both are four units from zero.
Expressions find their way inside the absolute sign when you think about things like the distance from New York to Los Angeles. East to west, or west to east, it’s the absolute value, not the direction, you care about. If x is a number 7 units from 9, then you calculate 9 − x or x − 9 to get the distance between x and 9. One will give you 7 and one will give you -7. Without knowing the value of x, you can’t know which is positive and which is negative, but you don’t really care about the direction. What you’re saying is |x − 9| = |9 − x| = 7. Either subtraction gives you a number that has an absolute value of 7.
When you’re trying to translate a statement about distances into an absolute value equation, first find the distance. This is what the absolute value will equal. If Jennie is visiting a town 100 miles from Omaha, Nebraska, the distance is 100 miles, and the equation is going to have the form |some calculation| = 100. If y is a number 8 units from 3, the distance is 8 and the equation will have the form |some calculation| = 8. Next look at the calculation you need to do. Define a variable if it hasn’t already been done for you. Usually in these cases the calculation is a subtraction. |y − 3| = 8 or |3 − y| = 8 will both work.
![]()
CHECK POINT
Write an absolute value equation for each sentence.
1. A number n is 6 units away from 9.
2. The number -4 is 10 units away from a number t.
3. The distance between x and 5 is 12 units.
4. Twice the distance between y and -4 is 12.
5. The distance between z and 12 is 4 more than z.
Write a sentence that describes the relationship in the equation.
6. |x − 7| = 3
7. |t − (−2)| = 9
8. |8 − y| = 11
9. 5|x − 4| = 20
10. |z − 7| = z − 3
Understanding absolute value and being able to write absolute value equations are important steps, but equations aren’t especially helpful unless you can solve them. Solving absolute value equations is a lot like solving linear equations, but not quite the same. Let’s have a look at the similarities and differences.
Solving Absolute Value Equations
We talk a lot about the absolute value of a number when we learn to work with integers, but it’s also possible to have a variable expression inside an absolute value sign. If you write |x| = 4, that’s not quite the same as saying x = 4. It’s true that replacing x with 4 makes the statement true. The number 4 has an absolute value of 4, but it’s also true that the number -4 has an absolute value of 4. The equation |x| = 4 has two solutions, x = 4 and x = −4.
Most equations that have a variable expression inside absolute value signs will have two solutions, so when you encounter one of these absolute value equations, expect that. Look for the two solutions by translating the absolute value equation into two equations that do not involve absolute value. Take the expression inside the absolute value signs and show that it could have a positive value or a negative value. The absolute value equation |x| = 4 becomes x= 4 or x = −4. The absolute value equation |4x − 3| = 9 gets rewritten as 4x − 3 = −9.
Once you have rewritten the absolute value equation as two separate equations, you can solve them as you normally would.
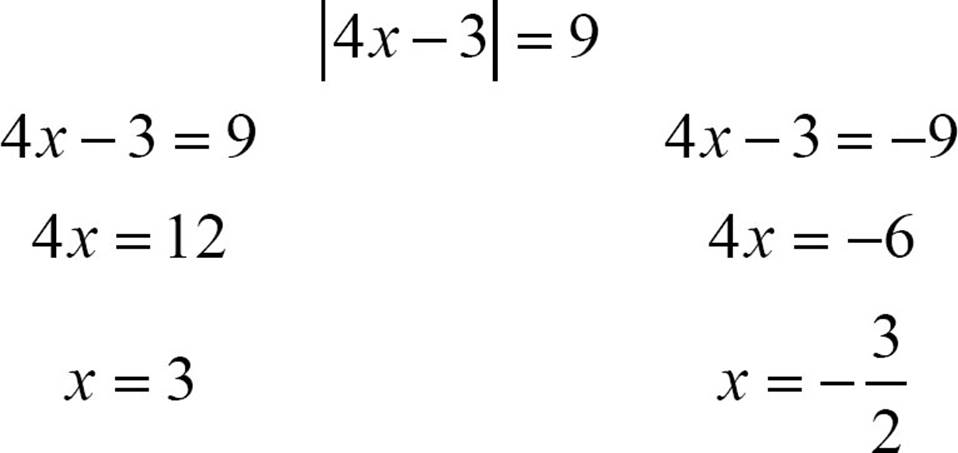
This gives two possible solutions.
To solve |3x − 7| = 5, treat it as though it were two equations, one that says 3x − 7 = 5 and one that says 3x − 7 = −5. Solve both equations.
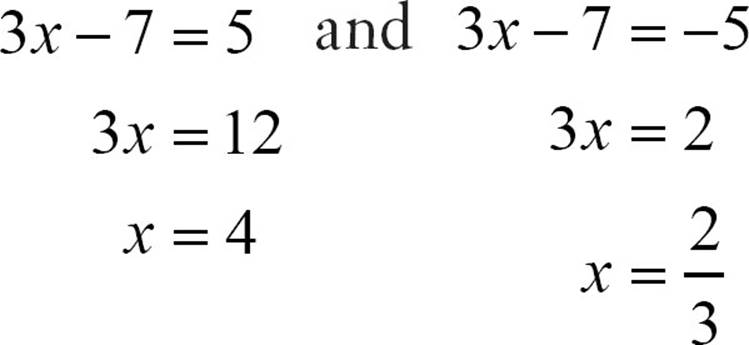
![]()
ALGEBRA TRAP
Not every absolute value equation has opposites as its solutions. Write the two equations that are equivalent to the absolute value statement, and don’t just solve one and assume the other will give you the opposite. Take the time to solve them both, independently.
![]()
CHECK POINT
Solve each absolute value equation. Be sure to check your answers in the original equation.
11. |3x − 7| = 2
12. |2t + 5| = 3
13. |y − 8| = 1
14. |x − 13| = 5
15. |11 + 8x| = −17
16. 2|3x − 1| = 14
17. |2y − 4| + 7 = 9
18. 5 − 3|x + 1| = −4
19. 2 + 7|4 − 3x| = 16
20. |4x − 5| = x
Solving Absolute Value Inequalities
Like absolute value equations, inequalities involving absolute values need special treatment. If you write |x| < 4, it’s not the same as writing x < 4. On the positive side, x might certainly be any number between 0 and 4, but what about negative numbers? Can x be replaced with any negative number to get a true statement? It doesn’t take much trying to find out the answer is no. Numbers between 0 and -4 will work, but numbers less than or equal to -4 will make the statement false. The absolute value of -5 is not less than 4. The inequality |x| < 4 is equivalent to the compound inequality −4< x < 4. These are the values of x that are less than 4 units from 0.
If you change the direction of the inequality, however, so that you have |x| > 4, the values of x that make true statements are those greater than 4 or less than -4. Once again, the absolute value inequality becomes a compound inequality, but this time, it’s an or inequality, x < −4 or x > 4, rather than an and inequality.
To remember how to change an absolute value inequality to the correct compound inequality, use the mnemonic device GreatOR/Less ThAND. (It’s a deliberate misspelling.) If the absolute value is greater than a number, make an or inequality. If the absolute value is less than a number, make an and inequality.
To solve an absolute value inequality, translate the absolute value inequality to a compound inequality. If the absolute value is greater than a constant, use an or compound. If the absolute value is less than a constant, use an andcompound.
|
GreatOR: |
|expression| > constant |
expression > constant or expression <− constant |
|
Example: |
|3x − 7| > 5 |
3x − 7 > 5 or 3x − 7 < −5 |
|
Less ThAND: |
|expression| < constant |
−constant < expression < constant |
|
Example: |
|4x + 5| < 17 |
−17 < 4x + 5 < 17 |
![]()
Check Point
Solve each absolute value inequality. Graph the solution set on the number line.
21. |6x − 7| > 5
22. |1 − 6x| < 7
23. |5y + 2| ≤ 12
24. |7z − 11| ≥ 3
25. |8a + 3| ≤ 19
26. |5 − 4x| < 21
27. |16p + 22| ≥ 6
28. |9t + 5| ≤ −2
29. |2x + 10| < 32
30. |7y − 23| ≥ 0
Modeling with Absolute Value
When do you need absolute value to solve a problem? Your first look at the information in a problem may suggest an equation to solve the problem, but a little more thought may tell you that there is more than one possible answer, and that’s the clue that you may need an absolute value equation or inequality.
Absolute value problems are usually about distance in some way. It may be the actual distance between two places, or the distance between points on a number line, or an amount of a change. Whatever the context, the direction isn’t known, or isn’t significant, so absolute value is appropriate.
When the two points in the coordinate plane have the same x-coordinate, they sit on the same vertical line. If two points have the same y-coordinate, the points sit on a horizontal line. The points (3, 0) and (-12, 0) both sit on the horizontal line called the x-axis, and you can think about them as though they were points on the number line. The points (4, -7) and (4, 9) both lie on the vertical line x = 4, and you can find the distance by focusing on the y-coordinates.
Suppose you are looking for all the points on the x-axis that are exactly 3 units from the point (5, 0). You’re looking for points on the x-axis, so you know the points will have a y-coordinate of 0. Let the points you’re looking for be represented by (x, 0). The distance between (5, 0) and (x, 0) is 3, but you don’t know if (x, 0) is to the right of (5, 0) or to the left. You can write an absolute value equation about the x-coordinates.
|5 − x| = 3
Solving that equation will give you two x-coordinates.
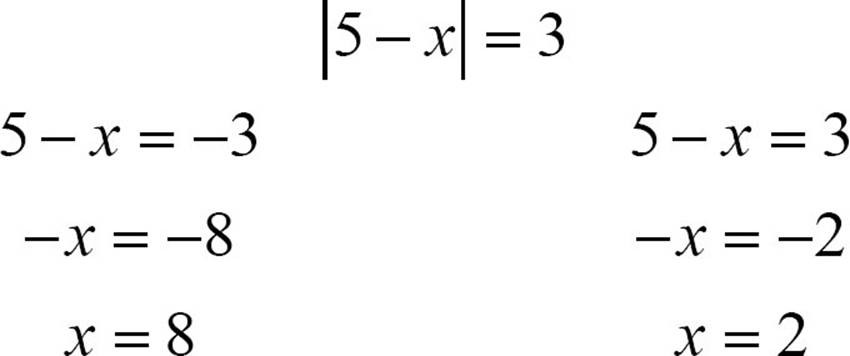
Each of these x-coordinates gives you a point that is 3 units from (5, 0). The points are (8, 0), three units to the right of (5, 0), and (2, 0), three units to the left of (5, 0).
![]()
CHECK POINT
Use an absolute value equation or inequality to solve each problem.
31. The difference between a number x and 14 is 22. Find all possible values for the number.
32. A number y is 24 units away from -17. Find all possible values of y.
33. If n represents all integers within 3 units of 9, find all possible values of n.
34. The difference between Peter’s salary and Paul’s is less than $4,000 a year. If Peter earns $82,500 per year, describe the possibilities for Paul’s salary.
35. Find all the points on the y-axis that are exactly 6 units from the point (0, -4).
36. Find all the points on the x-axis that are exactly 13 units from the point (-12, 0).
37. Find all the points on the y-axis that are exactly 10 units from the point (0, 3).
38. A body temperature that differs from the average of 98.6°F by more than 2° requires medical attention. What temperatures should receive medical attention?
39. The electricity supplied to most homes in the United States is designed to be 115 volts, but fluctuation within certain ranges is normal and natural. Too great a deviation can cause problems, however. Problems arise when the difference between the actual voltage V and the desired 115 volts exceeds 5 volts. Find the range of acceptable voltages.
40. Polling is used to predict the results of elections based on the responses of a relatively small group of respondents. In addition to giving the results of the poll, they often give a margin of error, which tells how far above or below their result they expect the actual result might be. If a candidate is predicted to earn 46% of the vote with a margin of error of 4%, in what range would you expect the candidate’s actual vote total to fall?
Linear equations and linear inequalities describe most of the situations you’ll encounter when solving problems, so being able to graph them efficiently is an important skill. If other, unusual relationships arise, we can always rely on the fundamental table of values to graph a new type of equation or inequality.
You know that absolute value equations in one variable can be translated into two linear equations and solved in ways very similar to solving linear equations. Absolute value inequalities translate into compound linear inequalities, so much of the work there is similar. It’s not surprising, therefore, that graphs of absolute value functions and absolute value inequalities are produced by methods similar to linear equations and inequalities.
Graphing Absolute Value Equations
Just as solving an absolute value equation involved solving two linear equations, graphing an absolute value equation turns out to mean graphing two linear equations, or at least parts of each of two linear equations. Let’s take a first look by means of a table of values.
![]()
TIP
The graph of an absolute value function is a V-shaped graph made up of two rays that meet at their endpoints. Remember that lines go on forever in both directions. Rays have one endpoint and continue endlessly in one direction. The sides of the V are rays with the same endpoint, which are called the vertex.
To graph y = |x|, first you need to choose values for x, including both positive and negative values, and evaluate for y.

Plot the points and connect them, but be careful. Don’t make assumptions about what the graph should look like. Let the points lead you. Here’s what it looks like after plotting the points.
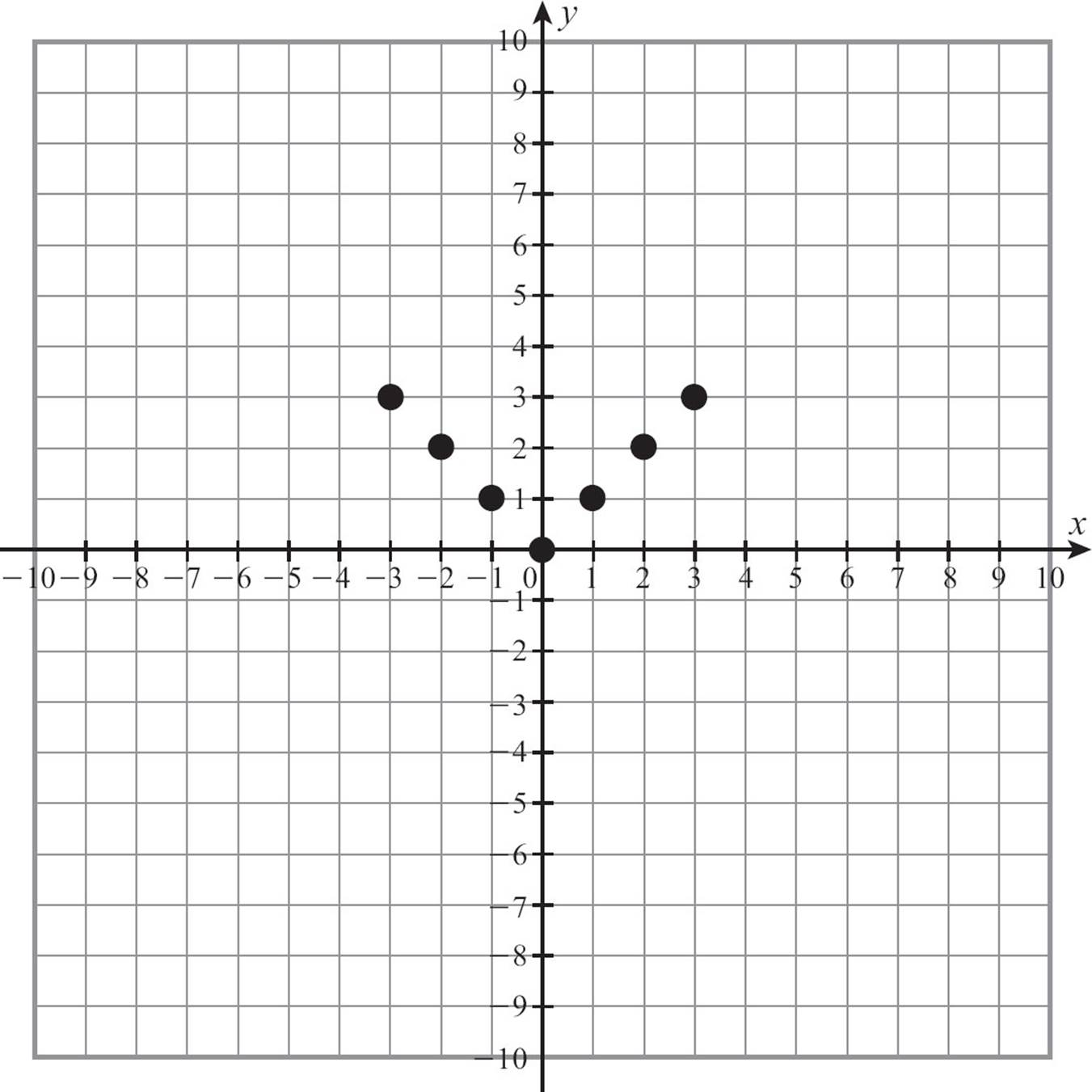
Can you see the two rays? The first few points from the table suggest a falling line, a line with a negative slope, and the last few create a rising line, with a positive slope, but you only want part of each one. You don’t want any points with negative y-coordinates. The two rays both have a y-intercept of 0, so they will intersect there at (0, 0). That meeting point is called the vertex.
![]()
DEFINITION
The vertex of an absolute value graph is the point where the two rays meet to form the point of the V-shape.
Don’t just grab a straight edge and draw lines from edge to edge of the grid, though. Remember that absolute value is never negative. The graph of y = |x| will never have any points with negative y-coordinates. So connect those falling points, and extend that ray upward, but don’t extend it beyond the origin. If you do, you’ll be going into negative y-values, and you don’t want that. In the same way, the rising portion of the graph can’t go below the x-axis. Here’s what the graph of y = |x| looks like.
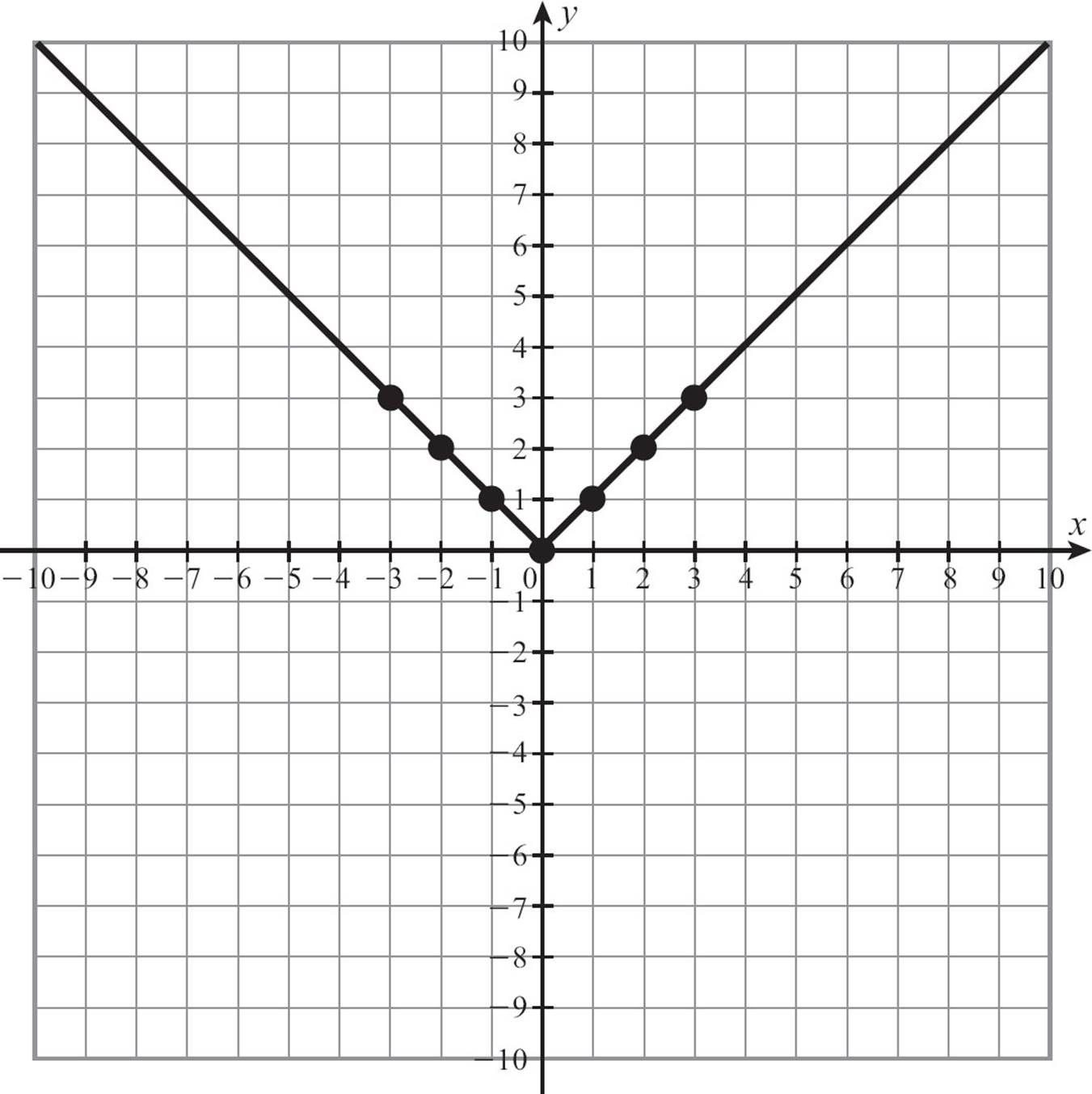
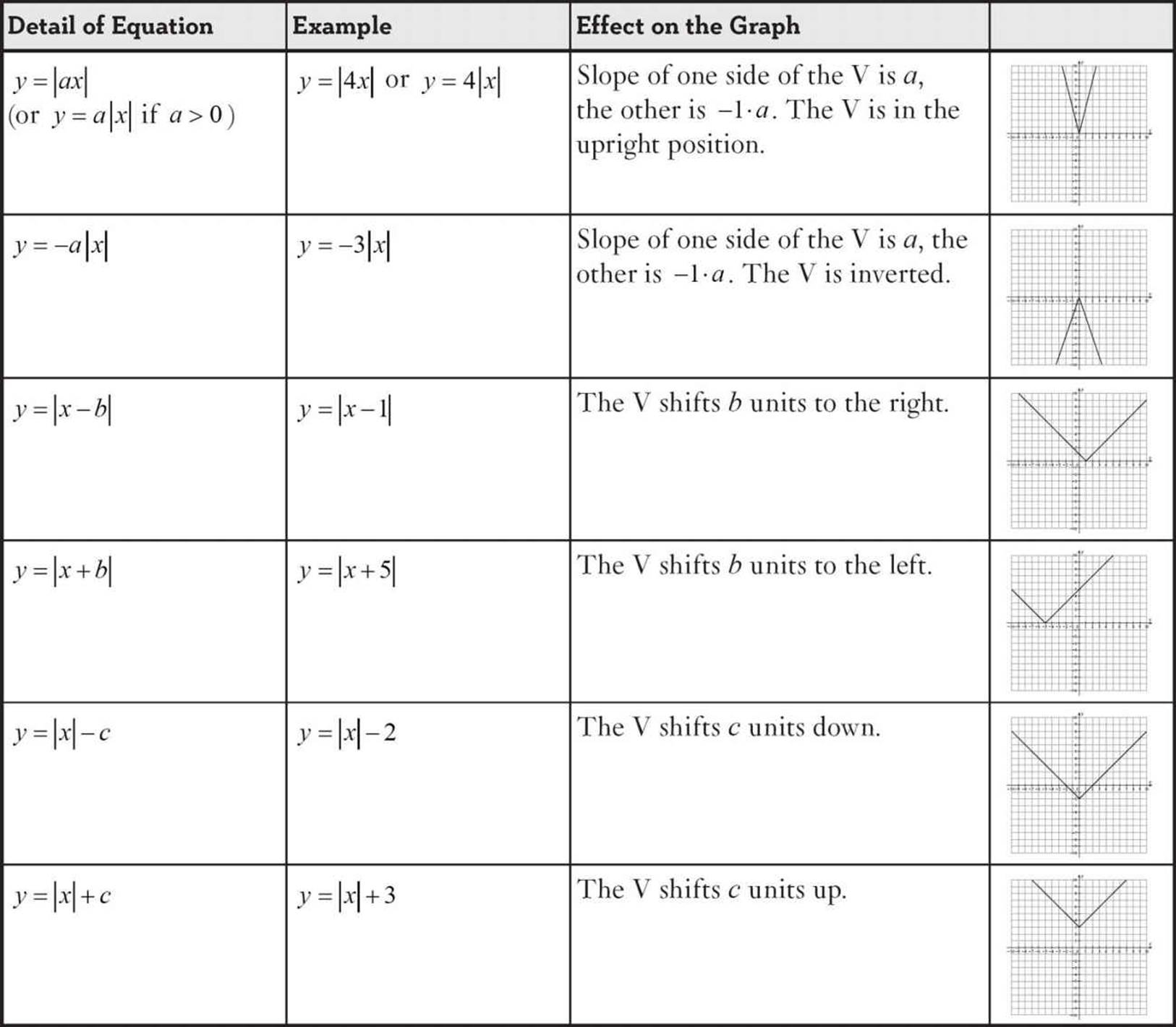
The V shape you see is characteristic of the graph of the absolute value function. Changes to the function’s rule may move the V left or right, up or down. The V may be narrow or wide, upright or upside down, but if it’s an absolute value function, its graph will have a V shape.
![]()
THINK ABOUT IT
Extending the sides of the absolute value graph in both directions will not only include points you don’t really want to include, but will also create a graph that is not a function. The absolute value function assigns to each input only one output: the magnitude of the number without its sign. If you extend the sides through the vertex, you’ll be including a second point for each x-coordinate, forming an X-shape that fails the vertical line test.
Any time you face a new type of function, you can always return to a table of values to produce the graph, but of course, it’s nice to use a quicker method if you can. The two sides of the V in the graph of the absolute value function are portions of the line y = x and y = −x. You know how to graph both of those quickly, so if you had a way to look at an absolute value function and predict what the two lines should be, graphing would be simple.
To find the basic shortcut, you can use what you know about solving absolute value equations. Suppose you wanted to solve |2x − 7| = 3. You would write two linear equations and solve each one.
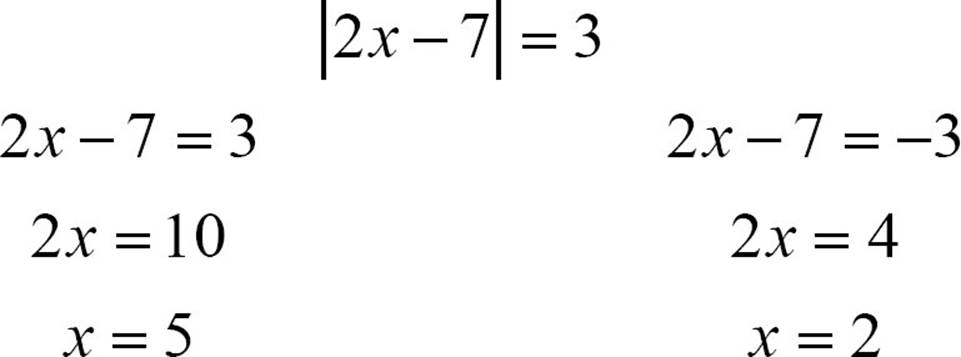
Now think about an absolute value function like y = |2x − 7|. If you rewrite that as |2x − 7| = y, you can see that the y is in the place of the 3 in the solution example. So let’s start thinking about the function to graph in the same way as the equation to be solved. Translate it into two equations.
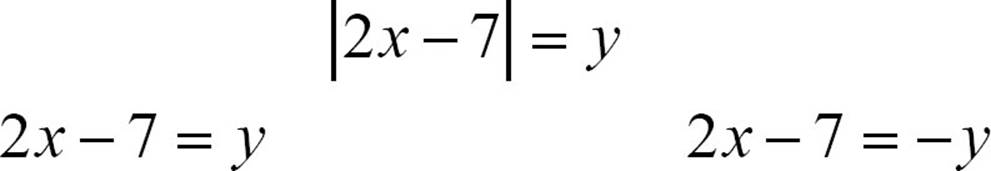
One of those equations is just y = 2x − 7, but the other needs a bit of cleaning up. You don’t want to know what –y equals. You want to know what y equals, so you need to multiply both sides by -1.
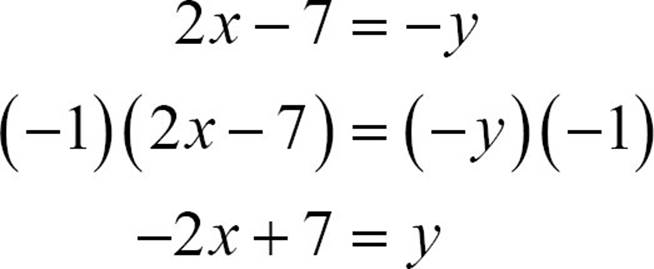
One side of the V-shaped graph is part of the line y = 2x − 7 and the other side is part of the line y = −2x + 7.
If you need to graph an absolute value function of the form y = |mx + b|, graph y = mx + b and y = −1(mx + b). Do not extend either one below the x-axis. The two lines should meet at the x-axis.
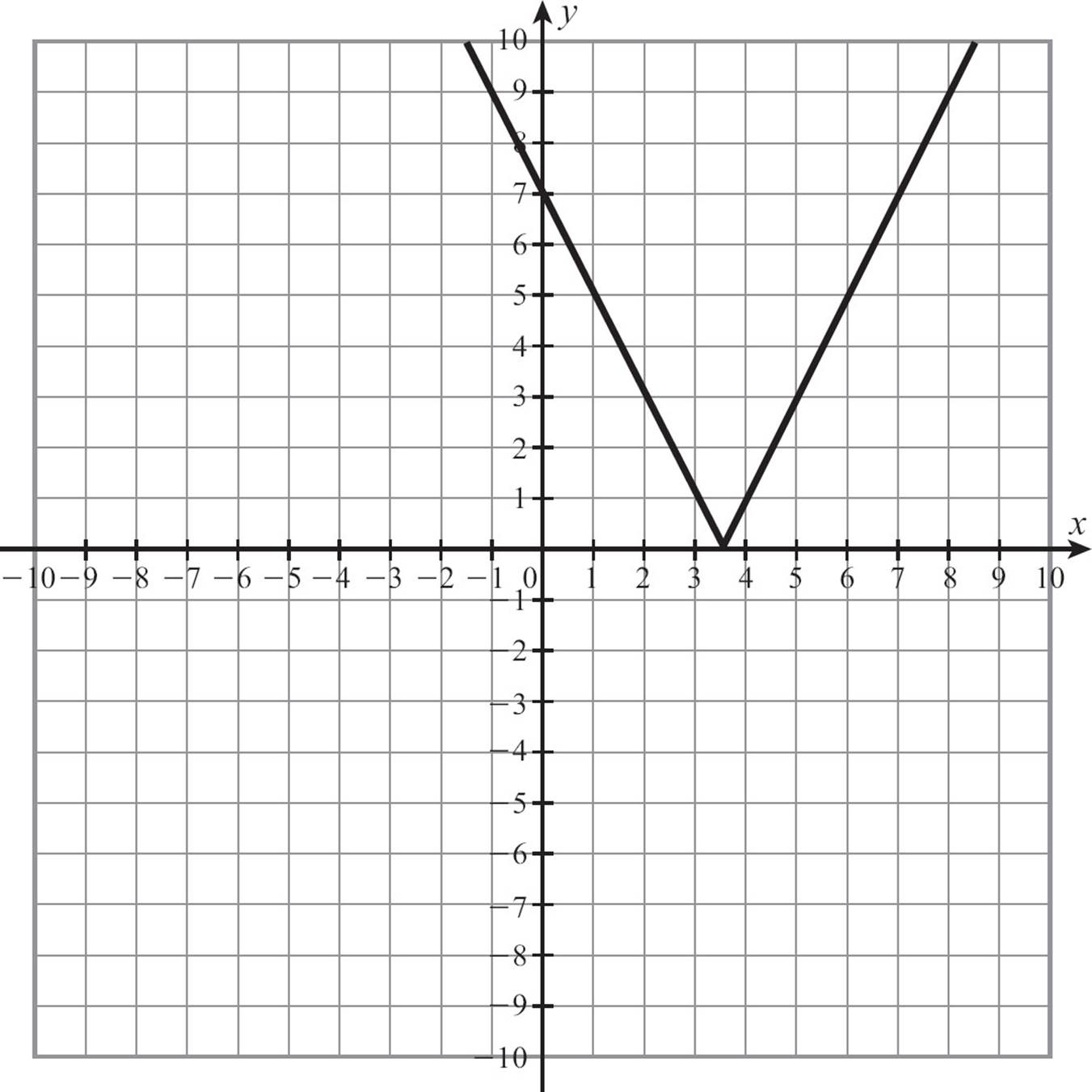
That’s a basic shortcut, but there is a complication. What if some operations are outside the absolute value signs? How do you graph y = |2x| − 7, if part of the expression, the 2x, is inside the absolute value sign and the –7 is outside? You don’t need to start all over. You just need to be clever. First add 7 to both sides, so that the absolute value is on one side and everything that’s not in the absolute value is on the other side.
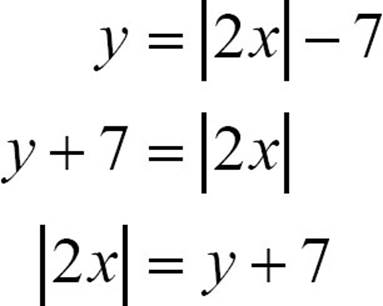
Now you can tackle it the way you dealt with solving absolute value equations. Rewrite it as two linear equations.
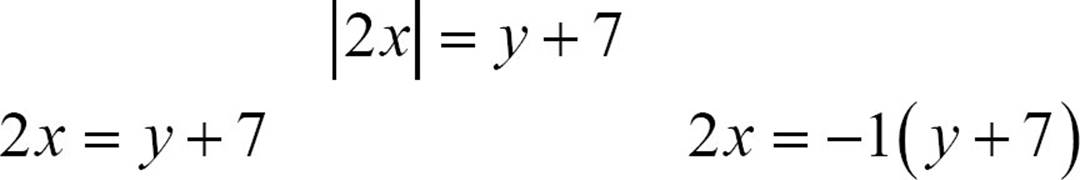
The first of those quickly simplifies to y = 2x − 7. The second takes a little work.
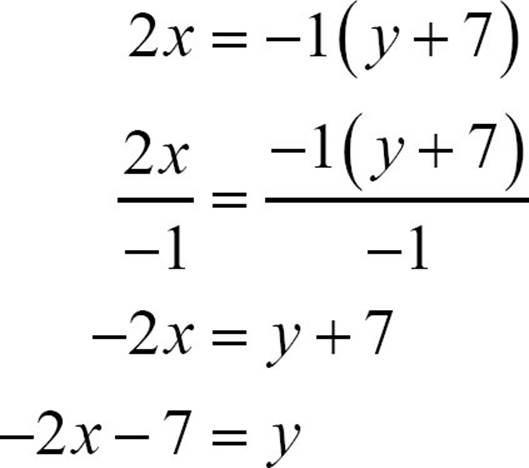
The second equation simplifies to y = −2x −7, and the first to y = 2x − 7. You have the positive and the negative version of the expression in the absolute value signs, but the constant term is unchanged. Your graph looks like this.
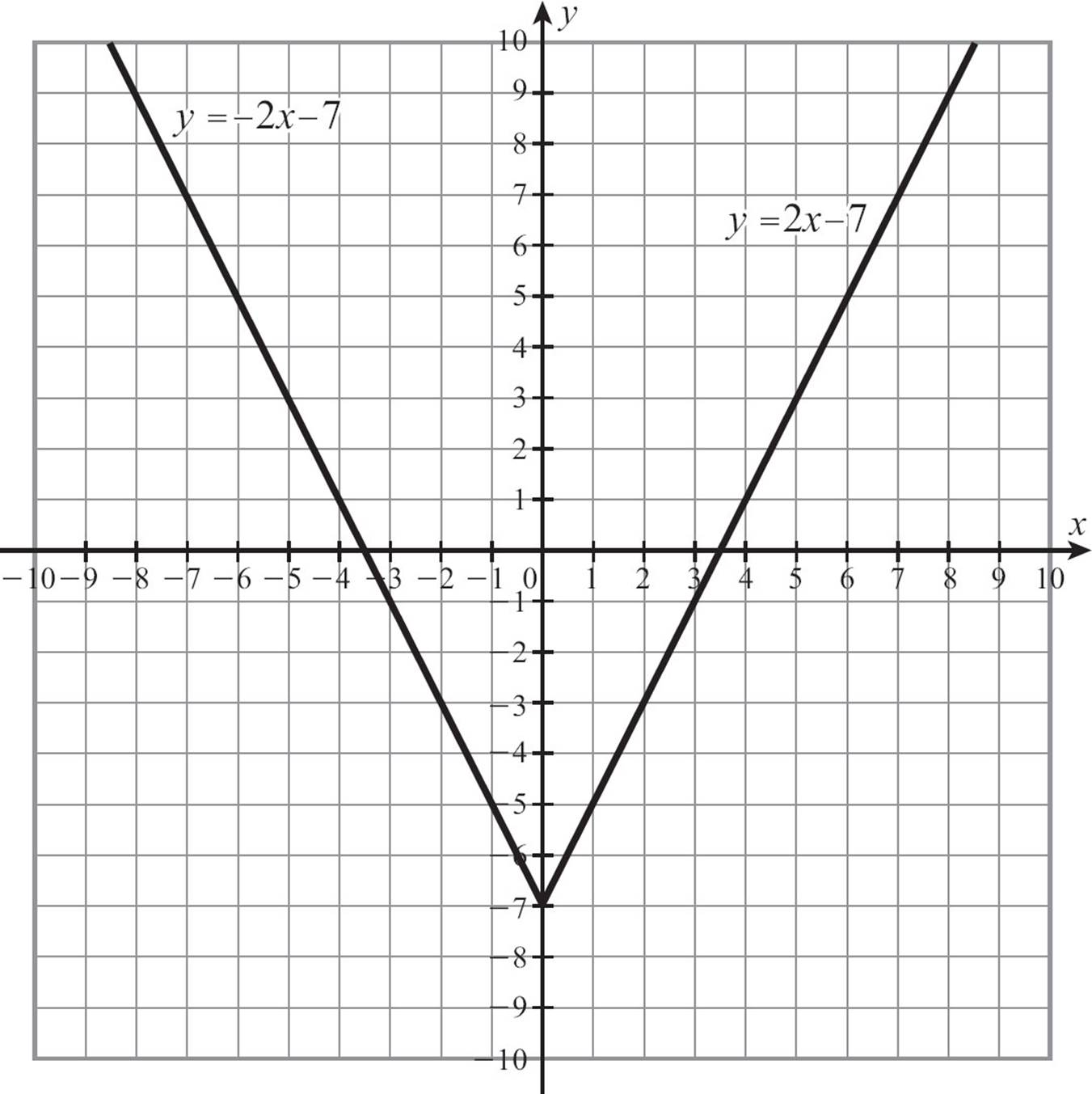
You can create a variant of our shortcut. To graph an absolute value function of the form y = |mx| + b, graph y = mx + b and y = −mx + b, to form the V shape.
Do you notice that the graph goes below the x-axis, into territory where the y-coordinates are negative? If the entire expression 2x − 7 were inside the absolute value signs, that shouldn’t happen, but because the equation y = |2x| − 7 tells you to subtract 7 after finding the absolute value, it is possible to produce negative y-values. Notice how far down the y-intercept is? It’s at -7. The absolute value part of the function would have values greater than or equal to zero, but that subtraction afterward pulls the graph down 7 units.
There are a few things you can say about the graph of an absolute value equation just by looking at the equation.
What an Equation Can Tell You About a Graph
![]()
CHECK POINT
Graph each absolute value equation.
41. y = |x − 3|
42. y = |x| + 1
43. y = |x + 1|
44. y = |x| − 5
45. y = |2x|
46. y = −3|x|
47. y = |2x − 5|
48. y = |7 − 4x|
49. y = |3x − 8|
50. y = |12 − 5x|
The Least You Need to Know
· Absolute value equations have two solutions, because the expression in the absolute value could be positive or negative.
· Absolute value inequalities translate to compound inequalities. Absolute value greater than a constant becomes an or inequality, and absolute value less than a constant becomes an and inequality.
· Absolute value equations and inequalities are useful in situations where more than one answer is possible.