Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 5. Advanced Topics in Differentiation
HANDS-ON ACTIVITY 5.1: LINEAR APPROXIMATIONS
Derivatives do so much. They report slopes of tangent lines, describe instantaneous velocities, and illustrate rates of change. Tangent lines, based so closely on derivatives, serve many similar purposes, but one of their most important characteristics is that tangent lines tend to act like the functions they’re tangent to, at least around the point of tangency.
NOTE. Linear approximations are the first step in a more complicated process known as Euler’s Method. Whereas approximations are on both the AB and BC tests, Euler’s Method appears only on the BC exam.
1. Give the equation of the tangent line to ![]() at x = 3.
at x = 3.
________________________________________________
________________________________________________
2. Graph f(x) and its tangent line on your calculator; draw the result below.
3. Zoom in three times on the point of tangency (using Zoom→Zoom in on the TI-83). What relationship do you notice between the two graphs at this level of magnification?
________________________________________________
________________________________________________
4. Return your graph to the standard viewing window (Zoom→standard). Calculate the value of both functions at x = 3.1 and x = 6. What conclusions can you draw?
________________________________________________
________________________________________________
________________________________________________
5. Describe the special property of tangent lines that is made clear in this activity; make sure to note any drawbacks or weaknesses inherent in this method.
________________________________________________
________________________________________________
6. Use a tangent line (linear approximation) to estimate the value of f(5.12) if f(x) = ![]()
________________________________________________
________________________________________________
________________________________________________
SOLUTIONS TO HANDS-ON ACTIVITY 5.1
1. The tangent line has equation 3x - 4y = -8.
2.
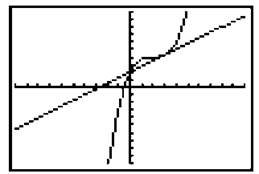
NOTE. The tendency of a graph to look and act like its tangent line immediately surrounding the point of tangency is called local linearity. Literally, the graph looks like a line in that localized area, as demonstrated by the zooming exercise in problem 3.
3. Various stages of zooming are shown here:

The two graphs have very similar values the closer you zoom in to the point of tangency. In fact, if you keep zooming in, it’s hard to tell the two graphs apart.
4. If you call the tangent line g(x),f(3.1) = 4.33275 and g(3.1) = 4.325. These values are extremely close. However, f(6) = 20 and g(6) = 6.5. These values aren’t even in the same ballpark. The clear conclusion: the tangent line only approximates the function’s values near the point of tangency. Further away from this point, all bets are off.
5. I drew this conclusion in number 4; clearly, I am an overachiever.
6. First, find the equation of the tangent line to f at x = 5; because 5.12 is close to 5, the function and the tangent line at x = 5 will have similar values.
f'(x) = 6x + 21x-4
f'(5) = 30.0336
The tangent line—which passes through (5,74.944)—has slope 30.0336. Thus, tangent line has the following equation:
y - 74.944 = 30.0336(x - 5)
Now, evaluate the tangent line for x = 5.12 for your approximation, and you get 78.548.
EXERCISE 2
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE YOUR CALCULATOR FOR ALL OF THESE PROBLEMS
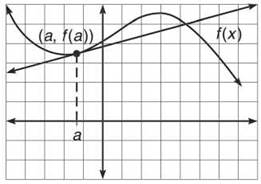
1. In the diagram below, the function f(x) meets its tangent line at the point (a/(a)). What is the equation of the linear approximation to f at x = a?
2. Use a linear approximation centered at 2 to estimate j(2.14) if ![]()
3. If h(0) = 4 and h'(0) = -5, use a linear approximation to estimate h(.25).
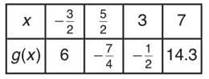
4. If g(x) is a continuous and differentiable function and contains the values given by the table below, estimate g(3.2) with a linear approximation.
ANSWERS AND EXPLANATIONS
1. The equation of the linear approximation is simply the equation of the tangent line through the point (a,f(a)) with slope f'(a): y — f(a) = f'(a)(x — a).
2. The linear approximation is given by the equation of the tangent line to j at (2,18.52258872). So, find the slope of the tangent line by calculating the numerical derivative.
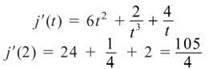
The equation of the tangent line (linear approximator) is
![]()
Substitute x = 2.14 to get an approximation of 22.198 for j(2.14).
3. Begin by finding the equation of the tangent line to h when x = 0 (since .25 is close to 0, and all the information we have centers around 0). You already know the slope of the line will be —5 and the point of tangency is (0,4), so the equation of the line is y = —5x + 4. The linear approximation for x = .25 is given by —5(.25) + 4 = 2.75.
4. The best approximation for g(3.2) will be given by the tangent line constructed at x = 3. Clearly, the point of tangency is (3,—1/2), but you’ll have to approximate the derivative at x = 3 using the secant line connecting (5/2,—7/4) and (3,—1/2). That secant slope ∆y/∆x is 5/2. Therefore, the best linear approximation you can make is
![]()
Evaluate this equation for x = 3.2, and your approximation is 0.