Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 5. Advanced Topics in Differentiation

L’HOPITAL’S RULE (BC TOPIC ONLY)

L’Hopital’s Rule may sound like the tyrannical rule of a French monarch, but it is actually a way to calculate indeterminate limits. What is an indeterminate limit, you ask? There are numerous forms that an indeterminate limit can take, but you should concentrate on indeterminate forms 0/0, 0 ∙ ∞, and ∞/∞. Until now, you were unable to evaluate limits that ended with those results, but now, you will face no such restrictions. Although L’Hopital’s Rule is a BC topic, it is perhaps one of the easiest things in calculus to apply and understand, and AP students are well served to learn it also.

To explore L’Hopital’s Rule, we will revisit an example from the Special Limits section of Chapter 3: Substitution resulted in 0/0, which is indeterminate. None of our other techniques (e.g., factoring, conjugate) applied to this problem either, so we used the graph of sin x/x to find the limit of 1. If you don’t have access to a graphing calculator, however, this problem is a lot more difficult, as the graph is far from trivial to draw. Enter L’Hopital’s Rule.

L’Hopital’s Rule: If f(x) = g(x) = 0 or f(x) = g(x) = ∞, then

Translation: If you are trying to evaluate a limit and you end up with 0/0 or ∞/∞, you can take the derivatives of the numerator and denominator separately. The new fraction will have the same limit as the original problem, so try and evaluate it. If you get another indeterminate answer, you can repeat the process.

Example 3: Use L’Hopital’s Rule to evaluate

Solution: As stated previously, substitution results in 0/0. Apply L’Hopital’s Rule by deriving sin x and x (with respect to x):

Note that sin x/x and cos x/1 are not equal, but they will have the same limit as x approaches 0. The new problem, is very easy by substitution. Thanks to the unit circle, you know cos 0 = 1, which is the answer you memorized “back in the day.”

TIP. L’Hopital’s Rule is for use only with indeterminate limits!

Example 4: Evaluate

Solution: Remember this one? It’s the other limit you memorized. Because substitution results in 0/0, apply L’Hopital’s Rule to get Evaluate the new limit by substitution, and you get 0/1, or 0. (Another answer you probably expected. If you didn’t expect it, it probably feels like Christmas.)

Example 5: Evaluate

Solution: If you substitute, you get ∞ ∙ 0, which is an indeterminate form, but you need a fraction to use L’Hopital and his fabulous rule. However, you can rewrite the expression as x/e^x. Substitution now results in ∞/∞, and it’s time to whip out L’Hopital; after differentiating, you get

Substitution results in 1/e^∞ or 1/∞, which is 0, according to our special limit rules from Chapter 3.

NOTE. There is no limit to how many times L’Hopital’s Rule can be applied in a problem, as long as each preceding limit is indeterminate.

Example 6: Evaluate using L’Hopital’s Rule.

Solution: You should be able to get the answer simply by looking at the problem—it’s a limit at infinity of a rational function. So, you should compare the degrees of the numerator and denominator. Because the degrees are equal, the limit is the quotient of the leading coefficients: —2/3. You can verify this with L’Hopital. (Substitution results in ∞/∞, so L’Hopital’s Rule is allowed.) First, find the derivatives as you have done:

Substitution still results in ∞/∞, so apply LHopital’s a second time.

EXERCISE 3

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

YOU MAY NOT USE YOUR GRAPHING CALCULATOR FOR THESE

Evaluate the following limits.

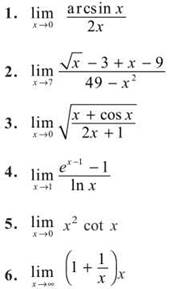(Hint: use natural log)

ANSWERS AND EXPLANATIONS

1. Substitution results in 0/0, so L’Hopital it to get

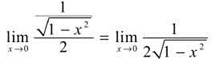
Now, substitution will work, and the answer is 1/2.

2. The substitution of x = 7 results in 0/0, souse L’Hopital’s Rule; you should get At this point, it is no longer illegal to substitute 7; in fact, doing so results in the following:

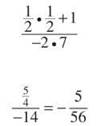
3. Were you fooled? L’Hopital’s Rule is not applicable to this problem, because substitution results in 1/1, so the limit is equal to 1. Remember to apply L’Hopital’s Rule only in cases of indeterminate limits.

4. Deja vu all over again! Indeterminate form 0/0 makes its encore appearance. L’Hopital is waiting in the wings to tackle this problem like Kevin Costner in The Bodyguard:

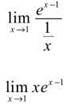
Substitution results in 1 ∙ 1 =1.

5. This limit is of indeterminate form 0 ∙ ∞. In order to apply L’Hopital’s Rule, you’ll need a fraction. Because tan x and cot x are reciprocals, you can rewrite the limit as Now, the indeterminate form 0/0 occurs, so you know what to do:

Substitution results in 0/1, which, of course, is 0.

NOTE. The indeterminate form exhibited by problem 6 is 1^∞; while 0/0 and ∞/∞ are, by far, the most common indeterminate forms on the AP test, there is a slight chance you may see this form or even 0⁰ a swell.

6. This one is a bit tricky, although you hopefully recognize it from the special limits section; the answer is supposed to be e. In order to find the answer, we make the crazy assumption that there is an answer, and we call it y:

Here’s where the hint comes in. Take the natural log of both sides of this equation:

You can pull that limit out of the natural log (don’t worry so much about why you can) and bring the x exponent down using log properties:

This limit is the indeterminate form ∞ ∙ 0, so you can apply L’Hopital’s Rule as soon as you make it a fraction. If you rewrite x as (which is not too obvious to most people), you get the indeterminate form 0/0, so apply L’Hopital’s Rule:

Finally, substitution is not illegal, and you can find the limit:

ln y = 1

However, your original goal was to find the limit expressed as y, so you’ll have to solve this equation for y by writing e to the power of both sides of the equation:

e^ln y = e¹

y = e

This is the answer we expected, although I don’t know that we expected the massive amount of work required.