5 Steps to a 5: AP Calculus AB 2017 (2016)
APPENDIX
1. Quadratic Formula:
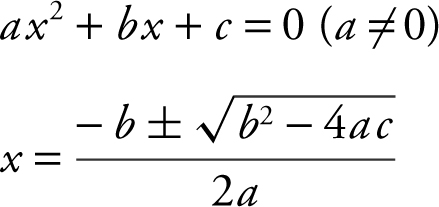
2. Distance Formula:
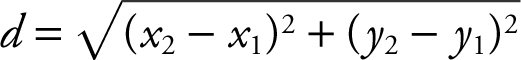
3. Equation of a Circle:
x 2 + y 2 = r 2 center at (0, 0) and radius = r .
4. Equation of an Ellipse:
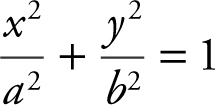center at (0, 0).
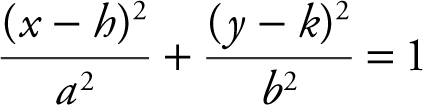center at (h , k ).
5. Area and Volume Formulas:
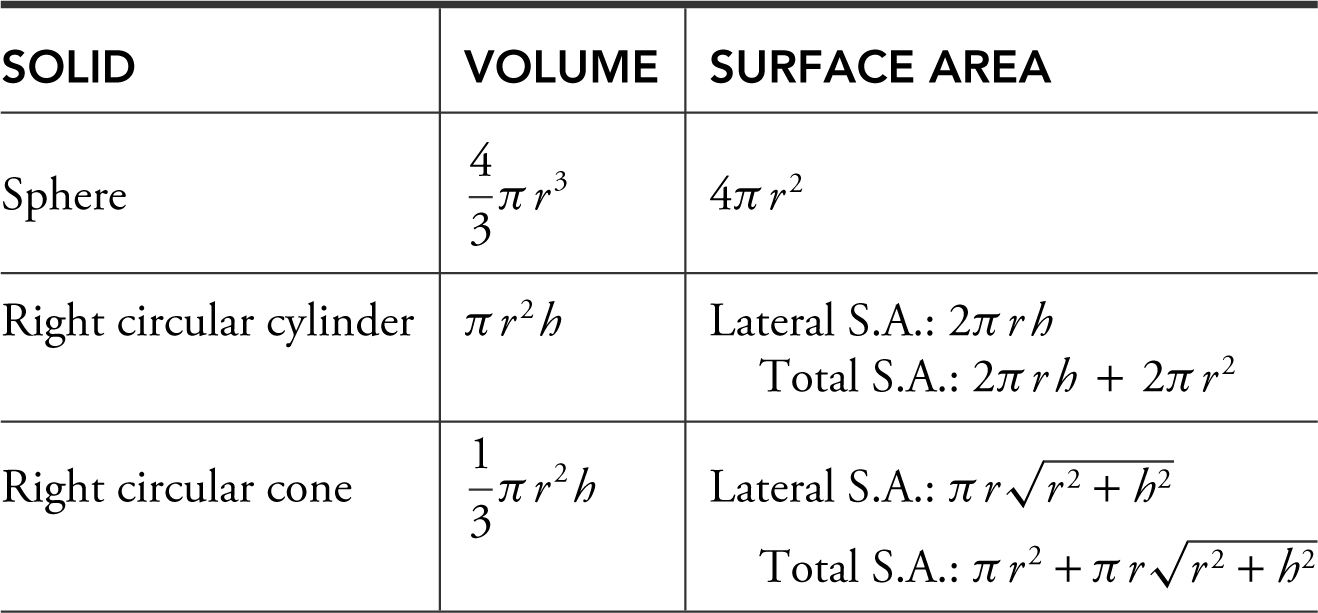
6. Special Angles:
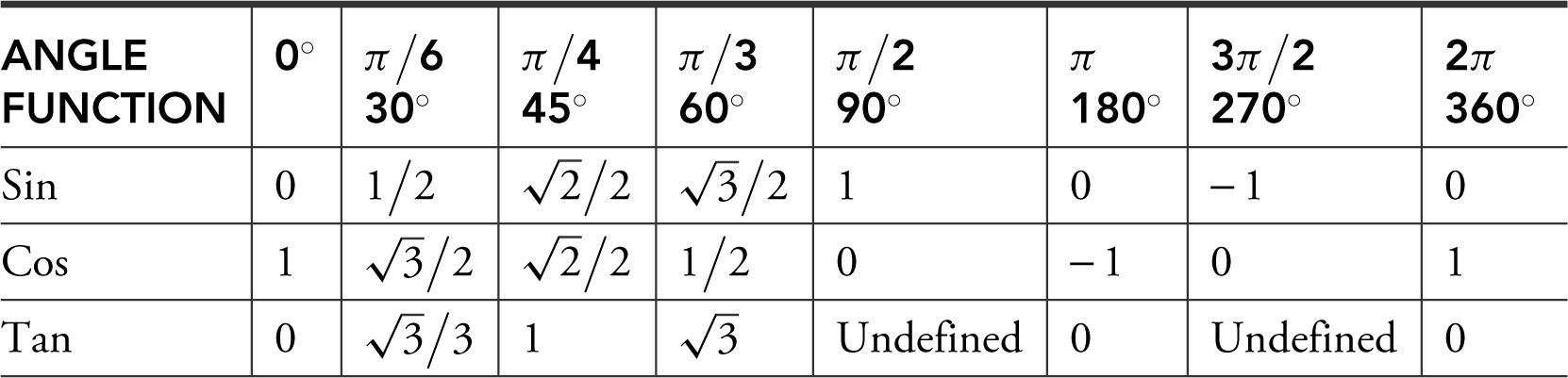
7. Double Angles:
• sin 2θ = 2 sin θ cos θ
• cos 2θ = cos2 θ – sin2 θ or 1 – 2 sin2 θ or 2 cos2 θ – 1.
• 
• 
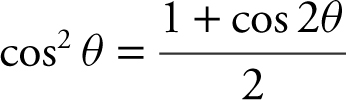
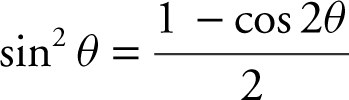
8. Pythagorean Identities:
• sin2 θ + cos2 θ = 1
• 1 + tan2 θ = sec2 θ
• 1 + cot2 θ = csc2 θ
9. Limits:
• 
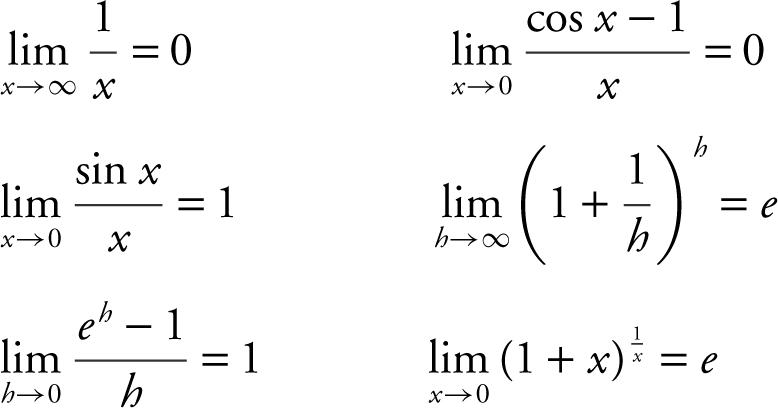
10. L’Hôpital’s Rule for Indeterminate Forms Let lim represent one of the limits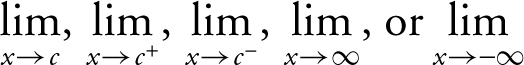 
. Suppose f (x ) and g (x ) are differentiable and g ′(x ) ≠ 0 near c , except possibly at c , and suppose lim f (x ) = 0 and lim g (x ) = 0. Then the lim 
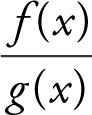is an indeterminate form of the type 
. Also, if lim f (x ) = ±∞ and lim g (x ) = +∞, then the lim 
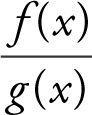is an indeterminate form of the type 
. In both cases, and 
, L’Hôpital’s Rule states that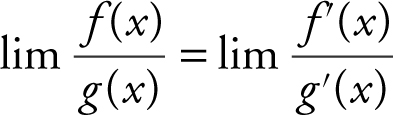 
.
11. Rules of Differentiation:
a. Definition of the Derivative of a Function:
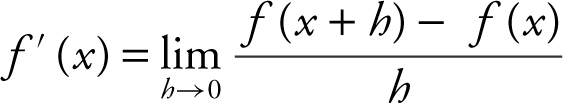
b. Power Rule: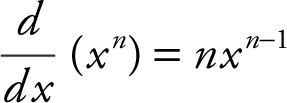 
c. Sum & Difference Rules:
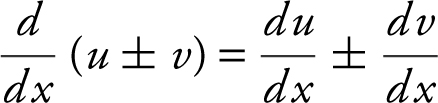
d. Product Rule:
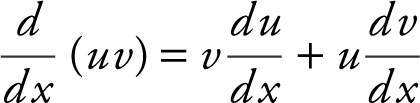
e. Quotient Rule:
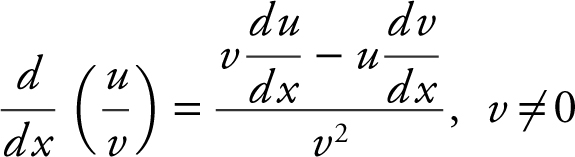
Summary of Sum, Difference, Product, and Quotient Rules:
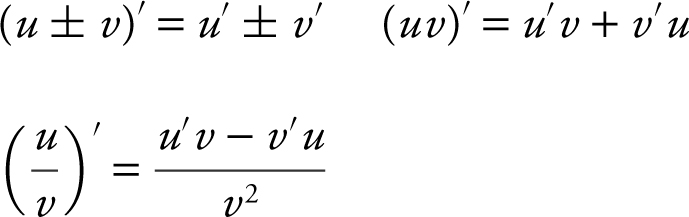
f. Chain Rule:
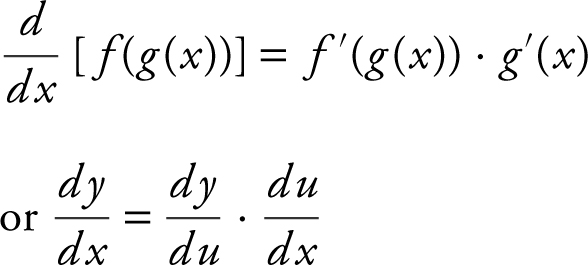
12. Inverse Function and Derivatives:
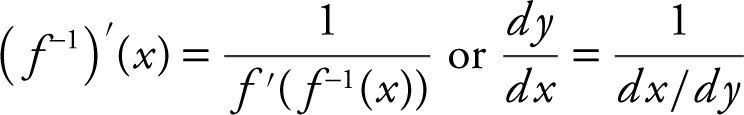
13. Differentiation and Integration Formulas: Integration Rules
a.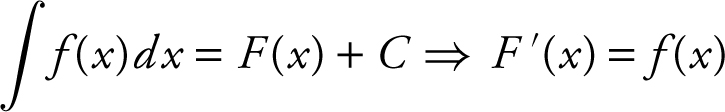 
b.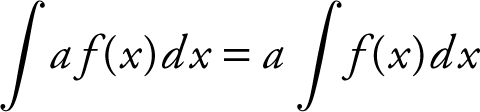 
c.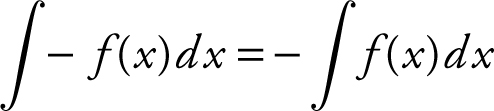 
d.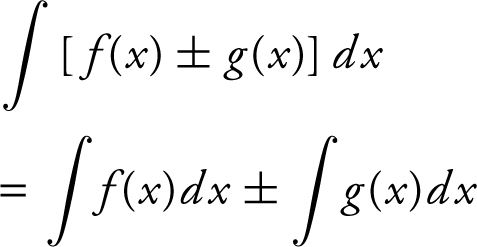 
Differentiation Formulas:
a.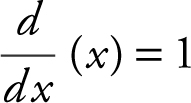 
b.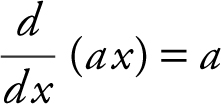 
c.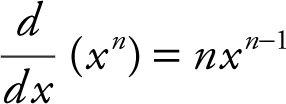 
d.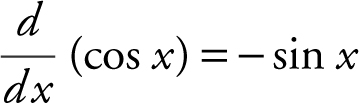 
e.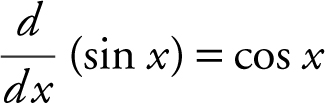 
f.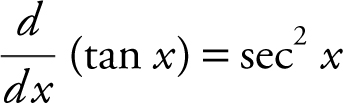 
g.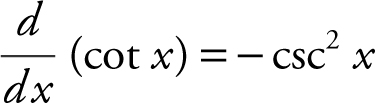 
h.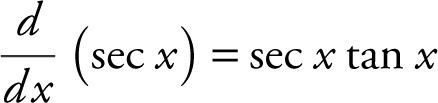 
i.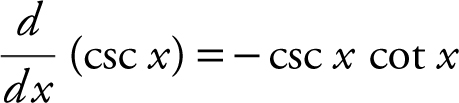 
j.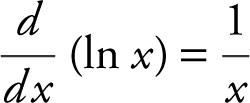 
k.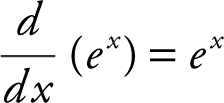 
l.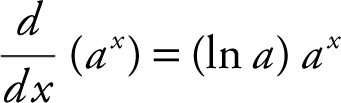 
m.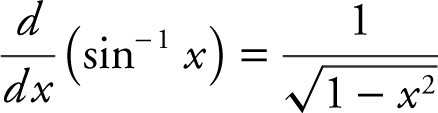 
n.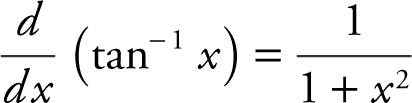 
o.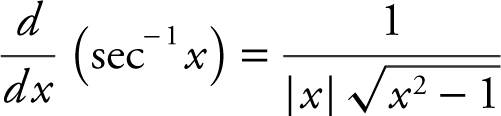 
Integration Formulas:
a.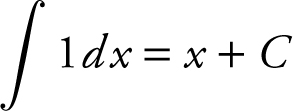 
b.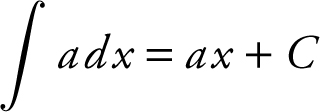 
c.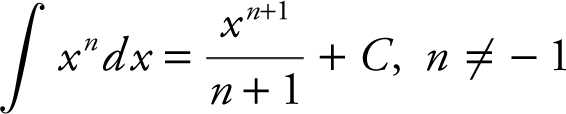 
d.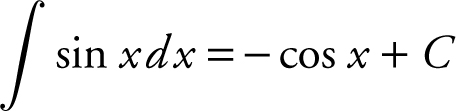 
e.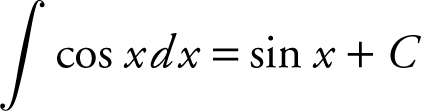 
f.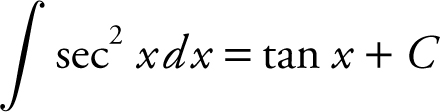 
g.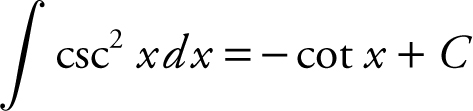 
h.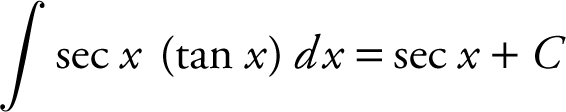 
i.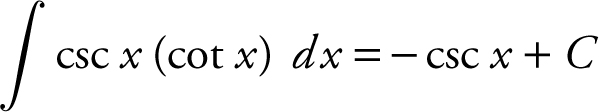 
j.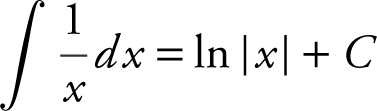 
k.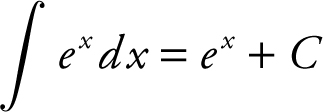 
l.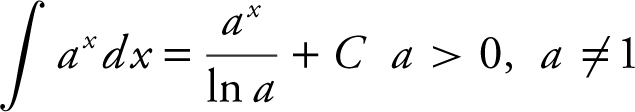 
m.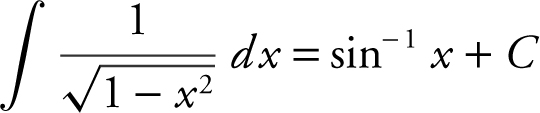 
n.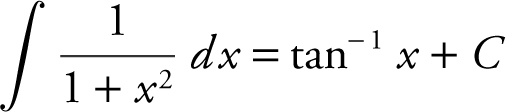 
o.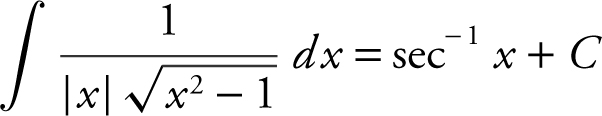 
More Integration Formulas:
a.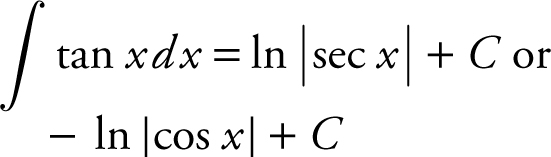 
b.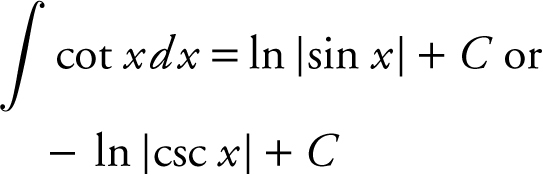 
c.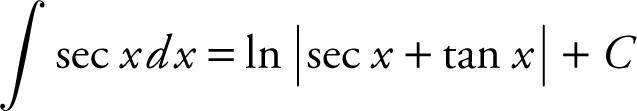 
d.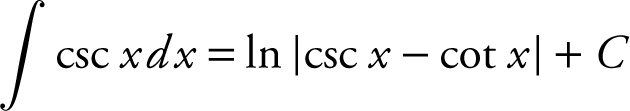 
e.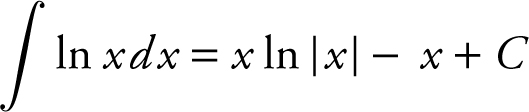 
f.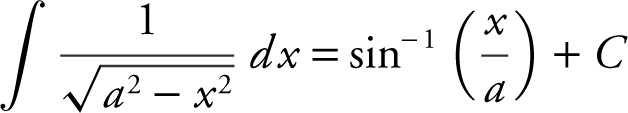 
g.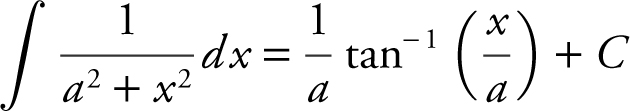 
h.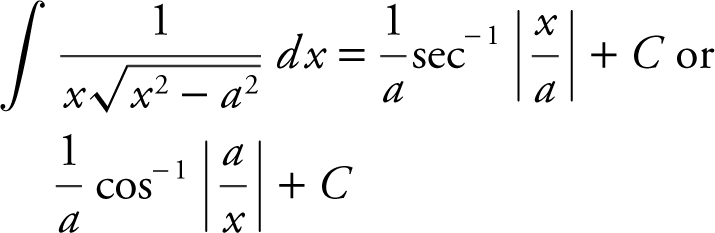 
i.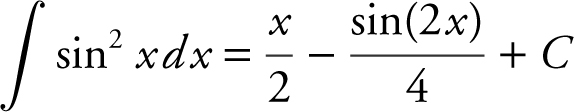 
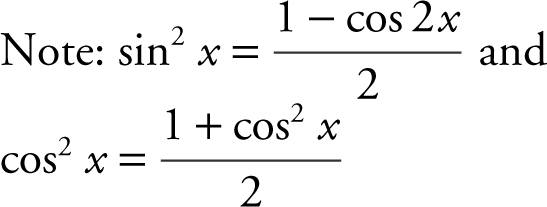
Note: After evaluating an integral, always check the result by taking the derivative of the answer (i.e., taking the derivative of the antiderivative).
14. Intergration by parts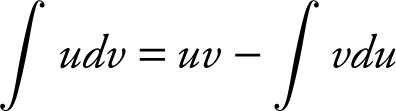 
(and follow LIPET Rule).
15. The Fundamental Theorem of Calculus
,
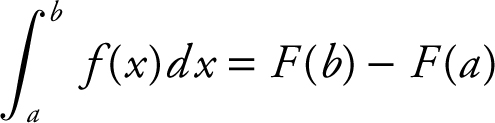where F ′(x ) = f (x ).
.
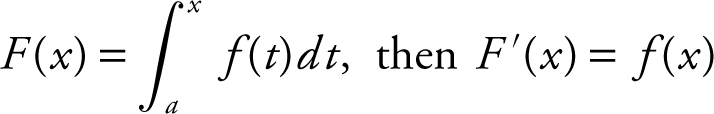16. Trapezoidal Approximation:
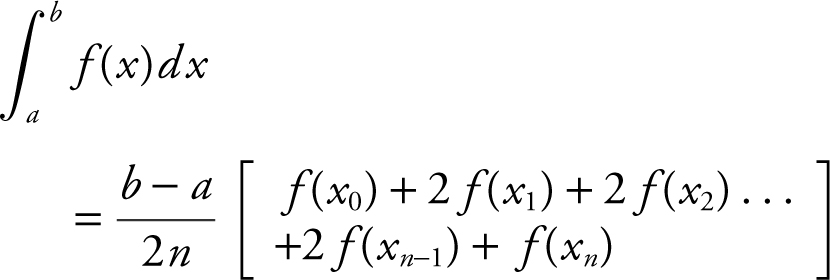
17. Average Value of a Function:
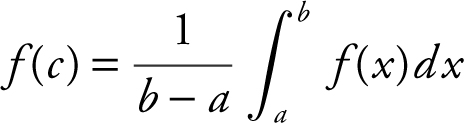
18. Mean Value Theorem:
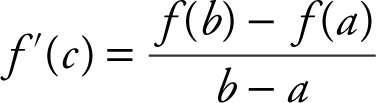for some c in (a , b ).
Mean Value Theorem for Integrals:
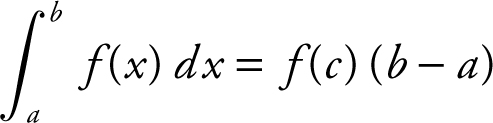for some c in (a , b ).
19. Area Bounded by 2 Curves:
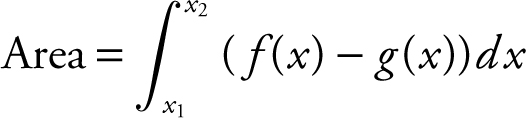
where f (x ) ≥ g (x ).
20. Volume of a Solid with Known Cross Section:
,
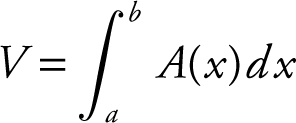where A (x ) is the cross section.
21. Disc Method:
.
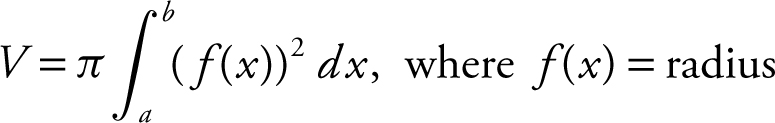22. Using the Washer Method:
,
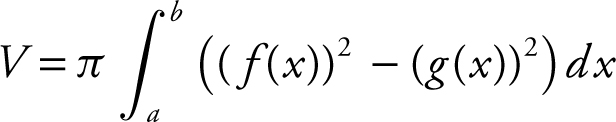where f (x ) = outer radius and g (x ) = inner radius.
23. Distance Traveled Formulas:
• Position Function: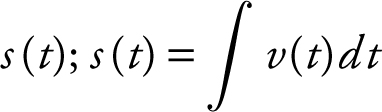 
• Velocity: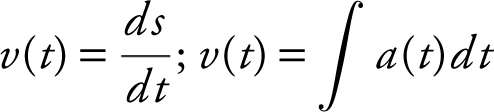 
• Acceleration: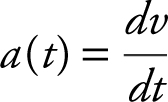 
• Speed: |v (t )|
• Displacement from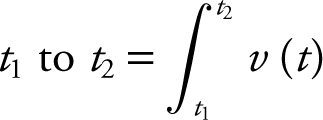 
= s (t 2 ) – s (t 1 ).
• Total Distance Traveled from t 1 to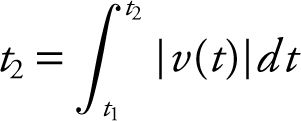 
.
24. Business Formulas:
.
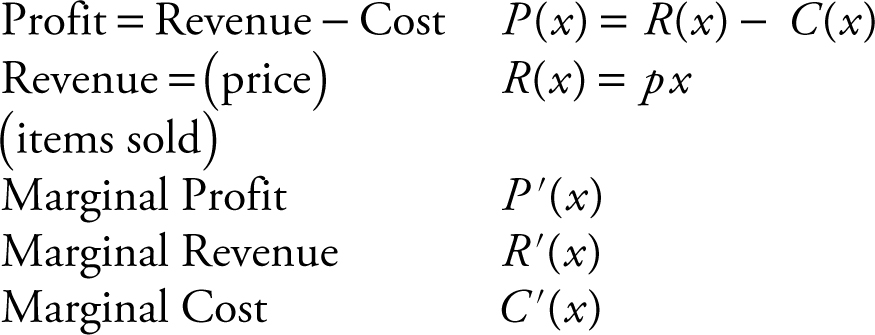P ′(x ), R ′(x ), C ′(x ) are the instantaneous rates of change of profit, revenue, and cost respectively.
25. Exponential Growth/Decay Formulas:
.
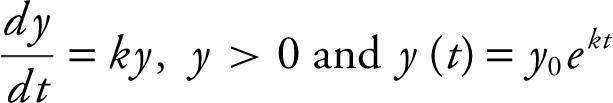APPENDIX
1. Quadratic Formula:
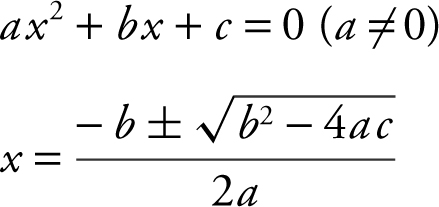
2. Distance Formula:
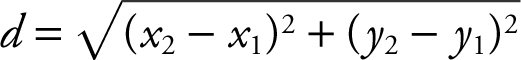
3. Equation of a Circle:
x 2 + y 2 = r 2 center at (0, 0) and radius = r .
4. Equation of an Ellipse:
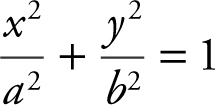center at (0, 0).
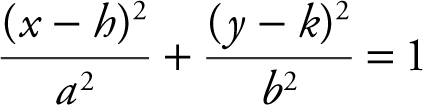center at (h , k ).
5. Area and Volume Formulas:
6. Special Angles:
7. Double Angles:
• sin 2θ = 2 sin θ cos θ
• cos 2θ = cos2 θ – sin2 θ or 1 – 2 sin2 θ or 2 cos2 θ – 1.
•
•
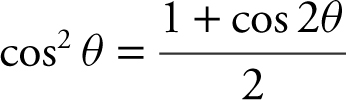
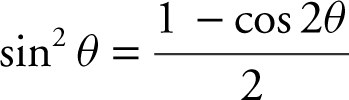
8. Pythagorean Identities:
• sin2 θ + cos2 θ = 1
• 1 + tan2 θ = sec2 θ
• 1 + cot2 θ = csc2 θ
9. Limits:
•
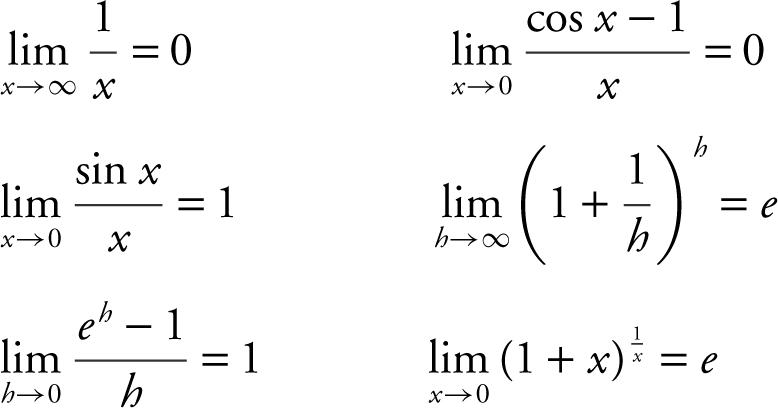
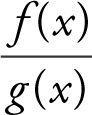10. L’Hôpital’s Rule for Indeterminate Forms Let lim represent one of the limits . Suppose f (x ) and g (x ) are differentiable and g ′(x ) ≠ 0 near c , except possibly at c , and suppose lim f (x ) = 0 and lim g (x ) = 0. Then the lim is an indeterminate form of the type . Also, if lim f (x ) = ±∞ and lim g (x ) = +∞, then the lim is an indeterminate form of the type . In both cases, and , L’Hôpital’s Rule states that .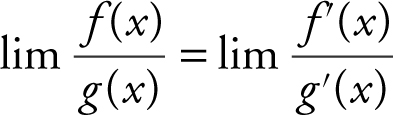
11. Rules of Differentiation:
a. Definition of the Derivative of a Function:
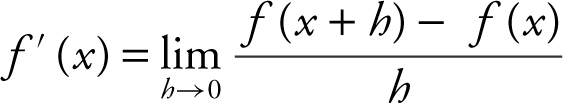
b. Power Rule: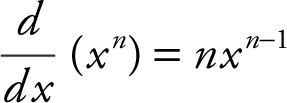
c. Sum & Difference Rules:
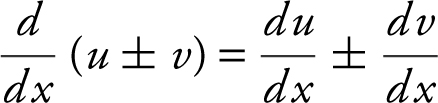
d. Product Rule:
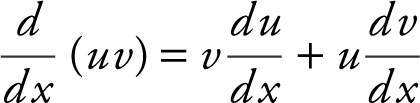
e. Quotient Rule:
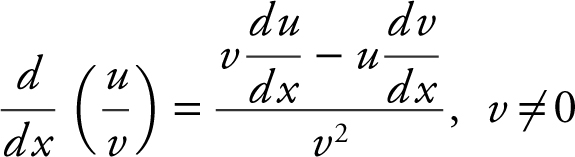
Summary of Sum, Difference, Product, and Quotient Rules:
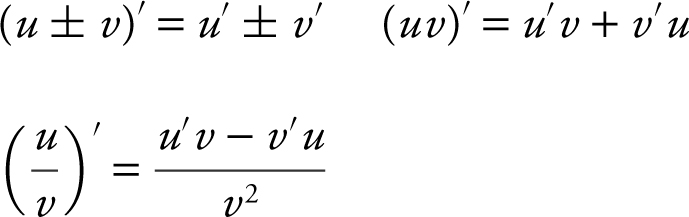
f. Chain Rule:
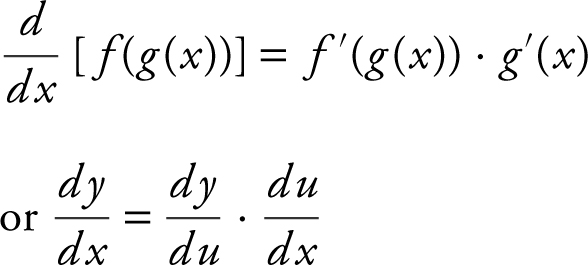
12. Inverse Function and Derivatives:
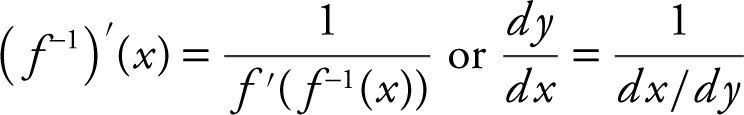
13. Differentiation and Integration Formulas: Integration Rules
a.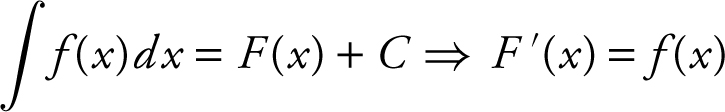
b.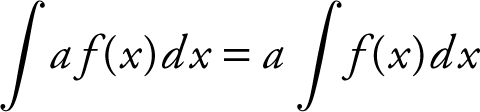
c.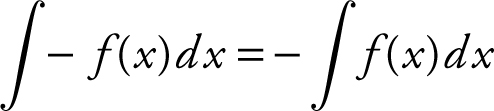
d.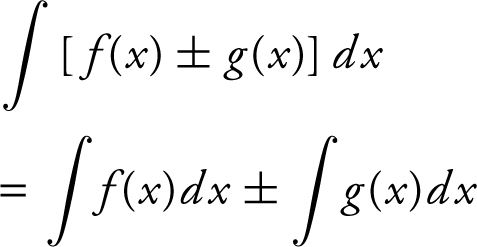
Differentiation Formulas:
a.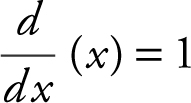
b.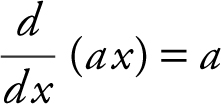
c.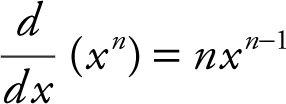
d.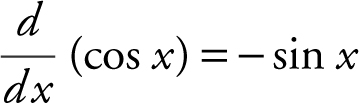
e.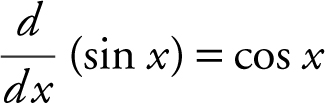
f.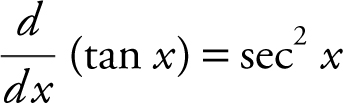
g.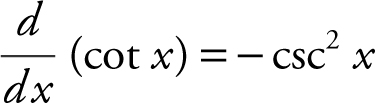
h.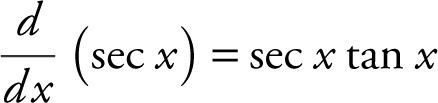
i.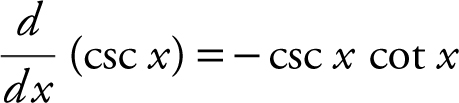
j.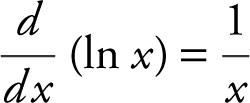
k.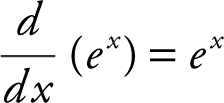
l.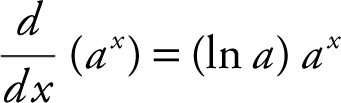
m.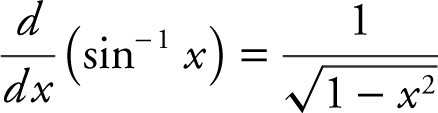
n.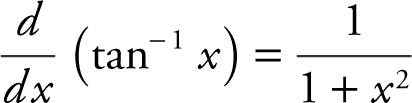
o.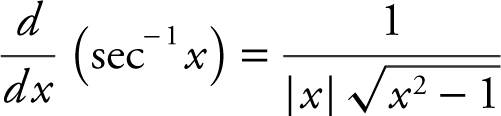
Integration Formulas:
a.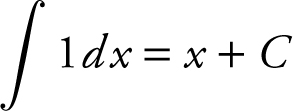
b.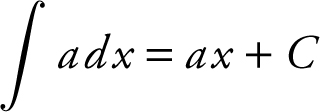
c.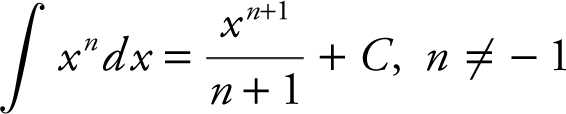
d.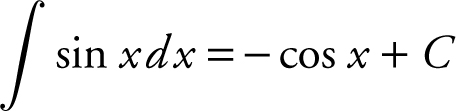
e.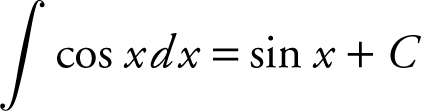
f.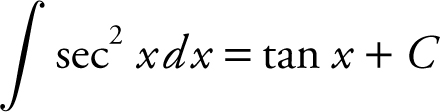
g.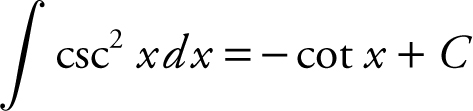
h.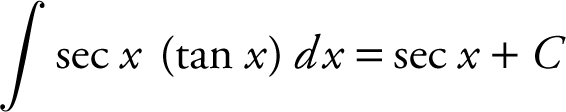
i.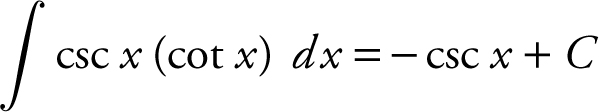
j.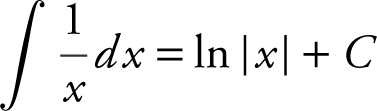
k.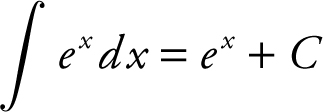
l.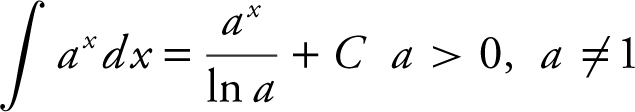
m.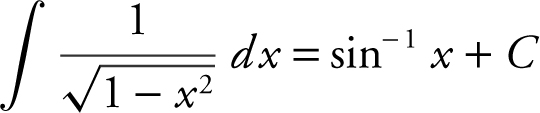
n.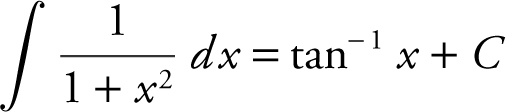
o.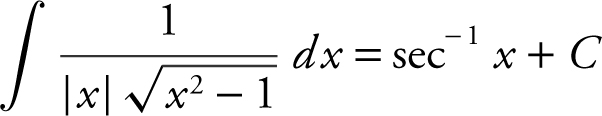
More Integration Formulas:
a.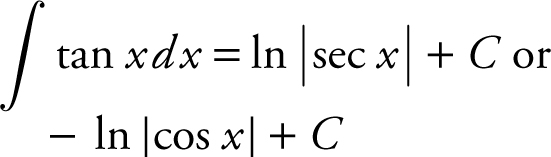
b.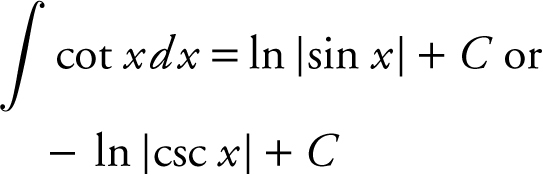
c.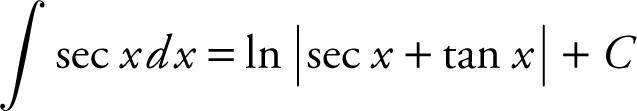
d.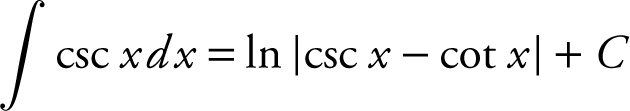
e.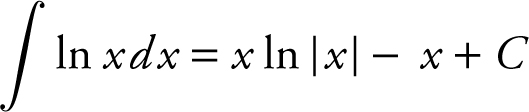
f.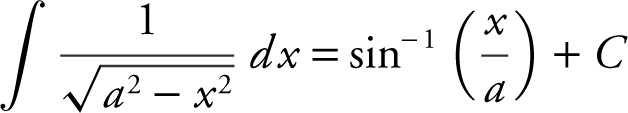
g.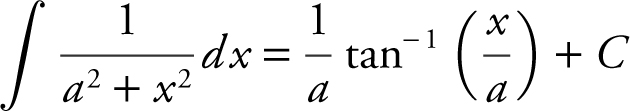
h.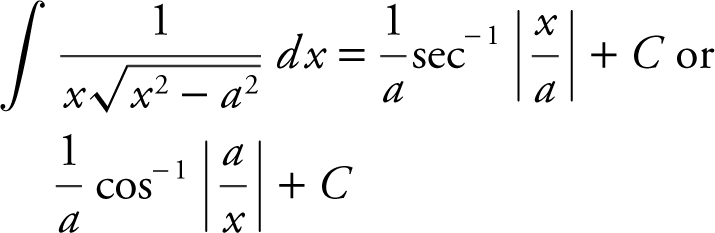
i.
Note: After evaluating an integral, always check the result by taking the derivative of the answer (i.e., taking the derivative of the antiderivative).
14. Intergration by parts (and follow LIPET Rule).
15. The Fundamental Theorem of Calculus
,
where F ′(x ) = f (x ).
.
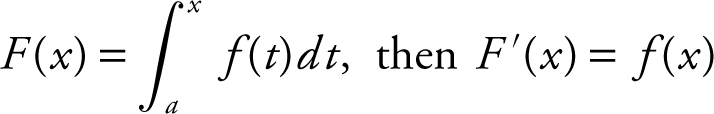16. Trapezoidal Approximation:
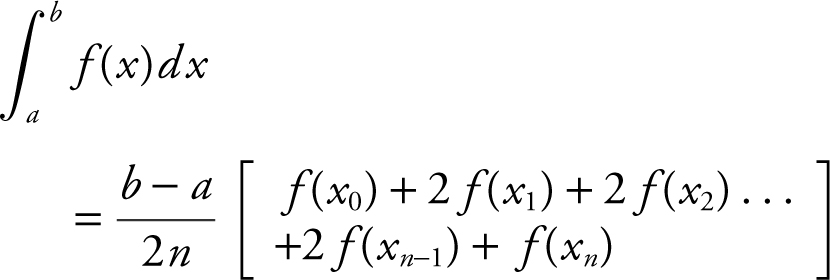
17. Average Value of a Function:
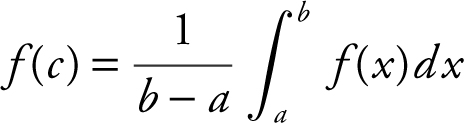
18. Mean Value Theorem:
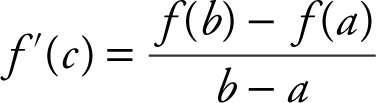for some c in (a , b ).
Mean Value Theorem for Integrals:
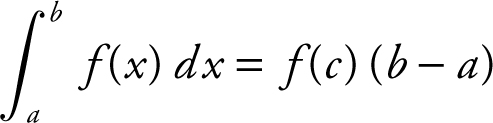for some c in (a , b ).
19. Area Bounded by 2 Curves:
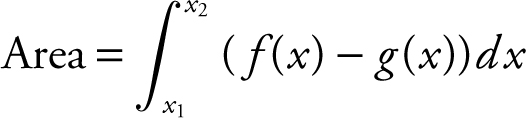
where f (x ) ≥ g (x ).
20. Volume of a Solid with Known Cross Section:
,
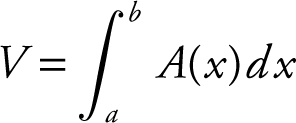where A (x ) is the cross section.
21. Disc Method:
.
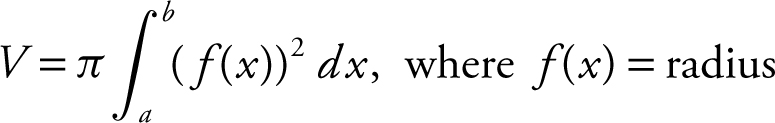22. Using the Washer Method:
,
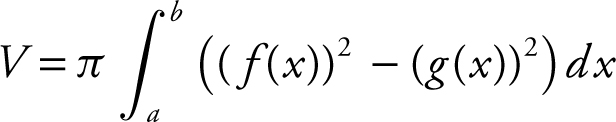where f (x ) = outer radius and g (x ) = inner radius.
23. Distance Traveled Formulas:
• Position Function: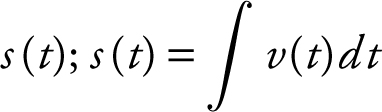
• Velocity: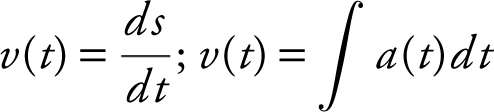
• Acceleration: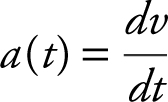
• Speed: |v (t )|
• Displacement from 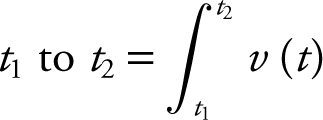= s (t 2 ) – s (t 1 ).
• Total Distance Traveled from t 1 to .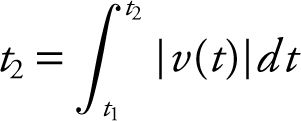
24. Business Formulas:
.
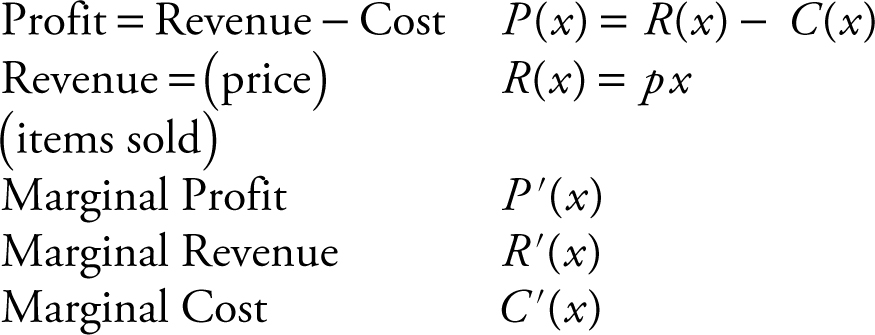P ′(x ), R ′(x ), C ′(x ) are the instantaneous rates of change of profit, revenue, and cost respectively.
25. Exponential Growth/Decay Formulas:
.
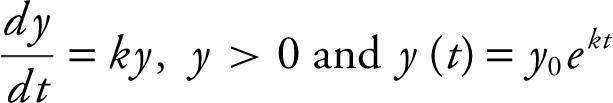