5 Steps to a 5: AP Calculus AB 2017 (2016)
STEP 4
Review the Knowledge You Need to Score High
CHAPTER 8
Big Idea 2: Derivatives
Graphs of Functions and Derivatives
IN THIS CHAPTER
Summary: Many questions on the AP Calculus AB exam involve working with graphs of a function and its derivatives. In this chapter, you will learn how to use derivatives both algebraically and graphically to determine the behavior of a function. Applications of Rolle’s Theorem, the Mean Value Theorem, and the Extreme Value Theorem are also shown.
Key Ideas
![]() Rolle’s Theorem, Mean Value Theorem, and Extreme Value Theorem
Rolle’s Theorem, Mean Value Theorem, and Extreme Value Theorem
![]() Test for Increasing and Decreasing Functions
Test for Increasing and Decreasing Functions
![]() First and Second Derivative Tests for Relative Extrema
First and Second Derivative Tests for Relative Extrema
![]() Test for Concavity and Point of Inflection
Test for Concavity and Point of Inflection
![]() Curve Sketching
Curve Sketching
![]() Graphs of Derivatives
Graphs of Derivatives
8.1 Rolle’s Theorem, Mean Value Theorem, and Extreme Value Theorem
Main Concepts: Rolle’s Theorem, Mean Value Theorem, Extreme Value Theorem

• Set your calculator to Radians and change it to Degrees if/when you need to. Do not forget to change it back to Radians after you have finished using it in Degrees.
Rolle’s Theorem
If f is a function that satisfies the following three conditions:
1. f is continuous on a closed interval [a , b ]
2. f is differentiable on the open interval (a , b )
3. f (a ) = f (b ) = 0
then there exists a number c in (a , b ) such that f ′(c ) = 0. (See Figure 8.1-1 .)
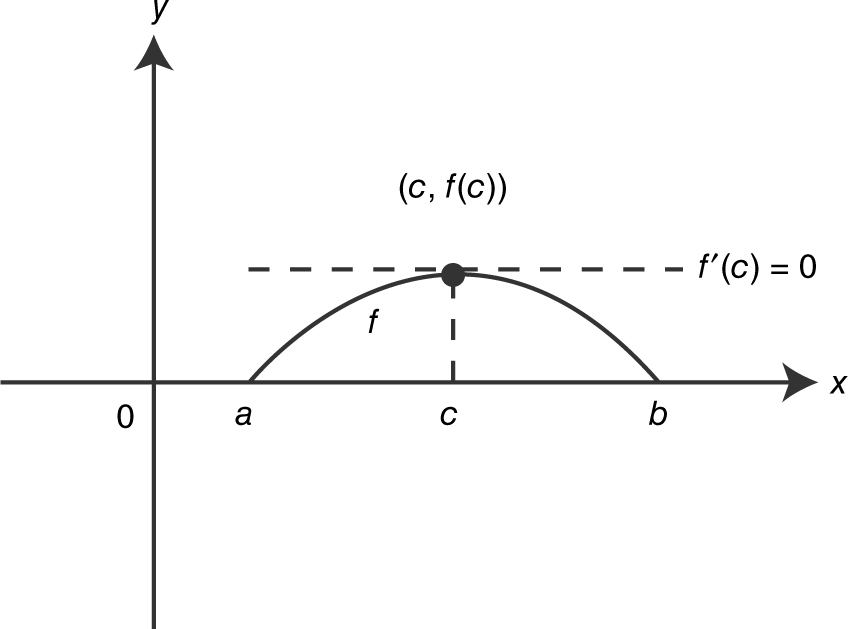
Figure 8.1-1
Note that if you change condition 3 from f (a ) = f (b ) = 0 to f (a ) = f (b ), the conclusion of Rolle’s Theorem is still valid.
Mean Value Theorem
If f is a function that satisfies the following conditions:
1. f is continuous on a closed interval [a , b ]
2. f is differentiable on the open interval (a , b )
then there exists a number c in (a , b ) such that 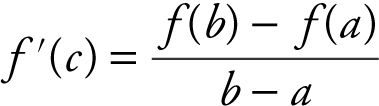 . (See Figure 8.1-2 .)
. (See Figure 8.1-2 .)
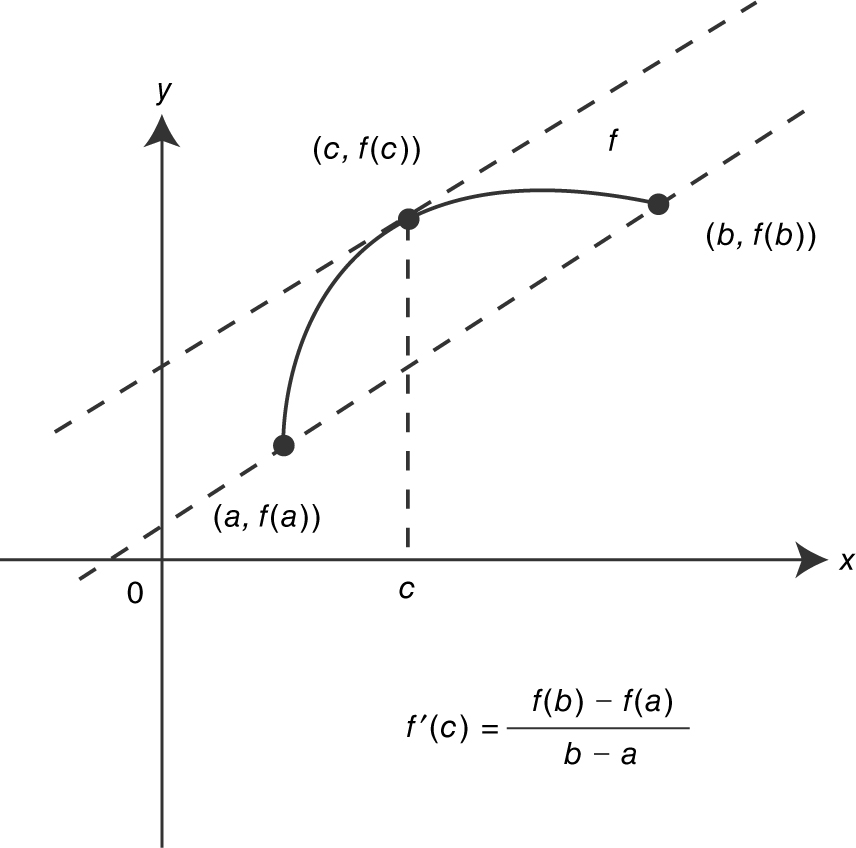
Figure 8.1-2
Example 1
If f (x ) = x 2 + 4x – 5, show that the hypotheses of Rolle’s Theorem are satisfied on the interval [–4, 0] and find all values of c that satisfy the conclusion of the theorem. Check the three conditions in the hypotheses of Rolle’s Theorem:
(1) f (x ) = x 2 + 4x – 5 is continuous everywhere since it is polynomial.
(2) The derivative f ′(x ) = 2x + 4 is defined for all numbers and thus is differentiable on (–4, 0).
(3) f (0) = f (–4) = –5. Therefore, there exists a c in (–4, 0) such that f ′(c ) = 0. To find c , set f ′(x ) = 0. Thus, 2x + 4 = 0 ⇒ x = –2, i.e., f ′(–2) = 0. (See Figure 8.1-3 .)
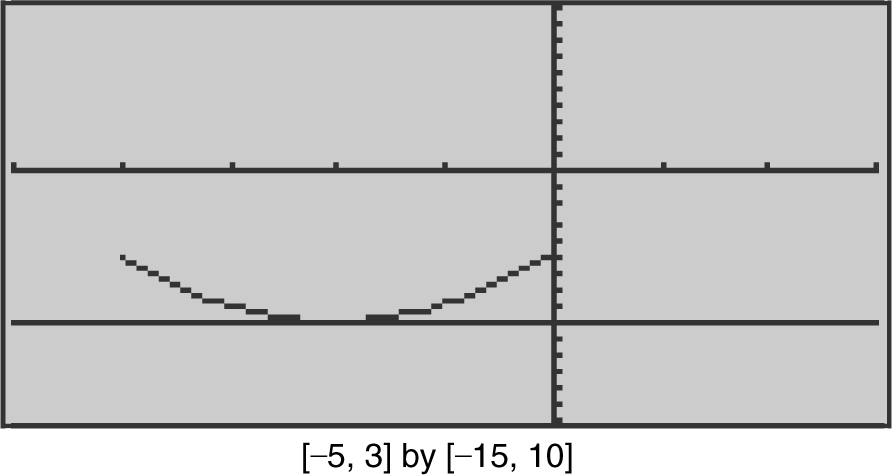
Figure 8.1-3
Example 2
Let 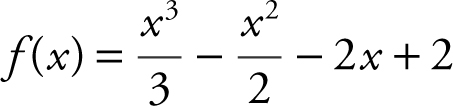 . Using Rolle’s Theorem, show that there exists a number c in the domain of f such that f ′(c ) = 0. Find all values of c .
. Using Rolle’s Theorem, show that there exists a number c in the domain of f such that f ′(c ) = 0. Find all values of c .
Note f (x ) is a polynomial and thus f (x ) is continuous and differentiable everywhere.
Enter 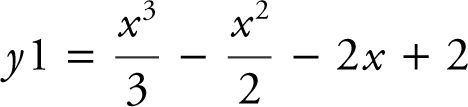 . The zeros of y 1 are approximately –2.3, 0.9, and 2.9 i.e., f (–2.3) = f (0.9) = f (2.9) = 0. Therefore, there exists at least one c in the interval (–2.3, 0.9) and at least one c in the interval (0.9, 2.9) such that f ′(c ) = 0. Use d [Differentiate ] to find f ′(x ): f ′(x ) = x 2 – x – 2. Set f ′(x ) = 0 ⇒ x 2 – x – 2 = 0 or (x – 2)(x + 1) = 0.
. The zeros of y 1 are approximately –2.3, 0.9, and 2.9 i.e., f (–2.3) = f (0.9) = f (2.9) = 0. Therefore, there exists at least one c in the interval (–2.3, 0.9) and at least one c in the interval (0.9, 2.9) such that f ′(c ) = 0. Use d [Differentiate ] to find f ′(x ): f ′(x ) = x 2 – x – 2. Set f ′(x ) = 0 ⇒ x 2 – x – 2 = 0 or (x – 2)(x + 1) = 0.
Thus, x = 2 or x = –1, which implies f ′(2) = 0 and f ′(–1) = 0. Therefore, the values of c are –1 and 2. (See Figure 8.1-4 .)
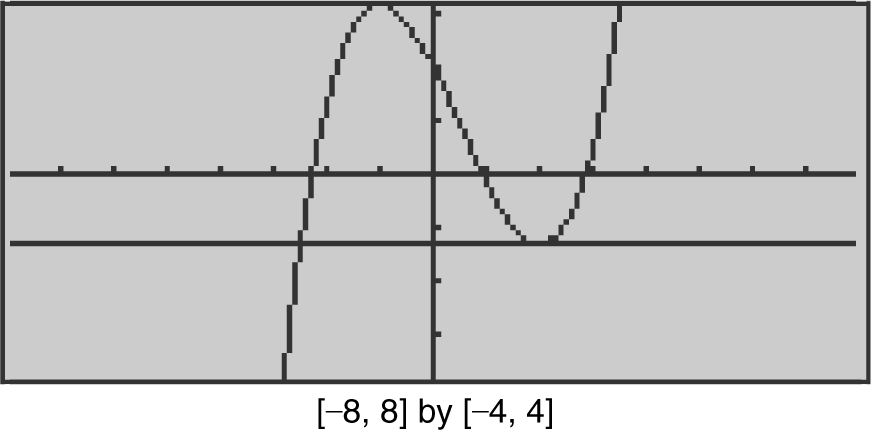
Figure 8.1-4
Example 3
The points P (1, 1) and Q (3, 27) are on the curve f (x ) = x 3 . Using the Mean Value Theorem, find c in the interval (1, 3) such that f ′(c ) is equal to the slope of the secant 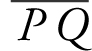 .
.
The slope of secant 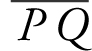 is
is 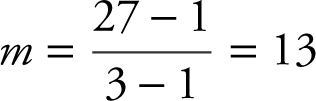 . Since f (x ) is defined for all real numbers, f (x ) is continuous on [1, 3]. Also f ′(x ) = 3x 2 is defined for all real numbers. Thus, f (x ) is differentiable on (1, 3). Therefore, there exists a number c in (1, 3) such that f ′(c ) = 13.
. Since f (x ) is defined for all real numbers, f (x ) is continuous on [1, 3]. Also f ′(x ) = 3x 2 is defined for all real numbers. Thus, f (x ) is differentiable on (1, 3). Therefore, there exists a number c in (1, 3) such that f ′(c ) = 13.
Set f ′(c ) = 13 ⇒ 3(c )2 = 13 or 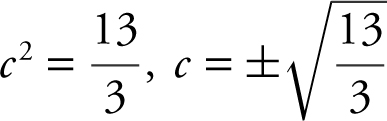 . Since only
. Since only 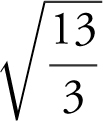 is in the interval (1, 3),
is in the interval (1, 3), 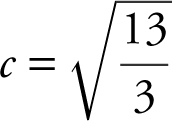 . (See Figure 8.1-5 .)
. (See Figure 8.1-5 .)
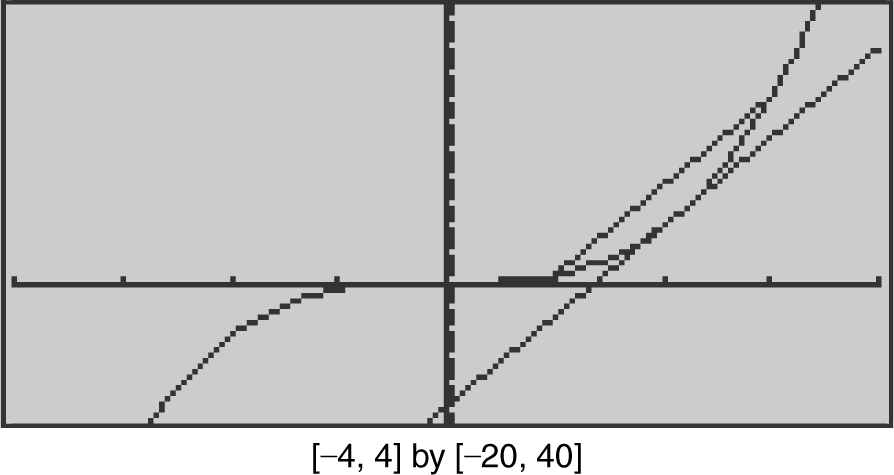
Figure 8.1-5
Example 4
Let f be the function f (x ) = (x – 1)2/3 . Determine if the hypotheses of the Mean Value Theorem are satisfied on the interval [0, 2], and if so, find all values of c that satisfy the conclusion of the theorem.
Enter y 1 = (x – 1)2/3 . The graph y 1 shows that there is a cusp at x = 1. Thus, f (x ) is not differentiable on (0, 2) which implies there may or may not exist a c in (0, 2) such that 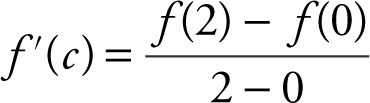 . The derivative
. The derivative 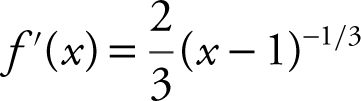 and
and 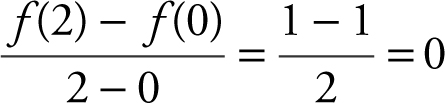 . Set
. Set 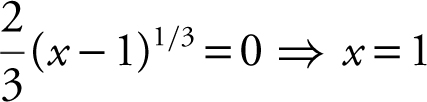 . Note that f is not differentiable (a + x = 1). Therefore, c does not exist. (See Figure 8.1-6 .)
. Note that f is not differentiable (a + x = 1). Therefore, c does not exist. (See Figure 8.1-6 .)
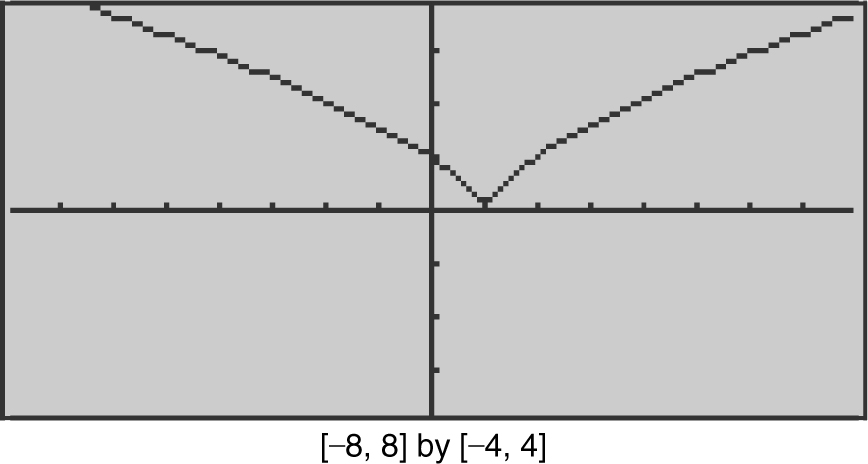
Figure 8.1-6

• The formula for finding the area of an equilateral triangle is 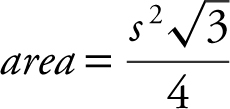 where s is the length of a side. You might need this to find the volume of a solid whose cross sections are equilateral triangles.
where s is the length of a side. You might need this to find the volume of a solid whose cross sections are equilateral triangles.
Extreme Value Theorem
If f is a continuous function on a closed interval [a , b ], then f has both a maximum and a minimum value on the interval.
Example 1
If f (x ) = x 3 + 3x 2 – 1, find the maximum and minimum values of f on [– 2, 2]. Since f (x ) is a polynomial, it is a continuous function everywhere. Enter y 1 = x 3 + 3x 2 – 1. The graph of y 1 indicates that f has a minimum of –1 at x= 0 and a maximum value of 19 at x = 2. (See Figure 8.1-7 .)
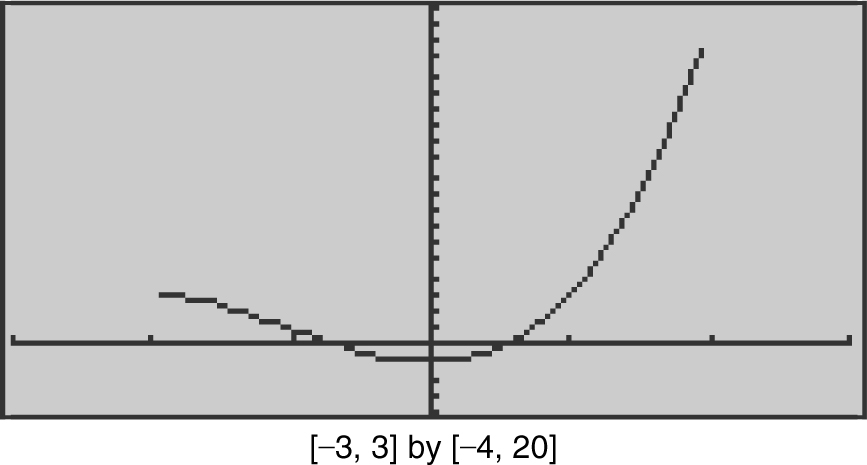
Figure 8.1-7
Example 2
If 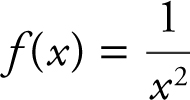 , find any maximum and minimum values of f on [0, 3]. Since f (x ) is a rational function, it is continuous everywhere except at values where the denominator is 0. In this case, at x = 0, f (x ) is undefined. Since f (x ) is not continuous on [0, 3], the Extreme Value Theorem may not be applicable. Enter
, find any maximum and minimum values of f on [0, 3]. Since f (x ) is a rational function, it is continuous everywhere except at values where the denominator is 0. In this case, at x = 0, f (x ) is undefined. Since f (x ) is not continuous on [0, 3], the Extreme Value Theorem may not be applicable. Enter 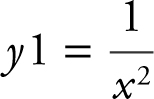 . The graph of y 1 shows that as x → 0+ , f (x ) increases without bound (i.e., f (x ) goes to infinity). Thus, f has no maximum value. The minimum value occurs at the endpoint x = 3 and the minimum value is
. The graph of y 1 shows that as x → 0+ , f (x ) increases without bound (i.e., f (x ) goes to infinity). Thus, f has no maximum value. The minimum value occurs at the endpoint x = 3 and the minimum value is ![]() . (See Figure 8.1-8 .)
. (See Figure 8.1-8 .)
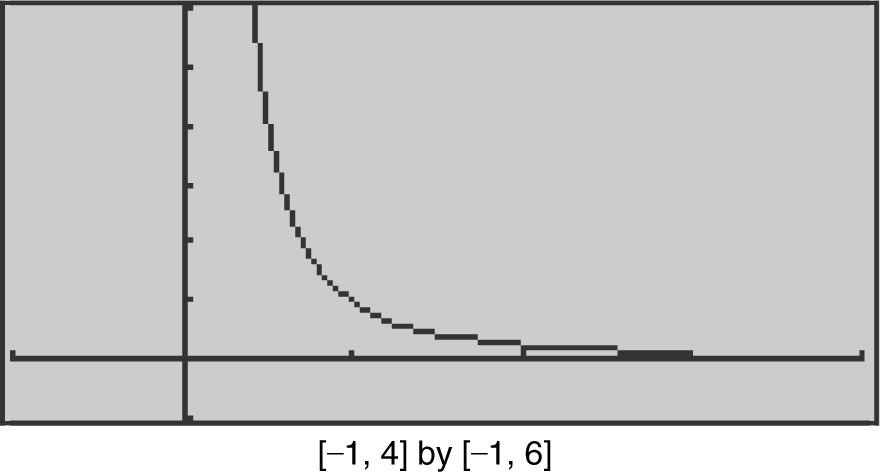
Figure 8.1-8
8.2 Determining the Behavior of Functions
Main Concepts: Test for Increasing and Decreasing Functions, First Derivative Test and Second Derivative Test for Relative Extrema, Test for Concavity and Points of Inflection
Test for Increasing and Decreasing Functions
Let f be a continuous function on the closed interval [a , b ] and differentiable on the open interval (a , b ).
1. If f ′(x ) > 0 on (a , b ), then f is increasing on [a , b ].
2. If f ′(x ) < 0 on (a , b ), then f is decreasing on [a , b ].
3. If f ′(x ) = 0 on (a , b ), then f is constant on [a , b ].
Definition: Let f be a function defined at a number c . Then c is a critical number of f if either f ′(c ) = 0 or f ′ (c ) does not exist. (See Figure 8.2-1 .)
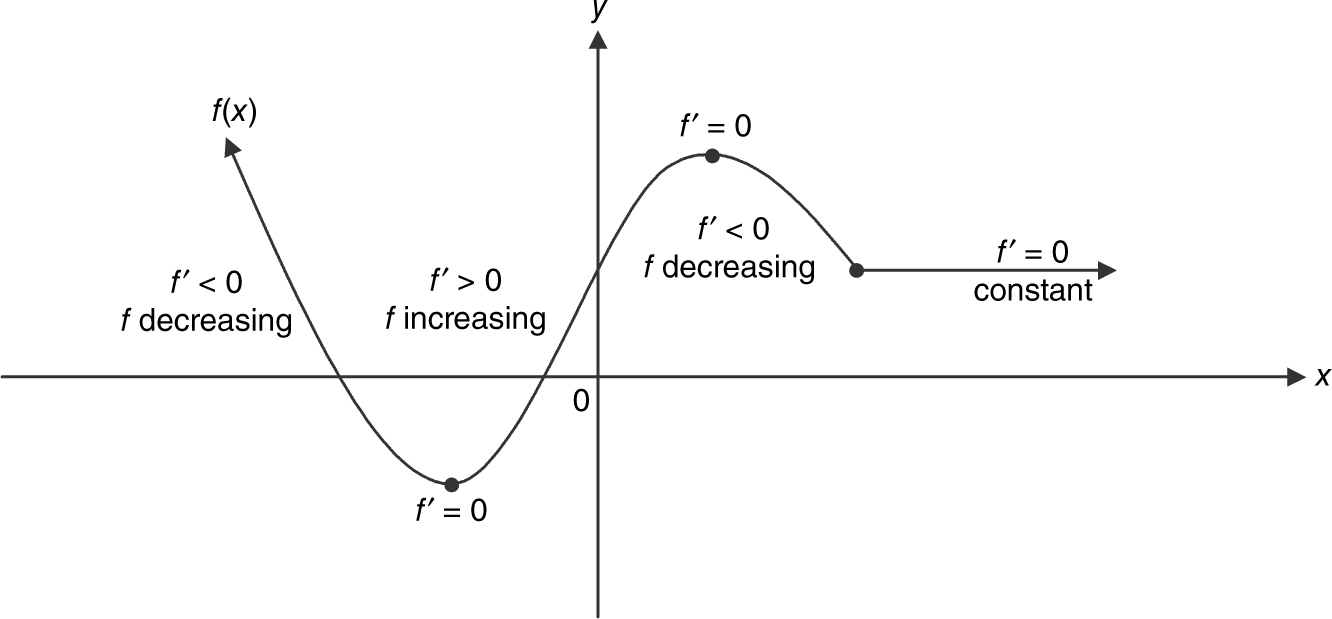
Figure 8.2-1
Example 1
Find the critical numbers of f (x ) = 4x 3 + 2x 2 .
To find the critical numbers of f (x ), you have to determine where f ′(x ) = 0 and where f ′(x ) does not exist. Note f ′(x ) = 12x 2 + 4x , and f ′(x ) is defined for all real numbers. Let f ′(x ) = 0 and thus 12x 2 + 4x = 0, which implies 4x(3x + 1) = 0 ⇒ x = –1/3 or x = 0. Therefore, the critical numbers of f are 0 and –1/3. (See Figure 8.2-2 .)
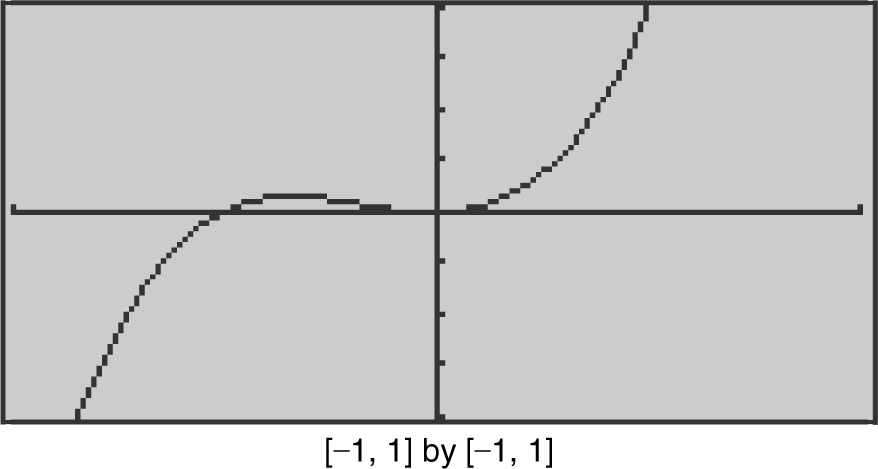
Figure 8.2-2
Example 2
Find the critical numbers of f (x ) = (x – 3)2/5 .
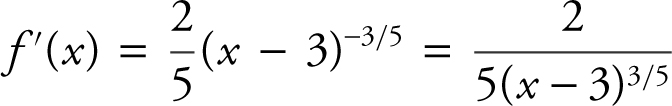 . Note that f ′(x ) is undefined at x = 3 and that f ′(x ) ≠ 0. Therefore, 3 is the only critical number of f . (See Figure 8.2-3 .)
. Note that f ′(x ) is undefined at x = 3 and that f ′(x ) ≠ 0. Therefore, 3 is the only critical number of f . (See Figure 8.2-3 .)
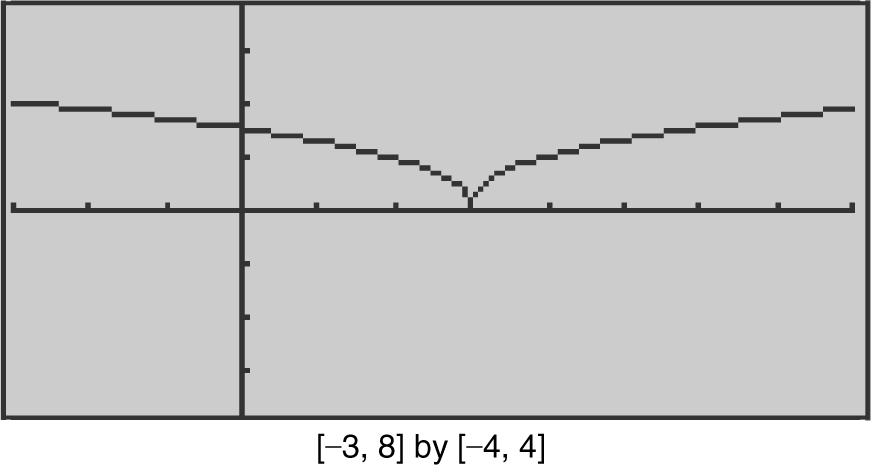
Figure 8.2-3
Example 3
The graph of f ′ on (1, 6) is shown in Figure 8.2-4 . Find the intervals on which f is increasing or decreasing.
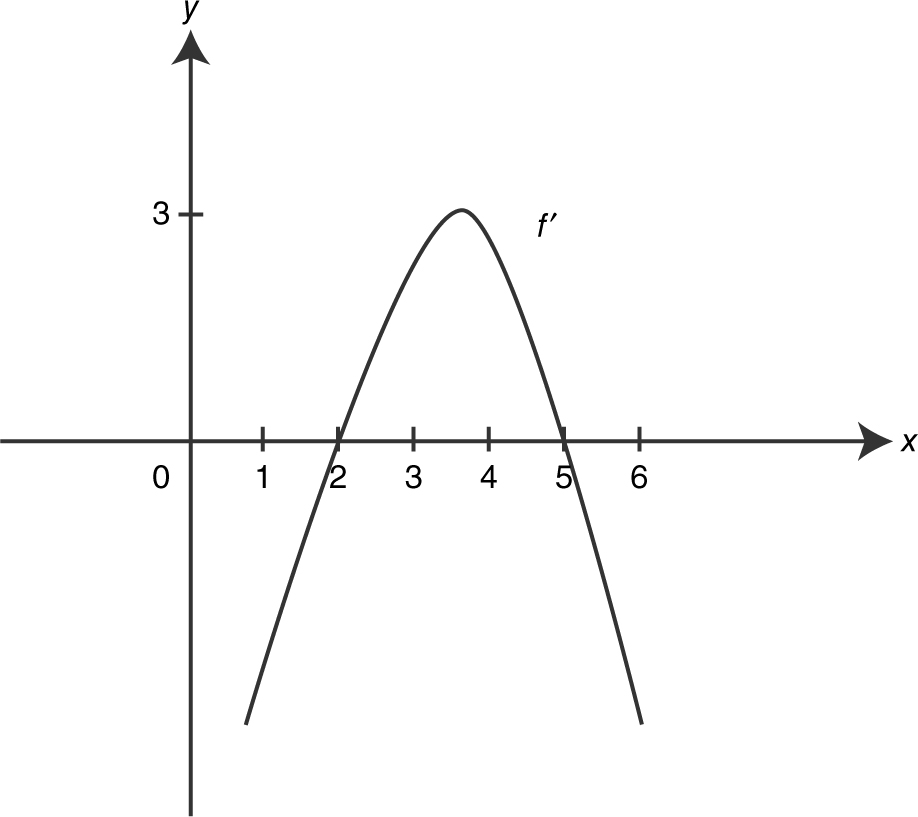
Figure 8.2-4
Solution: (See Figure 8.2-5 .)
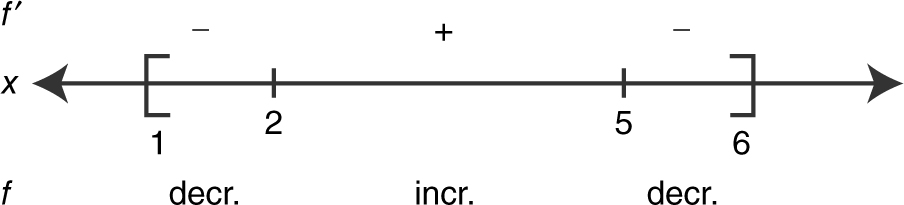
Figure 8.2-5
Thus, f is decreasing on [1, 2] and [5, 6] and increasing on [2, 5].
Example 4
Find the open intervals on which f (x ) = (x 2 – 9)2/3 is increasing or decreasing.
Step 1: Find the critical numbers of f .
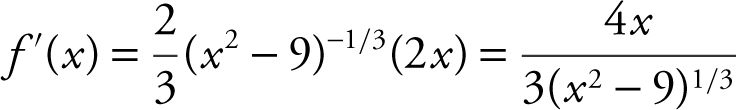
Set f ′(x ) = 0 ⇒ 4x = 0 or x = 0.
Since f ′(x ) is a rational function, f ′(x ) is undefined at values where the denominator is 0. Thus, set x 2 – 9 = 0 ⇒ x = 3 or x = –3. Therefore, the critical numbers are –3, 0, and 3.
Step 2: Determine intervals.
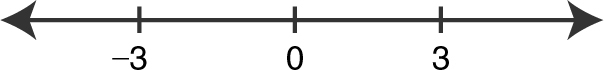
Intervals are (–∞, –3), (–3, 0), (0, 3), and (3, ∞).
Step 3: Set up a table.

Step 4: Write a conclusion. Therefore, f (x ) is increasing on [–3, 0] and [3, ∞) and decreasing on (– ∞, –3] and [0, 3]. (See Figure 8.2-6 .)
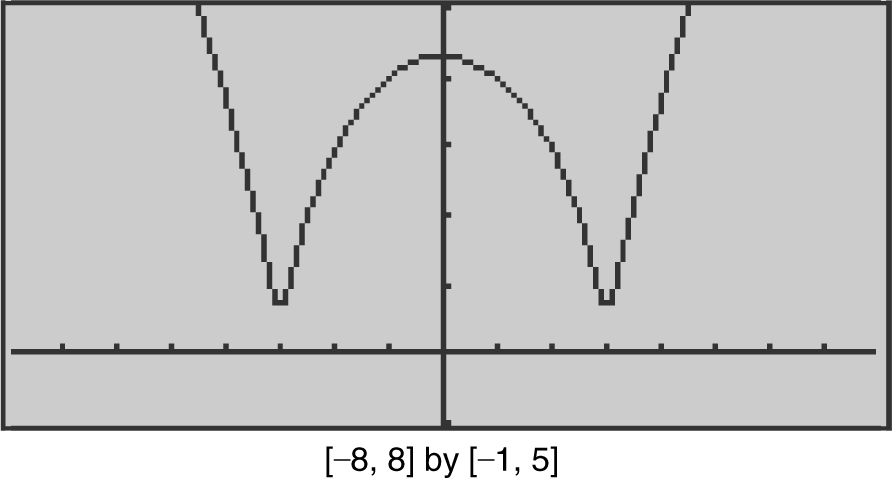
Figure 8.2-6
Example 5
The derivative of a function f is given as f ′(x ) = cos(x 2 ). Using a calculator, find the values of x on 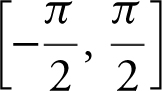 such that f is increasing. (See Figure 8.2-7 .)
such that f is increasing. (See Figure 8.2-7 .)
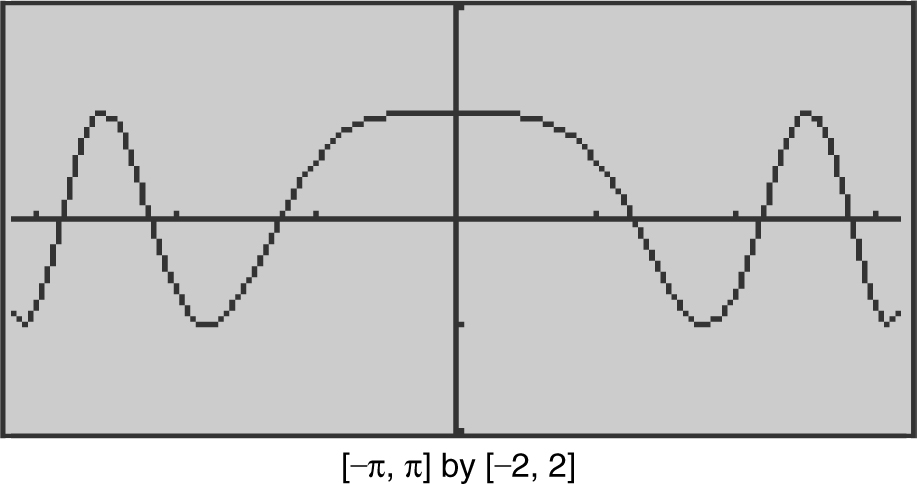
Figure 8.2-7
Using the [Zero ] function of the calculator, you obtain x = 1.25331 is a zero of f ′ on 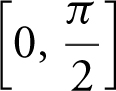 . Since f ′(x ) = cos(x 2 ) is an even function, x = –1.25331 is also a zero on
. Since f ′(x ) = cos(x 2 ) is an even function, x = –1.25331 is also a zero on 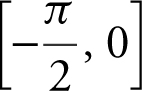 . (See Figure 8.2-8 .)
. (See Figure 8.2-8 .)
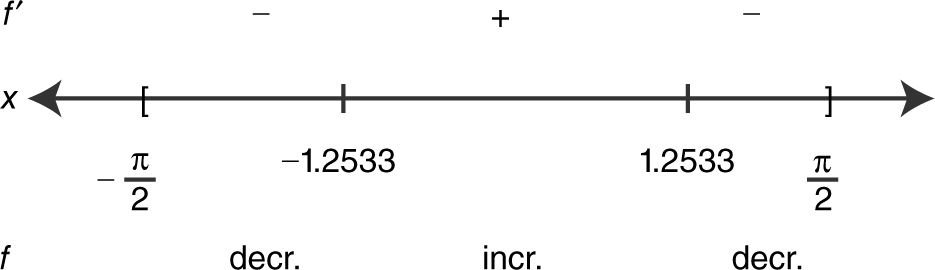
Figure 8.2-8
Thus, f is increasing on [–1.2533, 1.2533].

• Be sure to bubble in the right grid. You have to be careful in filling in the bubbles especially when you skip a question.
First Derivative Test and Second Derivative Test for Relative Extrema
First Derivative Test for Relative Extrema
Let f be a continuous function and c be a critical number of f . (Figure 8.2-9 .)
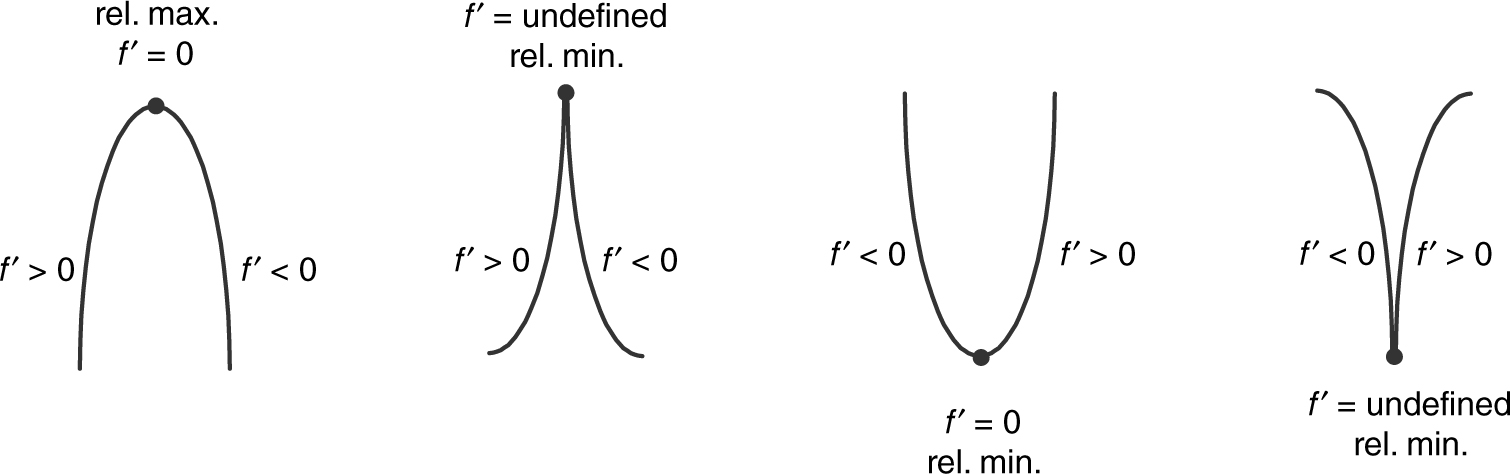
Figure 8.2-9
1. If f ′(x ) changes from positive to negative at x = c (f ′ > 0 for x< c and f ′ < 0 for x > c ), then f has a relative maximum at c .
2. If f ′(x ) changes from negative to positive at x = c (f ′ < 0 for x < c and f ′ > 0 for x > c ), then f has a relative minimum at c .
Second Derivative Test for Relative Extrema
Let f be a continuous function at a number c .
1. If f ′(c ) = 0 and f ″(c ) < 0, then f (c ) is a relative maximum.
2. If f ′(c ) = 0 and f ″(c ) > 0, then f (c ) is a relative minimum.
3. If f ′(c ) = 0 and f ″(c ) = 0, then the test is inconclusive. Use the First Derivative Test.
Example 1
The graph of f ′, the derivative of a function f , is shown in Figure 8.2-10 . Find the relative extrema of f .
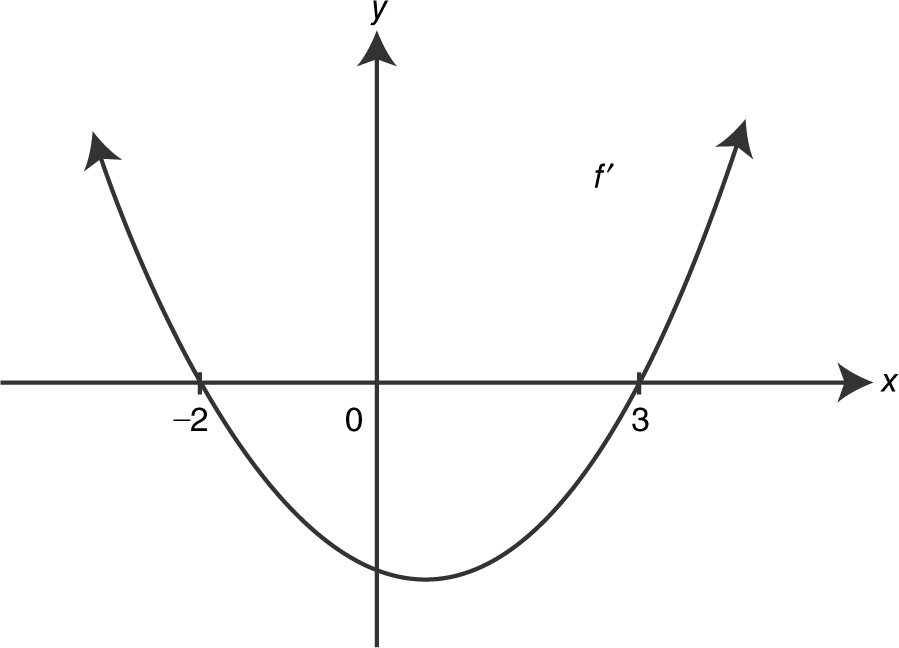
Figure 8.2-10
Solution: (See Figure 8.2-11 .)
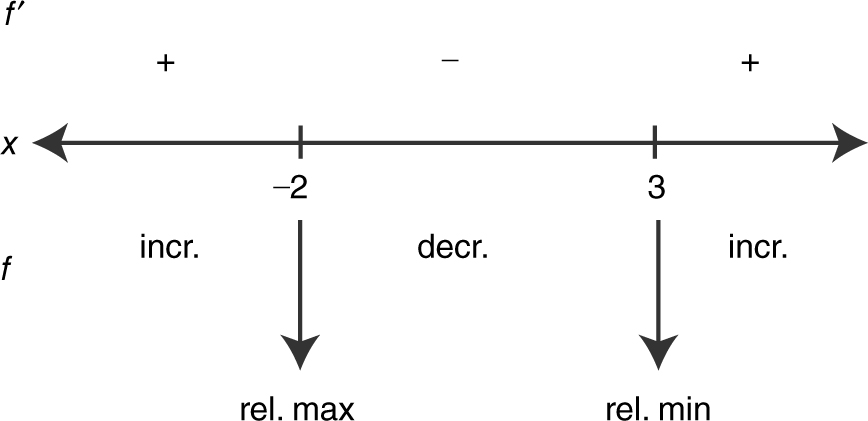
Figure 8.2-11
Thus, f has a relative maximum at x = –2, and a relative minimum at x = 3.
Example 2
Find the relative extrema for the function 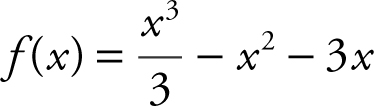 .
.
Step 1: Find f ′(x ).
f ′(x ) = x 2 – 2x – 3
Step 2: Find all critical numbers of f (x ).
Note that f ′(x ) is defined for all real numbers.
Set f ″(x ) = 0: x 2 – 2x – 3 = 0 ⇒ (x – 3)(x + 1) = 0 ⇒ x = 3 or x = –1.
Step 3: Find f ″(x ): f ″ (x ) = 2x – 2.
Step 4: Apply the Second Derivative Test.
f ″(3) = 2(3) – 2 = 4 ⇒ f (3) is a relative minimum.
f ″(–1) = 2(–1) – 2 = –4 ⇒ f (–1) is a relative maximum.
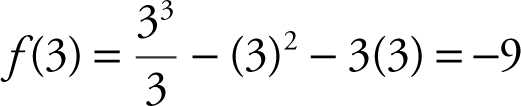 and
and 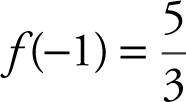 .
.
Therefore, –9 is a relative minimum value of f and ![]() is a relative maximum value. (See Figure 8.2-12 .)
is a relative maximum value. (See Figure 8.2-12 .)
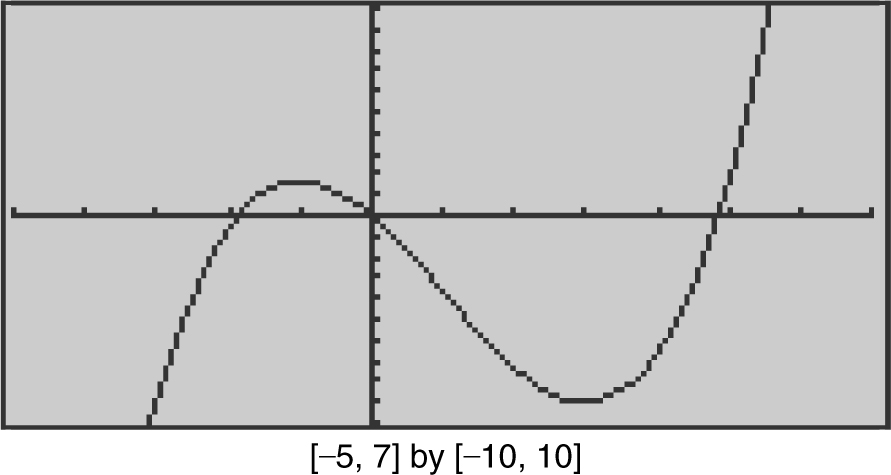
Figure 8.2-12
Example 3
Find the relative extrema for the function f (x ) = (x 2 – 1)2/3 .
Using the First Derivative Test
Step 1: Find f ′(x ).
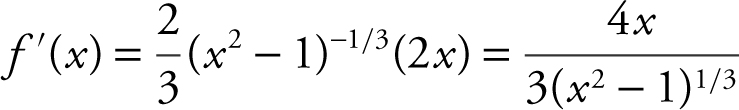
Step 2: Find all critical numbers of f .
Set f ′(x ) = 0. Thus, 4x = 0 or x = 0.
Set x 2 – 1 = 0. Thus, f ′(x ) is undefined at x = 1 and x = –1. Therefore, the critical numbers are –1, 0, and 1.
Step 3: Determine intervals.
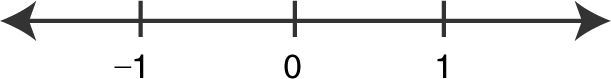
The intervals are (–∞, –1), (–1, 0), (0, 1), and (1, ∞).
Step 4: Set up a table.

Step 5: Write a conclusion.
Using the First Derivative Test, note that f (x ) has a relative maximum at x = 0 and relative minimums at x = –1 and x = 1.
Note that f (–1) = 0, f (0) = 1, and f (1) = 0. Therefore, 1 is a relative maximum value and 0 is a relative minimum value. (See Figure 8.2-13 .)
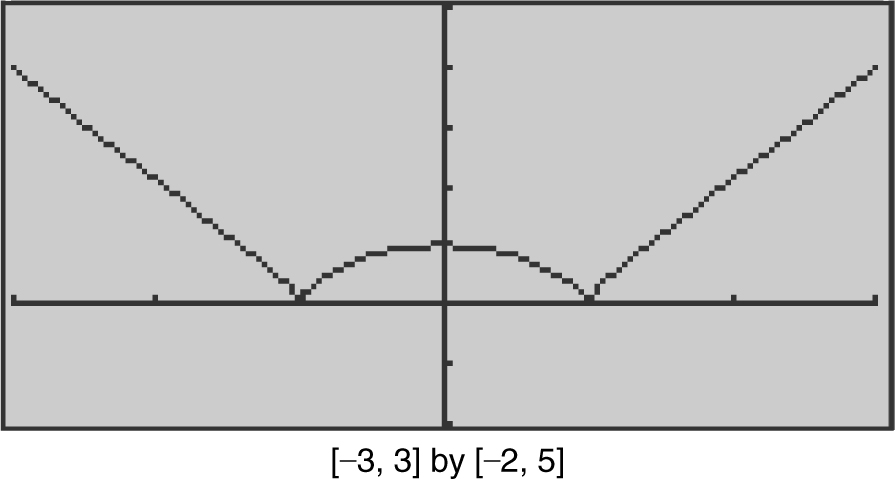
Figure 8.2-13

• Do not forget the constant, C , when you write the antiderivative after evaluating an indefinite integral, e.g., ∫ cos xdx = sin x + C .
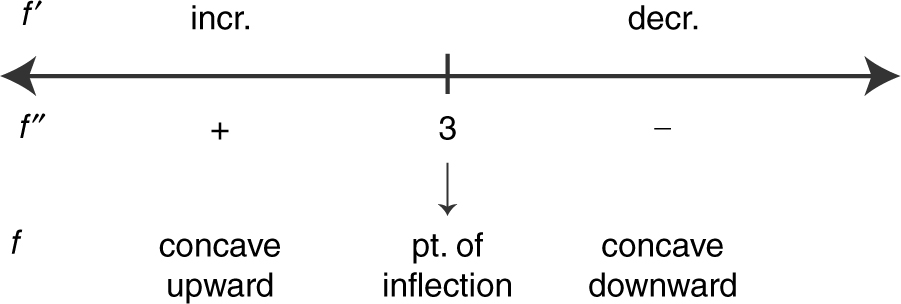
Test for Concavity and Points of Inflection
Test for Concavity
Let f be a differentiable function.
1. If f ″ > 0 on an interval I, then f is concave upward on I.
2. If f ″ < 0 on an interval I, then f is concave downward on I.
(See Figures 8.2-14 and 8.2-15 .)
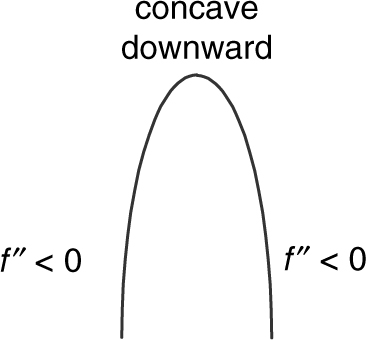
Figure 8.2-14
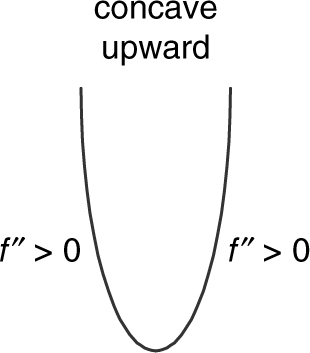
Figure 8.2-15
Points of Inflection
A point P on a curve is a point of inflection if:
1. the curve has a tangent line at P, and
2. the curve changes concavity at P (from concave upward to downward or from concave downward to upward).
(See Figures 8.2-16 –8.2-18 .)
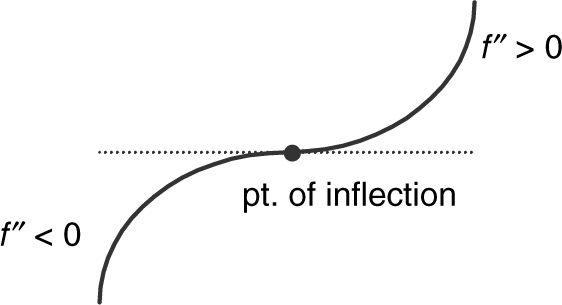
Figure 8.2-16
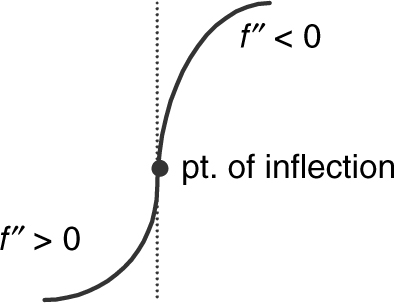
Figure 8.2-17
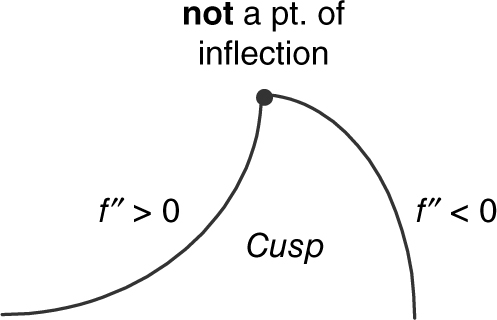
Figure 8.2-18
Note that if a point (a , f (a )) is a point of inflection, then f ″(c ) = 0 or f ″(c ) does not exist. (The converse of the statement is not necessarily true.)
Note: There are some textbooks that define a point of inflection as a point where the concavity changes and do not require the existence of a tangent at the point of inflection. In that case, the point at the cusp in Figure 8.2-18would be a point of inflection.
Example 1
The graph of f ′, the derivative of a function f , is shown in Figure 8.2-19 . Find the points of inflection of f and determine where the function f is concave upward and where it is concave downward on [–3, 5].
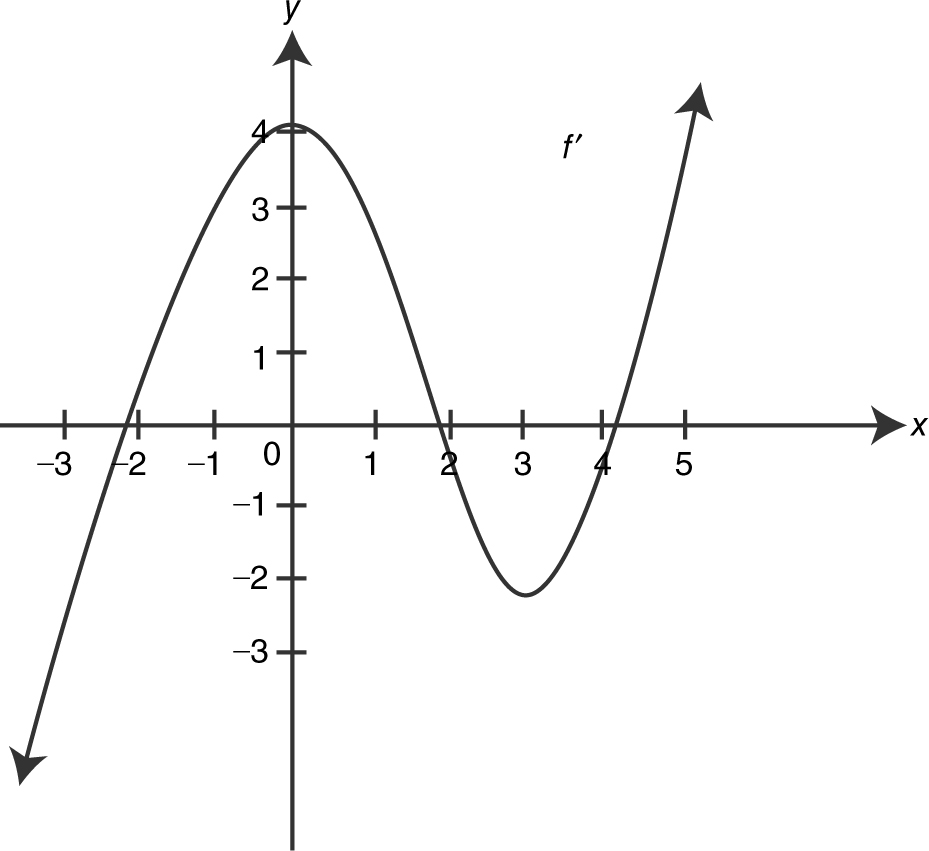
Figure 8.2-19
Solution: (See Figure 8.2-20 .)
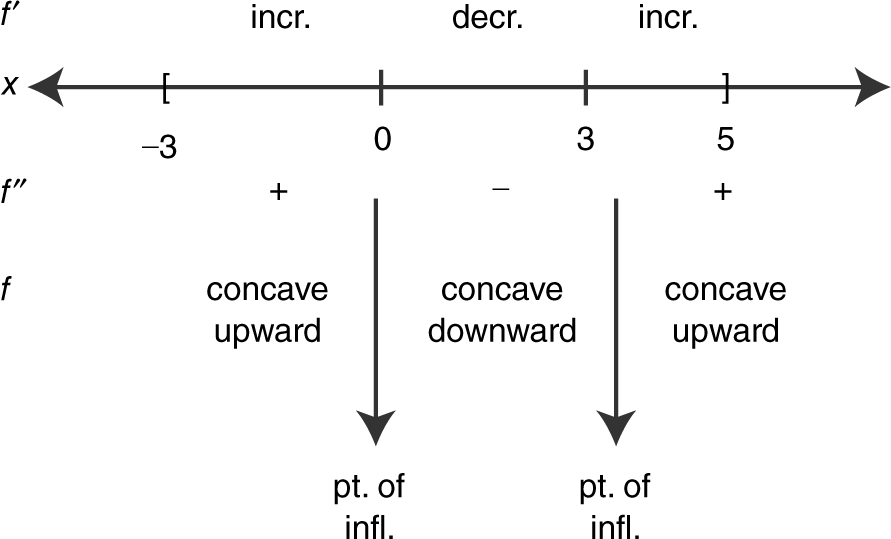
Figure 8.2-20
Thus, f is concave upward on [–3, 0) and (3, 5], and is concave downward on (0, 3).
There are two points of inflection: one at x = 0 and the other at x = 3.
Example 2
Using a calculator, find the values of x at which the graph of y = x 2 e x changes concavity.
Enter y 1 = x ∧ 2 ∗ e ∧ x and y 2 = d (y 1(x ), x , 2). The graph of y 2, the second derivative of y , is shown in Figure 8.2-21 . Using the [Zero ] function, you obtain x = –3.41421 and x = –0.585786. (See Figures 8.2-21 and 8.2-22 .)
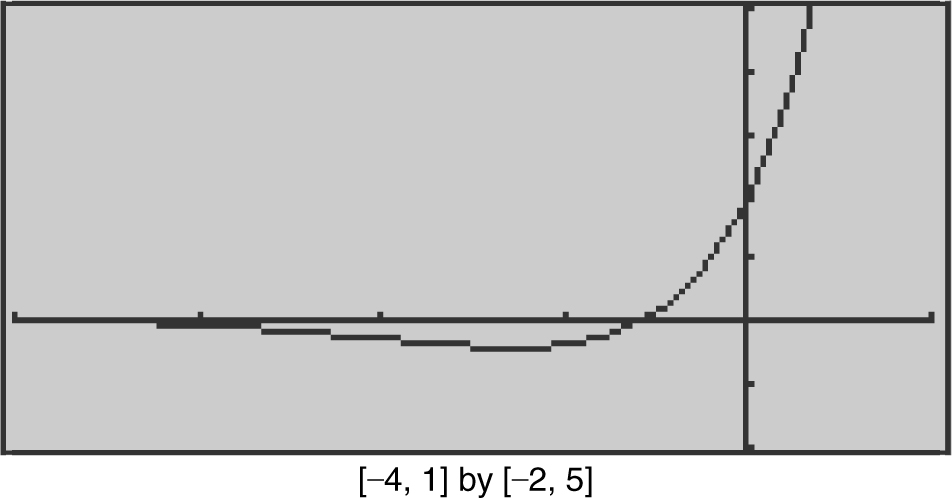
Figure 8.2-21
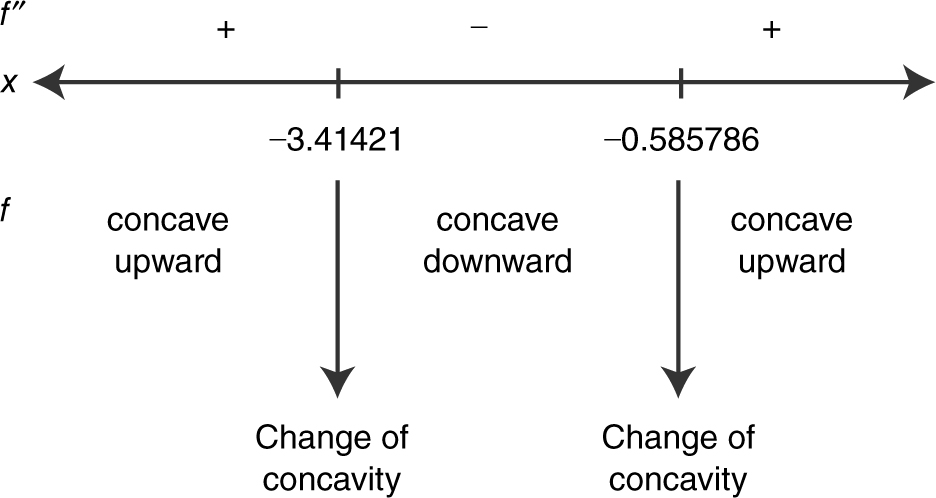
Figure 8.2-22
Thus, f changes concavity at x = –3.41421 and x = –0.585786.
Example 3
Find the points of inflection of f (x ) = x 3 – 6x 2 + 12x – 8 and determine the intervals where the function f is concave upward and where it is concave downward.
Step 1: Find f ′(x ) and f ″(x ).
f ′(x ) = 3x 2 – 12x + 12
f ″(x ) = 6x – 12
Step 2: Set f ″(x ) = 0.
6x – 12 = 0
x = 2
Note that f ″(x ) is defined for all real numbers.
Step 3: Determine intervals.

The intervals are (–∞, 2) and (2, ∞).
Step 4: Set up a table.
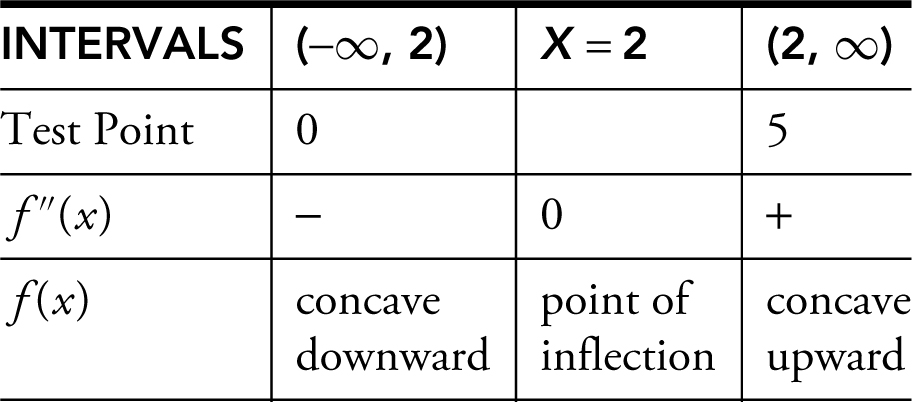
Since f (x ) has change of concavity at x = 2, the point (2, f (2)) is a point of inflection. f (2) = (2)3 – 6(2)2 + 12(2) – 8 = 0.
Step 5: Write a conclusion.
Thus, f (x ) is concave downward on (–∞, 2), concave upward on (2, ∞), and f (x ) has a point of inflection at (2, 0). (See Figure 8.2-23 .)
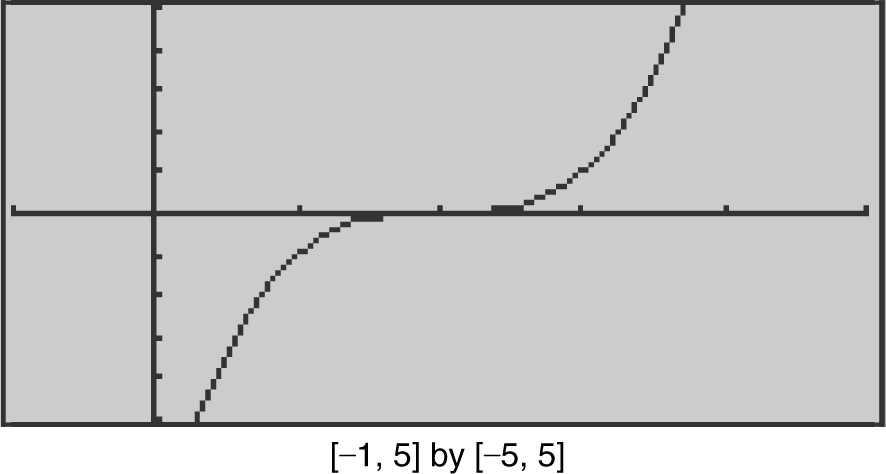
Figure 8.2-23
Example 4
Find the points of inflection of f (x ) = (x – 1)2/3 and determine the intervals where the function f is concave upward and where it is concave downward.
Step 1: Find f ′(x ) and f ″(x ).
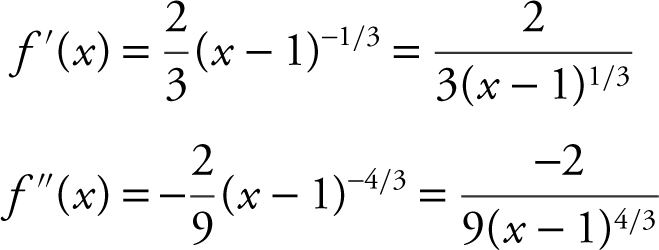
Step 2: Find all values of x where f ″(x ) = 0 or f ″(x ) is undefined.
Note that f ″(x ) ≠ 0 and that f ″(1) is undefined.
Step 3: Determine intervals.
The intervals are (–∞, 1) and (1, ∞).
Step 4: Set up a table.
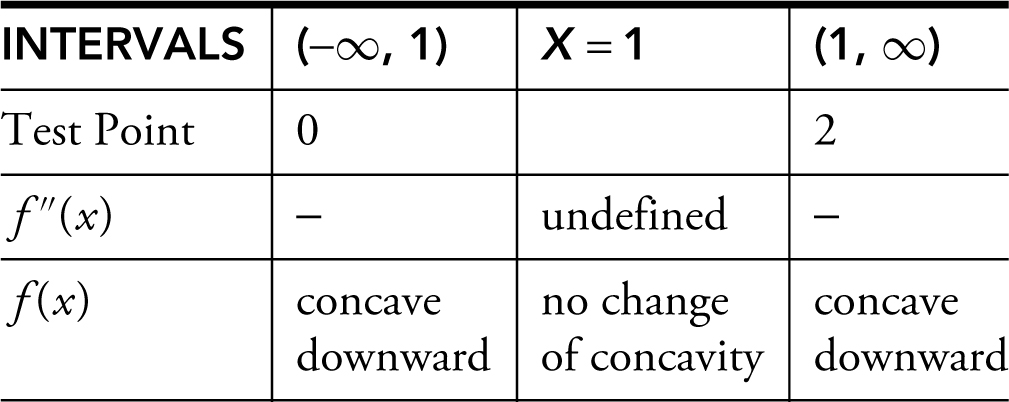
Note that since f (x ) has no change of concavity at x = 1, f does not have a point of inflection.
Step 5: Write a conclusion.
Therefore, f (x ) is concave downward on (–∞, ∞) and has no point of inflection. (See Figure 8.2-24 .)
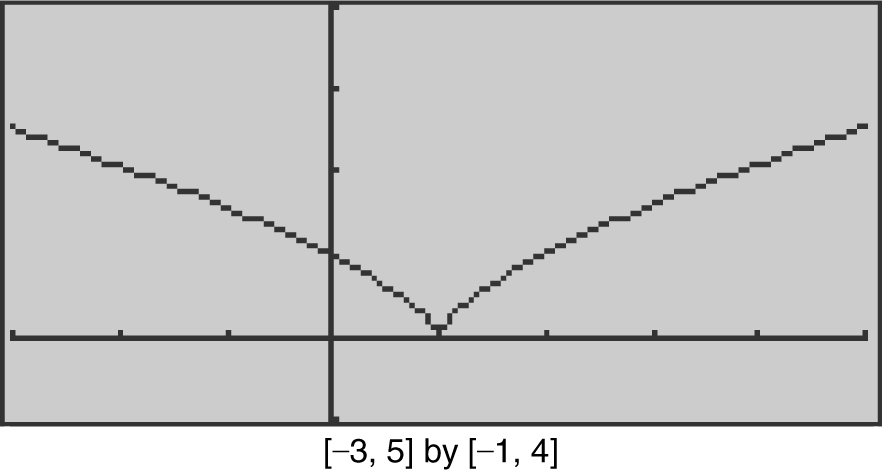
Figure 8.2-24
Example 5
The graph of f is shown in Figure 8.2-25 and f is twice differentiable. Which of the following statements is true?
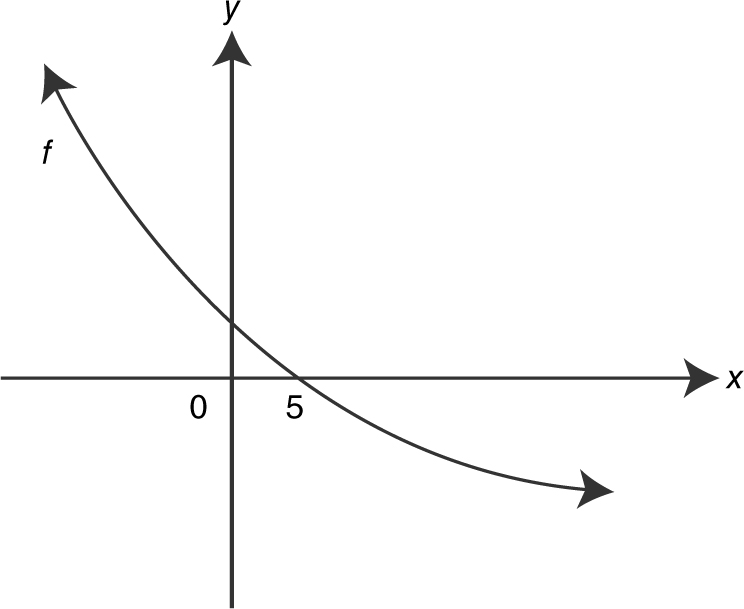
Figure 8.2-25
(A) f (5) < f ′(5) < f ″(5)
(B) f ″(5) < f ′(5) < f (5)
(C) f ′(5) < f (5) < f ″(5)
(D) f ′(5) < f ″(5) < f (5)
The graph indicates that (1) f (5) = 0; (2) f ′(5) < 0, since f is decreasing; and (3) f ″(5) > 0, since f is concave upward. Thus, f ′(5) < f (5) < f ″(5), choice (C).

• Move on. Do not linger on a problem too long. Make an educated guess. You can earn many more points from other problems.
8.3 Sketching the Graphs of Functions
Main Concepts: Graphing without Calculators, Graphing with Calculators
Graphing without Calculators
General Procedure for Sketching the Graph of a Function

Steps:
1. Determine the domain and if possible the range of the function f (x ).
2. Determine if the function has any symmetry, i.e., if the function is even (f (x ) = f (–x )), odd (f (x ) = –f (–x )), or periodic (f (x + p ) = f (x )).
3. Find f ′(x ) and f ″(x ).
4. Find all critical numbers (f ′(x ) = 0 or f ′(x ) is undefined) and possible points of inflection (f ″(x ) = 0 or f ″(x ) is undefined).
5. Using the numbers in Step 4, determine the intervals on which to analyze f (x ).
6. Set up a table using the intervals, to
(a) determine where f (x ) is increasing or decreasing.
(b) find relative and absolute extrema.
(c) find points of inflection.
(d) determine the concavity of f (x ) on each interval.
7. Find any horizontal, vertical, or slant asymptotes.
8. If necessary, find the x -intercepts, the y -intercepts, and a few selected points.
9. Sketch the graph.
Example 1
Sketch the graph of 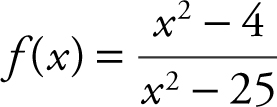 .
.
Step 1: Domain: all real numbers x ≠ ± 5.
Step 2: Symmetry: f (x ) is an even function (f (x ) = f (–x )); symmetrical with respect to the y -axis.
Step 3: 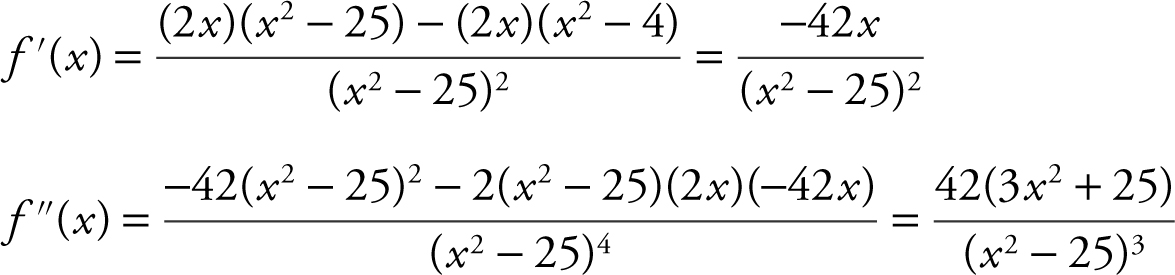
Step 4: Critical numbers:
f ′(x ) = 0 ⇒ –42x = 0 or x = 0
f ′(x ) is undefined at x = ±5 which are not in the domain.
Possible points of inflection:
f ″(x ) ≠ 0 and f ″(x ) is undefined at x = ±5 which are not in the domain.
Step 5: Determine intervals:
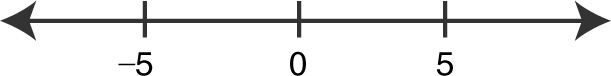
Intervals are (–∞, –5), (–5, 0), (0, 5), and (5, ∞).
Step 6: Set up a table:
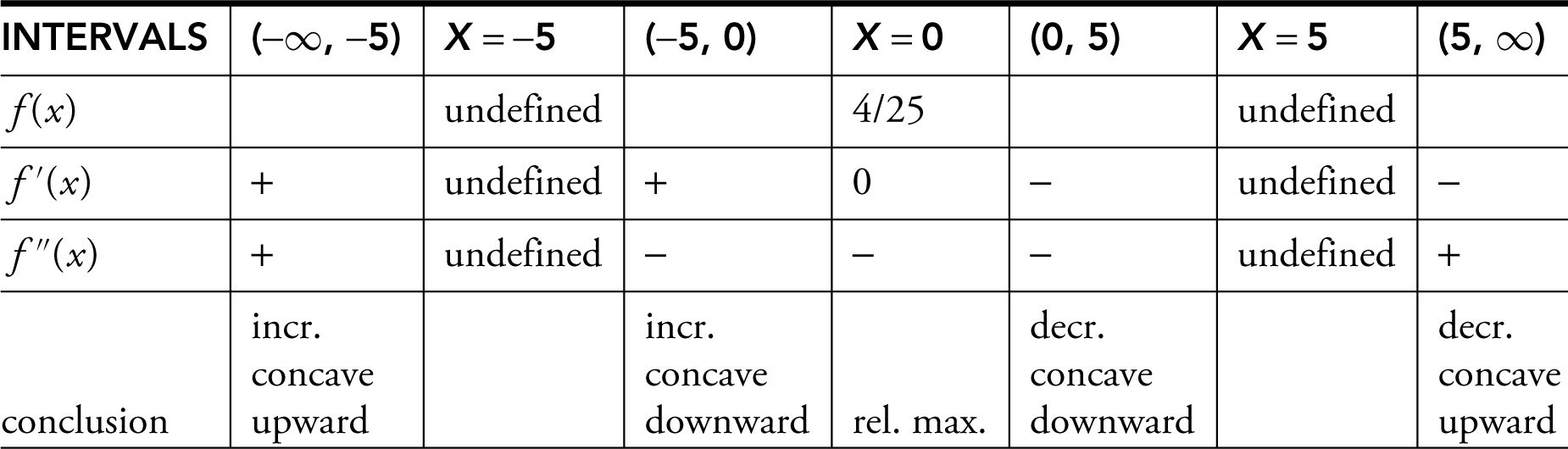
Step 7: Vertical asymptote: x = 5 and x = –5
Horizontal asymptote: y = 1
Step 8: 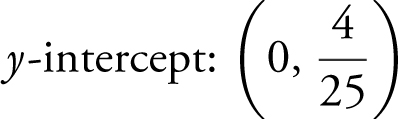
x -intercept: (–2, 0) and (2, 0)
(See Figure 8.3-1 .)
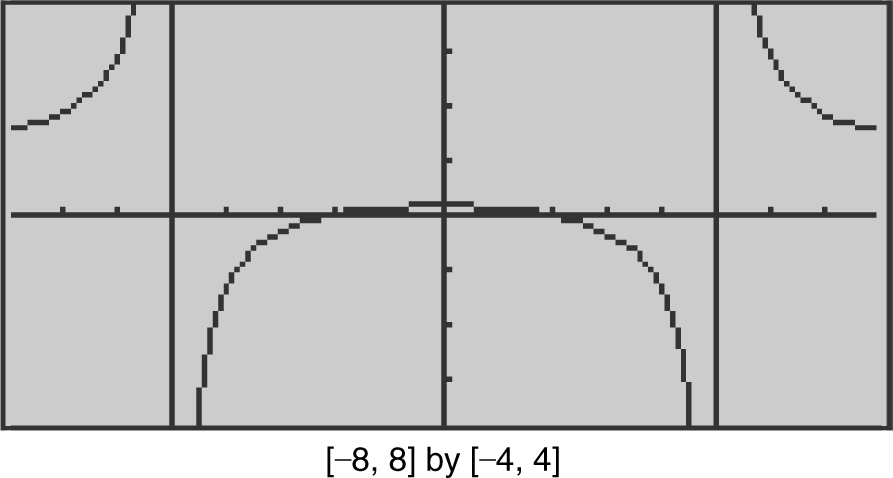
Figure 8.3-1
Graphing with Calculators
Example 1
Using a calculator, sketch the graph of f (x ) = –x 5/3 + 3x 2/3 indicating all relative extrema, points of inflection, horizontal and vertical asymptotes, intervals where f (x ) is increasing or decreasing, and intervals where f (x ) is concave upward or downward.
1. Domain: all real numbers; Range: all real numbers
2. No symmetry
3. Relative maximum: (1.2, 2.03)
Relative minimum: (0, 0)
Points of inflection: (–0.6, 2.56)
4. No asymptote
5. f (x ) is decreasing on (–∞, 0], [1.2, ∞) and increasing on (0, 1.2).
6. Evaluating f ″(x ) on either side of the point of inflection (–0.6, 2.56)
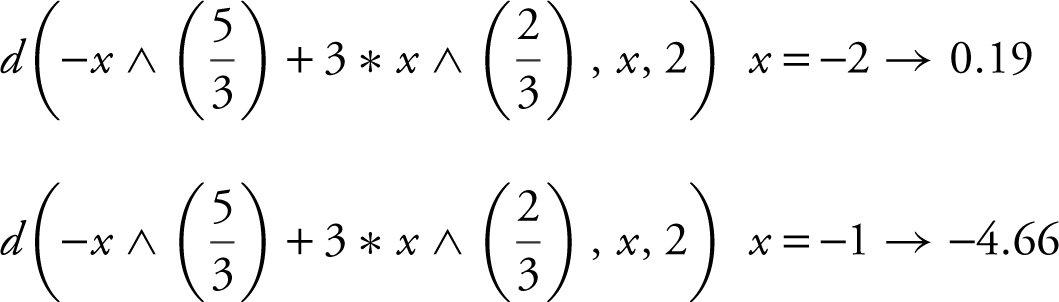
⇒ f (x ) is concave upward on (–∞, –0.6) and concave downward on (–0.6, ∞). (See Figure 8.3-2 .)
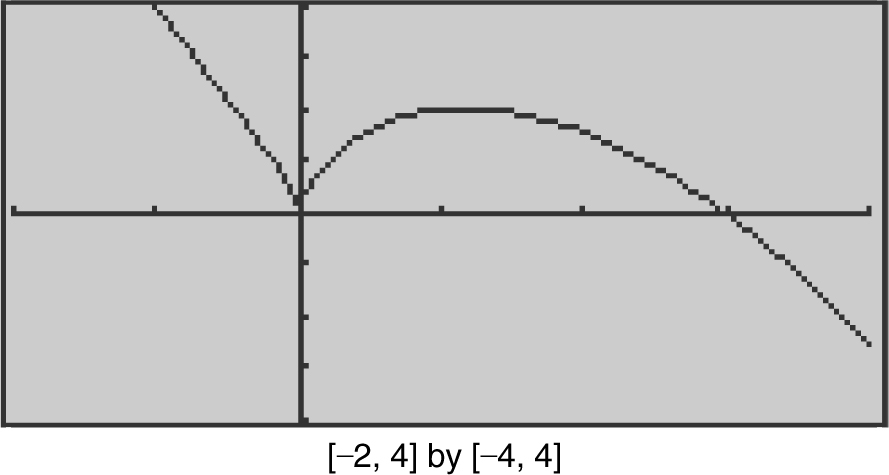
Figure 8.3-2
Example 2
Using a calculator, sketch the graph of f (x ) = e –x 2 /2 , indicating all relative minimum and maximum points; points of inflection; vertical and horizontal asymptotes; and intervals on which f (x ) is increasing, decreasing, concave upward, or concave downward.
1. Domain: all real numbers; Range (0, 1]
2. Symmetry: f (x ) is an even function, and thus is symmetrical with respect to the y -axis.
3. Relative maximum: (0, 1)
No relative minimum
Points of inflection: (–1, 0.6) and (1, 0.6)
4. y = 0 is a horizontal asymptote; no vertical asymptote.
5. f (x ) is increasing on (–∞, 0] and decreasing on [0, ∞).
6. f (x ) is concave upward on (–∞, –1) and (1, ∞); and concave downward on (–1, 1).
(See Figure 8.3-3 .)
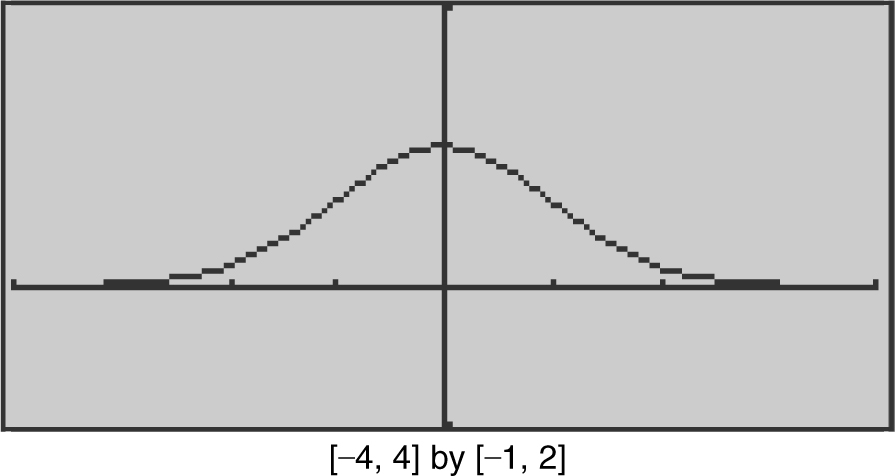
Figure 8.3-3

• When evaluating a definite integral, you do not have to write a constant C , e.g., 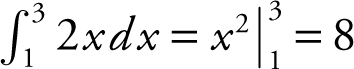 . Notice, no C .
. Notice, no C .
8.4 Graphs of Derivatives
The functions f , f ′, and f ″ are interrelated, and so are their graphs. Therefore, you can usually infer from the graph of one of the three functions (f , f ′, or f ″) and obtain information about the other two. Here are some examples.
Example 1
The graph of a function f is shown in Figure 8.4-1 . Which of the following is true for f on (a , b )?
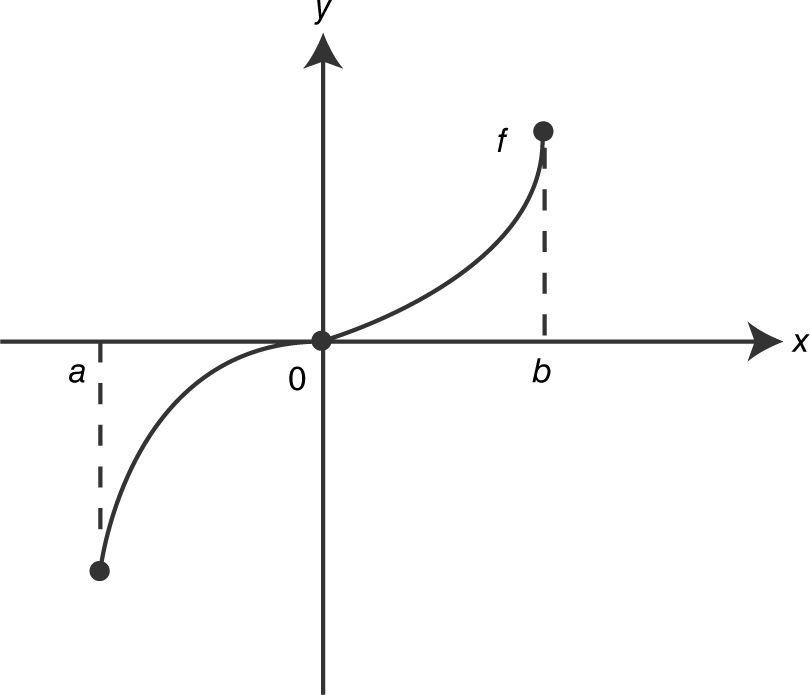
Figure 8.4-1
I. f ′ ≥ 0 on (a , b )
II. f ″ > 0 on (a , b )
Solution:
I. Since f is strictly increasing, f ′ ≥ 0 on (a , b ) is true.
II. The graph is concave downward on (a , 0) and upward on (0, b ). Thus, f ″ > 0 on (0, b ) only. Therefore, only statement I is true.
Example 2
Given the graph of f ′ in Figure 8.4-2 , find where the function f : (a) has its relative maximum(s) or relative minimums, (b) is increasing or decreasing, (c) has its point(s) of inflection, (d) is concave upward or downward, and (e) if f(–2) = f (2) = 1 and f (0) = –3, draw a sketch of f .
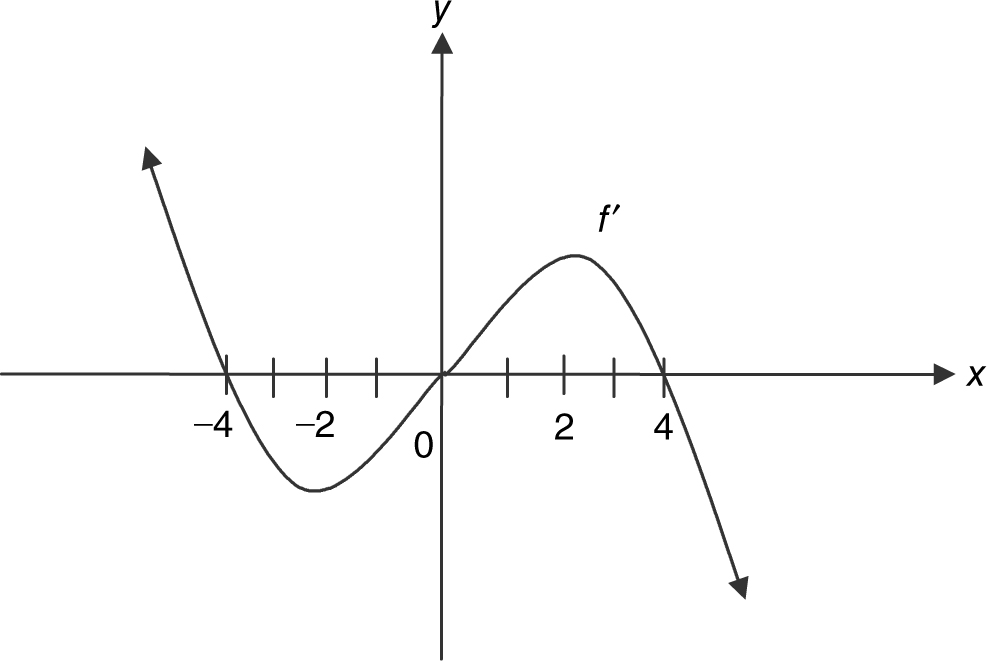
Figure 8.4-2
(a) Summarize the information of f ′ on a number line:
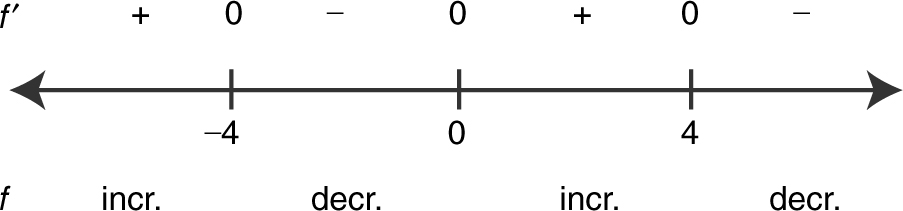
The function f has a relative maximum at x = –4 and at x = 4, and a relative minimum at x = 0.
(b) The function f is increasing on interval (–∞, –4] and [0, 4], and f is decreasing on [–4, 0] and [4, ∞).
(c) Summarize the information of f ″ on a number line:
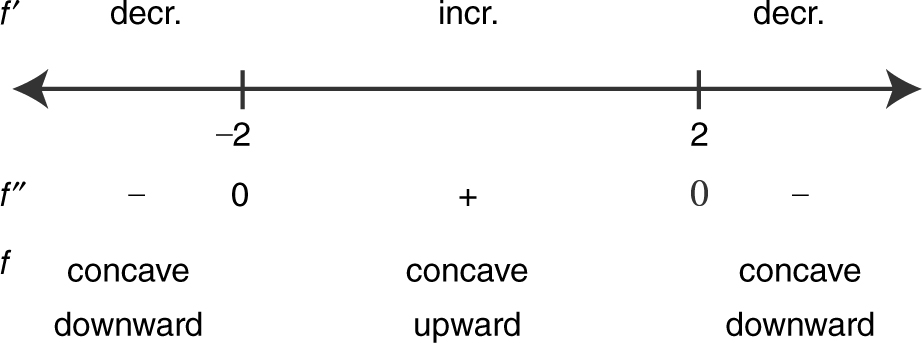
A change of concavity occurs at x = –2 and at x = 2 and f ′ exists at x = –2 and at x = 2, which implies that there is a tangent line to the graph of f at x = –2 and at x = 2. Therefore, f has a point of inflection at x = –2 and at x = 2.
(d) The graph of f is concave upward on the interval (–2, 2) and concave downward on (–∞, –2) and (2, ∞).
(e) A sketch of the graph of f is shown in Figure 8.4-3 .
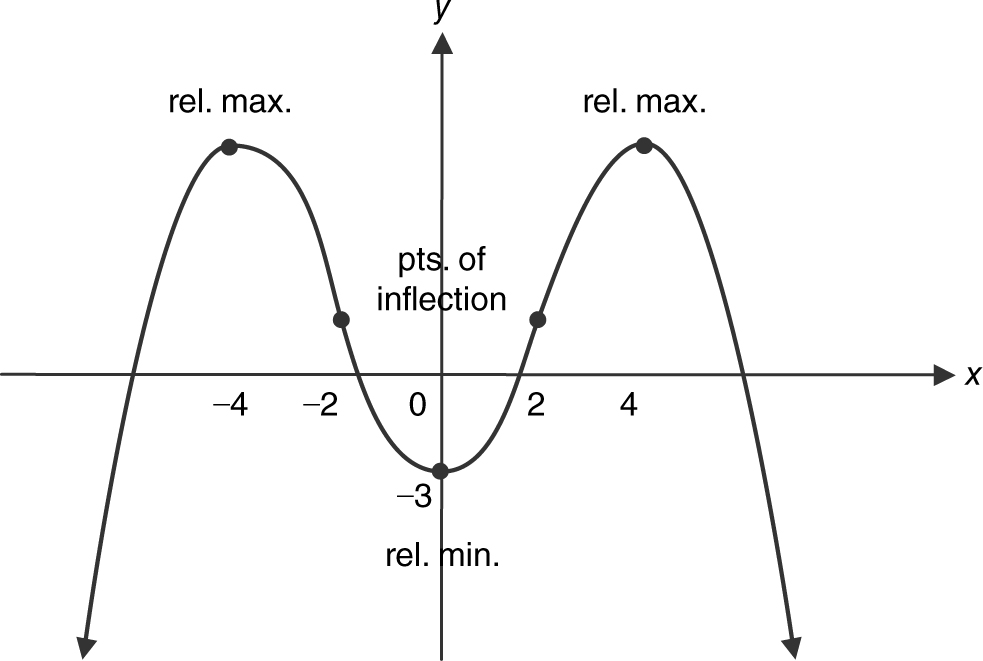
Figure 8.4-3
Example 3
Given the graph of f ′ in Figure 8.4-4 , find where the function f (a) has a horizontal tangent, (b) has its relative extrema, (c) is increasing or decreasing, (d) has a point of inflection, and (e) is concave upward or downward.
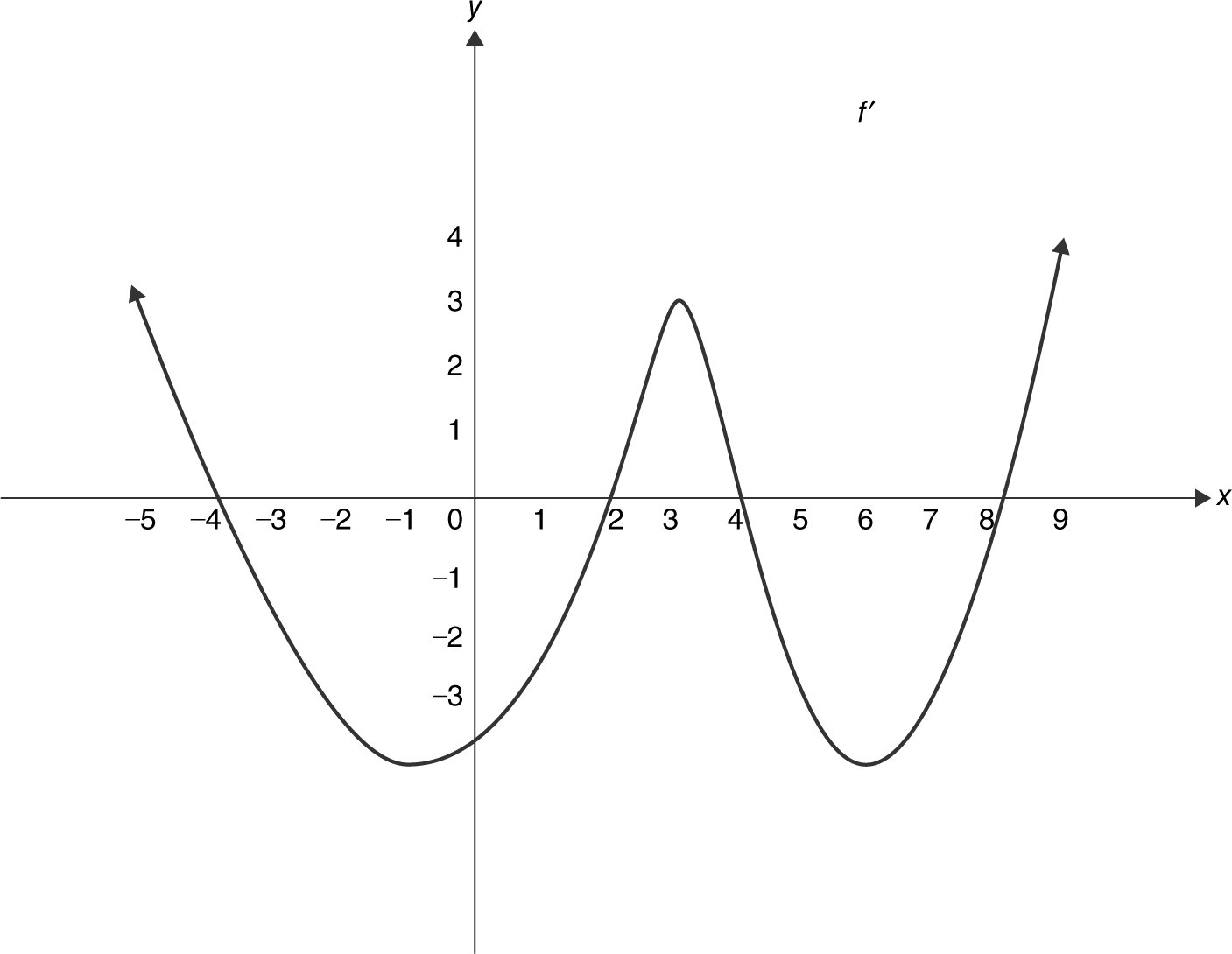
Figure 8.4-4
(a) f ′(x ) = 0 at x = –4, 2, 4, 8. Thus, f has a horizontal tangent at these values.
(b) Summarize the information of f ′ on a number line:
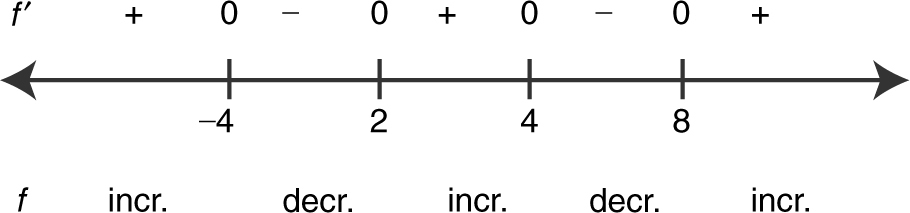
The First Derivative Test indicates that f has relative maximums at x = –4 and 4; and f has relative minimums at x = 2 and 8.
(c) The function f is increasing on (–∞, –4], [2, 4], and [8, ∞) and is decreasing on [–4, 2] and [4, 8].
(d) Summarize the information of f ″ on a number line:
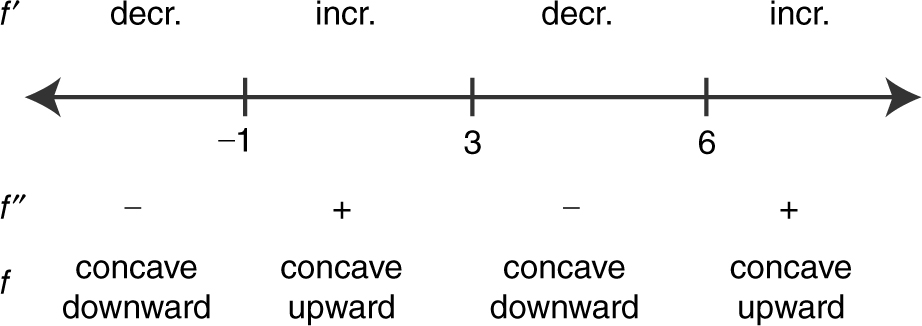
A change of concavity occurs at x = –1, 3, and 6. Since f ′(x ) exists, f has a tangent at every point. Therefore, f has a point of inflection at x = –1, 3, and 6.
(e) The function f is concave upward on (–1, 3) and (6, ∞) and concave downward on (–∞, –1) and (3, 6).
Example 4
A function f is continuous on the interval [–4, 3] with f (–4) = 6 and f (3) = 2 and the following properties:
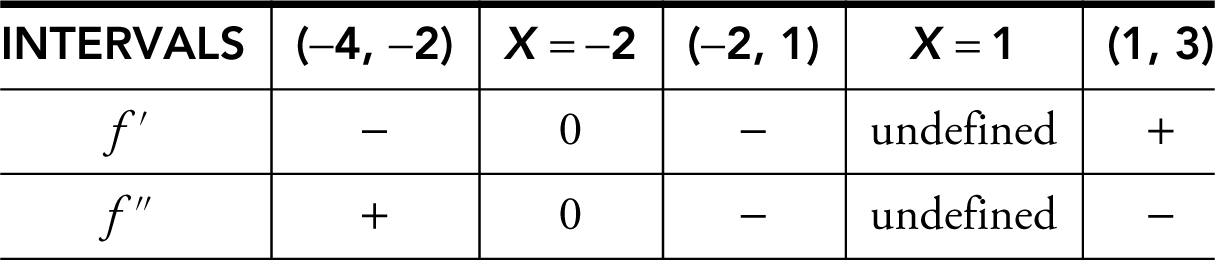
(a) Find the intervals on which f is increasing or decreasing.
(b) Find where f has its absolute extrema.
(c) Find where f has the points of inflection.
(d) Find the intervals where f is concave upward or downward.
(e) Sketch a possible graph of f .
Solution:
(a) The graph of f is increasing on [1, 3] since f ′ > 0 and decreasing on [–4, –2] and [–2, 1] since f ′ < 0.
(b) At x = –4, f (x ) = 6. The function decreases until x = 1 and increases back to 2 at x = 3. Thus, f has its absolute maximum at x = –4 and its absolute minimum at x = 1.
(c) A change of concavity occurs at x = –2, and since f ′(–2) = 0, which implies a tangent line exists at x = –2, f has a point of inflection at x = –2.
(d) The graph of f is concave upward on (–4, –2) and concave downward on (–2, 1) and (1, 3).
(e) A possible sketch of f is shown in Figure 8.4-5 .
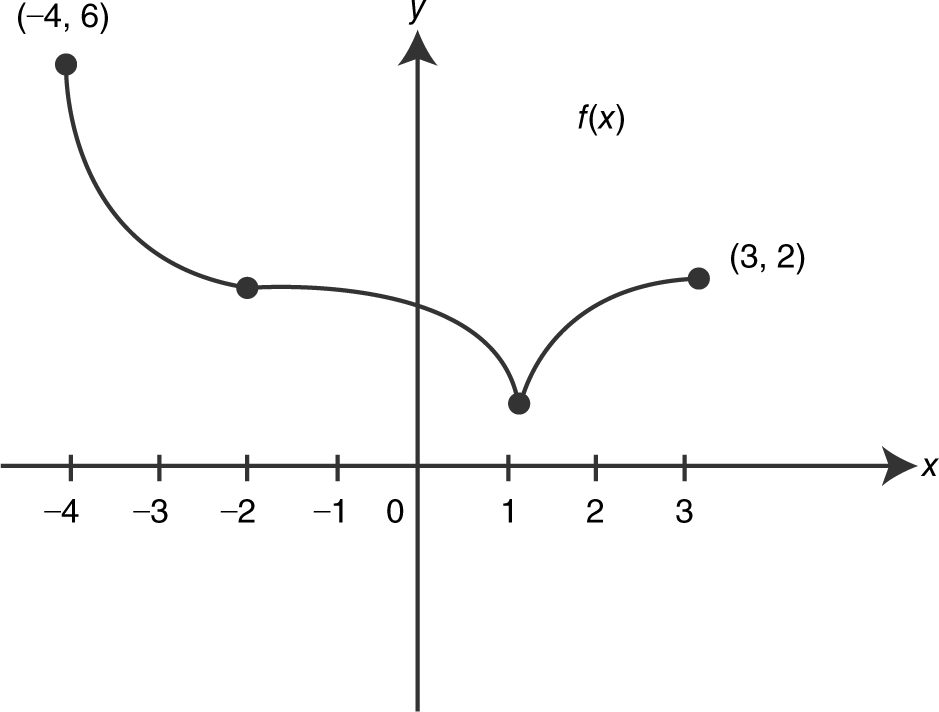
Figure 8.4-5
Example 5
If f (x ) = |ln(x + 1)|, find 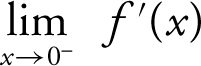 . (See Figure 8.4-6 .)
. (See Figure 8.4-6 .)
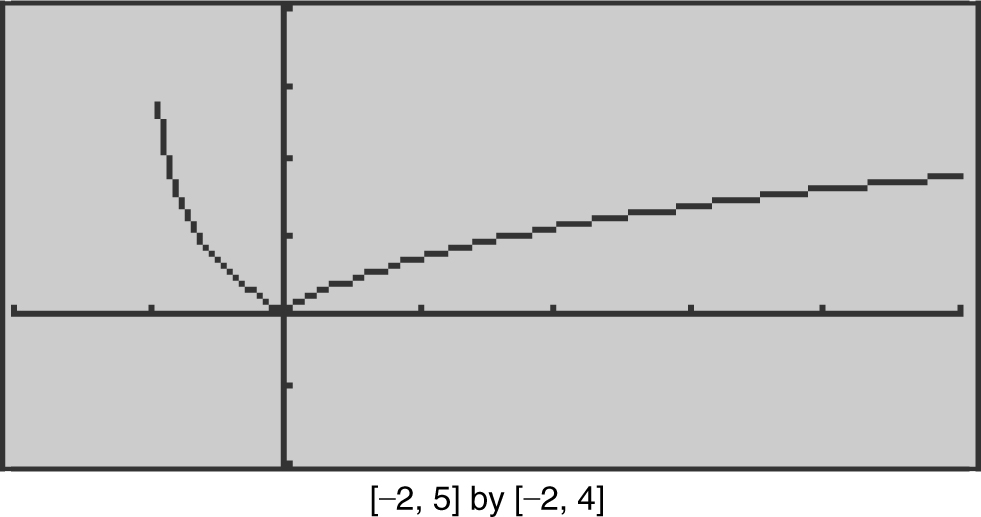
Figure 8.4-6
The domain of f is (–1, ∞).
f (0) = |ln(0 + 1)| = |ln(1)| = 0
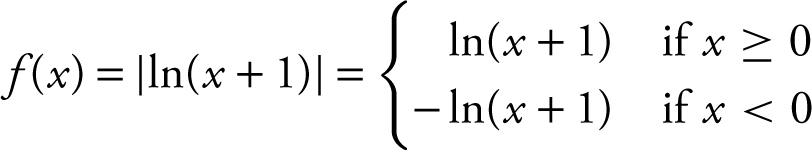
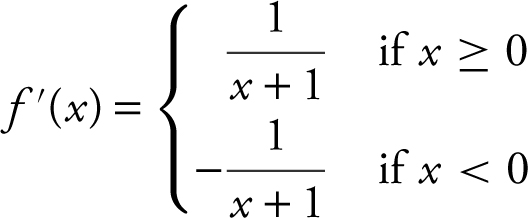
Therefore, 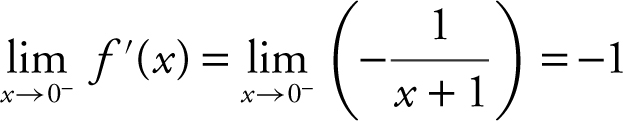 .
.
8.5 Rapid Review
1. If f ′(x ) = x 2 – 4, find the intervals where f is decreasing. (See Figure 8.5-1 .)
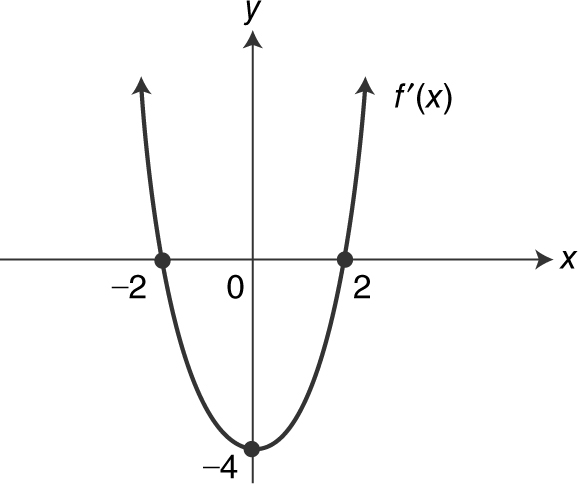
Figure 8.5-1
Answer: Since f ′(x ) < 0 if –2 < x < 2, f is decreasing on (–2, 2).
2. If f ″(x ) = 2x – 6 and f ′ is continuous, find the values of x where f has a point of inflection. (See Figure 8.5-2 .)
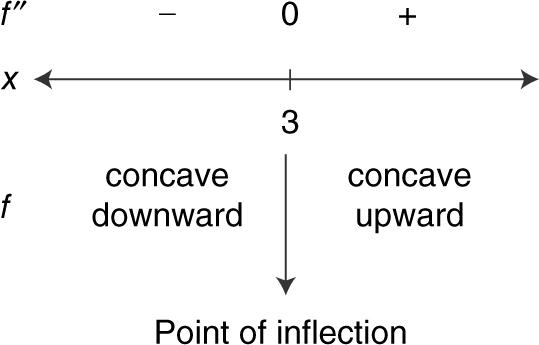
Figure 8.5-2
Answer: Thus, f has a point of inflection at x = 3.
3. (See Figure 8.5-3 .) Find the values of x where f has change of concavity.
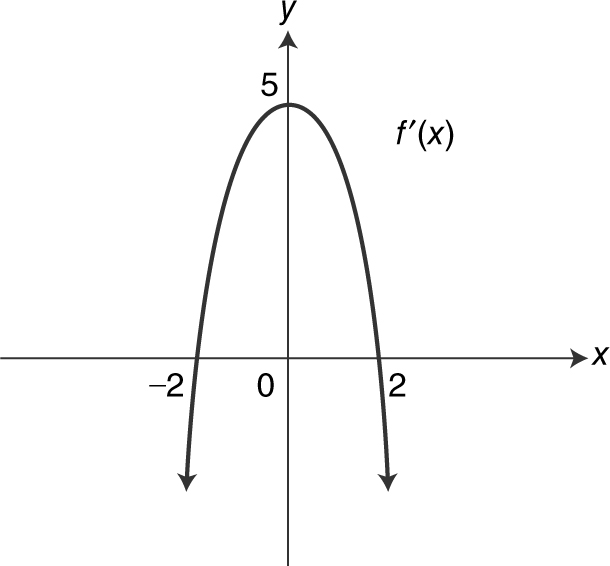
Figure 8.5-3
Answer: f has a change of concavity at x = 0. (See Figure 8.5-4 .)
Figure 8.5-4
4. (See Figure 8.5-5 .) Find the values of x where f has a relative minimum.
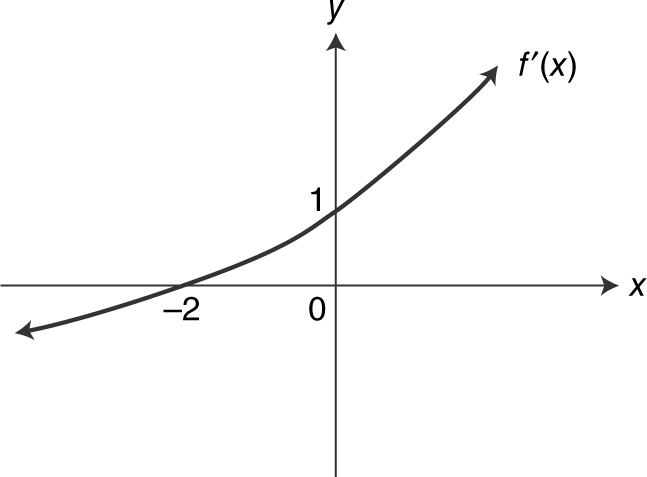
Figure 8.5-5
Answer: f has a relative minimum at x = –2. (See Figure 8.5-6 .)
Figure 8.5-6
5. (See Figure 8.5-7 .) Given f is twice differentiable, arrange f (10), f ′(10), f ″(10) from smallest to largest.
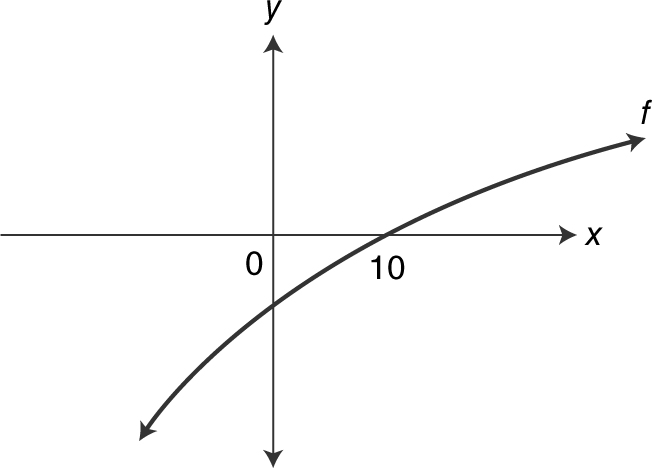
Figure 8.5-7
Answer: f (10) = 0, f ′(10) > 0 since f is increasing, and f ″(10) < 0 since f is concave downward. Thus, the order is f ″(10), f (10), f ′(10).
6. (See Figure 8.5-8 .) Find the values of x where f ′ is concave up.
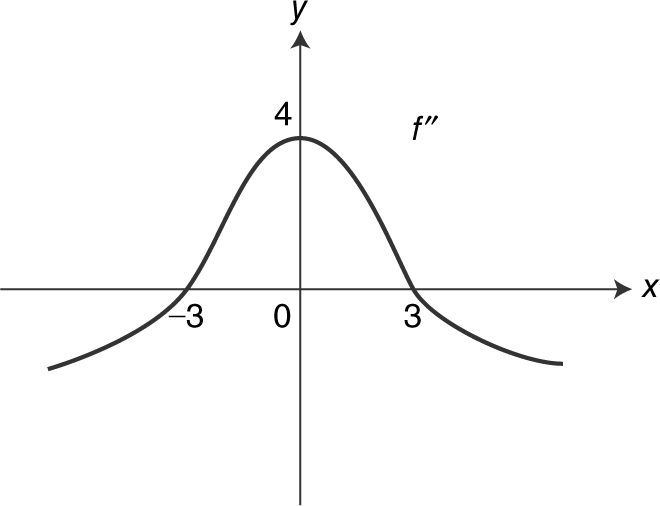
Figure 8.5-8
Answer: f ′ is concave upward on (–∞, 0). (See Figure 8.5-9 .)
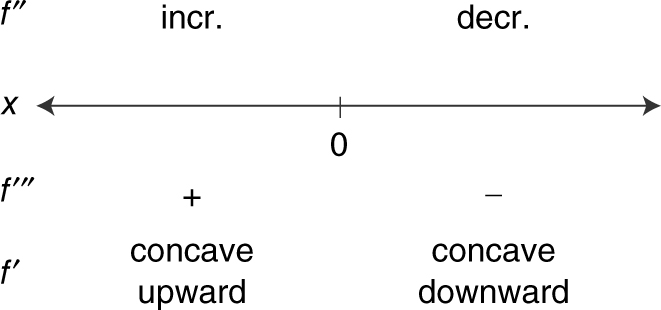
Figure 8.5-9
8.6 Practice Problems
Part A The use of a calculator is not allowed.
1 . If f (x ) = x 3 – x 2 – 2x , show that the hypotheses of Rolle’s Theorem are satisfied on the interval [–1, 2] and find all values of c that satisfy the conclusion of the theorem.
2 . Let f (x ) = e x . Show that the hypotheses of the Mean Value Theorem are satisfied on [0, 1] and find all values of c that satisfy the conclusion of the theorem.
3 . Determine the intervals in which the graph of 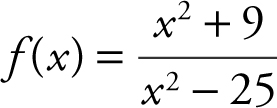 is concave upward or downward.
is concave upward or downward.
4 . Given f (x ) = x + sin x 0 ≤ x ≤ 2π , find all points of inflection of f .
5 . Show that the absolute minimum of 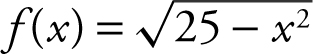 on [– 5, 5] is 0 and the absolute maximum is 5.
on [– 5, 5] is 0 and the absolute maximum is 5.
6 . Given the function f in Figure 8.6-1 , identify the points where:
(a) f ′ < 0 and f ″ > 0,
(b) f ′ < 0 and f ″ < 0,
(c) f ′ = 0,
(d) f ″ does not exist.
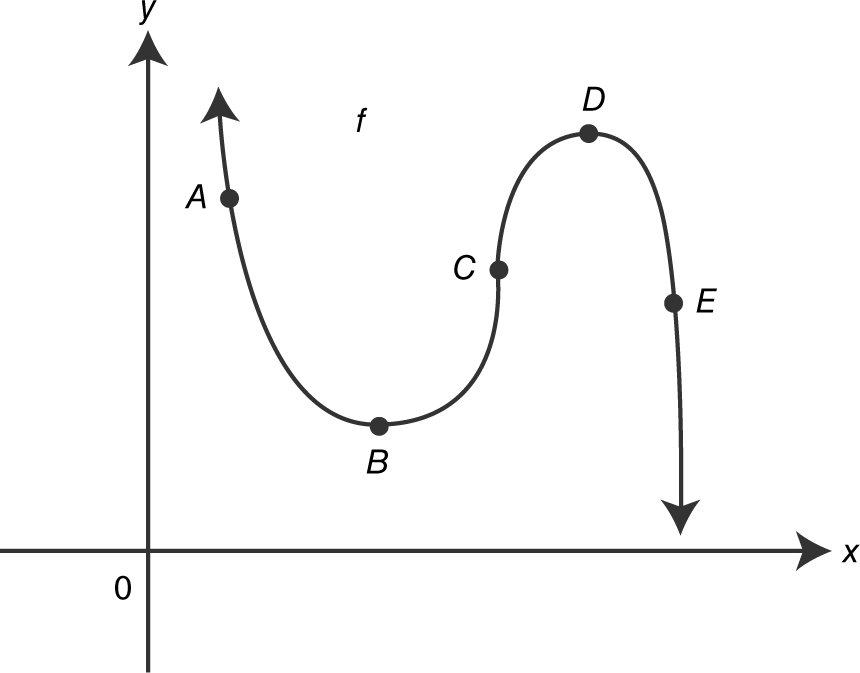
Figure 8.6-1
7 . Given the graph of f ″ in Figure 8.6-2 , determine the values of x at which the function f has a point of inflection.
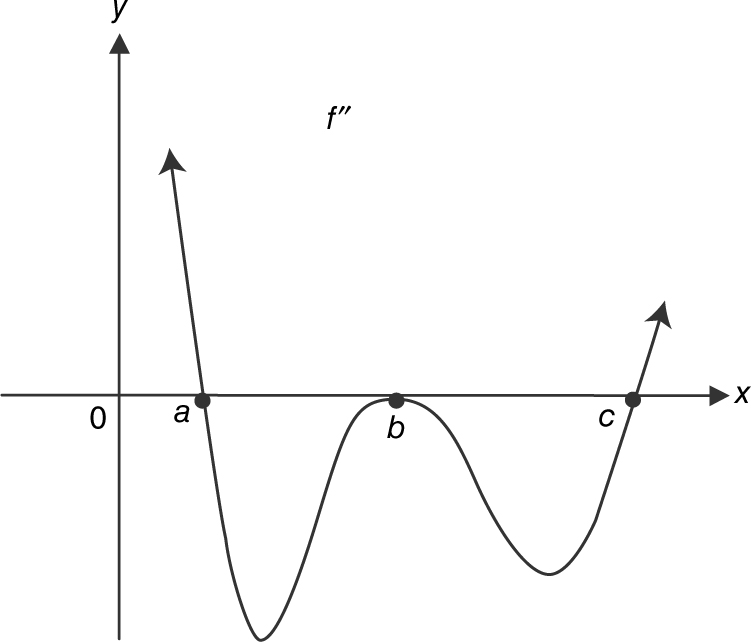
Figure 8.6-2
8 . If f ″(x ) = x 2 (x + 3)(x – 5), find the values of x at which the graph of f has a change of concavity.
9 . The graph of f ′ on [–3, 3] is shown in Figure 8.6-3 . Find the values of x on [–3, 3] such that (a) f is increasing and (b) f is concave downward.
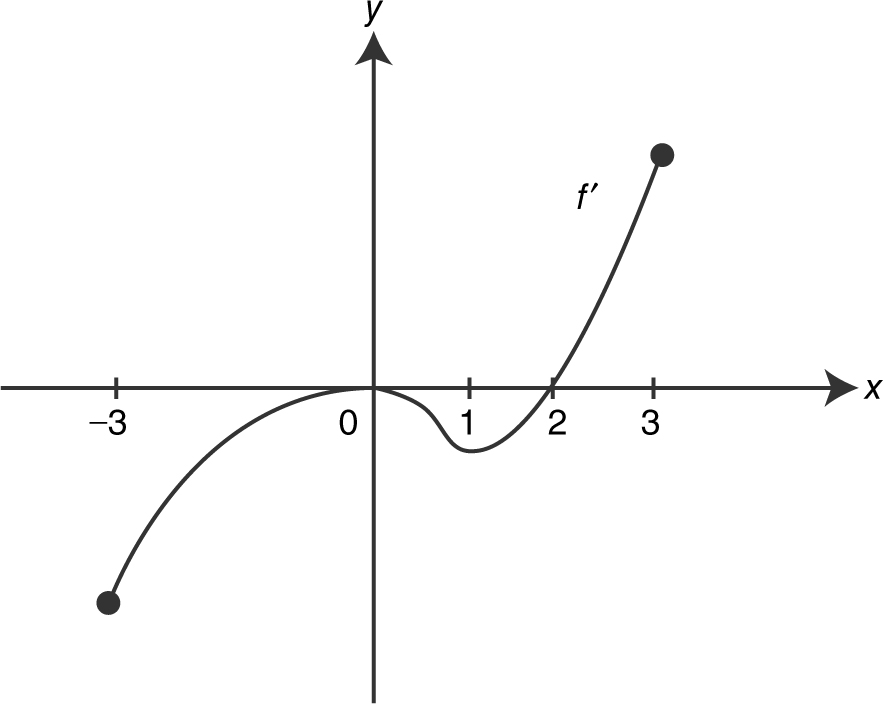
Figure 8.6-3
10 . The graph of f is shown in Figure 8.6-4 and f is twice differentiable. Which of the following has the largest value:
(a) f (–1)
(b) f ′(–1)
(c) f ″(–1)
(d) f (–1) and f ′(–1)
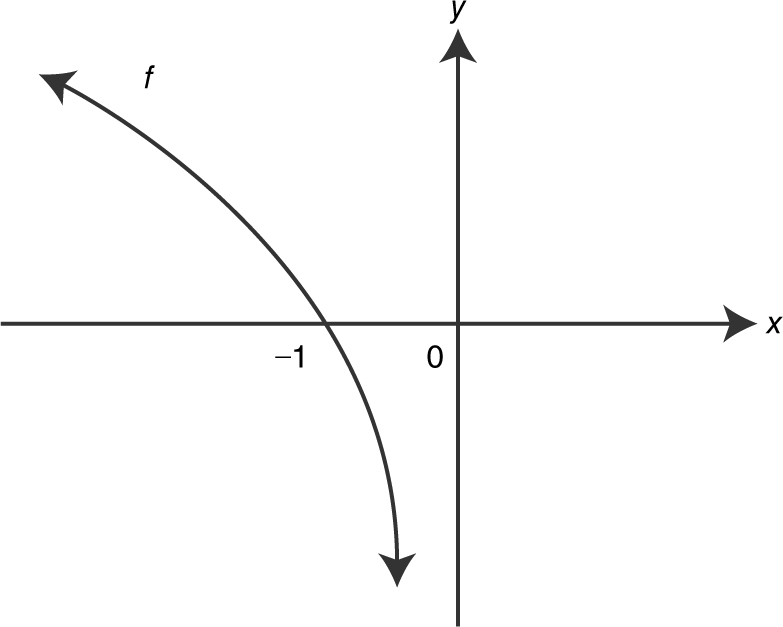
Figure 8.6-4
Sketch the graphs of the following functions indicating any relative and absolute extrema, points of inflection, intervals on which the function is increasing, decreasing, concave upward, or concave downward.
11 . f (x ) = x 4 – x 2
12 . 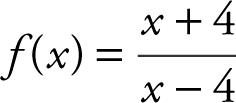
Part B Calculators are allowed.
13 . Given the graph of f ′ in Figure 8.6-5 , determine at which of the four values of x (x 1 , x 2 , x 3 , x 4 ) f has:
(a) the largest value,
(b) the smallest value,
(c) a point of inflection,
(d) and at which of the four values of x does f ″ have the largest value.
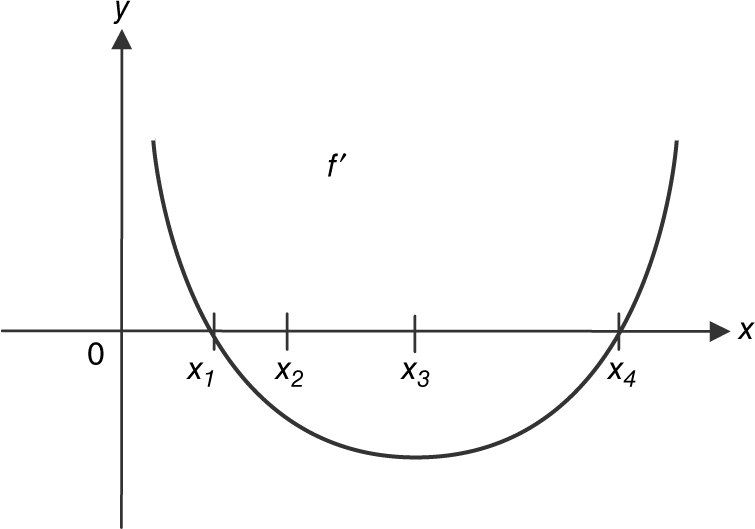
Figure 8.6-5
14 . Given the graph of f in Figure 8.6-6 , determine at which values of x is
(a) f ′(x ) = 0
(b) f ″(x ) = 0
(c) f ′ a decreasing function
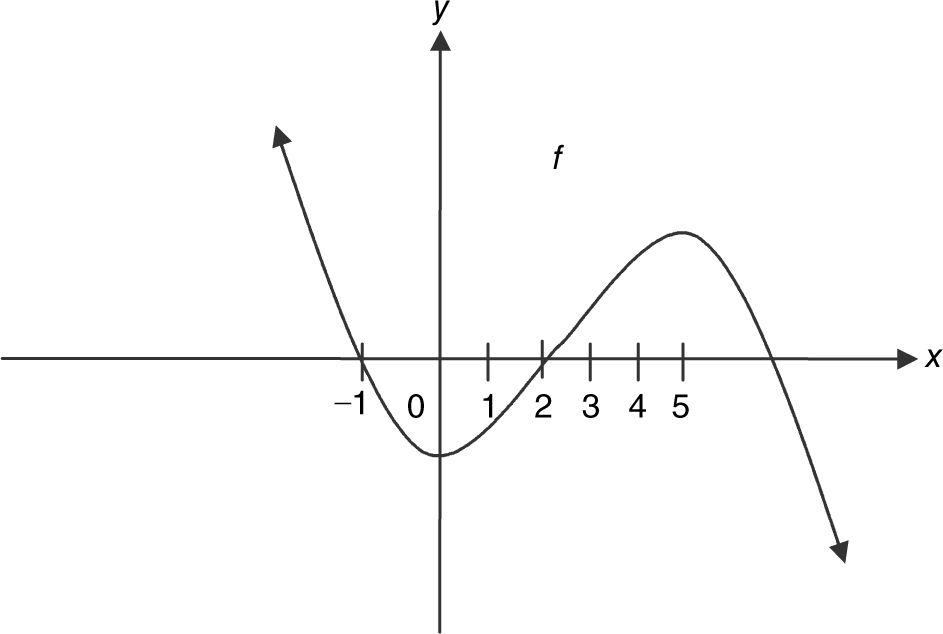
Figure 8.6-6
15 . A function f is continuous on the interval [–2, 5] with f (–2) = 10 and f (5) = 6 and the following properties:
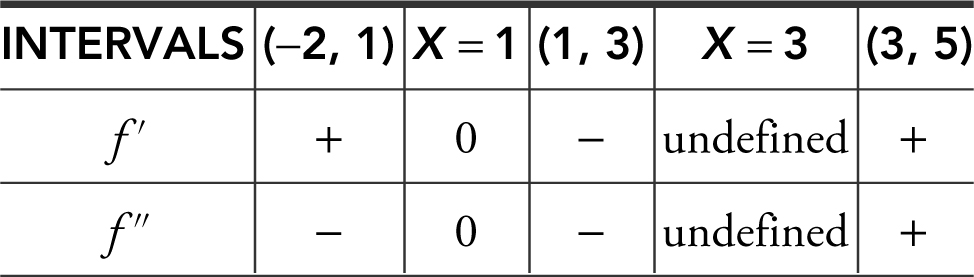
(a) Find the intervals on which f is increasing or decreasing.
(b) Find where f has its absolute extrema.
(c) Find where f has points of inflection.
(d) Find the intervals where f is concave upward or downward.
(e) Sketch a possible graph of f .
16 . Given the graph of f ′ in Figure 8.6-7 , find where the function f
(a) has its relative extrema.
(b) is increasing or decreasing.
(c) has its point(s) of inflection.
(d) is concave upward or downward.
(e) if f (0) = 1 and f (6) = 5, draw a sketch of f .
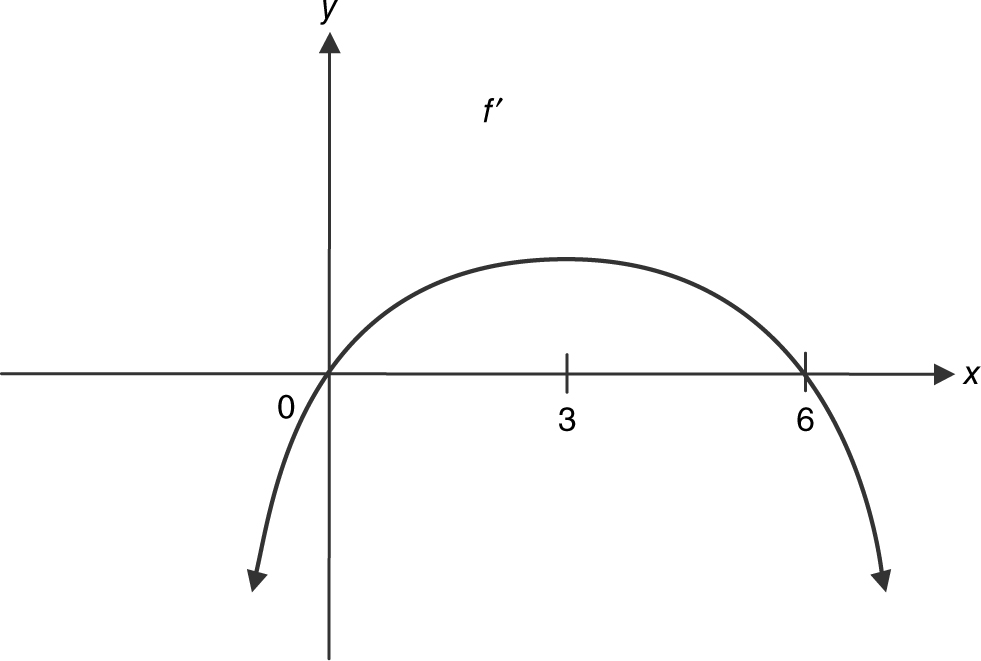
Figure 8.6-7
17 . If f (x ) = |x 2 – 6x – 7|, which of the following statements about f are true?
I. f has a relative maximum at x = 3.
II. f is differentiable at x = 7.
III. f has a point of inflection at x = –1.
18 . How many points of inflection does the graph of y = cos(x 2 ) have on the interval [–π , π ]?
Sketch the graphs of the following functions indicating any relative extrema, points of inflection, asymptotes, and intervals where the function is increasing, decreasing, concave upward, or concave downward.
19 . f (x ) = 3e – x 2 /2
20 . f (x ) = cos x sin2 x [0, 2π ]
8.7 Cumulative Review Problems
(Calculator) indicates that calculators are permitted.
21 . Find 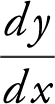 if (x 2 + y 2 )2 = 10xy .
if (x 2 + y 2 )2 = 10xy .
22 . Evaluate 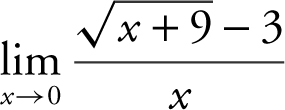
23 . Find 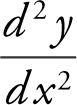 if y = cos(2x ) + 3x 2 – 1.
if y = cos(2x ) + 3x 2 – 1.
24 . (Calculator) Determine the value of k such that the function
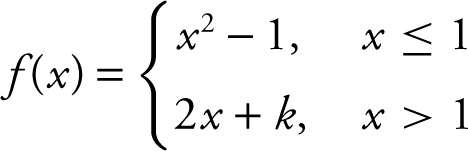 is continuous
is continuous
for all real numbers.
25 . A function f is continuous on the interval [–1, 4] with f (–1) = 0 and f (4) = 2 and the following properties:
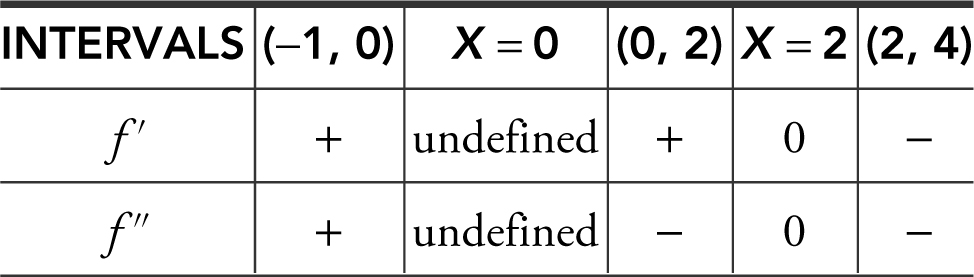
(a) Find the intervals on which f is increasing or decreasing.
(b) Find where f has its absolute extrema.
(c) Find where f has points of inflection.
(d) Find intervals on which f is concave upward or downward.
(e) Sketch a possible graph of f .
8.8 Solutions to Practice Problems
Part A—The use of a calculator is not allowed.
1 . Condition 1: Since f (x ) is a polynomial, it is continuous on [–1, 2].
Condition 2: Also, f (x ) is differentiable on (–1, 2) because f ′(x ) = 3x 2 – 2x – 2 is defined for all numbers in [–1, 2].
Condition 3: f (–1) = f (2) = 0. Thus, f (x ) satisfies the hypotheses of Rolle’s Theorem which means there exists a c in [–1, 2] such that f ′(c ) = 0. Set f ′(x ) = 3x 2 – 2x – 2 = 0. Solve 3x 2 – 2x – 2 = 0, using the quadratic formula and obtain 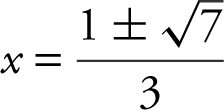 . Thus, x ≈ 1.215 or –0.549 and both values are in the interval (–1, 2). Therefore,
. Thus, x ≈ 1.215 or –0.549 and both values are in the interval (–1, 2). Therefore, 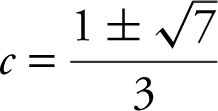 .
.
2 . Condition 1: f (x ) = ex is continuous on [0, 1].
Condition 2: f (x ) is differentiable on (0, 1) since f ′(x ) = ex is defined for all numbers in [0, 1].
Thus, there exists a number c in [0, 1] such that 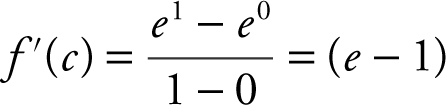 . Set f ′(x ) = e x = (e – 1). Thus, e x = (e – 1). Take ln of both sides. ln(e x ) = ln(e – 1) ⇒ x = ln(e – 1).
. Set f ′(x ) = e x = (e – 1). Thus, e x = (e – 1). Take ln of both sides. ln(e x ) = ln(e – 1) ⇒ x = ln(e – 1).
Thus, x ≈ 0.541 which is in the interval (0, 1). Therefore, c = ln(e – 1).
3 . 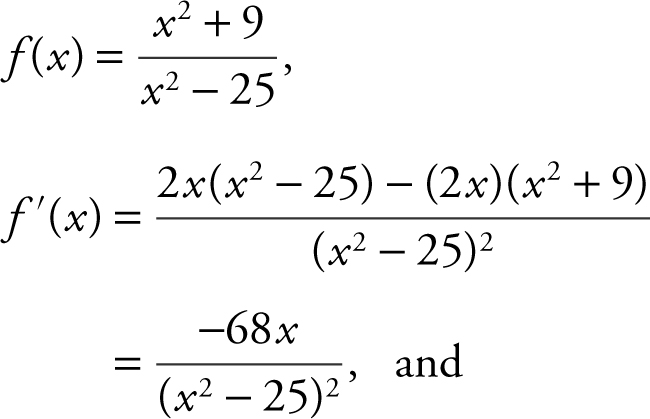
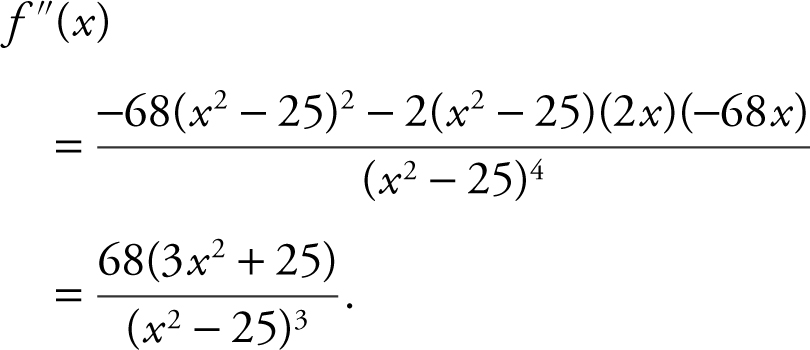
Set f ″ > 0. Since (3x 2 + 25) > 0, ⇒ (x 2 – 25)3 > 0 ⇒ x 2 – 25 > 0, x < –5 or x > 5. Thus, f (x ) is concave upward on (–∞, –5) and (5, ∞) and concave downward on (–5, 5).
4 . Step 1: f (x ) = x + sin x ,
f ′(x ) = 1 + cos x ,
f ″ = – sin x .
Step 2: Set f ″(x ) = 0 ⇒ – sin x = 0 or
x = 0, π , 2π .
Step 3: Check intervals.
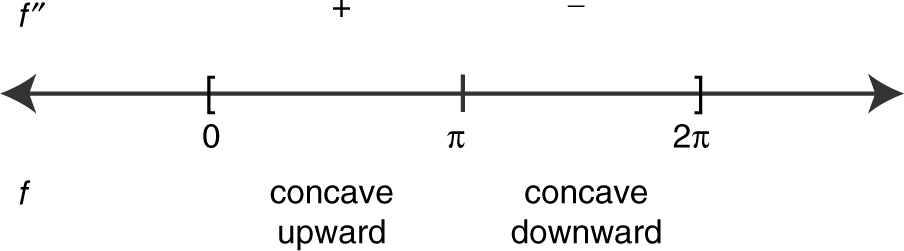
Step 4: Check for tangent line: At x = π , f ′(x ) = 1 + (–1) ⇒ 0 there is a
tangent line at x = π .
Step 5: Thus, (π , π ) is a point of inflection.
5 . Step 1: Rewrite f (x ) as
f (x ) = (25 – x 2 )1/2 .
Step 2: 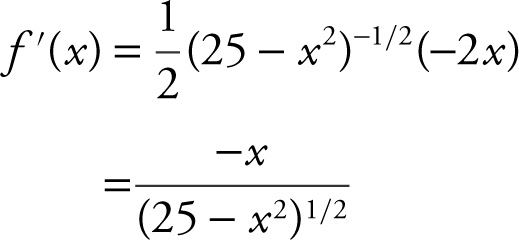
Step 3: Find critical numbers. f ′(x ) = 0; at x = 0; and f ′(x ) is undefined at x = ±5.
Step 4: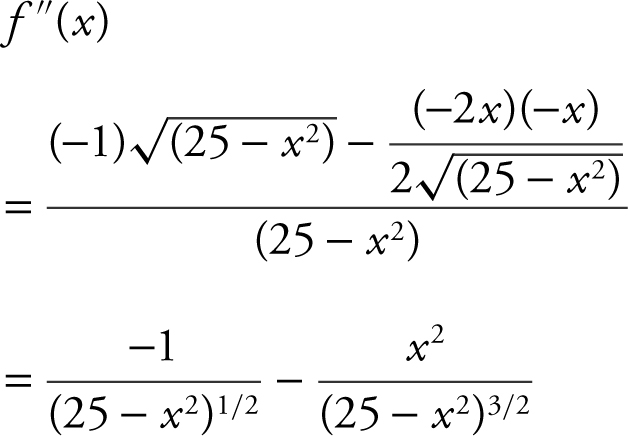
f ′(0) = 0 and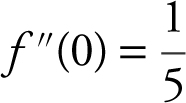
(and f (0) = 5) ⇒ (0, 5) is a relative maximum. Since f (x ) is continuous on [–5, 5], f (x ) has both a maximum and a minimum value on [–5, 5] by the Extreme Value Theorem. And since the point (0,5) is the only relative extremum, it is an absolute extremum. Thus, (0,5) is an absolute maximum point and 5 is the maximum value. Now we check the endpoints, f (–5) = 0 and f (5) = 0. Therefore, (–5, 0) and (5, 0) are the lowest points for fon [–5, 5]. Thus, 0 is the absolute minimum value.
6 . (a) Point A f ′ < 0 ⇒ decreasing and f ″ > 0 ⇒ concave upward.
(b) Point E f ′ < 0 ⇒ decreasing and f ″ < 0 ⇒ concave downward.
(c) Points B and D f ′ = 0 ⇒ horizontal tangent.
(d) Point C f ″ does not exist ⇒ vertical tangent.
7 . A change in concavity ⇒ a point of inflection. At x = a , there is a change of concavity; f ″ goes from positive to negative ⇒ concavity changes from upward to downward. At x = c , there is a change of concavity; f ″ goes from negative to positive ⇒ concavity changes from downward to upward. Therefore, f has two points of inflection, one at x = a and the other at x = c .
8 . Set f ″(x ) = 0. Thus, x 2 (x + 3)(x – 5) = 0 ⇒ x = 0, x = –3 or x = 5. (See Figure 8.8-1 .)
Thus, f has a change of concavity at x = –3 and at x = 5.
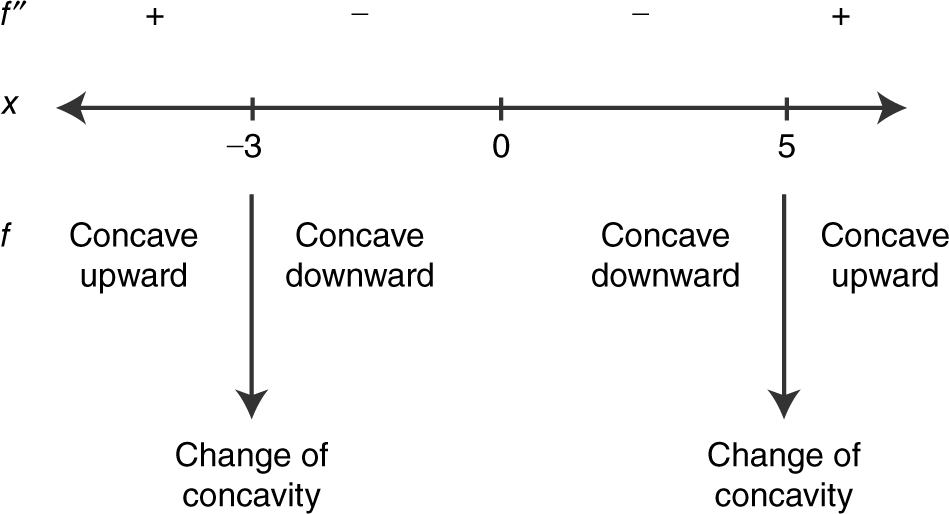
Figure 8.8-1
9 . (See Figure 8.8-2 .)
Thus, f is increasing on [2, 3] and concave downward on (0, 1).
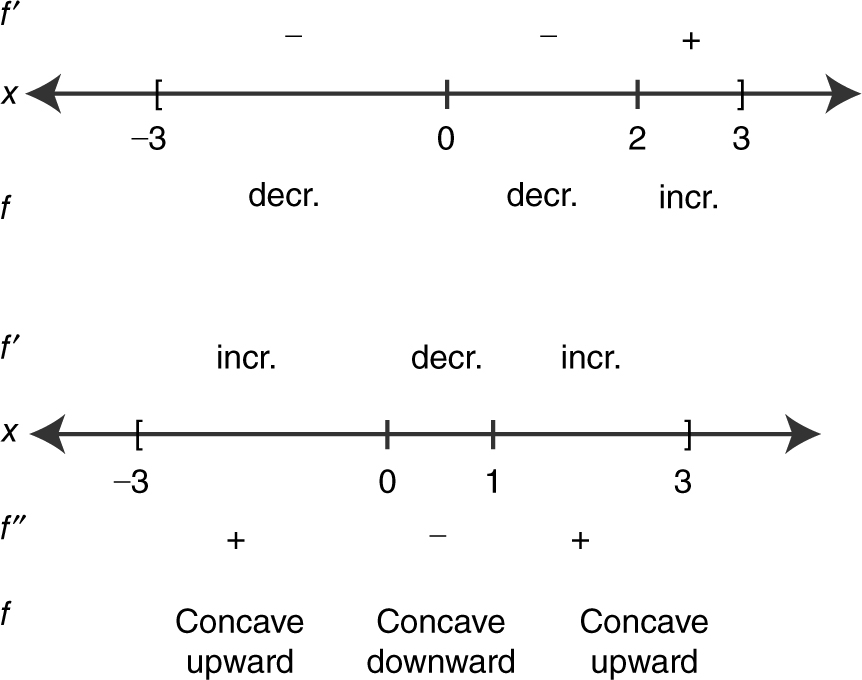
Figure 8.8-2
10 . The correct answer is (A).
f (–1) = 0; f ′(0) < 0 since f is decreasing and f ″(–1) < 0 since f is concave downward. Thus, f (–1) has the largest value.
11 . Step 1: Domain: all real numbers.
Step 2: Symmetry: Even function (f (x ) = f (– x )); symmetrical with respect to the y -axis.
Step 3: f ′(x ) = 4x 3 – 2x and f ″(x ) = 12x 2 – 2.
Step 4: Critical numbers: f ′(x ) is defined for all real numbers. Set f ′(x ) = 4x 3 – 2x = 0 ⇒ 2x (2x 2 – 1) = 0 ⇒ x = 0 or x = ±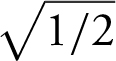 . Possible points of inflection: f ″(x ) is defined for all real numbers. Set f ″(x ) = 12x 2 – 2 = 0
. Possible points of inflection: f ″(x ) is defined for all real numbers. Set f ″(x ) = 12x 2 – 2 = 0
x = ±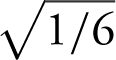 .
.
Step 5: Determine intervals:
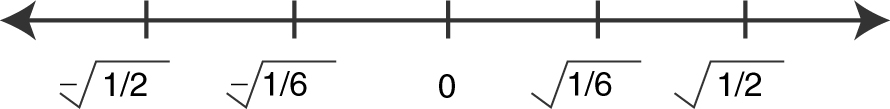
Intervals are: 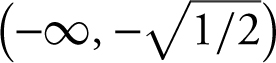
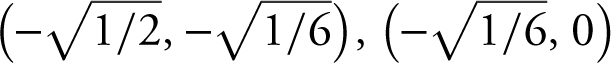 ,
,
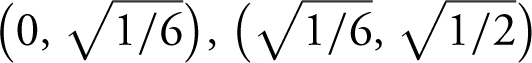 , and
, and
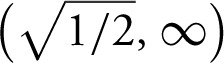 .
.
Since f ′(x ) is symmetrical with respect to the y -axis, you only need to examine half of the intervals.
Step 6: Set up a table (Table 8.8-1 ). The function has an absolute minimum value of (–1/4) and no absolute maximum value.
Table 8.8-1

Step 7: Sketch the graph. (See Figure 8.8-3 .)
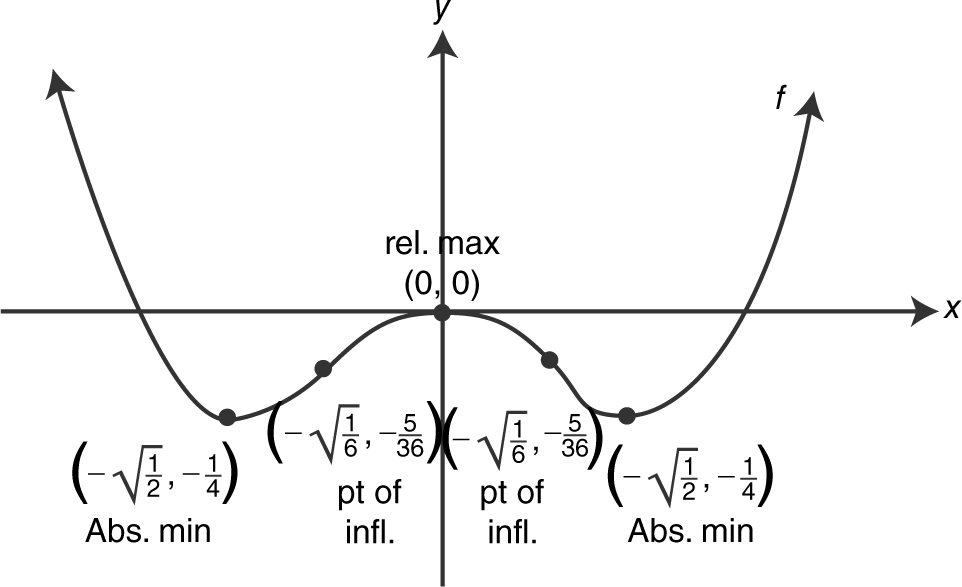
Figure 8.8-3
12 . Step 1: Domain: all real numbers x ≠ 4.
Step 2: Symmetry: none.
Step 3: Find f ′ and f ″.
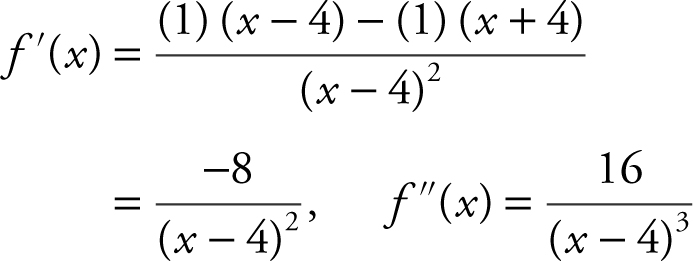
Step 4: Critical numbers: f ′(x ) ≠ 0 and f ′(x ) is undefined at x = 4.
Step 5: Determine intervals.

Intervals are (–∞, 4) and (4, ∞).
Step 6: Set up table as below:
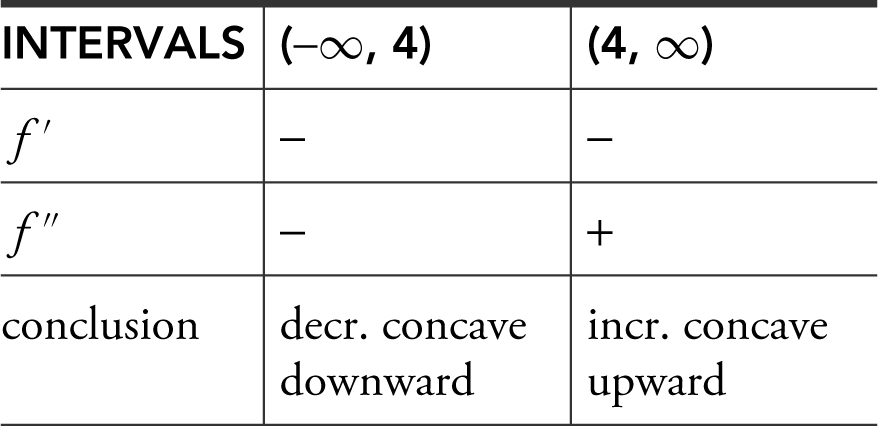
Step 7: Horizontal asymptote:
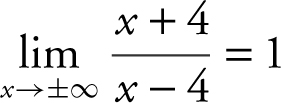 . Thus, y = 1 is a horizontal asymptote. Vertical asymptote:
. Thus, y = 1 is a horizontal asymptote. Vertical asymptote:
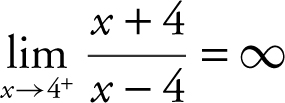 and
and
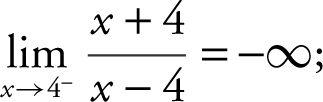 ; Thus, x = 4 is a vertical asymptote.
; Thus, x = 4 is a vertical asymptote.
Step 8: x -intercept: Set f ′(x ) = 0 ⇒ x + 4 = 0; x = –4. y -intercept: Set x = 0 ⇒ f (x ) = –1.
Step 9: Sketch the graph. (See Figure 8.8-4 .)
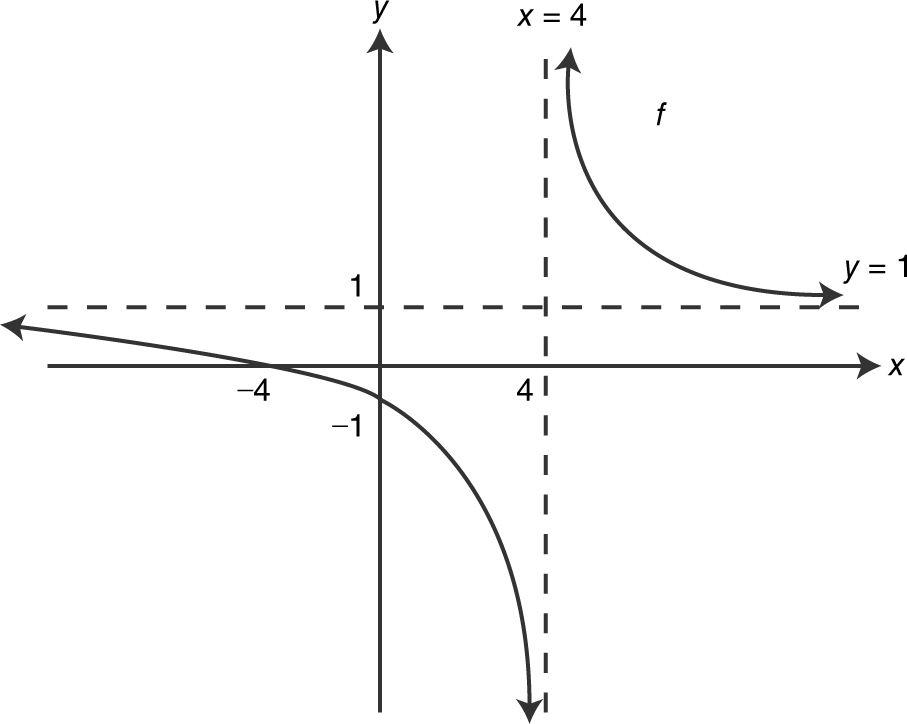
Figure 8.8-4
13 . (a)

The function f has the largest value (of the four choices) at x = x 1 . (See Figure 8.8-5 .)
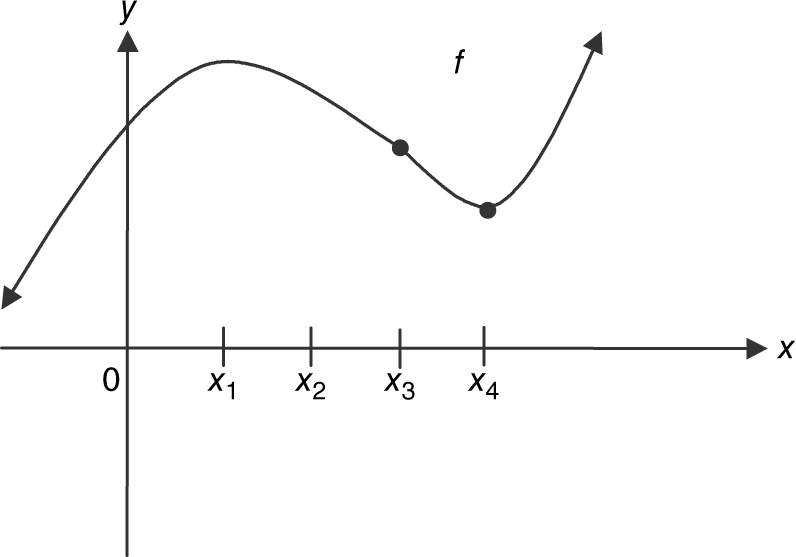
Figure 8.8-5
(b) And f has the smallest value at x = x 4 .
(c)
A change of concavity occurs at x = x 3 , and f ′(x 3 ) exists which implies there is a tangent to f at x = x 3 . Thus, at x = x 3 , f has a point of inflection.
(d) The function f ″ represents the slope of the tangent to f ′. The slope of the tangent to f ′ is the largest at x = x 4 .
14 . (a) Since f ′(x ) represents the slope of the tangent, f ′(x ) = 0 at x = 0, and x = 5.
(b) At x = 2, f has a point of inflection which implies that if f ″(x ) exists, f ″(x ) = 0. Since f ′(x ) is differentiable for all numbers in the domain, f ″(x ) exists, and f ″(x ) = 0 at x = 2.
(c) Since the function f is concave downward on (2, ∞), f ″ < 0 on (2, ∞) which implies f ′ is decreasing on (2, ∞).
15 . (a) The function f is increasing on the intervals (–2, 1) and (3, 5) and decreasing on (1, 3).
(b) The absolute maximum occurs at x = 1, since it is a relative maximum, f (1) > f (–2) and f (5) < f (–2). Similarly, the absolute minimum occurs at x = 3, since it is a relative minimum, and f (3) < f (5) < f (–2).
(c) No point of inflection. (Note that at x = 3, f has a cusp.)
Note: Some textbooks define a point of inflection as a point where the concavity changes and do not require the existence of a tangent. In that case, at x = 3, f has a point of inflection.
(d) Concave upward on (3, 5) and concave downward on (–2, 3).
(e) A possible graph is shown in Figure 8.8-6 .
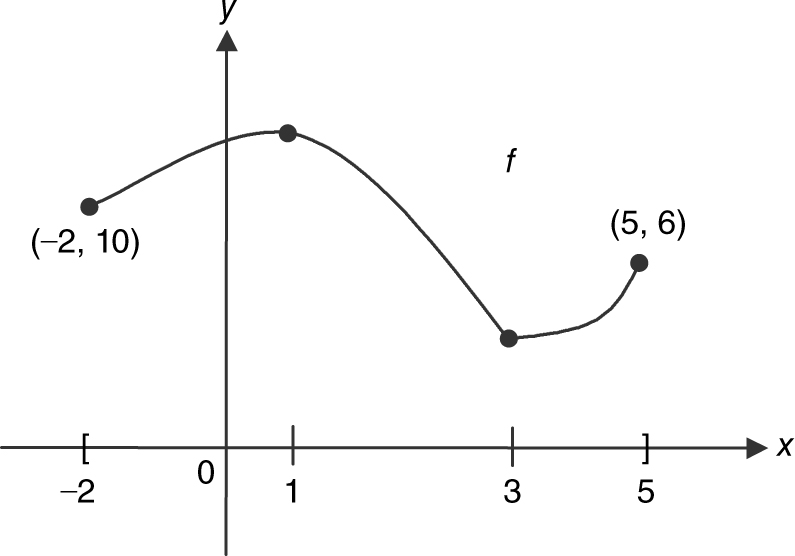
Figure 8.8-6
16 . (a)
The function f has its relative minimum at x = 0 and its relative maximum at x = 6.
(b) The function f is increasing on [0, 6] and decreasing on (– ∞, 0] and [6, ∞).
(c)
Since f ′(3) exists and a change of concavity occurs at x = 3, f has a point of inflection at x = 3.
(d) Concave upward on (–∞, 3) and downward on (3, ∞).
(e) Sketch a graph. (See Figure 8.8-7 .)
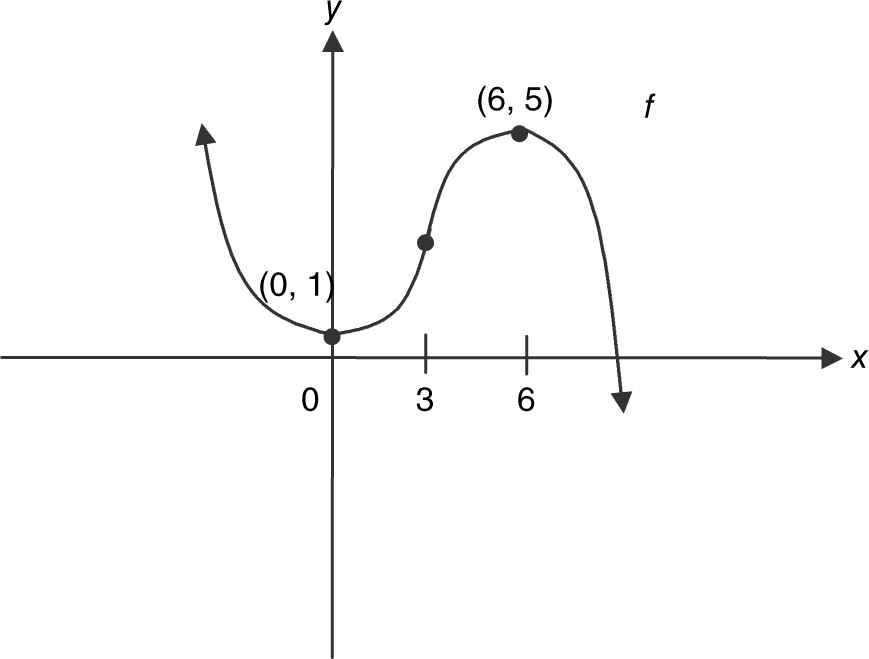
Figure 8.8-7
17 . (See Figure 8.8-8 .)
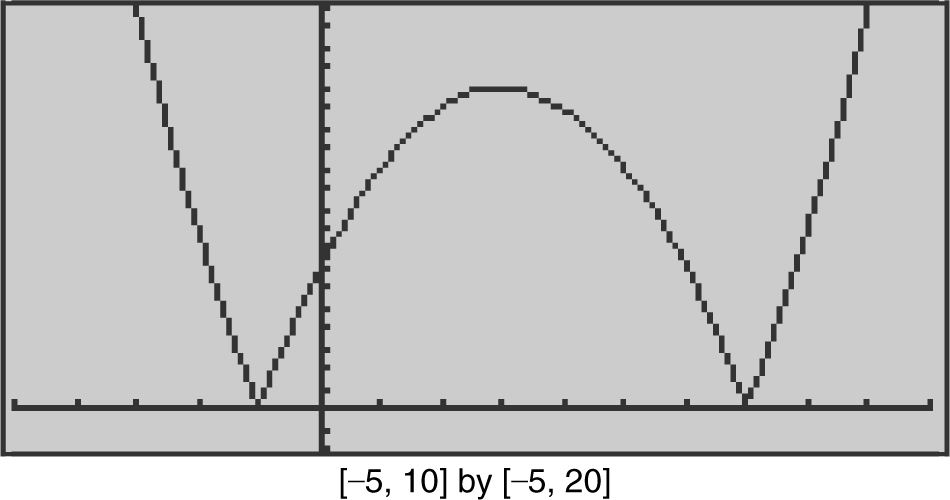
Figure 8.8-8
The graph of f indicates that a relative maximum occurs at x = 3, f is not differentiable at x = 7, since there is a cusp at x = 7 and f does not have a point of inflection at x = –1, since there is no tangent line at x = –1. Thus, only statement I is true.
18 . (See Figure 8.8-9 .)
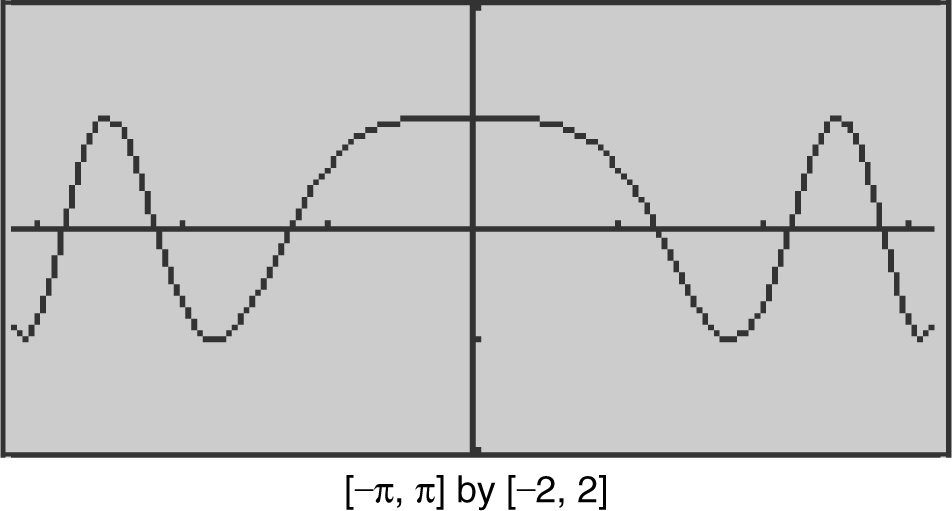
Figure 8.8-9
Enter y 1 = cos(x 2 )
Using the [Inflection ] function of your calculator, you obtain three points of inflection on [0, π ]. The points of inflection occur at x = 1.35521, 2.1945, and 2.81373. Since y 1 = cos(x 2 ) is an even function, there is a total of 6 points of inflection on [–π , π ]. An alternate solution is to enter 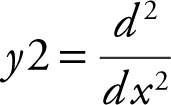 . (y 1 (x ), x , 2).
. (y 1 (x ), x , 2).
The graph of y 2 indicates that there are 6 zeros on [–π , π ].
19 . Enter y 1 = 3 ∗ e ∧ (–x ∧ 2/2). Note that the graph has a symmetry about the y -axis. Using the functions of the calculator, you will find:
(a) a relative maximum point at (0, 3), which is also the absolute maximum point;
(b) points of inflection at (–1, 1.819) and (1, 1.819);
(c) y = 0 (the x -axis) a horizontal asymptote;
(d) y 1 increasing on (–∞, 0] and decreasing on [0, ∞); and
(e) y 1 concave upward on (–∞, –1) and (1, ∞) and concave downward on (–1, 1). (See Figure 8.8-10 .)
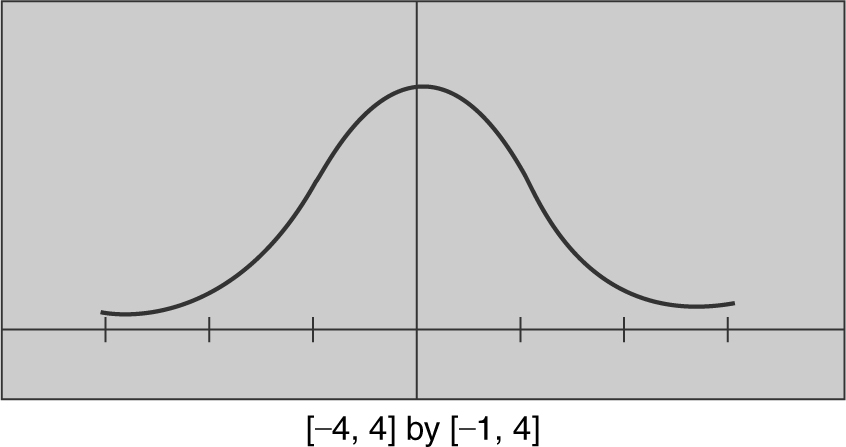
Figure 8.8-10
20 . (See Figure 8.8-11 .) Enter y 1 = cos(x ) ∗ (sin(x )) ∧ 2. A fundamental domain of y 1 is [0, 2 π ]. Using the functions of the calculator, you will find:
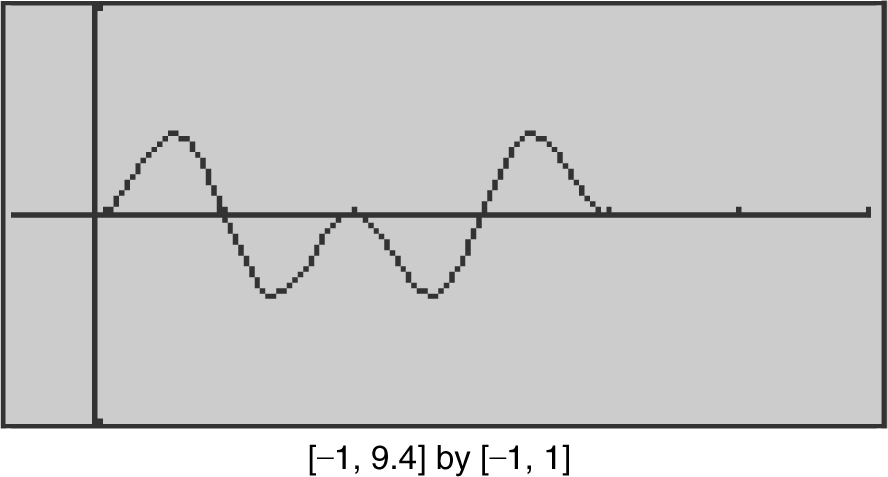
Figure 8.8-11
(a) relative maximum points at (0.955, 0.385), (π , 0), and (5.328, 0.385), and relative minimum points at (2.186, – 0.385) and (4.097, – 0.385);
(b) points of inflection at (0.491, 0.196), 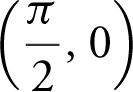 , (2.651, – 0.196), (3.632, – 0.196),
, (2.651, – 0.196), (3.632, – 0.196), 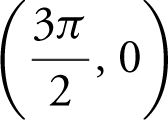 , and (5.792, 0.196);
, and (5.792, 0.196);
(c) no asymptote;
(d) function is increasing on intervals (0, 0.955), (2.186, π ), and (4.097, 5.328), and decreasing on intervals (0.955, 2.186), (π , 4.097), and (5.328, 2π );
(e) function is concave upward on intervals (0, 0.491), 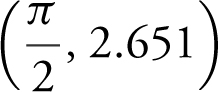
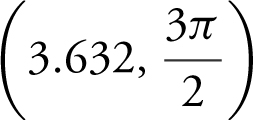 , and (5.792, 2π ), and concave downward on the intervals
, and (5.792, 2π ), and concave downward on the intervals 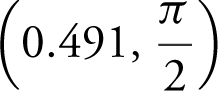 , (2.651,3.632), and
, (2.651,3.632), and 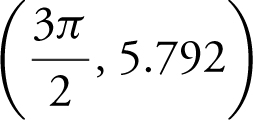 .
.
8.9 Solutions to Cumulative Review Problems
21 . 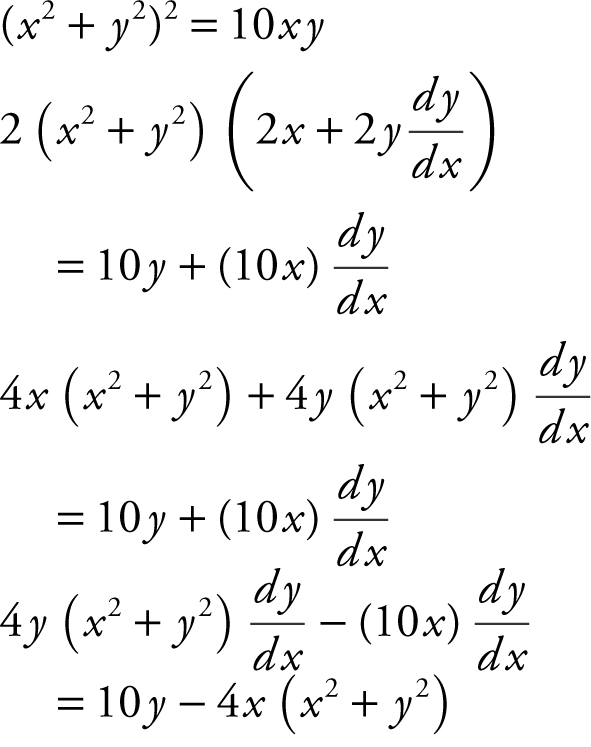
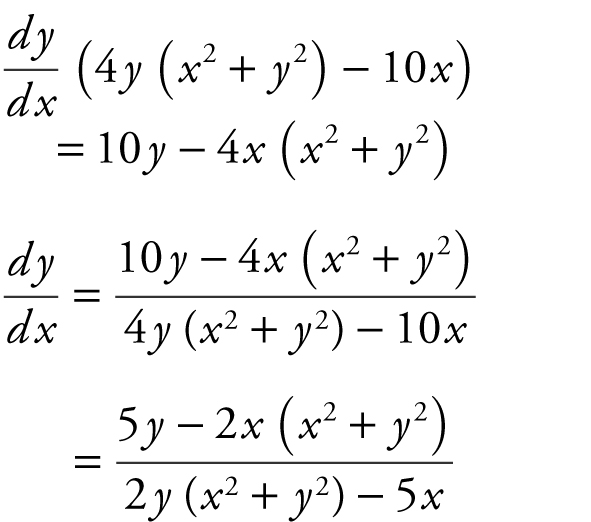
22 . Substituting x = 0 in the expression 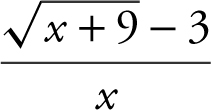 leads to
leads to ![]() , ana indeterminant form. Apply L’Hôpital’s Rule and you have
, ana indeterminant form. Apply L’Hôpital’s Rule and you have 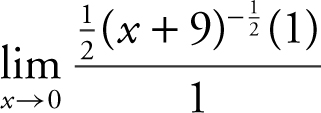 or
or 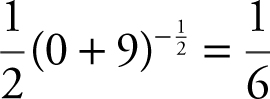 . Alternatively,
. Alternatively, 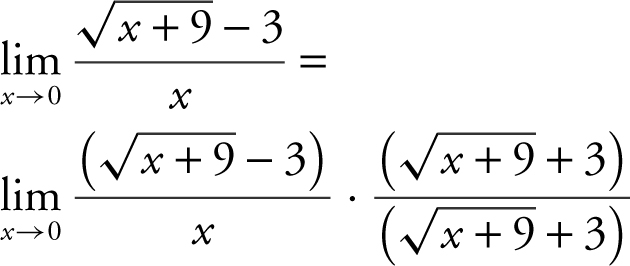
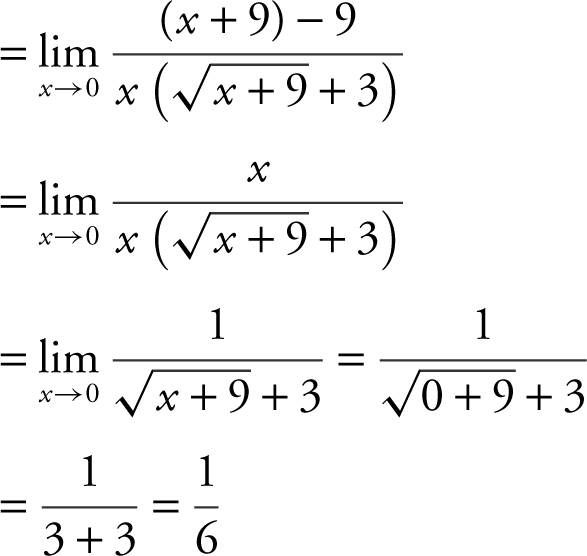
23 . y = cos(2x ) + 3x 2 – 1 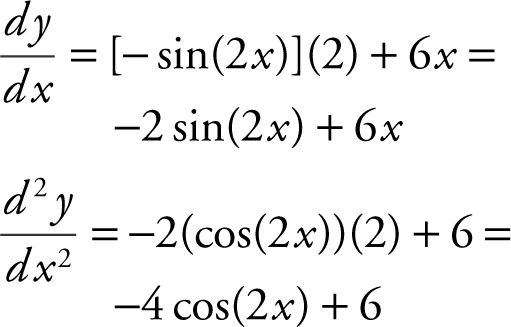
24 . (Calculator) The function f is continuous everywhere for all values of k except possibly at x = 1. Checking with the three conditions of continuity at x = 1:
(1) f (1) = (1)2 – 1 = 0
(2) 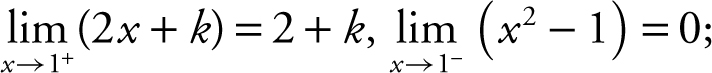 thus, 2 + k 0 ⇒ k = – 2. Since
thus, 2 + k 0 ⇒ k = – 2. Since 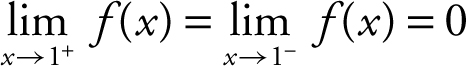 , therefore,
, therefore, 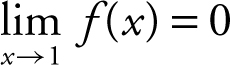 .
.
(2) 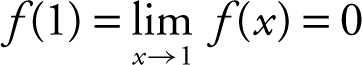 . Thus, k = –2.
. Thus, k = –2.
25 . (a) Since f ′ > 0 on (-1, 0) and (0, 2), the function f is increasing on the intervals [-1, 0] and [0, 2]. Since f ′ < 0 on (2, 4), f is decreasing on [2, 4].
(b) The absolute maximum occurs at x = 2, since it is a relative maximum and it is the only relative extremum on (–1, 4). The absolute minimum occurs at x = –1, since f (–1) < f (4) and the function has no relative minimum on [–1, 4].
(c) A change of concavity occurs at x = 0. However, f ′(0) is undefined, which implies f may or may not have a tangent at x = 0. Thus, f may or may not have a point of inflection at x = 0.
(d) Concave upward on (–1, 0) and concave downward on (0, 4).
(e) A possible graph is shown in Figure 8.9-1 .
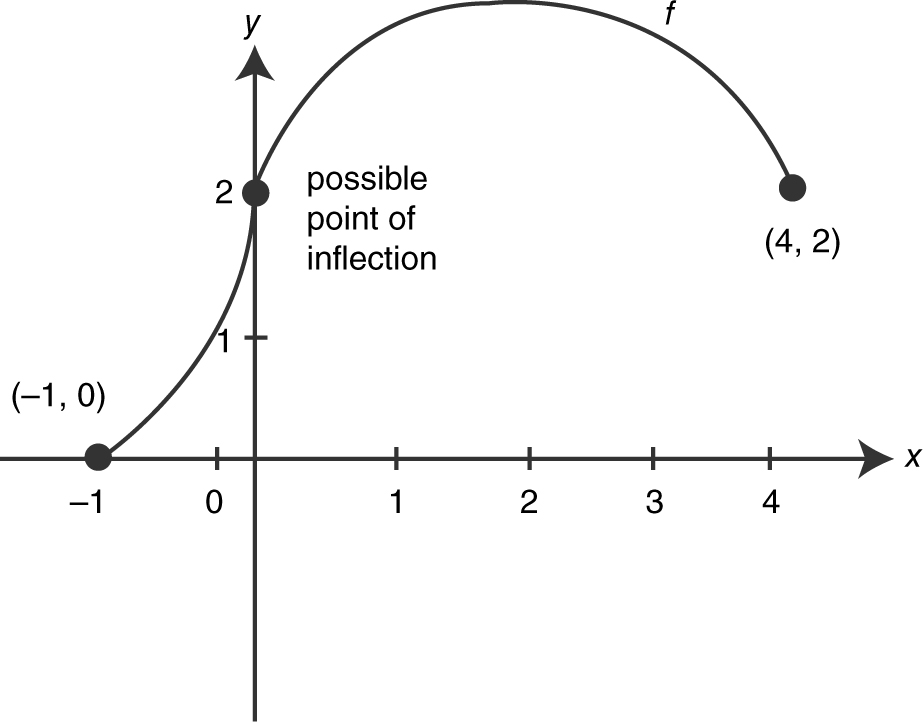
Figure 8.9-1