Calculus AB and Calculus BC

CHAPTER 3 Differentiation

D. DIFFERENTIABILITY AND CONTINUITY

If a function f has a derivative at x = c, then f is continuous at x = c.

This statement is an immediate consequence of the definition of the derivative of f ′(c) in the form

If f ′(c) exists, then it follows that which guarantees that f is continuous at x = c.

If f is differentiable at c, its graph cannot have a hole or jump at c, nor can x = c be a vertical asymptote of the graph. The tangent to the graph of f cannot be vertical at x = c; there cannot be a corner or cusp at x = c.

Each of the “prohibitions” in the preceding paragraph (each “cannot”) tells how a function may fail to have a derivative at c. These cases are illustrated in Figures N3–2 (a) through (f).

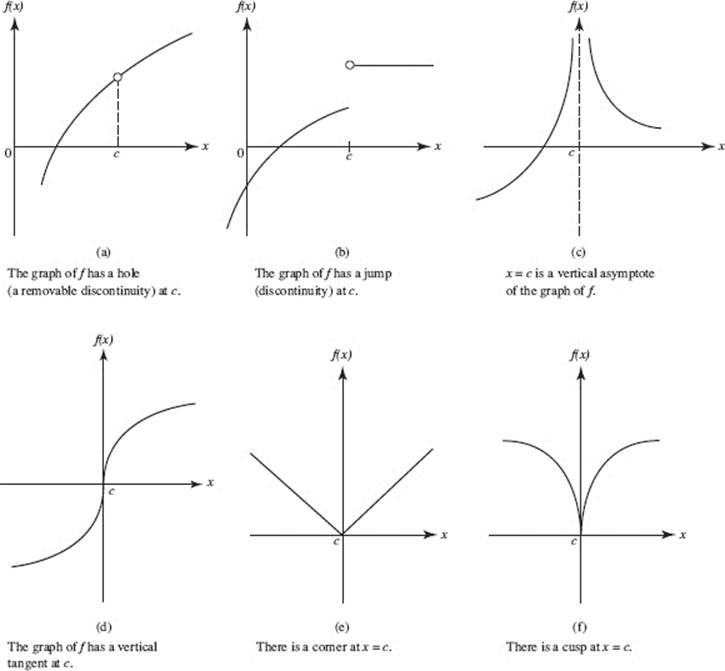
FIGURE N3–2

The graph in (e) is for the absolute function, f (x) = |x|. Since f ′(x) = −1 for all negative x but f ′(x) = + 1 for all positive x, f ′(0) does not exist.

We may conclude from the preceding discussion that, although differentiability implies continuity, the converse is false. The functions in (d), (e), and (f) in Figure N3–2 are all continuous at x = 0, but not one of them is differentiable at the origin.