Calculus AB and Calculus BC
CHAPTER 4 Applications of Differential Calculus
K. MOTION ALONG A CURVE: VELOCITY AND ACCELERATION VECTORS
If a point P moves along a curve defined parametrically by P(t) = (x(t), y(t)), where t represents time, then the vector from the origin to P is called the position vector, with x as its horizontal component and y as its vertical component. The set of position vectors for all values of t in the domain common to x(t) and y(t) is called vector function.
A vector may be symbolized either by a boldface letter (R) or an italic letter with an arrow written over it ![]() The position vector, then, may be written as
The position vector, then, may be written as ![]() or as
or as ![]() In print the boldface notation is clearer, and will be used in this book; when writing by hand, the arrow notation is simpler.
In print the boldface notation is clearer, and will be used in this book; when writing by hand, the arrow notation is simpler.
The velocity vector is the derivative of the vector function (the position vector):
![]()
Alternative notations for ![]() are vx and vy, respectively; these are the components of v in the horizontal and vertical directions, respectively. The slope of v is
are vx and vy, respectively; these are the components of v in the horizontal and vertical directions, respectively. The slope of v is

which is the slope of the curve; the magnitude of v is the vector’s length:
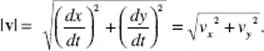
BC ONLY
Thus, if the vector v is drawn initiating at P, it will be tangent to the curve at P and its magnitude will be the speed of the particle at P.
The acceleration vector a is ![]() and can be obtained by a second differentiation of the components of R. Thus
and can be obtained by a second differentiation of the components of R. Thus
![]()
and its magnitude is the vector’s length:
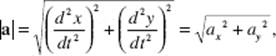
where we have used ax and ay for ![]() respectively.
respectively.
Examples 28 and 29 are BC ONLY.
EXAMPLE 28
A particle moves according to the equations x = 3 cost, y = 2 sin t.
(a) Find a single equation in x and y for the path of the particle and sketch the curve.
(b) Find the velocity and acceleration vectors at any time t, and show that a = −R at all times.
(c) Find R, v, and a when (1) ![]() (2) t2 = π, and draw them on the sketch.
(2) t2 = π, and draw them on the sketch.
(d) Find the speed of the particle and the magnitude of its acceleration at each instant in (c).
(e) When is the speed a maximum? A minimum?
SOLUTIONS:
(a) Since ![]() therefore
therefore
![]()
and the particle moves in a counterclockwise direction along an ellipse, starting, when t = 0, at (3,0) and returning to this point when t = 2π.
(b) We have

The acceleration, then, is always directed toward the center of the ellipse.
(c) At ![]()
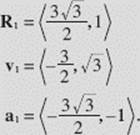
At t2 = π,
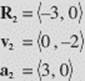
The curve, and v and a at t1 and t2, are sketched in Figure N4–18, below.
|
(d) At |
At t2 = π, |
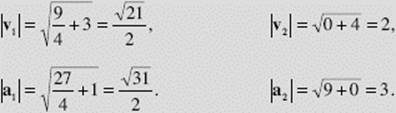
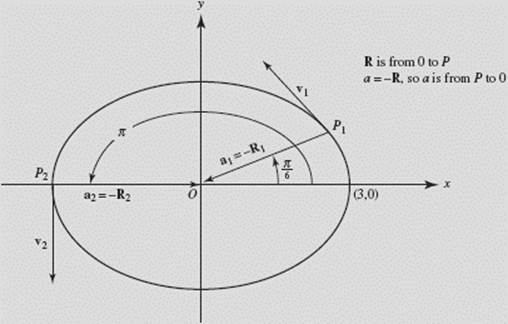
FIGURE N4–18
(e) For the speed |v| at any time t
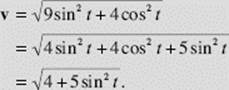
We see immediately that the speed is a maximum when ![]() and a minimum when t = 0 or π. The particle goes fastest at the ends of the minor axis and most slowly at the ends of the major axis. Generally one can determine maximum or minimum speed by finding
and a minimum when t = 0 or π. The particle goes fastest at the ends of the minor axis and most slowly at the ends of the major axis. Generally one can determine maximum or minimum speed by finding ![]() setting it equal to zero, and applying the usual tests to sort out values of t that yield maximum or minimum speeds.
setting it equal to zero, and applying the usual tests to sort out values of t that yield maximum or minimum speeds.
EXAMPLE 29
A particle moves along the parabola y = x2 − x with constant speed ![]() Find v at (2,2).
Find v at (2,2).
SOLUTION: Since
![]()
and
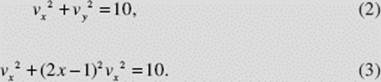
Relation (3) holds at all times; specifically, at (2, 2), ![]() so that vx = ±1. From (1), then, we see that vy = ±3. Therefore v at (2, 2) is either
so that vx = ±1. From (1), then, we see that vy = ±3. Therefore v at (2, 2) is either ![]() The former corresponds to counterclockwise motion along the parabola, as shown in Figure N4–19a; the latter to clockwise motion, indicated in Figure N4–19b.
The former corresponds to counterclockwise motion along the parabola, as shown in Figure N4–19a; the latter to clockwise motion, indicated in Figure N4–19b.
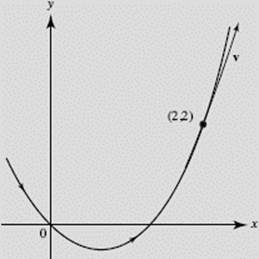
FIGURE N4–19a
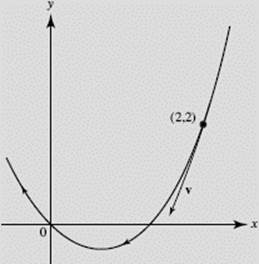
FIGURE N4–19b