Calculus AB and Calculus BC
CHAPTER 5 Antidifferentiation
B. BASIC FORMULAS
Familiarity with the following fundamental integration formulas is essential.
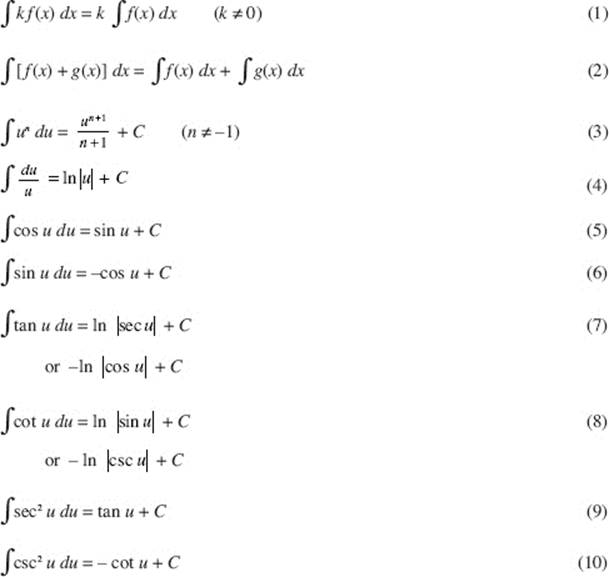
All the references in the following set of examples are to the preceding basic formulas. In all of these, whenever u is a function of x, we define du to be u ′(x) dx; when u is a function of t, we define du to be u ′(t) dt; and so on.
EXAMPLE 1
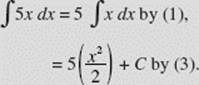
EXAMPLE 2
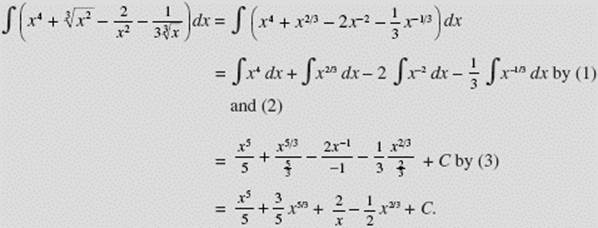
EXAMPLE 3
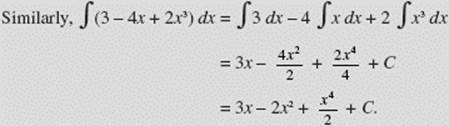
EXAMPLE 4
is integrated most efficiently by using formula (3) with u = 1 − 3x and du = u ′(x)dx = −3 dx.
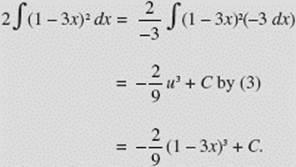
EXAMPLE 5
where u = 2x3 − 1 and du = u ′(x) dx = 6x2 dx; this, by formula (3), equals
EXAMPLE 6
du, where u = 1 − x and du = −1 dx; this, by formula (3) yields 
EXAMPLE 7
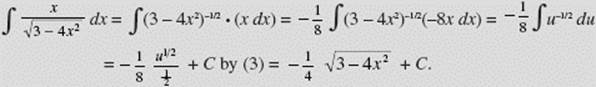
EXAMPLE 8
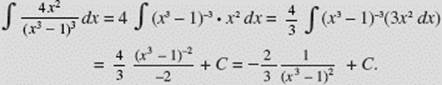
EXAMPLE 9
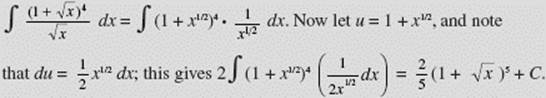
EXAMPLE 10
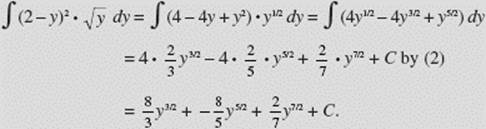
EXAMPLE 11
EXAMPLE 12
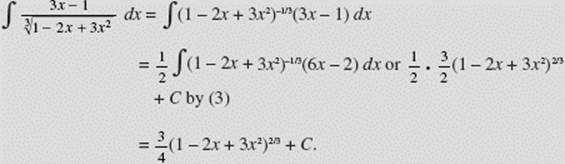
EXAMPLE 13
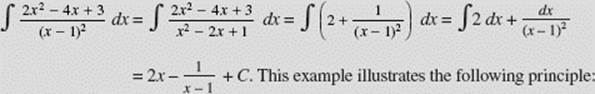
If the degree of the numerator of a rational function is not less than that of the denominator, divide until a remainder of lower degree is obtained.
EXAMPLE 14
EXAMPLE 15
EXAMPLE 16
with u = 5 + 2 sin x. The absolute-value sign is not necessary here since (5 + 2 sin x) > 0 for all x.
EXAMPLE 17
EXAMPLE 18
(by long division) = −x − ln |1 − x| + C.
EXAMPLE 19
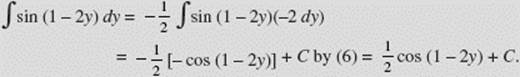
EXAMPLE 20
EXAMPLE 21
EXAMPLE 22
EXAMPLE 23
EXAMPLE 24
EXAMPLE 25
+ C by (3) with u = tan t and du = u ′(t) dt = sec2 t dt.
EXAMPLE 26
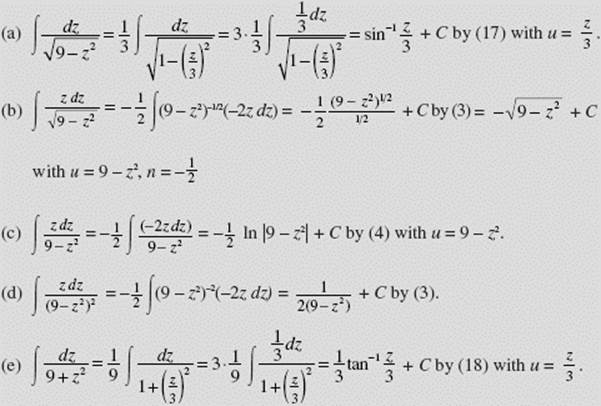
EXAMPLE 27
by (4)
with u = 1 + 2
and 
EXAMPLE 28
with u = cos x; 
cos 2x + C by (6), where we use the trigonometric identity sin 2x = 2 sin x cos x.
EXAMPLE 29
EXAMPLE 30
using the trigonometric identity 
EXAMPLE 31
EXAMPLE 32
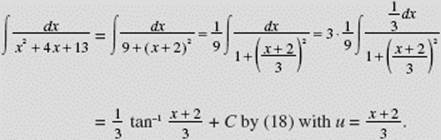
EXAMPLE 33
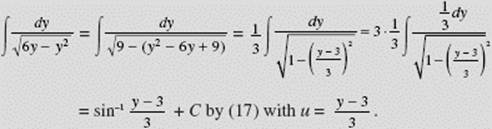
EXAMPLE 34
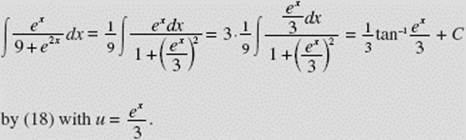
EXAMPLE 35
EXAMPLE 36
EXAMPLE 37
EXAMPLE 38
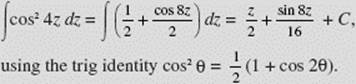
EXAMPLE 39
EXAMPLE 40
EXAMPLE 41
BC ONLY