Calculus AB and Calculus BC
CHAPTER 5 Antidifferentiation
C. INTEGRATION BY PARTIAL FRACTIONS
The method of partial fractions makes it possible to express a rational function ![]() as a sum of simpler fractions. Here f (x) and g(x) are real polynomials in x and it is assumed that
as a sum of simpler fractions. Here f (x) and g(x) are real polynomials in x and it is assumed that ![]() is a proper fraction; that is, that f (x) is of lower degree than g(x). If not, we divide f (x) by g(x) to express the given rational function as the sum of a polynomial and a proper rational function. Thus,
is a proper fraction; that is, that f (x) is of lower degree than g(x). If not, we divide f (x) by g(x) to express the given rational function as the sum of a polynomial and a proper rational function. Thus,
![]()
where the fraction on the right is proper.
Theoretically, every real polynomial can be expressed as a product of (powers of) real linear factors and (powers of) real quadratic factors. †
In the following, the capital letters denote constants to be determined. We consider only nonrepeating linear factors. For each distinct linear factor (x − a) of g(x) we set up one partial fraction of the type ![]() The techniques for determining the unknown constants are illustrated in the following examples.
The techniques for determining the unknown constants are illustrated in the following examples.
Examples 42–47 are BC ONLY.
EXAMPLE 42
Find ![]()
SOLUTION: We factor the denominator and then set
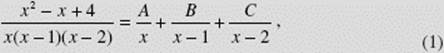
where the constants A, B, and C are to be determined. It follows that
![]()
Since the polynomial on the right in (2) is to be identical to the one on the left, we can find the constants by either of the following methods:
METHOD ONE. We expand and combine the terms on the right in (2), getting
x2 − x + 4 = (A + B + C)x2 − (3A + 2B + C)x + 2A.
We then equate coefficients of like powers in x and solve simultaneously. Thus
|
using the coefficients of x2, we get |
1 = A + B + C; |
|
using the coefficients of x, we get |
−1 = −(3A + 2B + C); |
|
using the constant coefficient, |
4 = 2A |
These equations yield A = 2, B = −4, C = 3.
METHOD TWO. Although equation (1) above is meaningless for x = 0, x = 1, or x = 2, it is still true that equation (2) must hold even for these special values. We see, in (2), that
|
if x = 0, |
then 4 = 2A and A = 2; |
|
if x = 1, |
then 4 = −B and B = −4; |
|
if x = 2, |
then 6 = 2C and C = 3. |
The second method is shorter than the first and more convenient when the denominator of the given fraction can be decomposed into nonrepeating linear factors.
Finally, then, the original integral equals
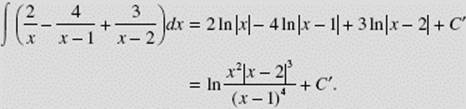
[The symbol “C′” appears here for the constant of integration because C was used in simplifying the original rational function.]
† In the Topical Outline for Calculus BC, integration by partial fractions is restricted to “simple partial fractions (nonrepeating linear factors only).”