Calculus AB and Calculus BC
CHAPTER 7 Applications of Integration to Geometry
B. VOLUME
B1. Solids with Known Cross Sections
If the area of a cross section of a solid is known and can be expressed in terms of x, then the volume of a typical slice, ΔV, can be determined. The volume of the solid is obtained, as usual, by letting the number of slices increase indefinitely. In Figure N7–9, the slices are taken perpendicular to the x-axis so that ΔV = A(x) Δx, where A(x) is the area of a cross section and Δx is the thickness of the slice.
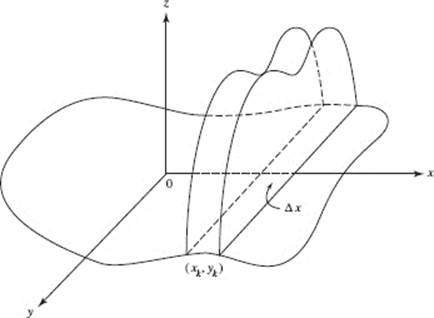
FIGURE N7–9
EXAMPLE 5
A solid has as its base the circle x2 + y2 = 9, and all cross sections parallel to the y-axis are squares. Find the volume of the solid.
SOLUTION:
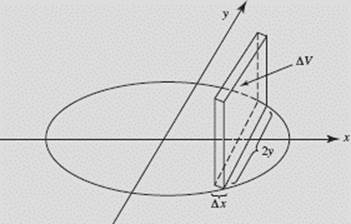
FIGURE N7–10
In Figure N7–10 the element of volume is a square prism with sides of length 2y and thickness Δx, so
ΔV = (2y)2 Δx = 4y2 Δx = 4(9 − x2) Δx.
Now, using symmetry across the y-axis, we find the volume of the solid:
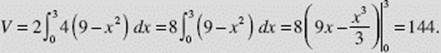
Questions 25, 26, and 27 in the Practice Exercises illustrate solids with known cross sections.
When the cross section of a solid is a circle, a typical slice is a disk. When the cross section is the region between two circles, a typical slice is a washer—a disk with a hole in it. Both of these solids, which are special cases of solids with known cross sections, can be generated by revolving a plane area about a fixed line.
B2. Solids of Revolution
A solid of revolution is obtained when a plane region is revolved about a fixed line, called the axis of revolution. There are two major methods of obtaining the volume of a solid of revolution “disks” and “washers.”
DISKS
The region bounded by a curve and the x-axis is revolved around the x-axis, forming the solid of revolution seen in Figure N7–11. We think of the “rectangular” strip” of the region at the left as generating the solid disk, ΔV (an element of the volume), shown at the right.
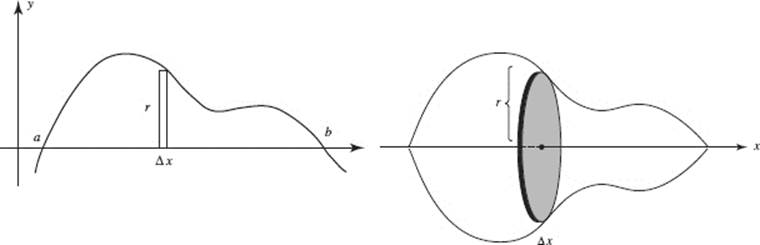
FIGURE N7–11
This disk is a cylinder whose radius, r, is the height of the rectangular strip, and whose height is the thickness of the strip, Δx. Thus
![]()
EXAMPLE 6
Find the volume of a sphere of radius r.
SOLUTION: If the region bounded by a semicircle (with center O and radius r) and its diameter is revolved about the x-axis, the solid of revolution obtained is a sphere of radius r, as seen in Figure N7–12.
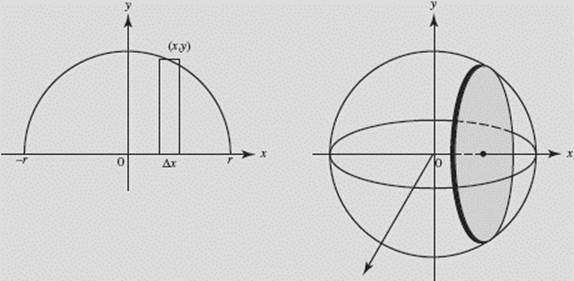
FIGURE N7–12
The volume ΔV of a typical disk is given by ΔV = π y2 Δx. The equation of the circle is x2 + y2 = r2. To find the volume of the sphere, we form a Riemann sum whose limit as n becomes infinite is a definite integral. Then,
![]()
EXAMPLE 7
Find the volume of the solid generated when the region bounded by y = x2, x = 2, and y = 0 is rotated about the line x = 2 as shown in Figure N7–13.
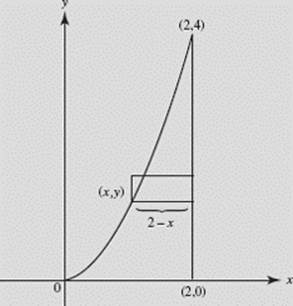
SOLUTION:
Disk.
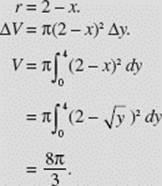
FIGURE N7–13
See Questions 18, 49, 51, 52, and 53 in the Practice Exercises for examples of finding volumes by disks.
WASHERS
A washer is a disk with a hole in it. The volume may be regarded as the difference in the volumes of two concentric disks. As an example, consider the volume of the solid of revolution formed when the region bounded by the two curves seen in Figure N7–14 is revolved around the x-axis. We think of the rectangular strip of the region at the left as generating the washer, ΔV (an element of the volume), shown at the right.
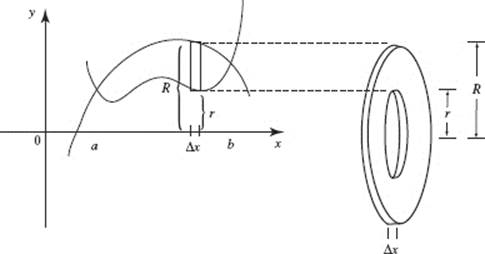
FIGURE N7–14
This washer’s height is the thickness of the rectangular strip, Δx. The washer is a disk whose outer radius, R, is the distance to the top of the rectangular strip, with the disk of inner radius r (the distance to the bottom of the strip) removed. Thus:
![]()
EXAMPLE 8
Find the volume obtained when the region bounded by y = x2 and y = 2x is revolved about the x-axis.
SOLUTION: The curves intersect at the origin and at (2, 4), as shown in Figure N7–15. Note that we distinguish between the two functions by letting (x, y1) be a point on the line and (x, y2) be a point on the parabola.
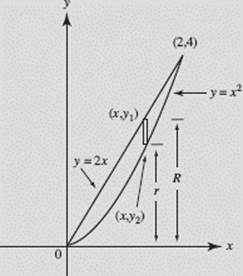
Washer.
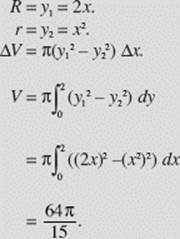
FIGURE N7–15
EXAMPLE 9
Find the volume of the solid generated when the region bounded by y = x2, x = 2, and y = 0 is rotated about the y-axis, as shown in Figure N7–16.
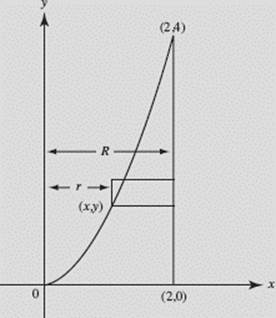
SOLUTION:
Washer.
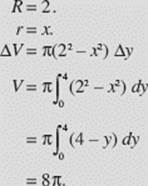
FIGURE N7–16
See Questions 19, 21, 48, 50, and 54 in the Practice Exercises for examples in which washers are regarded as the differences of two disks.
Occasionally when more than one method is satisfactory we try to use the most efficient. In the answers to each question in the Practice Exercises, a sketch is shown and the type and volume of a typical element are given. The required volume is then found by letting the number of elements become infinite and applying the Fundamental Theorem.
SHELLS‡
A cylindrical shell may be regarded as the outer skin of a cylinder. Its volume is the volume of the rectangular solid formed when this skin is peeled from the cylinder and flattened out. As an example, consider the volume of the solid of revolution formed when the region bounded by the two curves seen in Figure N7–17 is revolved around the y-axis. We think of the rectangular strip of the region at the left as generating the shell, ΔV (an element of the volume), shown at the right.
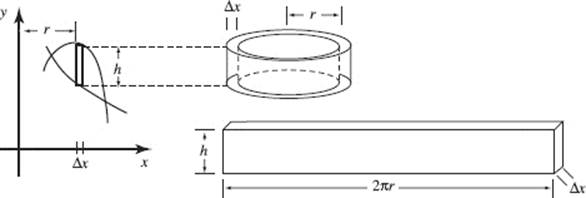
FIGURE N7–17
This shell’s radius, r, is the distance from the axis to the rectangular strip, and its height is the height of the rectangular strip, h. When the shell is unwound and flattened to form a rectangular solid, the length of the solid is the circumference of the cylinder, 2πr, its height is the height of the cylinder, h, and its thickness is the thickness of the rectangular strip, Δx. Thus:
![]()
‡Examples 10–12 involve finding volumes by the method of shells. Although shells are not included in the Topic Outline, we include this method here because it is often the most efficient (and elegant) way to find a volume. No question requiring shells will appear on the AP exam.
EXAMPLE 10
Find the volume of the solid generated when the region bounded by y = x2, x = 2, and y = 0 is rotated about the line x = 2. See Figure N7–18.
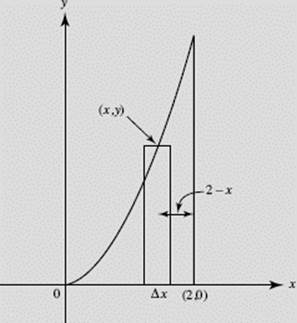
SOLUTION:
About x = 2.
Shell.
(Note that we obtained the same result using disks in Example 7.)
FIGURE N7–18
EXAMPLE 11
The region bounded by y = 3x − x2 and y = x is rotated about the y-axis. Find the volume of the solid obtained. See Figure N7–19.
SOLUTION:
About the y-axis.
Shell.
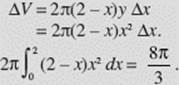
FIGURE N7–19
EXAMPLE 12
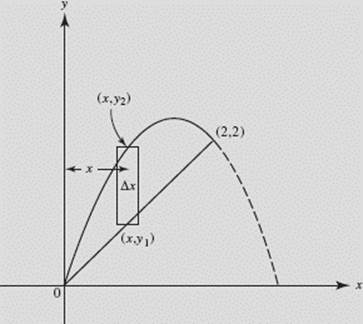
Find the volume obtained when the region bounded by y = x2 and y = 2x is revolved about the x-axis.
SOLUTION: The curves intersect at the origin and at (2,4), as shown in Figure N7–20. Note that we distinguish between the two functions by letting (x1, y) be a point on the line and (x2, y) be a point on the parabola.
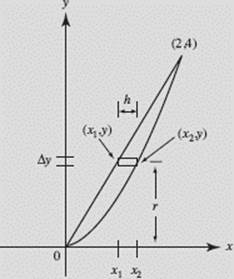
Shell.
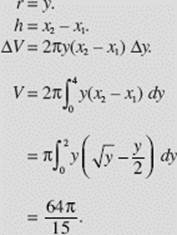
(Note that we obtained the same result using washers in Example 8.)
FIGURE N7–20
NOTE: In Examples 32 and 33 we consider finding the volumes of solids using shells that lead to improper integrals.
BC ONLY