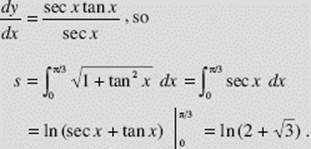Calculus AB and Calculus BC

CHAPTER 7 Applications of Integration to Geometry

C. ARC LENGTH

If the derivative of a function y = f (x) is continuous on the interval a x b, then the length s of the arc of the curve of y = f (x) from the point where x = a to the point where x = b is given by

Here a small piece of the curve is equal approximately to

As Δx → 0, the sum of these pieces approaches the definite integral above.

If the derivative of the function x = g(y) is continuous on the interval c ≤ y ≤ d, then the length s of the arc from y = c to y = d is given by

If a curve is defined parametrically by the equations x = x(t) and y = y(t), if the derivatives of the functions x(t) and y(t) are continuous on |t_a, t_b], (and if the curve does not intersect itself), then the length of the arc from t = t_a to t = t_b is given by

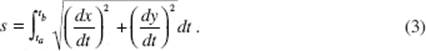
BC ONLY

The parenthetical clause above is equivalent to the requirement that the curve is traced out just once as t varies from t_a to t_b.

As indicated in Equation (4), formulas (1), (2), and (3) can all be derived easily from the very simple relation

and can be remembered by visualizing Figure N7–21.

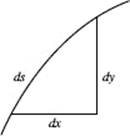
FIGURE N7–21

EXAMPLE 13

Find the length, to three decimal places, of the arc of y = x^3/2 from x = 1 to x = 8.

SOLUTION: Here

EXAMPLE 14

Find the length, to three decimal places, of the curve (x − 2)² = 4y³ from y = 0 to y = 1.

SOLUTION: Since x − 2 = 2y^3/2 and Equation (2) above yields

EXAMPLE 15

The position (x, y) of a particle at time t is given parametrically by x = t² and Find the distance the particle travels between t = 1 and t = 2.

SOLUTION: We can use (4): ds² = dx² + dy², where dx = 2 t dt and dy = (t² − 1) dt. Thus,

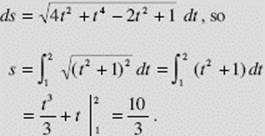
BC ONLY

EXAMPLE 16

Find the length of the arc of y = ln sec x from x = 0 to

SOLUTION: