The Calculus Primer (2011)
Part X. Partial Differentiation
Chapter 38. SINGULAR POINTS OF A CURVE
10—8.Basic Ideas. In the light of what has been said thus far about the meaning of a continuous curve, we may say, without proof, that if a curve is continuous throughout an interval, then, in general, there will exist a tangent to the curve at every point of the curve in that interval. This is true for nearly all curves. There are continuous curves, however, for which no tangent exists, but such curves are beyond the scope of this book. Thus, if RS is an arc of a curve, and if at the point P on RS there exists one and only one tangent, AB, to the curve, then point P is known as an ordinary point of the curve.
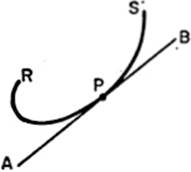
10—9.Singular Points of a Curve. If at a point P on a curve there exist two and only two distinct tangents, then that point is called a node. If the two tangents at a given point are not distinct, but coincide, we have what is called a cusp. There are several kinds of cusps: (1) if the curve in the neighborhood of a cusp lies partly on one side of the tangent and partly on the other side, the point is known as a cusp of the first kind; (2) if the curve lies entirely on one side of the common tangent (in the region of tangency), the point is known as a cusp of the second kind; (3) if there are two distinct cusps at the same point, it is known as a point of osculation.
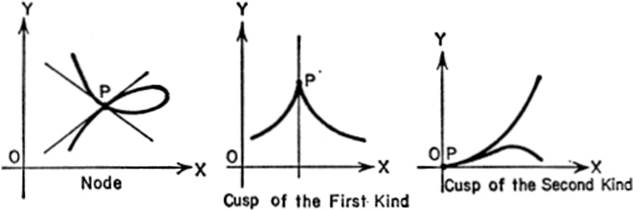
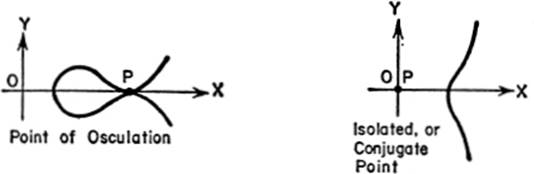
All points having two and only two tangents, whether real or imaginary, distinct or coincident, are called double points of the curve. Thus nodes and cusps of all kinds are double points. Triple points are such points on a curve for which there are three tangents; similarly for quadruple points, etc. An isolated point on a curve is also called a conjugate point. All points that are not ordinary points are known as singular points.
The conditions necessary for the existence of a singular point (x1,y1) on a curve f(x,y) = 0 are that
The reason for this will become clear when considering equation [1], §10—5, when applied to the point (x1,y1):
whenever 
and 
are both equal to zero, the value of 
becomes – 
, which is indeterminate; hence nothing can be said about the tangent at such a point.
It should be noted, in passing, that if 
≠ 0, but = 0, then the value of 
= 
= ± ∞ ; this means that the tangent to the curve at (x1,y1) is perpendicular to the X-axis, having the equation x = x1.
10—10.Conditions for Singular Points. Without giving the proofs, we may state the conditions to be satisfied at singular points:
and, in addition,
(I) for a node:
(II) for a cusp:
(III) for isolated points:
EXAMPLE. Prove that the curve y2 = x5 + z4 has a singular point at the origin.
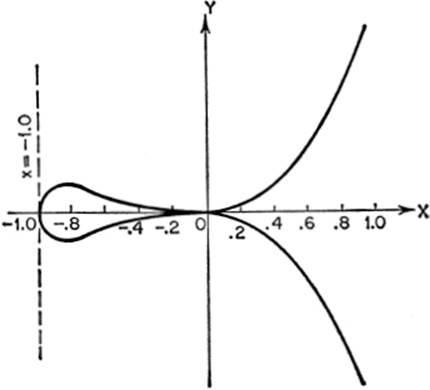
Solution.
f(x,y) = y2 − x5 − x4 = 0.
At (0,0), 
= −5x4 − 4x3 = 0; = 2y = 0;
therefore the fundamental conditions for a singular point are satisfied.
Furthermore, at the point (0,0), we have:
therefore
showing that the point (0,0) is either a cusp or a point of osculation. The curve is symmetrical with respect to the X-axis; moreover, it extends to the left of the Y-axis as far as x = − 1, as may be seen from the equation by solving for 
Hence the origin is a point of osculation, since there is a distinct cusp on either side of the Y-axis.
EXERCISE 10—3
1. Prove that the curve x3 − y2 = 0 has a cusp of the first kind at the point (0,0).
2. Prove that the curve y3 = 3x2 + 4x3 has a cusp of the first kind at the origin.
3. Prove that the origin is an ordinary point of the curve x = x3 + y3 + y.
4. Prove that the point (1, −1) is a node of the curve
(x − l)2 + y(y + l)2 = 0.
5. Prove that the curve x3 + y3 = 3xy has a node at the origin.
6. Prove that none of the following curves can have singular points of the kind discussed above:
(a) y = cos x
(b) y = aex
(c) x2 + y2 = k2
(d) xy = k
EXERCISE 10—4
Review
1. Find the value of each of the following:
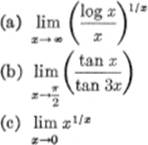
2. Find the total differential:
(a) Z = ax2 + by3
(b) Z = ax2y3
(c) Z = xy
3. Find the rectangle of maximum area inscribed in a semicircle of radius r.
4. If the function x·f(x) is continuous, find the equation whose solution gives values of x which make this function a maximum or a minimum.
5. Examine the following for points of inflection:
(a) x3 + y = ax2
(b) xy = x3 + 1
(c) y = ( x − a)3 − b
6. Find the radius of curvature at any point on the curve:
(a) y2 = 4px
(b) ex = sin y
7. What value of x will make the expression 
a maximum?