The Calculus Primer (2011)
Part XIV. The Definite Integral
Chapter 53. AREA UNDER A CURVE
14—5. Calculation of Areas. The discussion in §14—1 and §14—2 suggests a convenient method for calculating the area under a specific portion of a curve whose equation is known.
EXAMPLE 1. Find the area bounded by the parabola y = x2, the X-axis, and the ordinates x = 1 and x = 3.
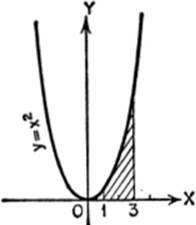
Solution.
EXAMPLE 2. Determine the area under the curve y2 = x and the line x = 9.
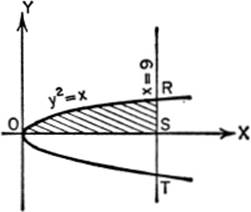
Solution. y2 = x, or y = x½.
Area ORS ![]()
![]()
Hence
area ORT = (2) (18) = 36.
EXAMPLE 3. Find the area under the curve y = cos x from x = – π/2 to x = π/2.
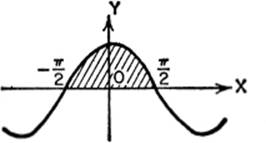
Solution.
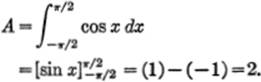
EXAMPLE 4. Find the area of the ellipse
![]()
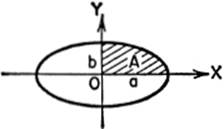
Solution. We first find the area under this curve lying in the first quadrant.
![]()
From the given equation,
![]()
Since the shaded area lies entirely in the first quadrant, both a and b are positive. We may therefore disregard the ± sign. Hence
![]()
By formula [68], page 376:
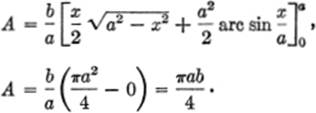
Hence, area of entire ellipse equals 4A, or πab,
The reader should note carefully that this method of determining areas is a perfectly general method only if y = f(x) is a continuous, single-valued function for values of x between x = a and x = 6, and if the limits a and b are finite. If either of these conditions does not hold, the method may or may not yield correct results, and special methods must be used.
EXERCISE 14—2
1. Find the area bounded by the parabola y = 6x2, the X-axis, and the ordinates at x = 2 and x = 4.
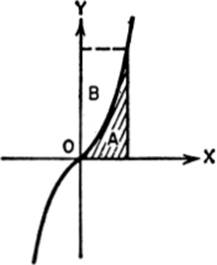
2. Find the area bounded by the parabola y2 = 4x, the Y-axis, and the line y = 4. Hint; First find the area A (the whole square); then find area B by difference.
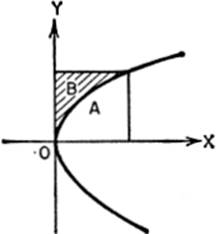
3. Find the shaded area, given that the equation of the curve is y = x2 — 4.
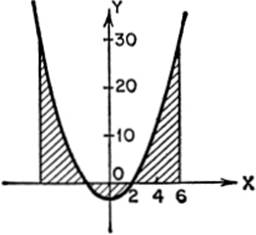
4. Find the area under one arch of the curve y = sin x, from x = 0 to x = π.
5. Find by integration the area included by the X-axis and the lines y = x + 4 and 2x + y = 10; verify the result by elementary geometry.
6. Find the area A bounded by the curve y = x3, the X-axis, and the line x = 2. Find also the unshaded area B.
7. Find the area of the figure bounded by the curve y = x2 + 2x – 6, the X-axis, and the ordinates at x = 2 and x = 6.
8. Find the area included between the hyperbola xy = a2, the X-axis, and the ordinates at x = a and x = b.
9. Find the area bounded by the parabola x½ + y½ = a½ and the coordinate axes.
10. Determine the area lying between the two parabolas y2 = 8x and x2 = 8y.
11. Prove that the area bounded by a parabola and any chord drawn perpendicular to its axis is equal to two-thirds of the rectangle in which this area is inscribed.
12. Show by integration that the area of the circle x2 + y2 = a2 equals πa2; first find the area in the first quadrant, using the integration formula ![]()
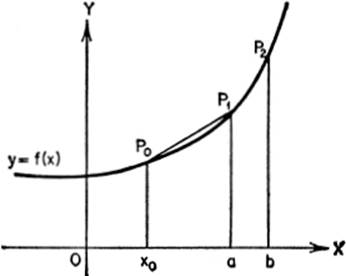
14—6. Length of Arc. The evaluation of a definite integral can also be used to determine the length of a particular arc of a curve whose equation is known. It will be recalled that
![]()
Now, consider the point P0 as a fixed point on the curve y = f(x), and regard the length along the curve of an arc to be generated by a moving, variable point (x,y). Reasoning as in §14—2, and integrating equation (1) above, we have:
![]()
remembering that the constant of integration is to be chosen so that s = 0 when x = x0.
Thus,
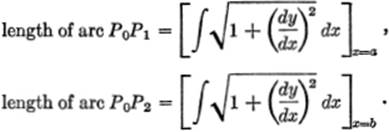
Hence, by difference,
![]()
We shall discuss the length of arc further in Chapter Fifteen.