The Calculus Primer (2011)

Reference Material from Other Branches of Mathematics

ALGEBRA

FACTORS:

a² ± 2ab + b² = (a ± 6)²

a² − b² = (a + b)(a − b)

a³ ± b³ = (a ± b)(a² / ab + b²)

a⁴ − b⁴ = (a² + b²) (a + b) (a − b)

a⁴ + b⁴ = (a² + b² + ab)(a² + b² − ab)

a²ⁿ − b²ⁿ = (aⁿ + bⁿ)(aⁿ − bⁿ)

EXPONENTS:

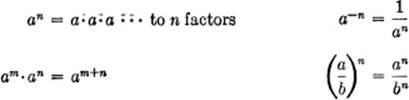
ROOTS:

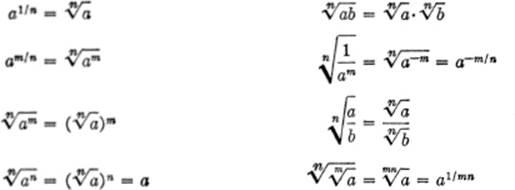
LOGARITHMS:

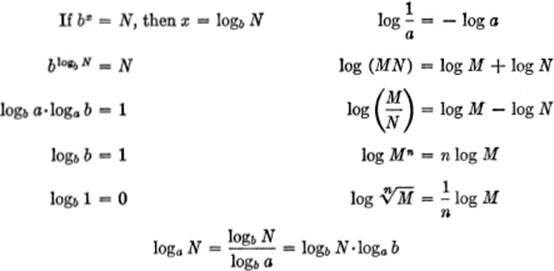
QUADRATIC EQUATIONS:

If r₁ and r₂ are the roots of the equation

ax² + bx + c = 0,

The discriminant Δ = b² − 4ac;

if Δ > 0, the roots are real and distinct;

if Δ = 0, the roots are real and equal;

if Δ < 0, the roots are complex.

(x − r₁) (x − r₂) = ax² + bx + c = 0;

PROGRESSIONS:

Arithmetic.l = a + (n − 1) d;

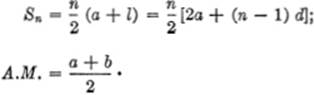
Geometric.l = arⁿ⁻¹;

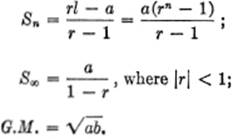
COMPLEX NUMBERS:

Ifa + bi = x + yi,then a = x and b = y.

Ifa + bi = r(cos θ + i sin θ),

thena = r cos θ,b = r sin θ,

[r(cos θ + i sin θ)]ⁿ = rⁿ(cos nθ + i sin nθ).

FACTORIALS:

n! = 1·2·3·4 ··· to n factors.

_nP_n = n!0! = 1

_nC_r = _nC_n−r

_nC_n = _nC₀ = 1

_nC₁ + _nC₂ + _nC₃ + ··· + _nC_n = 2ⁿ − 1;

_nC₀ + _nC₁ + _nC₂ + ··· + _nC_n = 2ⁿ.

BINOMIAL EXPANSION:

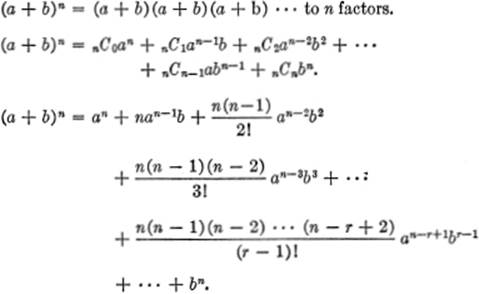
The rth term of (a + b)ⁿ is:

DETERMINANTS:

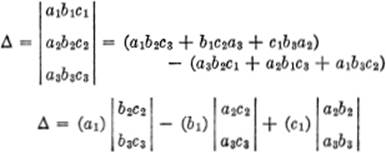
ZERO AND INFINITY:

The symbols 0 and ∞ are not to be regarded as “numbers” in these formulas:

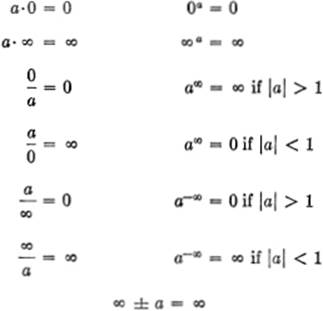
GEOMETRY

In the following formulas,

b = length of base

h = altitude

l = slant height

r = radius

m = median

d = diameter

θ = angle (in radians)

P = perimeter

C = circumference

S = arc length

s = semiperimeter

K = area

B = area of base

V = volume

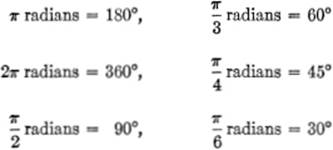
Triangle: P = a + b + c

K = bh =

Trapezoid: m = (b₁ + b₂)

K = h(b₁ + b₂) = mh

Circle: C = πd = 2πr

Sector: S = rθ

K = r²θ

Prism: V = Bh

Cylinder: (right circular) K = 2πrh + 2πr²

V = Bh = πr²h

Pyramid: V = Bh

Cone: (right circular) K = πrl + πr²; l =

V = Bh = πr²h

Sphere: K = 4πr²

V = πr³

Spherical triangle: K = , where E = (a° + b° + c°) − 180°.

TRIGONOMETRY

FUNDAMENTAL IDENTITIES:

sin²x + cos² x = 1;sec² x = 1 + tan² x;csc² x = 1 + cot² x.

TRANSFORMATIONS:

Functions of the Sum and Difference of Two Angles:

sin (x ± y) = sin x cos y ± cos x sin y,

cos (x ± y) = cos x cos y / sin x sin y,

Multiple Angle Formulas:

sin 2x = 2 sin x cos x,

cos 2x = cos² x − sin² x = 2 cos² x − 1 = 1 − 2 sin² x,

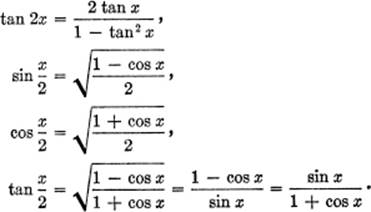
Sum and Product Formulas:

sin x + sin y = 2 sin (x + y) cos (x − y),
sin x − sin y = 2 cos (x + y) sin (x − y),
cos x + cos y = 2 cos (x + y) cos (x − y),
cos x − cos y = −2 sin (x + y) sin (x − y),
sin x sin y = cos (x − y) − cos (x + y),
sin x cos y = sin (x − y) + sin (x + y),
cos x cos y = cos (x − y) + cos (x + y). 

sin² x − sin² y = sin (x + y) sin (x − y), 
cos² x − cos² y = − sin (x + y) sin (x − y), 
cos² x − sin² y = cos (x + y) cos (x − y), 

sin² x = − cos 2x,
cos² x = + cos 2x.

PLANE TRIANGLES:

a, b, c = sides of the triangle

A, B, C = opposite angles of the triangle

R = radius of the circumscribed circle

K = area of the triangle

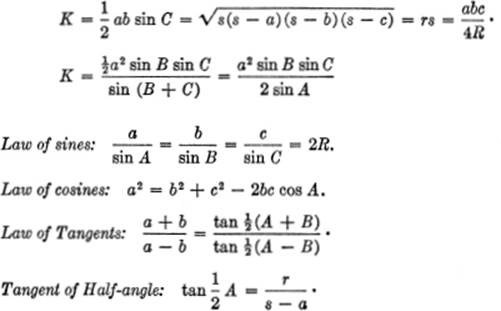
FUNCTIONS OF SPECIAL ANGLES:

PLANE ANALYTIC GEOMETRY

FUNDAMENTAL RELATIONS:

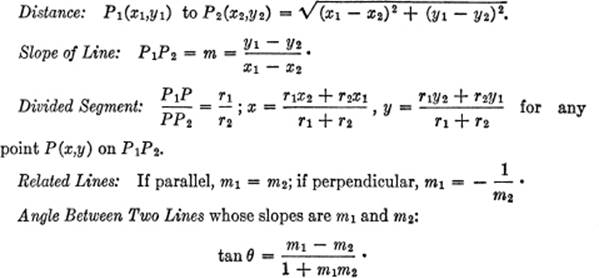
EQUATIONS OF A STRAIGHT LINE:

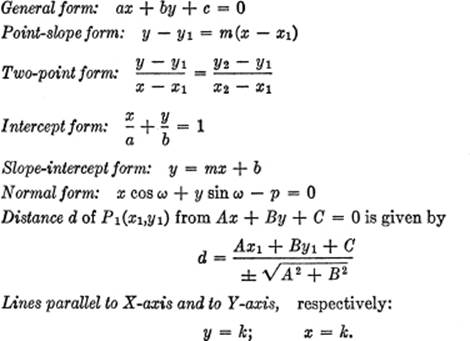
POLAR COORDINATES:

If P(x,y) ≡ P(r,θ), then

CONIC SECTIONS:

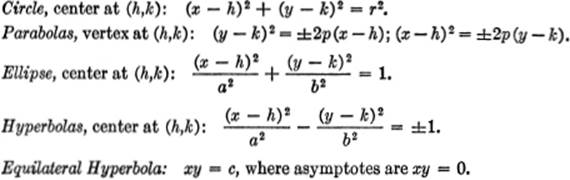
CURVES FOR REFERENCE

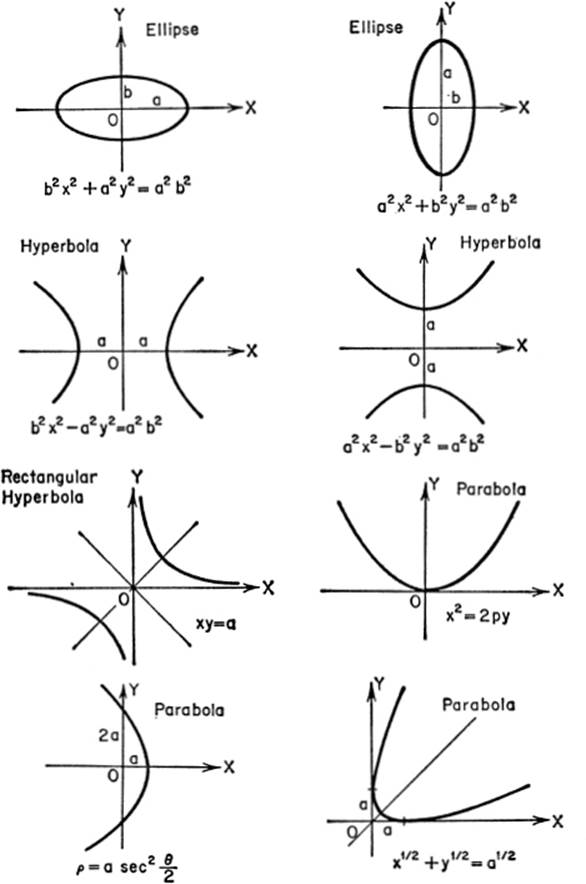
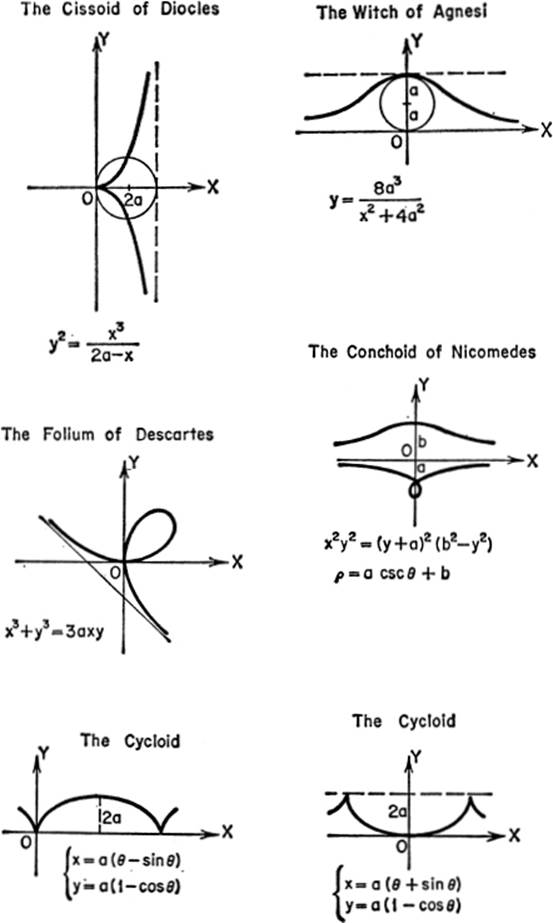
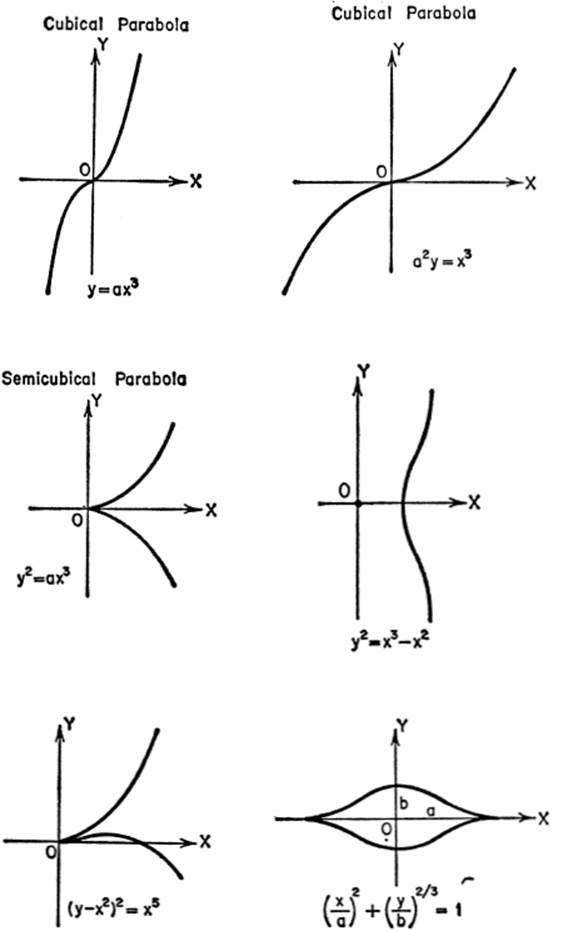
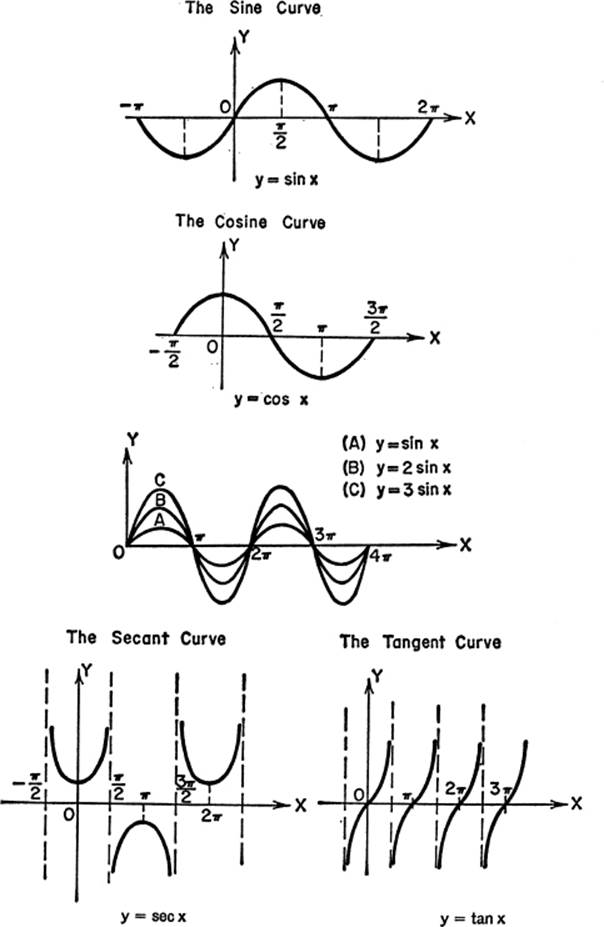
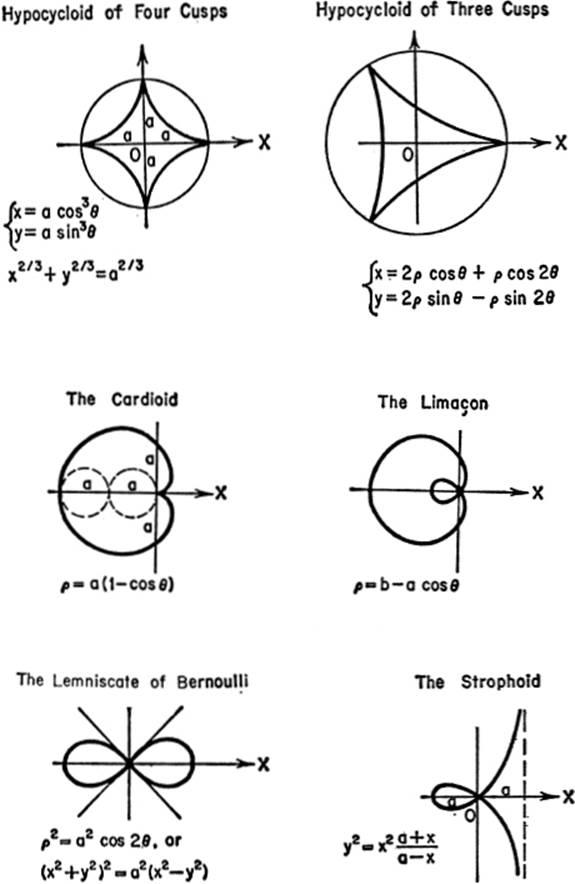
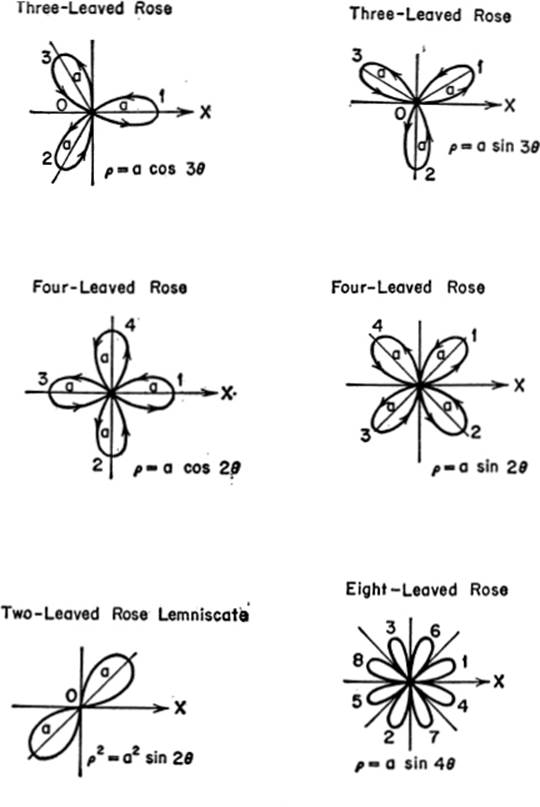
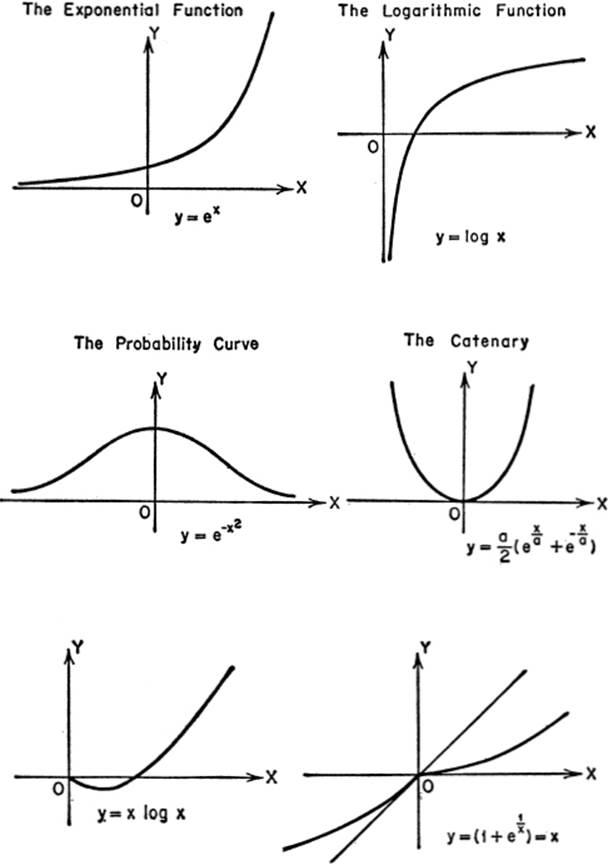
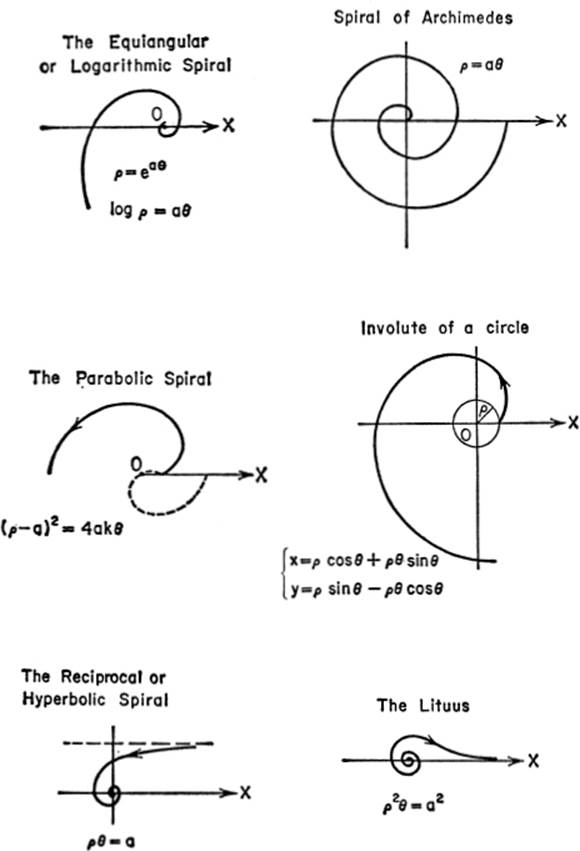
SOLID ANALYTIC GEOMETRY

FUNDAMENTAL RELATIONS

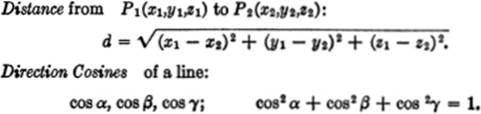
EQUATIONS OF A PLANE:

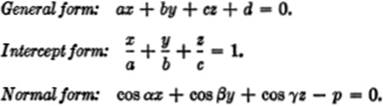
EQUATIONS OF A LINE:

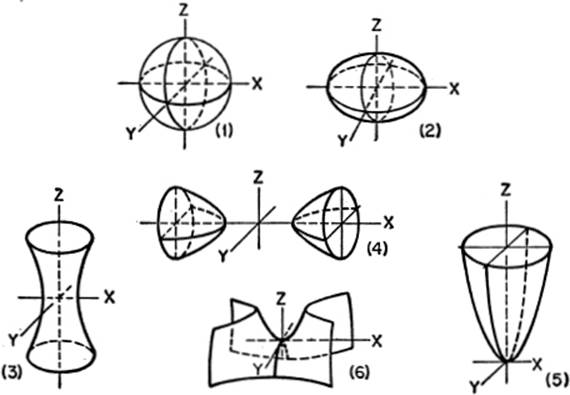
QUADRIC SURFACES

(1)Sphere with center at (0,0,0):

x² + y² + z² = r².

(2)Ellipsoid with center at (0,0,0):

(3)Hyperboloid of one sheet:

(4)Hyperboloid of two sheets:

(5)Elliptic Paraboloid:

(6)Hyperbolic Paraboloid (saddle surface) :

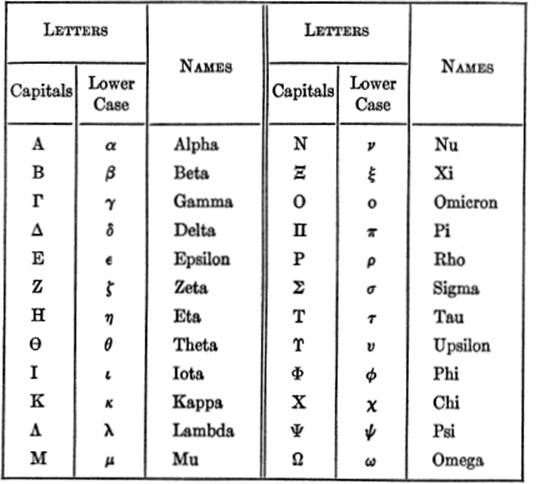
GREEK ALPHABET