Discrete Nabla Integral - Nabla Fractional Calculus - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

3. Nabla Fractional Calculus

3.6. Discrete Nabla Integral

In this section we define the nabla definite and indefinite integral, give several of their properties, and present a nabla fundamental theorem of calculus.

Definition 3.31.

Assume $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ and $$b \in \mathbb{N}_{a}$$ . Then the nabla integral of f from a to b is defined by

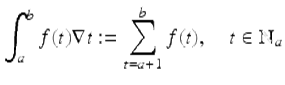
$$\displaystyle{\int _{a}^{b}f(t)\nabla t:=\sum _{ t=a+1}^{b}f(t),\quad t \in \mathbb{N}_{ a}}$$

with the convention that

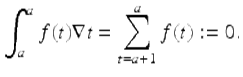
$$\displaystyle{\int _{a}^{a}f(t)\nabla t =\sum _{ t=a+1}^{a}f(t):= 0.}$$

Note that even if f had the domain $$\mathbb{N}_{a}$$ instead of $$\mathbb{N}_{a+1}$$ the value of the integral $$\int _{a}^{b}f(t)\nabla t$$ does not depend on the value of f at a. Also note if $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ , then $$F(t):=\int _{ a}^{t}f(\tau )\nabla \tau$$ is defined on $$\mathbb{N}_{a}$$ with F(a) = 0.

The following theorem gives some important properties of this nabla integral.

Theorem 3.32.

Assume $$f,g: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ , $$b,c,d \in \mathbb{N}_{a}$$ , b ≤ c ≤ d, and $$\alpha \in \mathbb{R}$$ . Then

(i)

$$\int _{b}^{c}\alpha f(t)\nabla t =\alpha \int _{ b}^{c}f(t)\nabla t;$$

(ii)

$$\int _{b}^{c}(f(t) + g(t))\nabla t =\int _{ b}^{c}f(t)\nabla t +\int _{ b}^{c}g(t)\nabla t;$$

(iii)

$$\int _{b}^{b}f(t)\nabla t = 0;$$

(iv)

$$\int _{b}^{d}f(t)\nabla t =\int _{ b}^{c}f(t)\nabla t +\int _{ c}^{d}f(t)\nabla t;$$

(v)

$$\vert \int _{b}^{c}f(t)\nabla t\vert \leq \int _{b}^{c}\vert f(t)\vert \nabla t;$$

(vi)

if $$F(t):=\int _{ b}^{t}f(s)\nabla s$$ , for $$t \in \mathbb{N}_{b}^{c},$$ then ∇F(t) = f(t), $$t \in \mathbb{N}_{b+1}^{c}$$ ;

(vii)

if f(t) ≥ g(t) for $$t \in \mathbb{N}_{b+1}^{c},$$ then $$\int _{b}^{c}f(t)\nabla t \geq \int _{b}^{c}g(t)\nabla t$$ .

Proof.

To see that (vi) holds, assume

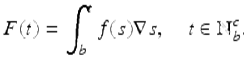
$$\displaystyle{F(t) =\int _{ b}^{t}f(s)\nabla s,\quad t \in \mathbb{N}_{ b}^{c}.}$$

Then, for $$t \in \mathbb{N}_{b+1}^{c}$$ , we have that

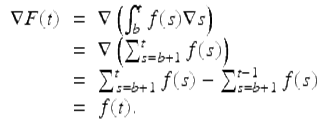
$$\displaystyle\begin{array}{rcl} \nabla F(t)& =& \nabla \left (\int _{b}^{t}f(s)\nabla s\right ) {}\\ & =& \nabla \left (\sum _{s=b+1}^{t}f(s)\right ) {}\\ & =& \sum _{s=b+1}^{t}f(s) -\sum _{ s=b+1}^{t-1}f(s) {}\\ & =& f(t). {}\\ \end{array}$$

Hence property (vi) holds. All the other properties of the nabla integral in this theorem hold since the corresponding properties for the summations hold. □ 

Definition 3.33.

Assume $$f: \mathbb{N}_{a+1}^{b} \rightarrow \mathbb{R}$$ . We say $$F: \mathbb{N}_{a}^{b} \rightarrow \mathbb{R}$$ is a nabla antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ provided

$$\displaystyle{\nabla F(t) = f(t),\quad t \in \mathbb{N}_{a+1}^{b}.}$$

If $$f: \mathbb{N}_{a+1}^{b} \rightarrow \mathbb{R}$$ , then if we define F by

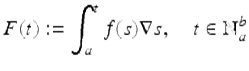
$$\displaystyle{F(t):=\int _{ a}^{t}f(s)\nabla s,\quad t \in \mathbb{N}_{ a}^{b}}$$

we have from part (vi) of Theorem 3.32 that ∇F(t) = f(t), for $$t \in \mathbb{N}_{a+1}^{b}$$ , that is, F(t) is a nabla antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Next we show that if $$f: \mathbb{N}_{a+1}^{b} \rightarrow \mathbb{R}$$ , then f(t) has infinitely many antidifferences on $$\mathbb{N}_{a}^{b}$$ .

Theorem 3.34.

If $$f: \mathbb{N}_{a+1}^{b} \rightarrow \mathbb{R}$$ and G(t) is a nabla antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ , then $$F(t) = G(t) + C$$ , where C is a constant, is a general nabla antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ .

Proof.

Assume G(t) is a nabla antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Let $$F(t):= G(t) + C$$ , $$t \in \mathbb{N}_{a}^{b}$$ , where C is a constant. Then

$$\displaystyle{\nabla F(t) = \nabla G(t) = f(t),\quad t \in \mathbb{N}_{a+1}^{b},}$$

and so, F(t) is a antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ .

Conversely, assume F(t) is a nabla antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Then

$$\displaystyle{\nabla (F(t) - G(t)) = \nabla F(t) -\nabla G(t) = f(t) - f(t) = 0}$$

for $$t \in \mathbb{N}_{a+1}^{b}$$ . This implies $$F(t) - G(t) = C$$ , for $$t \in \mathbb{N}_{a}^{b}$$ , where C is a constant. Hence

$$\displaystyle{F(t):= G(t) + C,\quad t \in \mathbb{N}_{a}^{b}.}$$

This completes the proof. □ 

Definition 3.35.

If $$f: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ , then the nabla indefinite integral of f is defined by

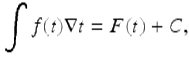
$$\displaystyle{\int f(t)\nabla t = F(t) + C,}$$

where F(t) is a nabla antidifference of f(t) and C is an arbitrary constant.

Since any formula for a nabla derivative gives us a formula for an indefinite integral, we have the following theorem.

Theorem 3.36.

The following hold:

(i)

$$\int \alpha ^{t+\beta }\nabla t = \frac{\alpha } {\alpha -1}\alpha ^{t+\beta } + C,\quad \alpha \neq 1;$$

(ii)

$$\int (t-\alpha )^{\overline{r}}\nabla t = \frac{1} {r+1}(t-\alpha )^{\overline{r + 1}} + C,\quad r\neq - 1;$$

(iii)

$$\int (\alpha -\rho (t))^{\overline{r}}\nabla t = - \frac{1} {r+1}(\alpha -t)^{\overline{r + 1}} + C,\quad r\neq - 1;$$

(iv)

$$\int p(t)\;E_{p}(t,a)\nabla t = E_{p}(t,a) + C,\quad \mbox{ if}\quad p \in \mathcal{R};$$

(v)

$$\int p(t)\mbox{ Cosh}_{p}(t,a)\nabla t = \mbox{ Sinh}_{p}(t,a) + C,\quad \mbox{ if}\quad \pm p \in \mathcal{R};$$

(vi)

$$\int p(t)\mbox{ Sinh}_{p}(t,a)\nabla t = \mbox{ Cosh}_{p}(t,a) + C,\quad \mbox{ if}\quad \pm p \in \mathcal{R};$$

(vii)

$$\int p(t)\mbox{ Cos}_{p}(t,a)\nabla t = \mbox{ Sin}_{p}(t,a) + C,\quad \mbox{ if}\quad \pm ip \in \mathcal{R};$$

(viii)

$$\int p(t)\mbox{ Sin}_{p}(t,a)\nabla t = -\mbox{ Cos}_{p}(t,a) + C,\quad \mbox{ if}\quad \pm ip \in \mathcal{R},$$

where C is an arbitrary constant.

Proof.

The formula

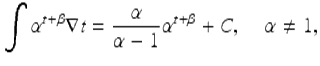
$$\displaystyle{\int \alpha ^{t+\beta }\nabla t = \frac{\alpha } {\alpha -1}\alpha ^{t+\beta } + C,\quad \alpha \neq 1,}$$

is clear when α = 0, and for α ≠ 0 it follows from part (iv) of Theorem 3.1. Parts (ii) and (iii) of this theorem follow from the power rules (3.3) and (3.4), respectively. Part (iv) of this theorem follows from part (iv) of Theorem 3.11. Parts (v) and (vi) of this theorem follow from parts (iv) and (iii) of Theorem 3.16, respectively. Finally, parts (vii) and (viii) of this theorem follow from parts (iv) and (iii) of Theorem 3.19, respectively. □ 

We now state and prove the fundamental theorem for the nabla calculus.

Theorem 3.37 (Fundamental Theorem of Nabla Calculus).

We assume $$f: \mathbb{N}_{a+1}^{b} \rightarrow \mathbb{R}$$ and F is any nabla antidifference of f on $$\mathbb{N}_{a}^{b}$$ . Then

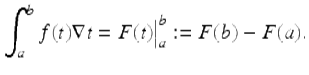
$$\displaystyle{\int _{a}^{b}f(t)\nabla t = F(t)\big\vert _{ a}^{b}:= F(b) - F(a).}$$

Proof.

By Theorem 3.32, (vi), we have that G defined by $$G(t):=\int _{ a}^{t}f(s)\nabla s$$ , for $$t \in \mathbb{N}_{a}^{b},$$ is a nabla antidifference of f on $$\mathbb{N}_{a}^{b}$$ . Since F is a nabla antidifference of f on $$\mathbb{N}_{a}^{b}$$ , it follows from Theorem 3.34 that $$F(t) = G(t) + C$$ , $$t \in \mathbb{N}_{a}^{b},$$ for some constant C. Hence,

$$\displaystyle\begin{array}{rcl} F(t)\big\vert _{a}^{b}& =& F(b) - F(a) {}\\ & =& [G(b) + C] - [G(a) + C] {}\\ & =& G(b) - G(a) {}\\ & =& \int _{a}^{b}f(s)\nabla s -\int _{ a}^{a}f(s)\nabla s {}\\ & =& \int _{a}^{b}f(s)\nabla s. {}\\ \end{array}$$

This completes the proof. □ 

Example 3.38.

Assume p ≠ 0, 1 is a constant. Use the integration formula

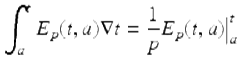
$$\displaystyle{\int _{a}^{t}E_{ p}(t,a)\nabla t = \frac{1} {p}E_{p}(t,a)\big\vert _{a}^{t}}$$

to evaluate the integral $$\int _{0}^{4}f(t)\nabla t,$$ where $$f(t):= (-3)^{-t},$$ $$t \in \mathbb{N}_{0}$$ . We calculate

$$\displaystyle\begin{array}{rcl} \int _{0}^{4}(-3)^{-t}\nabla t& =& \int _{ 0}^{4}(1 - 4)^{0-t}\nabla t {}\\ & =& \int _{0}^{4}E_{ 4}(t,0)\nabla t {}\\ & =& \frac{1} {4}E_{4}(t,0)\big\vert _{0}^{4} {}\\ & =& \frac{1} {4}[E_{4}(4,0) - E_{4}(0,0)] {}\\ & =& \frac{1} {4}[(-3)^{-4} - 1] {}\\ & =& -\frac{20} {81}. {}\\ \end{array}$$

Check this answer by using part (i) in Theorem 3.36.

Using the product rule (part (v) in Theorem 3.1) we can prove the following integration by parts formulas.

Theorem 3.39 (Integration by Parts).

Given two functions $$u,v: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ and $$b,c \in \mathbb{N}_{a}$$ , b < c, we have the integration by parts formulas:

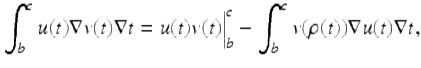
$$\displaystyle{ \int _{b}^{c}u(t)\nabla v(t)\nabla t = u(t)v(t)\Big\vert _{ b}^{c} -\int _{ b}^{c}v(\rho (t))\nabla u(t)\nabla t, }$$

(3.19)

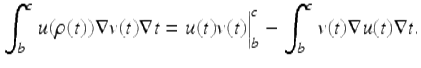
$$\displaystyle{ \int _{b}^{c}u(\rho (t))\nabla v(t)\nabla t = u(t)v(t)\Big\vert _{ b}^{c} -\int _{ b}^{c}v(t)\nabla u(t)\nabla t. }$$

(3.20)

Example 3.40.

Given $$f(t) = (t - 1)3^{1-t}$$ for $$t \in \mathbb{N}_{1}$$ , evaluate the integral $$\int _{1}^{t}f(\tau )\nabla \tau$$ . Note that

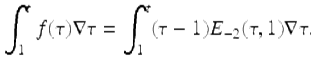
$$\displaystyle{\int _{1}^{t}f(\tau )\nabla \tau =\int _{ 1}^{t}(\tau -1)E_{ -2}(\tau,1)\nabla \tau.}$$

To set up to use the integration by parts formula (3.19), set

$$\displaystyle{u(\tau ) =\tau -1,\quad \nabla v(\tau ) = E_{-2}(\tau,1).}$$

It follows that

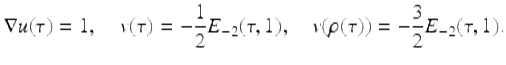
$$\displaystyle{\nabla u(\tau ) = 1,\quad v(\tau ) = -\frac{1} {2}E_{-2}(\tau,1),\quad v(\rho (\tau )) = -\frac{3} {2}E_{-2}(\tau,1).}$$

Hence, using the integration by parts formula (3.19), we get

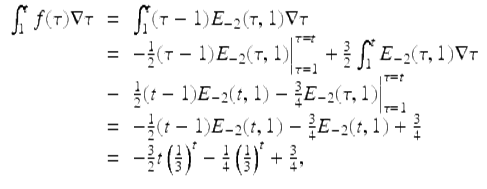
$$\displaystyle\begin{array}{rcl} \int _{1}^{t}f(\tau )\nabla \tau & =& \int _{ 1}^{t}(\tau -1)E_{ -2}(\tau,1)\nabla \tau {}\\ & =& -\frac{1} {2}(\tau -1)E_{-2}(\tau,1)\Big\vert _{\tau =1}^{\tau =t} + \frac{3} {2}\int _{1}^{t}E_{ -2}(\tau,1)\nabla \tau {}\\ &-& \frac{1} {2}(t - 1)E_{-2}(t,1) -\frac{3} {4}E_{-2}(\tau,1)\Big\vert _{\tau =1}^{\tau =t} {}\\ & =& -\frac{1} {2}(t - 1)E_{-2}(t,1) -\frac{3} {4}E_{-2}(t,1) + \frac{3} {4} {}\\ & =& -\frac{3} {2}t\left (\frac{1} {3}\right )^{t} -\frac{1} {4}\left (\frac{1} {3}\right )^{t} + \frac{3} {4}, {}\\ \end{array}$$

for $$t \in \mathbb{N}_{1}$$ .