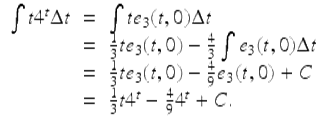The Delta Integral - Basic Difference Calculus - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

1. Basic Difference Calculus

1.5. The Delta Integral

First we define the delta definite integral.

Definition 1.49.

Assume $$f: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ and c ≤ d are in $$\mathbb{N}_{a}$$ , then

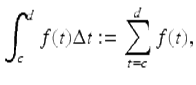
$$\displaystyle{ \int _{c}^{d}f(t)\Delta t:=\sum _{ t=c}^{d}f(t), }$$

(1.25)

where by convention $$\sum _{t=c}^{c-k}f(t):= 0,$$ whenever $$k \in \mathbb{N}_{1}.$$ We will define this to be the case even when f(t) is not defined for some (or all) values $$t \in \mathbb{N}_{c-k}.$$ In the sum in (1.25) it is understood that the index t takes on the values $$c,c + 1,c + 2,\ldots,d - 1$$ when d > c.

Note that the value of the integral $$\int _{c}^{d}f(t)\Delta t$$ does not depend on the value f(d). The following theorem gives some properties of this delta integral.

Theorem 1.50.

Assume $$f,g: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ , $$b,c,d \in \mathbb{N}_{a}$$ , b ≤ c ≤ d, and $$\alpha \in \mathbb{R}$$ . Then

(i)

$$\int _{b}^{c}\alpha f(t)\Delta t =\alpha \int _{ b}^{c}f(t)\Delta t;$$

(ii)

$$\int _{b}^{c}(f(t) + g(t))\Delta t =\int _{ b}^{c}f(t)\Delta t +\int _{ b}^{c}g(t)\Delta t;$$

(iii)

$$\int _{b}^{b}f(t)\Delta t = 0;$$

(iv)

$$\int _{b}^{d}f(t)\Delta t =\int _{ b}^{c}f(t)\Delta t +\int _{ c}^{d}f(t)\Delta t;$$

(v)

$$\vert \int _{b}^{c}f(t)\Delta t\vert \leq \int _{b}^{c}\vert f(t)\vert \Delta t;$$

(vi)

if $$F(t):=\int _{ b}^{t}f(s)\Delta s$$ , for $$t \in \mathbb{N}_{b}^{c},$$ then $$\Delta F(t) = f(t),$$ $$t \in \mathbb{N}_{b}^{c-1};$$

(vii)

if f(t) ≥ g(t), for $$t \in \mathbb{N}_{b}^{c-1},$$ then $$\int _{b}^{c}f(t)\Delta t \geq \int _{b}^{c}g(t)\Delta t.$$

Proof.

Most of these properties of the integral hold since the corresponding properties for sums hold. We leave the proof of this theorem to the reader. □ 

Definition 1.51.

Assume $$f: \mathbb{N}_{a}^{b} \rightarrow \mathbb{R}$$ . We say F is an antidifference of f on $$\mathbb{N}_{a}^{b}$$ provided

$$\displaystyle{\Delta F(t) = f(t),\quad t \in \mathbb{N}_{a}^{b-1}.}$$

Since $$\Delta \left (\frac{1} {2}3^{t}\right ) = 3^{t}$$ , $$t \in \mathbb{N}_{a}$$ , we have that $$F(t) = \frac{1} {2}3^{t}$$ is an antidifference of f(t) = 3 t on $$\mathbb{N}_{a}.$$

Theorem 1.52.

If $$f: \mathbb{N}_{a}^{b} \rightarrow \mathbb{R}$$ and G(t) is an antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ , then F(t) = G(t) + C, where C is an arbitrary constant, is a general antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ .

Proof.

Assume G(t) is an antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Let F(t): = G(t) + C, $$t \in \mathbb{N}_{a}^{b}$$ , where C is a constant. Then

$$\displaystyle{\Delta F(t) = \Delta G(t) = f(t),\quad t \in \mathbb{N}_{a}^{b},}$$

and so F(t) is an antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Next assume F(t) is an antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Then

$$\displaystyle{\Delta [F(t) - G(t)] = \Delta F(t) - \Delta G(t) = f(t) - f(t) = 0}$$

for $$t \in \mathbb{N}_{a}^{b-1}.$$ This implies (Exercise 1.1) F(t) − G(t) = C, for $$t \in \mathbb{N}_{a}^{b}$$ , where C is a constant. Hence F(t): = G(t) + C, for $$t \in \mathbb{N}_{a}^{b}.$$  □ 

Example 1.53.

Find the number of regions, R(n), the plane is divided into by n lines, where no two lines are parallel and no three lines intersect at the same point. Note that

$$\displaystyle{R(1) = 2,\quad R(2) = 4,\quad R(3) = 7,\quad R(4) = 11.}$$

To find R(n) for all $$n \in \mathbb{N}_{1}$$ , first convince yourself that for any $$n \in \mathbb{N}_{1}$$ ,

$$\displaystyle{R(n + 1) = R(n) + n + 1.}$$

It follows that

$$\displaystyle{\Delta R(n) = n + 1 = (n + 1)^{\underline{1}}.}$$

Since $$\frac{1} {2}(n + 1)^{\underline{2}}$$ is an antidifference of (n + 1) 1 , we have by Theorem 1.52 that

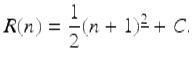
$$\displaystyle{R(n) = \frac{1} {2}(n + 1)^{\underline{2}} + C.}$$

Using R(1) = 2 we get that C = 1 and hence

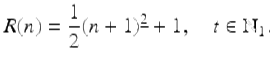
$$\displaystyle{R(n) = \frac{1} {2}(n + 1)^{\underline{2}} + 1,\quad t \in \mathbb{N}_{ 1}.}$$

Definition 1.54.

If $$f: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ , then the delta indefinite integral of f is defined by

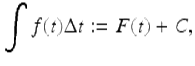
$$\displaystyle{\int f(t)\Delta t:= F(t) + C,}$$

where F is an antidifference of f and C is an arbitrary constant.

It is easy to verify that

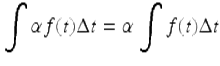
$$\displaystyle{\int \alpha f(t)\Delta t =\alpha \int f(t)\Delta t}$$

and

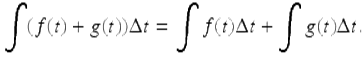
$$\displaystyle{\int (f(t) + g(t))\Delta t =\int f(t)\Delta t +\int g(t)\Delta t.}$$

Any formula for a delta derivative gives us a formula for an indefinite delta integral, so we have the following theorem.

Theorem 1.55.

Assume p, r, α are constants. Then the following hold:

(i)

$$\int (t-\alpha )^{\underline{r}}\Delta t = \frac{1} {r+1}(t-\alpha )^{\underline{r+1}} + C,\quad r\neq - 1;$$

(ii)

$$\int e_{p}(t,a)\Delta t = \frac{1} {p}e_{p}(t,a) + C,\quad p\neq 0,-1;$$

(iii)

$$\int \cosh _{p}(t,a)\Delta t = \frac{1} {p}\sinh _{p}(t,a) + C,\quad p\neq 0,\pm 1;$$

(iv)

$$\int \sinh _{p}(t,a)\Delta t = \frac{1} {p}\cosh _{p}(t,a) + C,\quad p\neq 0,\pm 1;$$

(v)

$$\int \cos _{p}(t,a)\Delta t = \frac{1} {p}\sin _{p}(t,a) + C,\quad p\neq 0,\pm i;$$

(vi)

$$\int \sin _{p}(t,a)\Delta t = -\frac{1} {p}\cos _{p}(t,a) + C,\quad p\neq 0,\pm i;$$

(vii)

$$\int (\alpha -\sigma (t))^{\underline{r}}\Delta t = \frac{-1} {r+1}(\alpha -t)^{\underline{r+1}} + C,\quad r\neq - 1;$$

(viii)

$$\int \binom{t}{r}\Delta t = \binom{t}{r + 1} + C;$$

(ix)

$$\int \binom{r + t}{t}\Delta t = \binom{r + t}{t - 1} + C;$$

(x)

$$\int (t - 1)\Gamma (t)\Delta t = \Gamma (t) + C;$$

(xi)

$$\int \alpha ^{t}\Delta t = \frac{1} {\alpha -1}\alpha ^{t} + C,\quad \alpha \neq 1,$$

where C is an arbitrary constant.

Theorem 1.56 (Fundamental Theorem for the Difference Calculus).

Assume $$f: \mathbb{N}_{a}^{b} \rightarrow \mathbb{R}$$ and F(t) is any antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Then

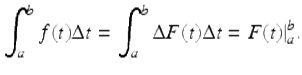
$$\displaystyle{\int _{a}^{b}f(t)\Delta t =\int _{ a}^{b}\Delta F(t)\Delta t = F(t)\vert _{ a}^{b}.}$$

(Here we use the common notation F(t)| a b := F(b) − F(a).)

Proof.

Assume F(t) is any antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Let

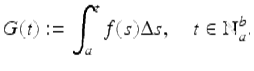
$$\displaystyle{G(t):=\int _{ a}^{t}f(s)\Delta s,\quad t \in \mathbb{N}_{ a}^{b}.}$$

Then by Theorem 1.50 (vi), G(t) is an antidifference of f(t) on $$\mathbb{N}_{a}^{b}$$ . Hence by Theorem 1.52, F(t) = G(t) + C, where C is a constant. Then

$$\displaystyle\begin{array}{rcl} F(t)\vert _{a}^{b}& =& F(b) - F(a) {}\\ & =& [(G(b) + C) - (G(a) + C)] {}\\ & =& G(b) - G(a) {}\\ & =& \int _{a}^{b}f(t)\Delta t. {}\\ \end{array}$$

This completes the proof. □ 

Example 1.57.

Use a delta integral to find the sum of the squares of the first n positive integers. Using k 2 = k 2 + k 1 we get

$$\displaystyle\begin{array}{rcl} \sum _{k=1}^{n}k^{2}& =& \int _{ 1}^{n+1}k^{2}\Delta k {}\\ & =& \int _{1}^{n+1}(k^{\underline{2}} + k^{\underline{1}})\Delta k {}\\ & =& \left [\frac{1} {3}k^{\underline{3}} + \frac{1} {2}k^{\underline{2}}\right ]_{ 1}^{n+1} {}\\ & =& \frac{1} {3}(n + 1)^{\underline{3}} + \frac{1} {2}(n + 1)^{\underline{2}} {}\\ & =& \frac{(n + 1)n(n - 1)} {3} + \frac{(n + 1)n} {2} {}\\ & =& \frac{n(n + 1)(2n + 1)} {6}. {}\\ \end{array}$$

Using the product rules in Exercise 1.2 we can prove the following integration by parts theorem.

Theorem 1.58 (Integration by Parts).

Given two functions $$u,v: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ and $$b,c \in \mathbb{N}_{a}$$ , b < c, we have the integration by parts formulas

$$\displaystyle\begin{array}{rcl} \int _{b}^{c}u(t)\Delta v(t)\Delta t = u(t)v(t)\Big\vert _{ b}^{c} -\int _{ b}^{c}v(\sigma (t))\Delta u(t)\Delta t.& &{}\end{array}$$

(1.26)

$$\displaystyle\begin{array}{rcl} \int _{b}^{c}u(\sigma (t))\Delta v(t)\Delta t = u(t)v(t)\Big\vert _{ b}^{c} -\int _{ b}^{c}v(t)\Delta u(t)\Delta t.& &{}\end{array}$$

(1.27)

Example 1.59.

Evaluate

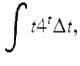
$$\displaystyle{\int t4^{t}\Delta t,}$$

where we consider t4 t for $$t \in \mathbb{N}_{0}.$$ Note that

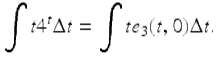
$$\displaystyle{\int t4^{t}\Delta t =\int te_{ 3}(t,0)\Delta t.}$$

To set up integration by parts let

$$\displaystyle{u(t) = t,\quad \Delta v(t) = e_{3}(t,0).}$$

We then use

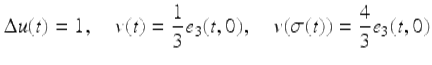
$$\displaystyle{\Delta u(t) = 1,\quad v(t) = \frac{1} {3}e_{3}(t,0),\quad v(\sigma (t)) = \frac{4} {3}e_{3}(t,0)}$$

and the integration by parts formula (1.26) to get

$$\displaystyle\begin{array}{rcl} \int t4^{t}\Delta t& =& \int te_{ 3}(t,0)\Delta t {}\\ & =& \frac{1} {3}te_{3}(t,0) -\frac{4} {3}\int e_{3}(t,0)\Delta t {}\\ & =& \frac{1} {3}te_{3}(t,0) -\frac{4} {9}e_{3}(t,0) + C {}\\ & =& \frac{1} {3}t4^{t} -\frac{4} {9}4^{t} + C. {}\\ \end{array}$$