Math Workout for the GMAT
Part III Content and Strategy Review
Chapter 1 Data Sufficiency 1
Data sufficiency questions give many test takers headaches. Merely figuring out what you’re asked to do can be awkward. You may know the concept a question is testing but still miss it because you are confused by the data sufficiency format.
In this chapter, you’ll decipher what it all means and learn a simple but extremely effective approach for those data sufficiency questions.
WHAT DOES IT ALL MEAN?
The first time you get a data sufficiency question, you will see a screen describing the directions for that type of question. It will say something like this:
Each data sufficiency problem consists of a question and two statements, labeled (1) and (2), which contain certain data. You have to decide whether the data given in the statements are sufficient for answering the question. Using these data and your knowledge of mathematics and everyday facts (such as the number of days in July or the meaning of the word counterclockwise), you must decide whether the data given are sufficient for answering the question and then indicate one of the following answer choices:
· Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient.
· Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient.
· BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
· EACH statement ALONE is sufficient.
· Statements (1) and (2) TOGETHER are NOT sufficient.
You could easily spend a large amount of time trying to understand that confusing morass of instructions. If you do that during the test, you’re throwing away precious minutes that you need to answer the questions. Instead, you should understand the data sufficiency format forward and backward before you ever set foot inside a testing center. So let’s break it apart and see what those directions really mean.
Your mission on a data sufficiency problem is to determine which statement or combination of statements gives you enough information to answer the question. Then you choose the answer choice that matches that combination. The following chart shows you what the answers mean:
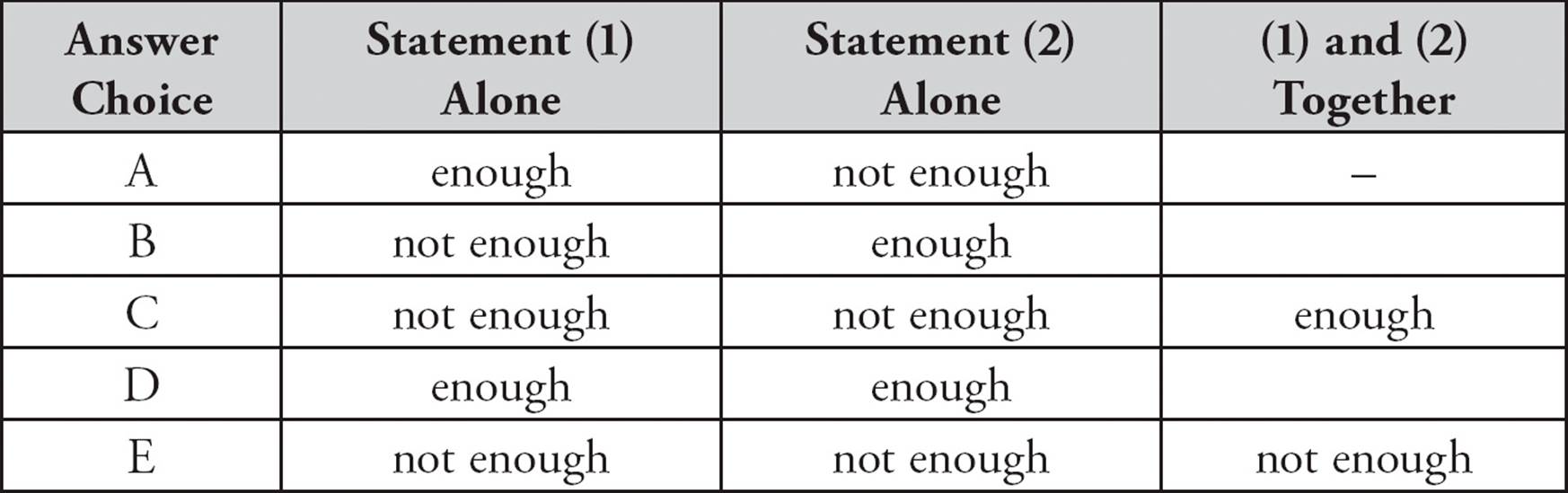
Here’s another way to think about what each answer choice means.
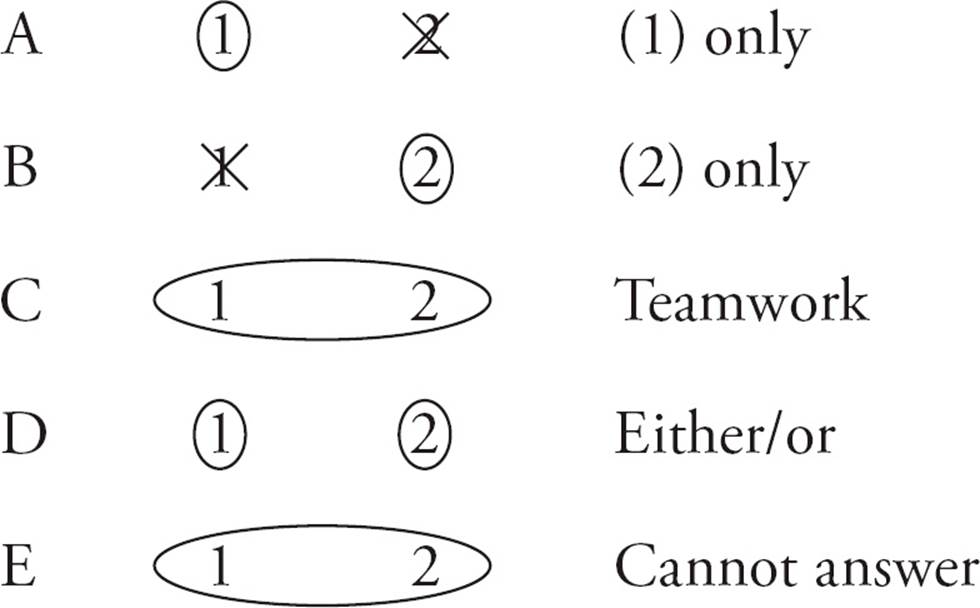
These answer choices are the same for every data sufficiency problem. Memorize the “definition” of each answer choice so that you never need to read the directions or the text of the answer choices.
Note: Since the answers are always the same for each data sufficiency problem, the questions presented later in this book do not supply the answer choices. Practice answering the questions without looking back at the choices.
AD OR BCE
Don’t try to look at both statements at the same time to sort out which answer fits. That way leads to madness. Instead, you should look at one statement at a time, determine whether you can answer the question using the statement, and eliminate the appropriate answer choices. Follow this flowchart:
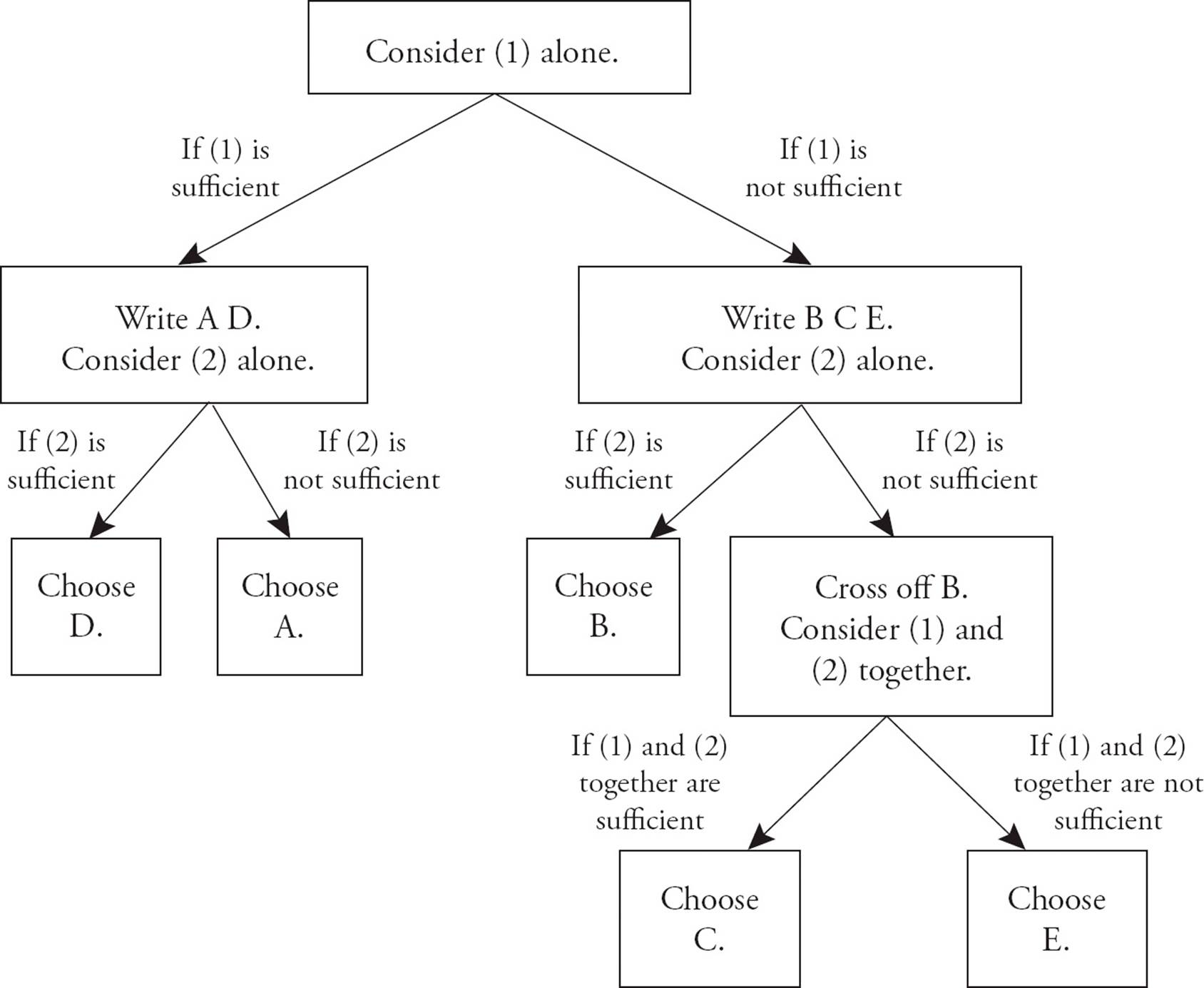
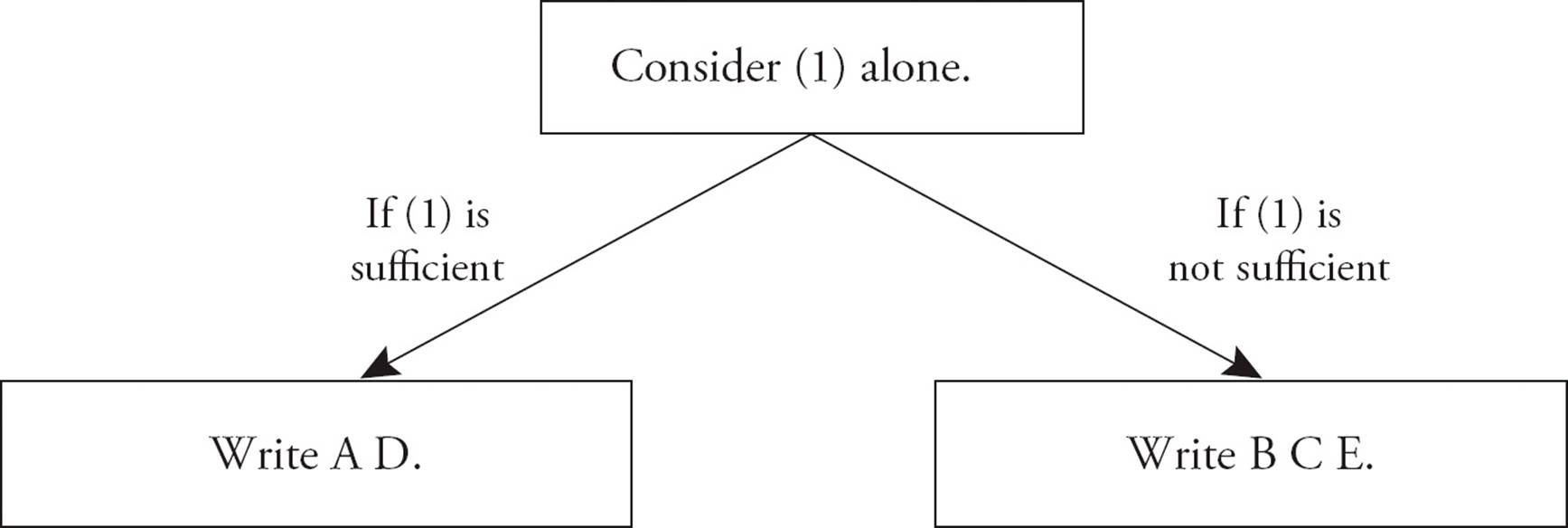
Your first step on any data sufficiency question is to consider Statement (1) alone and narrow your choice to AD or BCE. Do not read Statement (2) yet. If Statement (1) provides enough information to answer the question, then (A) and (D) are the only possible answer choices. If Statement (1) is insufficient, then only (B), (C), and (E) are possible. Based on Statement (1) alone, you will eliminate half of the answer choices.
Next, you will consider Statement (2) alone. It is extremely important that you forget what you saw in Statement (1). Avoid the common mistake of rushing immediately into considering both statements together. Suppose that Statement (1) was sufficient to answer the question, and you are left with (A) and (D) as possible answers. If Statement (2) is not enough (by itself) to answer the question, then (A) must be the answer. If Statement (2) is enough, then (D) is the correct answer.
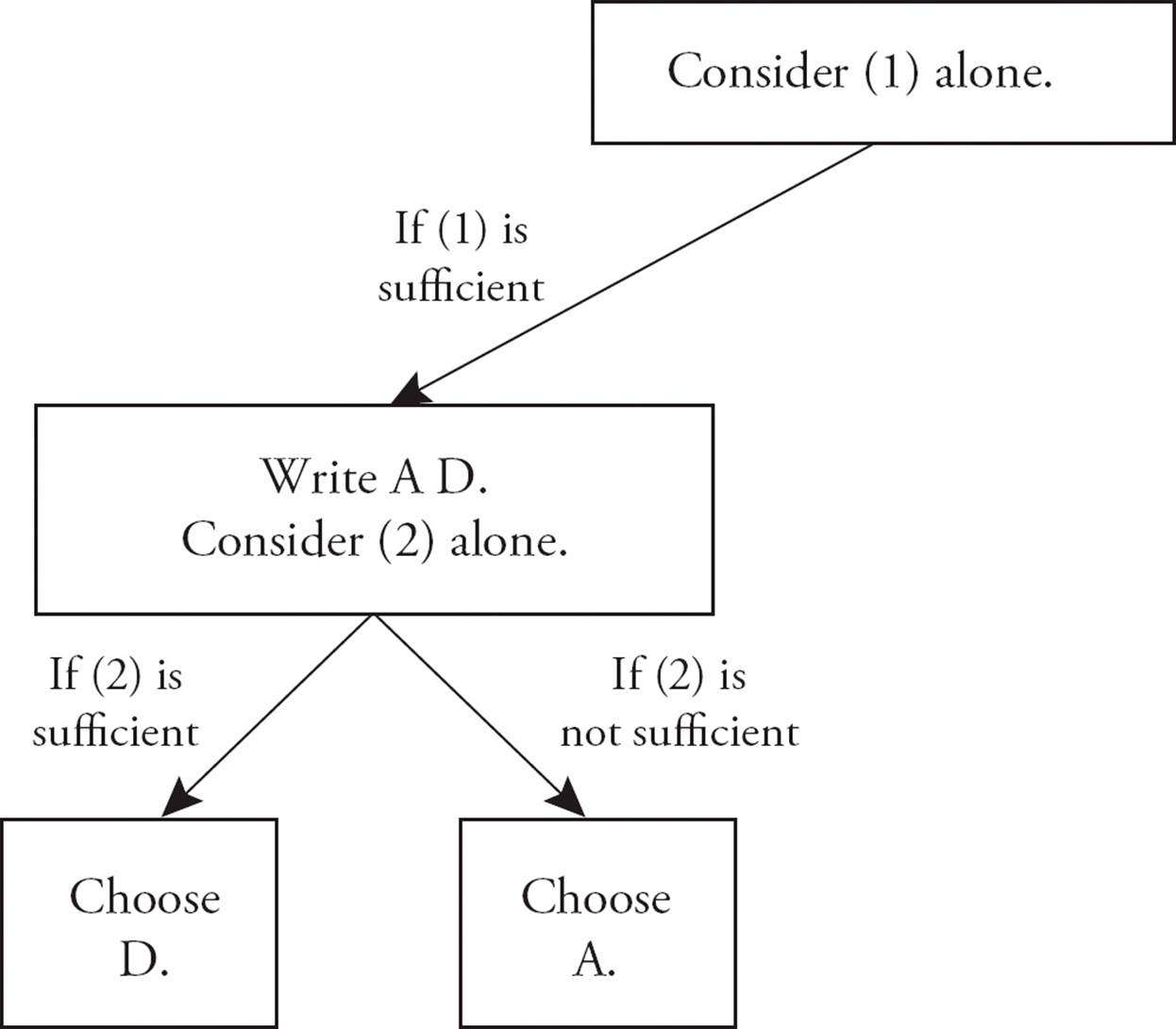
Now, suppose that Statement (1) was not enough, and your initial elimination left you with answers (B), (C), and (E). Again, the next stage is to consider Statement (2) by itself. If it is sufficient to answer the question, then (B) is the correct answer. If not, you must eliminate (B) and then consider both statements together.
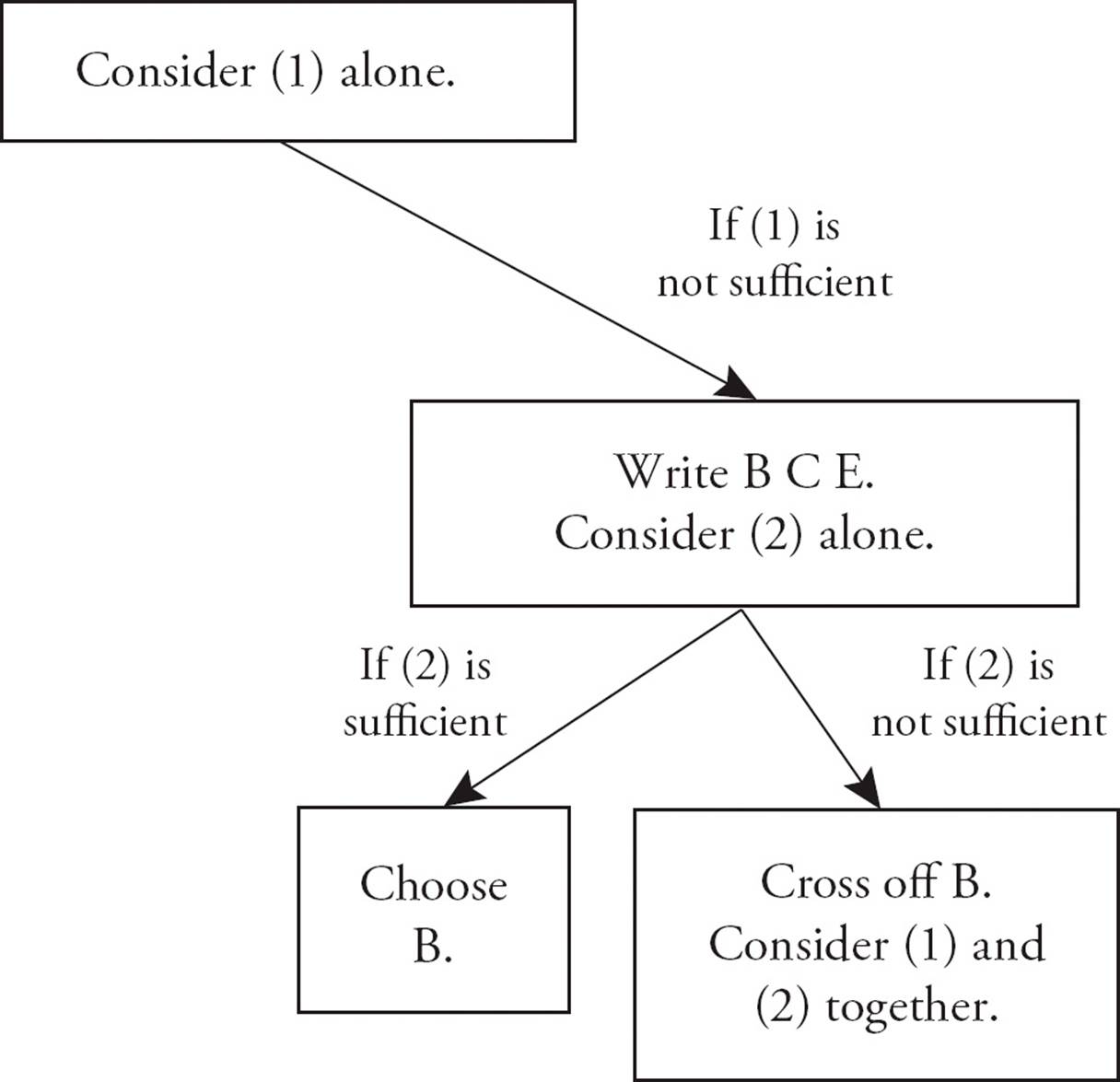
If you are down to (C) and (E) as the remaining answers, then, and only then, will you consider both statements together. At that point, if Statements (1) and (2) combined provide enough information to answer the question, (C) is the correct answer. Otherwise, the question cannot be answered, and you should choose (E).
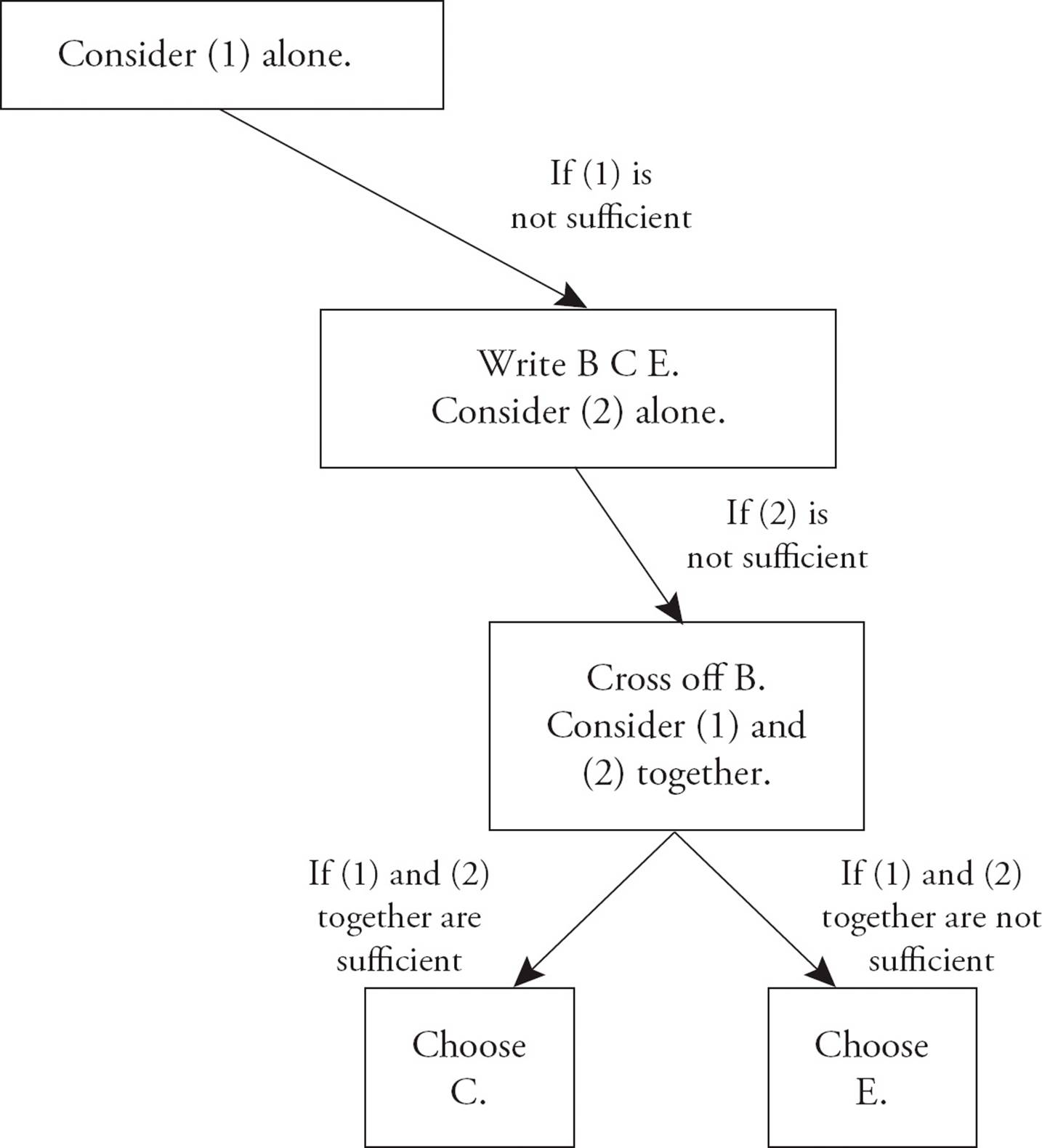
The next examples show this approach in action.
1.How many cookies did Max eat?
(1) Sharon ate 4 cookies, 2 fewer than Max ate.
(2) Max and Sharon together ate 10 cookies.
First, consider Statement (1) alone. This provides enough information to answer the question. Sharon ate 4 cookies, so Max ate 4 + 2 = 6 cookies. Write down “A D” as the answers you have left.
Next, consider Statement (2) alone. This is not enough information. You don’t know how many of the 10 cookies Sharon ate and how many Max ate. You need to forget the information from Statement (1) while you look at Statement (2). You should eliminate (D) because Statement (2) didn’t work, which leaves (A) as the correct answer.
2.How many marbles does Karl have?
(1) Karl has 6 more marbles than Jennifer has.
(2) Jennifer has 8 marbles.
First, consider Statement (1) alone. This isn’t enough information to answer the question. You need to add 6 to something, but you don’t know what that something is. Write down “B C E” as the answers you have left.
Next, consider Statement (2) alone. This isn’t enough either. Forget Statement (1) during this step. Cross off (B) because Statement (2) isn’t enough, and go on to the next step.
Consider Statements (1) and (2) together. Now you can find that Karl has 8 + 6 = 14 marbles. Choose (C).
DRILL 1
The answers can be found on this page.
Remember!
For Data Sufficiency
problems in this book, we
do not supply the answer
choices. The five possible
answer choices are the
same every time.
1.If Mike buys a bicycle and a helmet for a total cost of $315, how much does the helmet cost?
(1) The bicycle costs twice as much as the helmet.
(2) The bicycle costs $210.
2.Carol and Joe went apple picking. Who picked more apples?
(1) Joe picked ![]() as many apples as Carol did.
as many apples as Carol did.
(2) After Carol stopped picking apples, Joe continued to pick apples until he had picked 15 apples.
3.If each child in a group of children received either one or two pieces of candy, how many of the children received two pieces of candy?
(1) Of the children in the group, 25 percent received two pieces of candy.
(2) The children in the group received a total of 15 pieces of candy.
4.If the rents for both Doug’s and Magda’s apartments were increased, which tenant paid the greater dollar increase in rent?
(1) Doug’s rent increased 2 percent.
(2) Magda’s rent increased 8 percent.
5.If x is an integer, is x + 2 even?
(1) x + 3 is an even integer.
(2) x − 2 is an odd integer.
Types of Data Sufficiency
Data Sufficiency questions can be divided into two different categories: Value and Yes/No. While these are covered in more detail in Chapter 8, let’s review these two question formats here. Knowing the differences between these two categories will help you to pick the best way to approach the practice questions in this chapter as well as any data sufficiency questions in subsequent chapters.
Value Data Sufficiency
Value Data Sufficiency questions ask for a value so the answer to the question is a number such as 10. Usually these types of questions are identified by key words such as how many and the value. If the answer to the question is a number or a value of any kind, the question is a value DS question. These types of questions are solved by identifying the information that is given to you in the question stem and the statements and then figuring out what you need to know to get an answer to the question.
Yes/No Data Sufficiency
Yes/No Data Sufficiency questions ask a question that is phrased to require a Yes or No response. For example, a question such as Is x greater than y is a Yes/No data sufficiency question. These types of questions can be tricky to answer. Keep in mind that just because the answer to the question is “No,” that doesn’t mean that the statement is insufficient. Yes/No questions are all about the consistency of the answer to the question. If numbers that satisfy the statement always produce the same answer to the question, whether that answer is “yes” or “no”, the statement is sufficient. But, when some numbers that satisfy the statement produce an answer of “yes” and others produce an answer of “no”, then the statement is insufficient. So, the general approach to these questions is to try several different numbers that satisfy the statement. If even one number exists for which the answer to the question changes, the statement is not sufficient.
ELIMINATE CONFUSION
The data sufficiency format is very confusing. The key to consistent success is following the step-by-step method of eliminating answer choices. Go slowly and carefully as you start practicing this approach; taking the time to master it will pay off with high accuracy, even on the toughest data sufficiency questions.
DON’T FIND THE ANSWER
You usually don’t need to find the actual value asked for in a data sufficiency question. You just need to know whether you could figure it out with the information in the statements. So don’t waste your time solving the problem to come up with the numbers; just setting up the problem will usually be enough.
There is one situation in which you might want to find the number: when you’re not sure whether the problem is actually solvable with the information in the statement. In that case, you should set up the problem and work through it until you are sure, even if you find yourself calculating the solution.
AVOID COMMON MISTAKES
Here are ways to avoid some common mistakes on data sufficiency questions:
· When you consider Statement (2) alone, you must forget what Statement (1) said. Physically covering up the statement with your finger can help. (But be careful about fingerprints on the computer screen!) Otherwise, you may think that Statement (2) provides more information than it really does.
· Don’t rush to consider both statements combined. A common tendency is to read the question and both statements, and then try to juggle all of the information at once. This mistake will lead to choosing (C) too frequently, even though it is wrong. It’s important to consider each of the statements on its own, eliminating answers as you go, before considering them in combination.
· Don’t try to do everything in your head. It is a common error for people to answer data sufficiency questions without writing anything on their scratch paper. That’s a big no-no. Even though you don’t need to calculate an answer, you should write down AD or BCE to help you eliminate. Also, writing down the given pieces of information, setting up equations, and the like often help you determine when you have enough pieces of the puzzle to answer the question.
· As always, read carefully. Data sufficiency questions are notorious for deliberate trickery. Be on the lookout for misleading phrases, and give yourself enough time to read the question slowly and completely.
Comprehensive Data Sufficiency 1 Drill
The answers can be found on this page.
Remember!
For Data Sufficiency problems in this book, we do not supply the answer choices. The five possible answer choices are the same every time.
1.What is the total cost to make 7 long distance telephone calls?
(1) The length of each call was at least 2 minutes.
(2) The rate for long distance calls is $0.32 per minute.
2.If s and t are positive, what is the value of s ?
(1) t = 2.7
(2) s = 3.1t
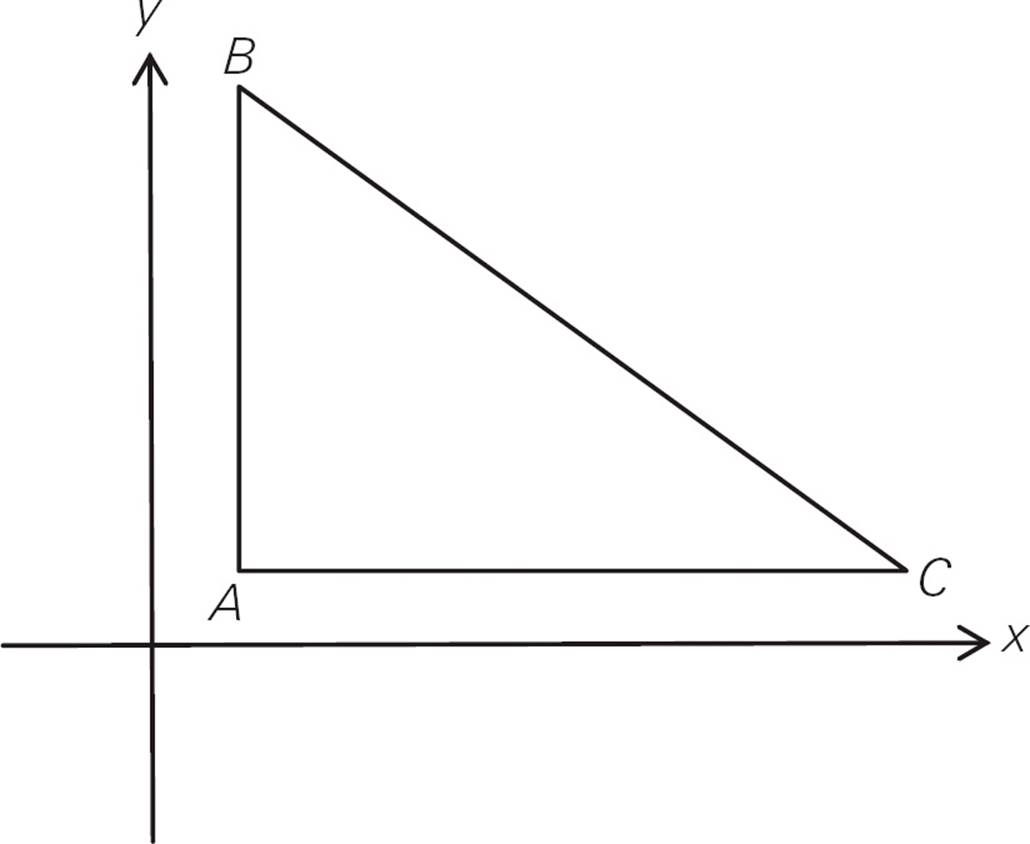
3.In the xy-plane above, is angle BAC greater than 90 degrees?
(1) Points A and B have different x-coordinates.
(2) The measure of angle B is twice the measure of angle C.
4.Of the first three dozen cookies baked at a bake shop on a certain day, ![]() were chocolate chip cookies. If
were chocolate chip cookies. If ![]() of the remaining cookies that were baked that day were chocolate chip cookies, how many chocolate chip cookies were baked that day?
of the remaining cookies that were baked that day were chocolate chip cookies, how many chocolate chip cookies were baked that day?
(1) The bakery made five dozen cookies that day.
(2) Of all the cookies made that day, ![]() were chocolate chip.
were chocolate chip.
5.The usual price of a bagel was reduced during a sale. How much money could be saved by purchasing 10 bagels at the sale price rather than at the usual price?
(1) The usual price for a bagel is $0.50 per bagel.
(2) The sale price for a bagel is $0.40 per bagel.
6.Does 3r + s = 276 ?
(1) r – s = 8
(2) 5r = 13s
7.If a total of 30 puppies is displayed in the two windows of a pet store, how many of the puppies are female?
(1) ![]() of the puppies in the left window are male.
of the puppies in the left window are male.
(2) ![]() of the puppies in the right window are female.
of the puppies in the right window are female.
8.If f denotes a decimal, is f < 0.5 ?
(1) When f is squared, the result is less than 0.5.
(2) When f is rounded to the nearest integer, the result is 1.
9.Jim and Nancy each provide the same service at a different original price. If both Jim and Nancy discount their original price, is Nancy’s discount price less than Jim’s discount price?
(1) Jim’s discount price is 20 percent less than his original price and Nancy’s discount price is 30 percent less than her original price.
(2) Jim’s discount price is $10 less than his original price and Nancy’s discount price is $12 less than her original price.
10.Is abc = 1 ?
(1) a = ![]()
(2) b = ![]()
11.If a certain parking lot contains 40 motor vehicles, how many of the vehicles are red trucks?
(1) Of the motor vehicles in the parking lot, 20 percent are painted red.
(2) Of the motor vehicles in the parking lot, 15 are trucks.
12.Bruce, John, Linda, and Mark stand, in that order, in a straight line. If Linda stands 7 feet away from Mark, what is the distance from Bruce to John?
(1) Bruce stands 7 feet away from Linda.
(2) John stands 11 feet away from Mark.
13.Is the number of workers required to create w1 widgets at r1 widgets per minute less than the number of workers required to create w2 widgets at r2 widgets per minute?
(1) w1 is 20 less than w2.
(2) r1 is 20 less than r2.
14.At a certain school, is the number of biology students greater than the number of chemistry students?
(1) Of the biology students, 30 percent are also chemistry students.
(2) Of the chemistry students, 40 percent are also biology students.
15.Mike bought a computer system for $4,000 and later sold it. For what price did Mike sell the computer system?
(1) Mike sold the computer system for 60% of the price he paid for it.
(2) Mike advertised the computer system in a newspaper at a price of $3,000, which was 25% more than the price for which he actually sold it.
16.How old, rounded to the nearest year, was Jim in May 1989 ?
(1) Jim’s friend Steve, who is exactly 2 years older than Jim, turned 25 years old in 1972.
(2) In March 1982, Jim turned 33 years old.
17.Of the 3,000 cars manufactured in Factory Q last year, how many were still in operation at the end of the year?
(1) Of all of the cars manufactured in Factory Q, 60% were still in operation at the end of last year.
(2) A total of 48,000 cars manufactured in Factory Q were still in operation at the end of last year.
18.Is q < 0 ?
(1) 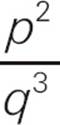 > 0
> 0
(2) q2 − 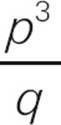 < 0
< 0
19.If a and b are integers, is ab odd?
(1) b = a + 2
(2) ![]() is an odd integer.
is an odd integer.

Challenge!
Take a crack at this high-
level GMAT question.
20.A terminating decimal is a number with a finite number of nonzero digits. For example, 35, 14.07, and 5.341 are three terminating decimals. For positive integers p and q, when ![]() is expressed as a decimal, is
is expressed as a decimal, is ![]() a terminating decimal?
a terminating decimal?
(1) p is the sum of three consecutive odd multiples of 5.
(2) 2q2 + 144 = 36q
ANSWERS AND EXPLANATIONS
Drill 1
1.DStart with Statement (1). Since the bicycle costs twice as much as the helmet and the helmet and bicycle together cost $315, the only possible prices are $105 for the helmet and $210 for the bicycle. Therefore, Statement (1) is sufficient so write down AD as the possible answer choices. Next, look at Statement (2). If the bicycle costs $210, just subtract that number from $315 to get the price of the helmet. Statement (2) is also sufficient to answer the question so select choice (D).
2.AStart with Statement (1). This statement doesn’t give any information about the number of apples picked by either person, but does provide a relationship between the two. Since Joe picked fewer apples than Carol did, Statement (1) is sufficient to answer the question. So write down AD. Next look at Statement (2). This statement gives information about how long it took for Joe to pick his apples, but gives no information about how many he picked. Since he could have picked more or fewer than Carol, this statement is insufficient, so choose choice (A).
3.CStart with Statement (1). Without knowing the total number of children, the number of children who received two pieces of candy cannot be found from the percentage of the children who received two pieces of candy. Write down choices BCE for the remaining answers. Next, look at Statement (2). This statement gives the total number of pieces handed out to the children, but gives no information about how many children received one versus two pieces of candy. Maybe 1 child received 2 pieces and 13 children received 1 piece each. Maybe 7 children received 2 pieces each and 1 child received 1 piece. Since there is more than one possible answer, Statement (2) is insufficient so eliminate choice (B). Now, try both statements together. If there are x children, then 75% of x receive 1 piece and 25% of x receive 2 pieces. Given that the total number of pieces is 15, set up the equation: (0.75 × 1 × x) + (0.25 × 2 × x) = 15. Since this is a solvable equation and it would reveal an answer to the question, both statements together are sufficient so choose choice (C).
4.EStart with Statement (1). This statement only gives information about the percentage increase in Doug’s rent but no information about either Magda’s rent increase or the starting rent for either tenant. This statement is insufficient so write down choices BCE. Next, look at Statement (2). This statement only gives information about the percentage increase in Magda’s rent, but no information about either Doug’s rent increase or the starting rents for either tenant. Statement (2) is insufficient, so eliminate choice (B). Next, look at both statements together. The percent by which Magda’s rent increases is greater than that of Doug’s rent increase, but since the problem never provides any information about the starting rents, it is impossible to answer the question. Both statements together are insufficient, so select choice (E).
5.DThis is a “Yes/No” data sufficiency question, so begin by assessing the question that needs to be answered. The question is whether x + 2 is even. Start working with the statements to see if there is a consistent answer, which can be either “Yes” or “No,” to this question.
To evaluate Statement (1), that x + 3 is an even integer, plug in a number for x that satisfies the statement. Try x = 3. Since 3 + 3 = 6, Statement (1) is satisfied. Next, answer the question with x = 3. Since 3 + 2 = 5, the answer to the question is “No.” Next, find another number that satisfies the statement such as x = 5. This number also produces an answer of “No” to the question. In fact, for any number plus three to equal an even integer, x must be an odd integer. Since any odd integer plus 2 equals an odd integer, the answer to the question is always “No” when Statement (1) is satisfied. Therefore, Statement (1) is sufficient. Write down AD as the possible remaining answer choices and evaluate Statement (2).
To evaluate Statement (2), that x − 2 is an odd integer, plug in a number for x that satisfies the statement. Try x = 3 again. Since 3 − 2 = 1, Statement (2) is satisfied. Since 3 + 2 = 5, the answer to the question is “No.” Next, try another number that satisfies the statement such as x = 5, which also produces an answer of “No” to the question. In fact, for any number minus 2 to equal an odd integer, x must be an odd integer. As with Statement (1), since x is always an odd integer to satisfy Statement (2), x + 2 is always odd. Again, the answer to the question “is x+ 2 even” is always “No” for Statement (2) and the statement is sufficient. Since both statements are sufficient, the correct answer is (D).
Comprehensive Data Sufficiency 1 Drill
1.EStart with Statement (1). Since the question asks about the cost to make the phone calls and this statement gives no information about how much the calls cost, the statement is insufficient so write down choices BCE for the remaining possible answer choices. Look at Statement (2). Combined, the statements give information about the cost per minute and the minimum amount of time each call lasted. However, since no information is given about the exact total amount of time the calls lasted, both statements combined are insufficient. Select choice (E).
2.CStart with Statement (1). Since the question asks for the value of s and this statement only provides information about t, Statement (1) is insufficient. Write down choices BCE. Look at Statement (2). While this statement gives an equation for s, the equation cannot be solved because there is no information provided about t. Statement (2) is insufficient so eliminate choice (B). Look at Statements (1) and (2) combined. The value of t is given in Statement (1) so put t = 2.7 into the equation from Statement (2) to get s = (3.1)(2.7). Since it is now possible to solve for s, the correct answer is (C).
3.EThis is a “Yes/No” data sufficiency question, so plug in numbers to try and determine whether the answer to the question “is angle BAC greater than 90 degrees” is always “Yes” or “No.” If the x-coordinate of point A is 3 and the x-coordinate of point B is 4, then angle BAC is less than 90 degrees and the answer to the question is “No.” However, if the x-coordinate of point A is 3 and the x-coordinate of point B is 2, then angle BAC is greater than 90 degrees and the answer to the question is “Yes.” Since there is both a “Yes” and a “No” answer to this question, Statement (1) is not sufficient. Write down BCE as the remaining possible answer choices.
Statement (2) states that the measure of angle ABC is twice the measure of angle BCA. Plug In again. If angle BCA equals 20°, then angle ABC is 40°, and angle BAC is the remainder. Since the sum of the degree measures of the angles in a triangle is 180°, angle BAC is equal to 180° – (40° + 20°) = 120°. If BAC is 120°, then the answer to the question “is angle BAC greater than 90 degrees” is “Yes.” However, if angle BCA equals 50°, then angle ABC is 100° and the value of BAC is 180° – (100° + 50°) = 30°. If BAC is 30° then the answer to the question is “No.” Since there is both a “Yes” and a “No” answer, Statement (2) is not sufficient. Eliminate choice (B).
Now, evaluate both statements together. Try to recycle any numbers already used that could satisfy both statements. The values when angle BCA equals 20°, angle ABC is 40°, and angle BAC equals 120° satisfy both statements. In this case, the x-coordinate of point B is less than the x-coordinate of point A. The answer to the question is “Yes.” Now see if there is a way to make the answer “No” by creating values that satisfy both statements and make angle BAC less than 90°. Recycle the second set of numbers used for the second statement. If angle BCAequals 50°, angle ABC is 100° and angle BAC is 30°. In this case, the x-coordinate of point B is greater than the x-coordinate of point A. Since the answer to the question is now “No” and the answer previously was “Yes”, both statements combined are not sufficient to answer the question, so the correct answer is choice (E).
4.DStart with Statement (1). If 5 dozen cookies were made that day, and one third of the first 36 cookies are chocolate chip cookies, which is 12 cookies, that leaves another 24 cookies that were made. Since half of those 24 cookies were chocolate chip, there are 12 + 12 = 24 chocolate chip cookies. Statement (1) is sufficient to answer the question so write down AD. Look at Statement (2). This statement provides that two-fifths of the cookies made were chocolate chip so set up the equation ![]() x+
x+![]() y=
y= ![]() (x + y), in which x is the first set of cookies (3 dozen), and yis the number of remaining cookies. Since x = 36, plug that into the equation and solve for y. The total number of chocolate chip cookies is then
(x + y), in which x is the first set of cookies (3 dozen), and yis the number of remaining cookies. Since x = 36, plug that into the equation and solve for y. The total number of chocolate chip cookies is then ![]() (x + y). Statement (2) is also sufficient so select choice (D).
(x + y). Statement (2) is also sufficient so select choice (D).
5.CStart with Statement (1). This statement provides the usual price, but gives no information about the sale price. Therefore, the question cannot be answered and Statement (1) is insufficient. Write down choices BCE. Look at Statement (2). This statement provides the sale price, but gives no information about the usual price. Therefore, the question cannot be answered so eliminate choice (B). Look at Statements (1) and (2) together. Combined, the statements give information about the usual price and the sale price so it is possible to answer the question. The correct answer is choice (C).
6.CThis is a “Yes/No” data sufficiency question. Begin by assessing the question. Start by rewriting the equation in the question stem using common bases, to find that 3r + s = (33)6 = 318. Since the bases are the same, the exponent expressions can be set as equal. So the question is really asking “Is r + s = 18?” Now evaluate the statements to see if the information is sufficient to answer the question.
To evaluate Statement (1), r – s = 8, plug in numbers for r and s. If r = 13 and s = 5, then the statement is satisfied. These numbers also produce a “Yes” answer to the question because 13 + 5 = 18. Now, see if there is a way to get a “No” answer. If r = 9 and s = 1, then the statement is still satisfied but the answer to the question “Is r + s = 18?” is now “No.” Statement (1) is insufficient, so write down BCE as the possible answer choices.
Statement (2) is 5r = 13s. Plug in again. If r = 13 and s = 5, then the statement is satisfied and the answer to the question Is r + s = 18?” is “Yes.” Now, see if there is a way to get a “No” answer. If r = 0 and s = 0, then the answer to the question is now “No.” Eliminate choice (B).
Look at both statements together and recycle any values that were already used. If r = 13 and s = 5, then both statements are satisfied and the answer to the question “Is r + s = 18?” is “Yes.” Since there is no other possible combination that satisfies both statements, the correct answer is (C).
7.EStart with Statement (1). This statement provides the fraction of male puppies that are in the left window and can be used to determine the fraction of the female puppies in the left window. However, how many of the 30 puppies that are in the left window is unknown. This statement is insufficient, so write down choices BCE. Look at Statement (2). This statement presents the same problem as Statement (1) but in the other window. Statement (2) is insufficient so eliminate choice (B). Look at Statements (1) and (2) together. Although you know the male-to-female proportion in each window, you don’t know how many puppies are in each window. If there are 24 puppies in the left window and 6 in the right, then there are 6 + 2 = 8 female puppies. If there are 12 puppies in the left window and 18 puppies in the right, then there are 3 + 6 = 9 female puppies. Since there are two possible answers, the statements combined are insufficient and the correct answer is (E).
8.BThis is a Yes/No data sufficiency question. The question wants to know whether f < 0.5 given that f is a decimal. Statement (1) states that when f is squared, the result is less than 0.5. Plug in a number for f that satisfies that statement. If f = 0.4, then the result when f is squared is 0.16, which is less than 0.5, so the statement is satisfied. The answer to the question is f < 0.5 is then “Yes” as f = 0.4. Try to find a number for f that gives a “No” answer. If f = 0.6 then, when squared, the result is 0.36. This is less than 0.5, so the statement is satisfied, but the answer to the question is f < 0.5 is now “No.” Therefore, Statement (1) is not sufficient, so write down BCE. Statement (2) provides that when f is rounded to the nearest integer, the result is 1. Plug in again. If f = 0.6 then the statement is satisfied. The answer to the question is f < 0.5 is now “No.” Since any decimal that is rounded to 1 has to be greater than or equal to 0.5, the answer to the question is f < 0.5 is always “No.” Therefore, Statement (2) is sufficient and the answer is (B).
9.CThis is a Yes/No data sufficiency question so evaluate both statements by plugging in numbers but remember that the original prices for Nancy and Jim cannot be the same. Look at Statement (1). Plug in a number for the original price for Jim’s service. If Jim’s original price is $100, then his discount price is 80% of 100, or $80. If Nancy’s original price is $110, then her discount price is 70% of $110, or $77. In this scenario, Nancy’s discount price is less than Jim’s discount price, so the answer to the question is “Yes.” Now see if there are different numbers to plug in to make the answer to the question “No.” If Jim’s original price is $10, then his discounted price is $8. If Nancy’s original price is $100, then her discounted price is $70. The answer to the question is now “No”, which means that Statement (1) is insufficient. Write down BCE.
Look at Statement (2) and try to reuse numbers from Statement (1). If Jim’s original price is $100, then his discounted price is $90. If Nancy’s original price is $110, then her discounted price is $98. In this case, Nancy’s price is not less than Jim’s discounted price and the answer to the question is “No.” Now see if there is a way to make the answer “Yes.” If Jim’s original price is $110, then his discounted price is $100. If Nancy’s original price is $100, then her discounted price is $88. In this case, Nancy’s price is less than Jim’s discounted price and the answer to the question is “Yes.” Since there is a “Yes” and a “No” answer, Statement (2) is not sufficient, so eliminate choice (B).
Now look at the statements together. These statements together provide a percent discount and a value for the discount. With these two pieces of information, the value of the original and discounted price could be determined. So without doing any of the work, the answer is choice (C). However, it never hurts to double check. If Jim’s discount price is 20% less than the original price and also $10 less than the original price, then $10 is 20% of the original price. So the original price of Jim’s service is $50 and the discounted price is $40. If Nancy’s discount price is 30% less than the original price and also $12 less than the original price, then $12 is 30% of the original price. Therefore, the original price of Nancy’s service is $40 and the discounted price is $28. Since there are no other options, the two statements together are sufficient and the answer is (C).
10.EThis is a Yes/No data sufficiency question. Evaluate the statements one at a time by Plugging In. Look at Statement (1). First, simplify this equation by putting the variables on the same side to find that ab = 1. If a = 2, b = ![]() , and c = 2, the statement is satisfied but the answer to the question is “No”. However, if a = 2, b =
, and c = 2, the statement is satisfied but the answer to the question is “No”. However, if a = 2, b = ![]() , and c = 1, the statement is also satisfied and the answer to the question is “Yes”. Statement (1) is insufficient, so write down BCE. Next, simplify Statement (2) to find that bc = 1. Again, Plug In. If a = 2, b =
, and c = 1, the statement is also satisfied and the answer to the question is “Yes”. Statement (1) is insufficient, so write down BCE. Next, simplify Statement (2) to find that bc = 1. Again, Plug In. If a = 2, b = ![]() , and c = 2, the statement is satisfied but the answer to the question is “No”. However, if a = 1, b =
, and c = 2, the statement is satisfied but the answer to the question is “No”. However, if a = 1, b = ![]() , and c = 2, the statement is also satisfied and the answer to the question is “Yes”. Statement (2) is insufficient so eliminate (B). Now look at the statements together. Use the simplified equations to make the statements easier to work with. Statement (1) says that ab = 1, so plug 1 for both a and b. Statement (2) says that bc = 1. Since b is already 1, c equals 1 as well. Therefore, abc = (1)(1)(1) = 1. The answer to the question is “Yes.” Now see if there are other number to plug in that could make the answer “No.” If a = −1 and b = −1, then Statement (1) is satisfied as (−1)(−1) = 1. If b = −1 then to satisfy Statement (2) c must also equal −1. Both statements are satisfied but now abc = (−1)(−1)(−1) = −1 and the answer to the question is “No.” Since there is a “Yes” answer and a “No” answer, the statements together are not sufficient, so eliminate (C). The correct answer is (E).
, and c = 2, the statement is also satisfied and the answer to the question is “Yes”. Statement (2) is insufficient so eliminate (B). Now look at the statements together. Use the simplified equations to make the statements easier to work with. Statement (1) says that ab = 1, so plug 1 for both a and b. Statement (2) says that bc = 1. Since b is already 1, c equals 1 as well. Therefore, abc = (1)(1)(1) = 1. The answer to the question is “Yes.” Now see if there are other number to plug in that could make the answer “No.” If a = −1 and b = −1, then Statement (1) is satisfied as (−1)(−1) = 1. If b = −1 then to satisfy Statement (2) c must also equal −1. Both statements are satisfied but now abc = (−1)(−1)(−1) = −1 and the answer to the question is “No.” Since there is a “Yes” answer and a “No” answer, the statements together are not sufficient, so eliminate (C). The correct answer is (E).
11.EStart with Statement (1). The statement says that overall 20% of the motor vehicles are painted red, but this does not give any information about how many of those red vehicles are trucks. Since the question cannot be answered, Statement (1) is insufficient so write down choices BCE. Look at Statement (2). From this statement, there are 15 trucks, but there is no information about the number that are painted red. Statement (2) is insufficient so eliminate choice (B). Look at Statements (1) and (2) together. The statements combined give that there are 15 trucks and 20% of all motor vehicles are painted red, but does not give any information about what percentage of the trucks are painted red. It is possible that all the trucks are painted red. It is also possible that none of the trucks are painted red and all the red motor vehicles are non-trucks. Both statements combined cannot answer the question so the correct answer is choice (E).
12.CStart by drawing a picture. It should look something like this.

Now, look at Statement (1). From the question, the distance from L to M is 7 feet. Statement (1) gives that B to J plus J to L is 7 feet. However, since it is impossible to determine how much of the 7 feet is made up of the distance from B to J the question cannot be answered so write down BCE. Look at Statement (2). Statement (2) says that the distance from J to M is 11 feet, which means the distance from J to L is 4 feet because the question stem states that L to M is 7 feet. However, this gives no information about how far B is away from the others, so Statement (2) is insufficient. Eliminate choice (B). Look at Statements (1) and (2) together. From the question, the distance from L to M is 7 feet. Statement (1) gives that the distance from B to J plus J to L is 7 feet. Statement (2) gives that the distance from J to L is 4 feet. So, the distance from B to J is 3 feet. This answers the question so the correct answer is (C).
13.EThis is a Yes/No data sufficiency question. Evaluate one statement at a time to attempt to produce both a “Yes” and a “No” answer by plugging in different numbers. This is a rate problem, so to evaluate it both values of w and r must be determined. Statement (1) provides a relationship between w1 and w2 but provides no information about the relationship between r1 and r2. Therefore, Statement (1) is insufficient. Write down BCE. Statement (2) is also insufficient for the same reason that Statement (1) is insufficient, so eliminate choice (B). Now evaluate both statements together. Plug in numbers that satisfy both statements. If w1 = 20 and r1 = 20, then according to the statements, w2 = 40 and r2 = 40. The rate at which w1 widgets are created is 20 widgets per minute, so the total time to create the widgets is 1 minute. The rate at which w2 widgets are created is also 1 minute as 40 widgets are created at 40 widgets per minute. Since the two values are equal, the answer to the question is “No.” See if the answer can be “Yes” by plugging in different numbers. If w1 = 5 and r1 = 10, then the rate to produce w1 widgets is 5 widgets at 10 widgets per minute which is 0.5 minutes to create 5 widgets. To satisfy the statements, w2 = 25 and r2 = 30, which means that the rate to produce w2 widgets is 25 widgets at 30 widgets per minute. The exact value of the rate for w2 widgets is irrelevant, as the rate is greater than 0.5 minutes. The answer to the question is now “Yes.” Since there is a “Yes” and a “No” answer, eliminate choice (C). The correct answer is choice (E).
14.CThe question stem itself gives very little information to work with other than the fact that there are two types of students: biology and chemistry. For convenience use the variables b and c to represent these two types of students. Now consider Statement (1). This statement is really saying that some number of students take both biology and chemistry. Since the statement says that a portion of the biology students are also chemistry students, Plug In a value for b. If b = 40, and 30% of b is 12, then 12 students take both biology and chemistry. Note, however, that the number of students who only take chemistry cannot be determined from this statement. When b = 40, if c = 20, the answer to the question is “Yes”. But, if c = 60, the answer to the question is “No.” So, Statement (1) is insufficient. Write down BCE as the remaining possible answers.
Now consider Statement (2). This statement is really saying that some students take both biology and chemistry. But, similar to Statement (1), this statement does not provide the number of students who only take biology. So Statement (2) is insufficient. Eliminate answer choice (B).
Now combine the two statements. Both statements give an equation for the number of students who take both biology and chemistry. If 30% of biology students take chemistry and 40% of chemistry students take biology, then the number of students who take both can be represented by the equation 0.3(b) = 0.4(c). Now plug in for one of the variables. For instance, make b = 40 and plug that into the equation, to yield 0.3(40) = 0.4c which results in 12 = 0.4c. Solve for c by dividing both sides by 0.4 and c = 30. Consequently, the answer to the question is “Yes” as there are more biology students than there are chemistry students. To be sure, check again with another number. This time, try to plug in a number for c first. If c = 100, then 0.3(b) = 0.4(100) and this yields 0.3(b) = 40. Solve for b to find that b = 133.33. So, bis still greater. The answer to the question is always going to be that b is greater. Because the two statements together are sufficient to determine there are more biology students than chemistry students, the correct response is answer (C).
15.DStart with Statement (1). The statement says that Mike sold the system for 60% of what he paid for it. The question stem says that he paid $4,000 for the system, so Statement (1) is sufficient to answer the question. Write down AD. Look at Statement (2). Statement (2) says that $3,000 is 25% more than the actual selling price. Since the sale price can be found, Statement (2) is sufficient and choice (D) is the correct answer.
16.BStart with Statement (1). Because Steve turned 25 in 1972, it is possible to determine that Jim turned 23 in 1972. So Jim must have turned 40 in 1989, but since the question gives no information about whether his birthday was before or after May, he could be either 39 or 40. Statement (1) is insufficient so write down BCE. Look at Statement (2). If Jim turned 33 in March 1982, then he turned 40 in March 1989 and he would still be 40 in May. Statement (2) is sufficient so select (B).
17.EStart with Statement (1). The 60% of cars given in Statement (1) refers to all cars ever manufactured in Factory Q, not just those made last year. Statement (1) is insufficient so write down BCE. Look at Statement (2). This statement still does not give any information about how many of those cars are from last year, so Statement (2) is insufficient. Look at Statements (1) and (2) together. The combined statements still do not give any information about the cars from last year, so the statements together are not sufficient to answer the question and the correct answer is (E).
18.AThe question stem asks a Yes or No question, which indicates that Plugging In is a good strategy to solve this problem. For Statement (1), plug in numbers that satisfy the statement. Let p = 4 and q = 2. Since 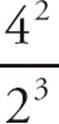 = 2 > 0, this satisfies Statement (1). Since q is positive, the answer to the question is “No.” Now, attempt to get a “Yes” answer. Try p = 4 and q = −2. However, since
= 2 > 0, this satisfies Statement (1). Since q is positive, the answer to the question is “No.” Now, attempt to get a “Yes” answer. Try p = 4 and q = −2. However, since 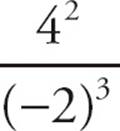 = −2 < 0, this does not satisfy Statement (1), so these numbers cannot be used to answer the question. There are no negative values of q that satisfy this statement. Therefore, the answer to the question is always “No,” and Statement (1) is sufficient. Write down AD as the possible answers.
= −2 < 0, this does not satisfy Statement (1), so these numbers cannot be used to answer the question. There are no negative values of q that satisfy this statement. Therefore, the answer to the question is always “No,” and Statement (1) is sufficient. Write down AD as the possible answers.
Now plug in numbers that satisfy Statement (2). Let p = 4 and q = 2. Since 22−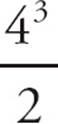 = 4−32 = −28 < 0, this satisfies Statement (2). Since q > 0, the answer to the question is “No.” Now, attempt to get a “Yes” answer. Try p = −4 and q = −2. Since (−2)2 −
= 4−32 = −28 < 0, this satisfies Statement (2). Since q > 0, the answer to the question is “No.” Now, attempt to get a “Yes” answer. Try p = −4 and q = −2. Since (−2)2 − 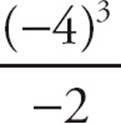 = 4 − 32 = −28 < 0, this satisfies Statement (2). Since q is negative, the answer to the question is “Yes.” Since the answers are different, Statement (2) is insufficient. Since only Statement (1) is sufficient alone, the correct answer is (A).
= 4 − 32 = −28 < 0, this satisfies Statement (2). Since q is negative, the answer to the question is “Yes.” Since the answers are different, Statement (2) is insufficient. Since only Statement (1) is sufficient alone, the correct answer is (A).
19.CPlug In to solve this data sufficiency question. Begin with Statement (1). If b = a + 2, then plug in a number for a, such as 2. If a = 2, then b = 4. Now answer the question “Is ab odd?” Since 4 × 2 = 8, ab is not odd, so the answer is “No”. Now try to make the answer “Yes” by trying different integers for a. If a = 1 then b = 3 and then ab = 3 × 1 = 3. Now the answer to the question is “Yes”. Since one situation produced a “No” answer and another created a “Yes” answer, Statement (1) is not sufficient. Write down BCE for the remaining possible answer choices. Statement (2) says that ![]() is an odd integer, so plug in again. If b = 3 and a = 1, then
is an odd integer, so plug in again. If b = 3 and a = 1, then ![]() =
= ![]() = 3, which satisfies the statement. Now answer the question “Is ab odd?” Since 3 × 1 = 3, ab is odd, so the answer is “Yes.” Now try to make the answer to the question “No.” First satisfy Statement (2) with different integers. If a = 2 and b = 6, then
= 3, which satisfies the statement. Now answer the question “Is ab odd?” Since 3 × 1 = 3, ab is odd, so the answer is “Yes.” Now try to make the answer to the question “No.” First satisfy Statement (2) with different integers. If a = 2 and b = 6, then ![]() =
= ![]() = 3, which is odd, so Statement (2) is satisfied. Now answer the question “Is ab odd?” Since 2 × 6 = 12, the answer is now “No.” Since one situation produced a “No” answer and another created a “Yes” answer, Statement (2) is not sufficient, so eliminate (B).
= 3, which is odd, so Statement (2) is satisfied. Now answer the question “Is ab odd?” Since 2 × 6 = 12, the answer is now “No.” Since one situation produced a “No” answer and another created a “Yes” answer, Statement (2) is not sufficient, so eliminate (B).
Now combine the statements. Recycle any numbers that have already been used that satisfy both statements. If a = 1 and b = 3, then both Statements (1) and (2) are satisfied and the answer to the question, “Is ab odd?” is “Yes.” Now see if there is a pair of integers that satisfy both statements that make the answer “No.” The only other set of integers that satisfy both statements is a = −1 and b = 1. Since −1 × 1 = −1, the answer to the question “Is ab odd?” is always going to be “Yes”. Since both statements together are sufficient to answer the question, the correct answer is (C).
20.CSince this is a Yes/No question, Plug In. Find a number that satisfies Statement (1), which states that p is the sum of three consecutive odd multiples of 5. Try 5 + 15 + 25 = 45. If q = 100, then ![]() =
= 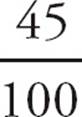 = 0.45, which is a terminating decimal. Therefore, the answer to the question is “Yes.” Now, try to get a “No” answer. If q = 27, then
= 0.45, which is a terminating decimal. Therefore, the answer to the question is “Yes.” Now, try to get a “No” answer. If q = 27, then ![]() =
= 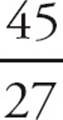 =
= ![]() =
= ![]() , which is not a terminating decimal. Therefore, the answer to the question is “No.” Since it is possible to get a “Yes” and a “No” answer to the question, Statement (1) is insufficient. Write down BCE as the remaining possible answer choices.
, which is not a terminating decimal. Therefore, the answer to the question is “No.” Since it is possible to get a “Yes” and a “No” answer to the question, Statement (1) is insufficient. Write down BCE as the remaining possible answer choices.
Now look at Statement (2), which gives a solvable quadratic. Get one side equal to 0, so subtract 36q from both sides to get 2q2 − 36q + 144 = 0. Next, divide every term by 2 to get q2 − 18q + 72 = 0. Now factor the left side to get (q − 6)(q − 12) = 0. Set both factors equal to 0 to find that q = 6 or q = 12. Now, use one of those values and plug in for p. If p = 1 and q = 6, then ![]() =
= ![]() =
= ![]() , which is not a terminating decimal, so the answer is “No.” If p = 3 and q = 6, then
, which is not a terminating decimal, so the answer is “No.” If p = 3 and q = 6, then ![]() =
= ![]() = 0.5, which is a terminating decimal, so the answer is “Yes.” Since there is both a “Yes” and a “No” answer to the question, Statement (2) is not sufficient. Eliminate (B).
= 0.5, which is a terminating decimal, so the answer is “Yes.” Since there is both a “Yes” and a “No” answer to the question, Statement (2) is not sufficient. Eliminate (B).
Now combine the two statements. As seen above, p can be 45. Try this value of p with the two possible values of q. 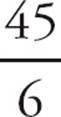 =
= 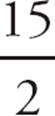 = 7.5 and
= 7.5 and 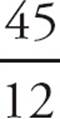 =
= 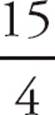 = 3.75. In both cases, the result is a terminating decimal. Try other values of p. Try 15 + 25 + 35 = 75.
= 3.75. In both cases, the result is a terminating decimal. Try other values of p. Try 15 + 25 + 35 = 75. 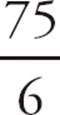 =
= 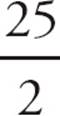 = 12.5 and
= 12.5 and 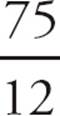 =
= 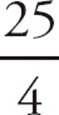 = 6.25. In both cases, again, the result is a terminating decimal. Note that any value of p that satisfies Statement (1) is a multiple of 3. When a multiple of 3 is divided by either 6 or 12, the possible values of q, the 3 that is part of the prime factorization of 6 or 12 gets cancelled out. Dividing by either 2 or 4 always results in a terminating decimal. Therefore,
= 6.25. In both cases, again, the result is a terminating decimal. Note that any value of p that satisfies Statement (1) is a multiple of 3. When a multiple of 3 is divided by either 6 or 12, the possible values of q, the 3 that is part of the prime factorization of 6 or 12 gets cancelled out. Dividing by either 2 or 4 always results in a terminating decimal. Therefore, ![]() is always a terminating decimal, and the two statements combined are sufficient. The correct answer is (C).
is always a terminating decimal, and the two statements combined are sufficient. The correct answer is (C).