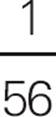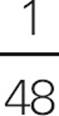Math Workout for the GMAT

Part III Content and Strategy Review

Chapter 2 Number Properties

Many of the questions in the GMAT Math section use a lot of math vocabulary. You probably learned most of these terms in junior high and high school. However, if you’re like most GMAT takers, you haven’t used them in years, so your memory of them is pretty hazy.

This chapter reviews the terms that are most common on the GMAT. We’ll look at the definitions and, more importantly, the way those words are used in GMAT questions. Even if you feel comfortable with the definitions, you should work some or all of the examples to be certain you know how to apply those definitions.

NUMBERS

It’s often helpful to use a number line to describe different types of numbers and their properties. Here’s an example of a number line.

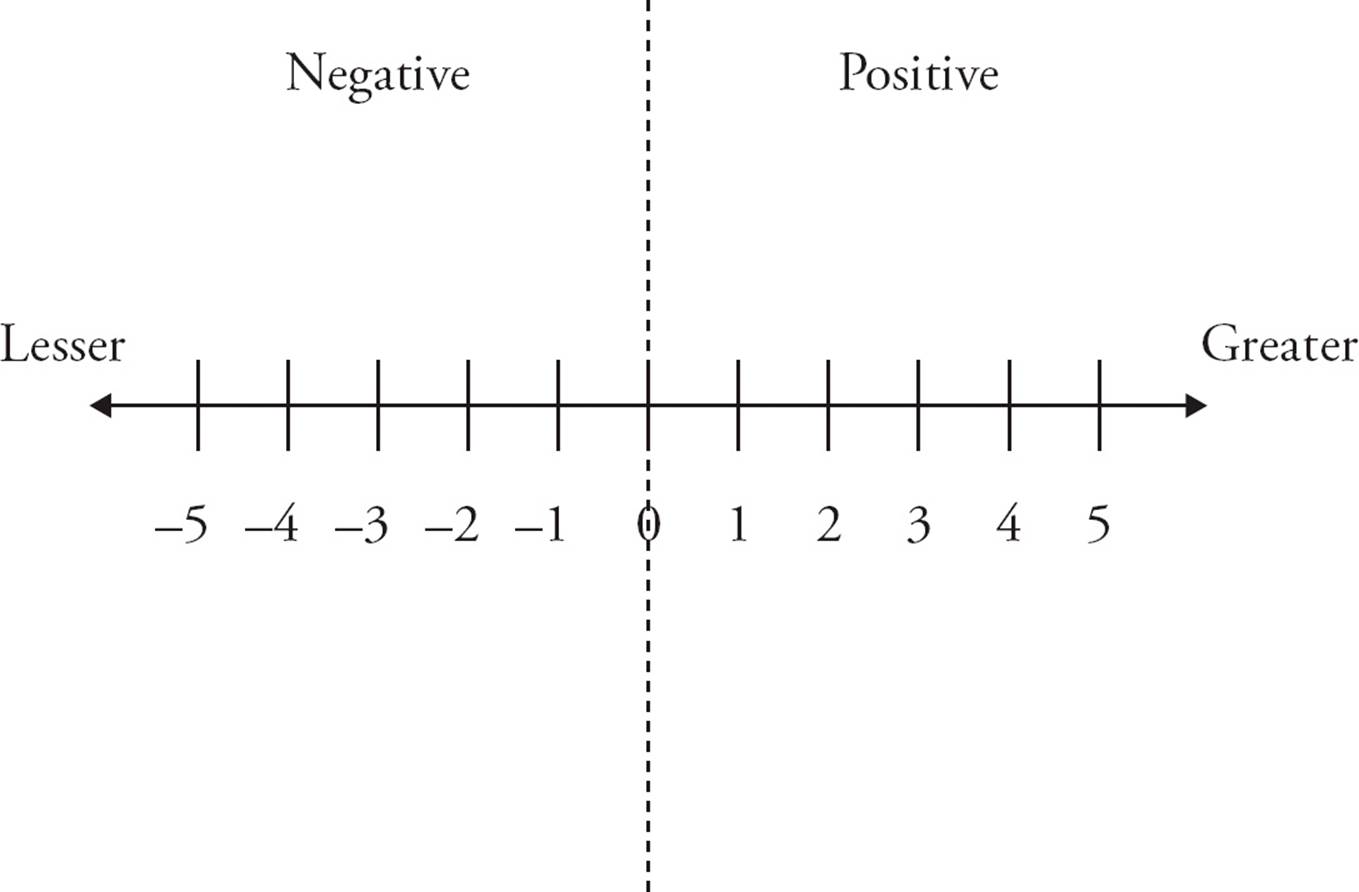
Greater means “to the right” on the number line, while less means “to the left.” So 7 is greater than 5 and 2 is less than 3. Most people find that pretty intuitive. However, it’s easy to get mixed up when you deal with negative numbers. For example, −5 is actually less than −3 even though 5 looks bigger than 3. You can avoid this mistake if you think in terms of “right” and “left” rather than “bigger” and “smaller.”

Positive numbers are greater than zero. Negative numbers are less than zero.

Zero itself is neither positive nor negative. It is usually referred to as neutral.

There are some rules for multiplying (and dividing) positive and negative numbers.

The absolute value of a number refers to that number’s distance from zero. The symbol for absolute value is a pair of vertical lines; so for example, the absolute value of 7 is written as |7|. The easiest way to deal with it is simply to omit the negative sign if the number is negative. For example, |−4|=4. For positive numbers, the absolute value is the same as the number itself. For example, |3|=3.

Distinct numbers are numbers that are not equal. For example, 2 and 3 are distinct numbers, but 4 and 2² are not distinct.

DRILL 1

Answers can be found on this page.

1.Which of the following numbers has the greatest value?

Remember!

For Data Sufficiency
problems in this book, we
do not supply the answer
choices. The five possible
answer choices are the
same every time.

2.What is the value of x ?

(1) |x| = 7

(2) When x is divided by a negative number, the result is negative.

Integers

An integer is what you commonly think of as a positive or negative “counting number.” All of the numbers marked on the number line are integers. The numbers between the marks are not integers. More formally, integers include all positive whole numbers, all negative whole numbers, and 0. For example, numbers such as 1, 2, 3, 0, −1, and −2 are all integers. Numbers such as , 0.072, −, and 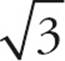are not integers.

Even integers are divisible by 2 with no remainder. Odd integers are not divisible by 2. It’s important to realize that the terms “even” and “odd” apply only to integers. Note that zero is an even integer. There are some rules for multiplying (but not dividing) even and odd integers. If you forget these rules, you can recreate them by trying out some simple numbers.

There are also some rules for adding and subtracting odd and even integers.

Consecutive integers are integers listed in order of increasing value without any integers in between. For example, 1, 2, 3,… is a series of consecutive integers. The GMAT may also ask questions about consecutive even integers, such as 2, 4, 6, 8,…, or consecutive multiples of 7, such as 7, 14, 21, 28,….

The test writers sometimes set traps based upon the terms in the question, hoping that you’re not paying close attention to these important words. Suppose a problem states that “x is a number greater than 0.” If you consider only integers, such as 1 or 5, as possible values for x, you may miss something important. Non-integers have unusual properties in some circumstances. For example, squaring typical integers, such as 2 or 3, results in a larger number. However, squaring the non-integer results in a smaller number. These subtle terminology traps are especially prevalent in data sufficiency questions.

DRILL 2

Answers can be found on this page.

1.If m and n are negative integers, which of the following must be true?

 I.m + n < 0

 II.mn > 0

 III.mn > n

2.If both v and w are odd integers, which of the following could be an even integer?

3.If a, b, and c are consecutive integers, which of the following must be an odd integer?

MANIPULATING NUMBERS

A sum is the result obtained from addition, and a difference is the result from subtraction. A product is the result of multiplication, and a quotient is the result of division.

Whenever you see one of these terms in a problem, you know to perform that operation (add, subtract, multiply, divide).

A remainder is the integer left over from division. This is the way you did division in third grade—no decimals or fractions allowed. Just keep dividing until you get down to something smaller than the number you’re dividing by. That something is the remainder.

For example, let’s divide 7 by 2. Set up the long division like this: 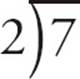. You know that 2 goes into 7 three times (because 2 × 3 = 6).

However, there’s still 1 left over. 1 is smaller than 2, so you can’t continue without getting into decimals. That means 1 is the remainder.

The reciprocal of a number is the number you multiply it by to get 1. In other words, if the product of two numbers, m and n, is 1, then the numbers are reciprocal. If you’re not quite sure what that means, consider some actual numbers. What is the reciprocal of 2? Well, what number can 2 be multiplied by in order to yield a product of 1? 2× = 1. So, the reciprocal of 2 is . If the number you’re starting with is a fraction, the reciprocal can be determined by simply swapping the numerator and denominator in the original fraction. For example, the reciprocal of is .

DRILL 3

Answers can be found on this page.

1.When 12 is divided by the positive integer k, the remainder is k − 3. Which of the following could be the value of k ?

2.If the product xy is negative, which of the following must be true?

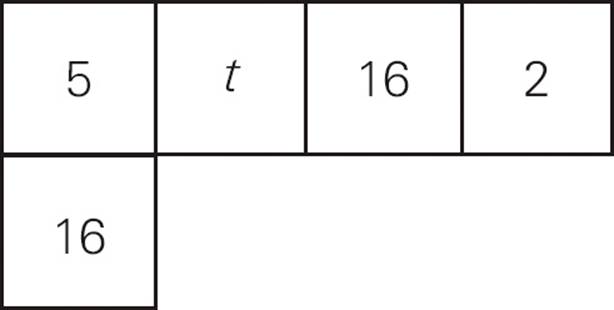
3.In the figure above, the product of the two numbers in the vertical column equals the sum of the four numbers in the horizontal row. What is the value of t ?

ZERO

Zero is a special number because it is unique in a lot of ways. Some of the trickier questions require that you be aware of some of these special characteristics. Zero is an integer, but it is neither positive nor negative. It’s usually referred to as neutral. However, zero does qualify as even.

You can’t divide anything by zero. Division by zero is said to be undefined. Multiplying anything by zero is always zero. Also, zero divided by anything else equals zero.

FACTORS, MULTIPLES, AND DIVISIBILITY

An integer, x, is a factor of another integer, y, if y is divisible by x. In other words, y = nx, where y, n, and x are all integers. For example, 3 × 6 = 18, so 3 and 6 are factors of 18. It’s best to identify factors in pairs. Also, when you’re trying to find all the factors of a number, start with 1 and work your way up. That way you’re less likely to forget a pair.

List all the factors of 24.

1 × 24

2 × 12

3 × 8

4 × 6

When the numbers get close together, like 4 and 6, you know you’ve got them all.

For the quantities x and y, we say that y is a multiple of x if y = nx for some integer n. In other words, to find the multiple of a number, just multiply that number by any integer, for example 1 or 2. The GMAT is generally concerned with only the positive multiples of a number. For example, the multiples of 4 are 4, 8, 12, 16, 20, 24, and so on. Don’t worry about negative numbers or zero, even though they technically can be multiples of a given number. There are an infinite number of multiples for any given number.

If there is no remainder when integer x is divided by integer y, then x is said to be divisible by y. In other words, divisible means you can evenly divide the bigger number by the smaller number. For example, 8 ÷ 2 = 4, so 8 is divisible by 2. However, 10 ÷ 4 = 2.5, so 10 is not divisible by 4.

Here are some shortcuts to help you determine divisibility:

· A number is divisible by 2 if it is an even integer.

· A number is divisible by 3 if the sum of its digits is a number divisible by 3. For example, see whether 108 is divisible by 3. The sum of the digits is 1 + 0 + 8 = 9. Since 9 is divisible by 3, the number 108 is also divisible by 3.

· A number is divisible by 4 if the number formed by its last two digits is divisible by 4. For example, see whether 624 is divisible by 4. The number formed by the last two digits is 24 (just ignore all of the digits except the last two). Since 24 is divisible by 4, the number 624 is also divisible by 4.

· A number is divisible by 5 if it ends in 0 or 5.

· A number is divisible by 6 if it is divisible by both 2 and 3, using the rules above.

· A number is divisible by 9 if the sum of its digits is a number divisible by 9. This is very similar to the “divisible by 3” rule. For example, see whether 902,178 is divisible by 9. The sum of the digits is 9 + 0 + 2 + 1 + 7 + 8 = 27. Since 27 is divisible by 9 (use the rule again if you’re not sure), the number 902,178 is also divisible by 9.

· A number is divisible by 10 if it ends in 0.

Some tougher problems may require you to break a number into its prime factors, which can be thought of as the building blocks of the number. These prime factors play a big role in determining the divisibility of a number and in finding its multiples. You’ll learn more about these concepts later in this chapter.

DRILL 4

Answers can be found on this page.

1.How many multiples of 3 are there between 10 and 90, inclusive?

2.Which of the following is the least positive integer that is divisible by each of the integers from 2 through 5, inclusive?

3.How many of the factors of 42 are divisible by 3 ?

PRIME NUMBERS

A prime number is a number that has exactly two distinct factors, 1 and itself. This means that the number isn’t divisible by anything besides itself and the number 1. The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.

Another thing to note is that 2 is the only even prime number. That’s because all other even numbers are divisible by 2.

If an integer x is a factor of integer y, then x is called a prime factor of y. For example, the prime factors of 6 are 2 and 3 because 2 × 3 = 6. The prime factors of 24 are 2, 2, 2, and 3 because 2 × 2 × 2 × 3 = 24. You could also write this as 2³ × 3 = 24, which is sometimes called the prime factorization of 24. However, if the question asked for the distinct prime factors of 24, they are 2 and 3. You wouldn’t count the extra 2s, because distinct means “not the same.”

An easy way to find the prime factors of a number is a factor tree: Find two factors of the number. Then, find two factors for each factor that isn’t a prime number. Stop when all you have are prime numbers. The following diagram is of a factor tree for 100:

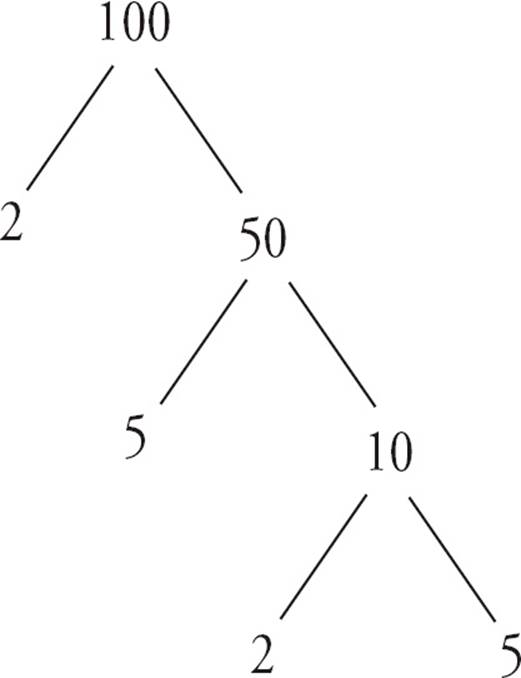
Prime factorization of 100 = 2 × 2 × 5 × 5

Distinct prime factors of 100 are 2 and 5

DRILL 5

Answers can be found on this page.

1.If a and b are distinct prime numbers, which of the following could be the product of a and b ?

2.What is the greatest integer that is a sum of four different prime numbers, each less than 30 ?

3.If x is a prime number greater than 3, what is the remainder when x² is divided by 8 ?

ORDER OF OPERATIONS

There is an order you want to follow when you’re solving a mathematical expression that contains more than one operation. The mnemonic to help you remember the order of operations is P E M D A S. It stands for Parentheses, Exponents, Multiplication, Division, Addition, andSubtraction.

Parentheses are the first step. If you have several operations within a set of parentheses, just apply the order of operations to them. If you have parentheses inside parentheses, start with the innermost ones and work your way out.

Exponents are the next step. Handle all of the exponents before you move on to the other operations. The one exception is if you have operations within an exponent. For example, if you see 3^{2 + 3}, you need to turn that into 3⁵ before you go any further.

Multiplication and division are the next step. They’re really the same thing, so you won’t necessarily do all the multiplication before you do division. Treat them as though they are at the same level and just work from left to right.

Addition and subtraction are the last step. Just as multiplication and division are at the same level, so are addition and subtraction. Just work from left to right.

A Helpful Mnemonic

The sentence Please
Excuse My Dear Aunt
Sally is a helpful
mnemonic tool to
remember the order
of operations.

DRILL 6

Answers can be found on this page.

1.24−12 + 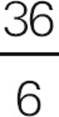−3=

2.(1 + 5) − 3² + 8 ÷ 2 × 2 =

MORE FACTORING

Earlier in this chapter, you learned about the factors of a number and how to break down a number into its prime factorization. It is often useful to think of a number in terms of its factors, which are the building blocks of a number. You will usually be concerned with the prime factors of a number.

For example, take a look at the number 20. Its factors are 1, 2, 4, 5, 10, and 20. Its prime factorization is 2 × 2 × 5, or 2² × 5. Each factor of 20 (except 1), is formed from a subset of the prime factors of 20. The factor 2 uses one of the prime factors 2. The factor 10 incorporates one of the prime factors 2 and the prime factor 5, because 2 × 5 = 10. Once you know the prime factorization of a number, its factors are formed by grouping the prime factors in different ways. Try these concepts in the next problem.

1.Which of the following is NOT divisible by the product of 5, 6, and 8 ?

First, look at the prime factorizations of 5, 6, and 8. 5 is already prime. You can break 6 into 2 × 3 and 8 into 2 × 2 × 2 or 2³. Thus, the product 5 × 6 × 8 can be expressed in prime factorization form: (5)(2 × 3)(2³) = 2⁴ × 3 × 5. Whatever that product is, it includes four factors of 2, one factor of 3, and one factor of 5.

Four of the answers will be divisible by the product. Another way of saying that is the product is a factor of those four answer choices. Each of these four answers must include four factors of 2, one factor of 3, and one factor of 5 (or 2⁴ × 3 × 5). The only answer that doesn’t include at least those factors is (B). It has only three factors of 2, not four. Choose (B).

2.If m and n are integers, and m is a multiple of 5, is mn a multiple of 135 ?

(1) m is a multiple of 3.

(2) n is a multiple of 9.

A multiple of 135 must be a multiple of all of the factors of 135. If you break 135 into its prime factors, you get 135 = 3³ × 5. Thus, mn must include three factors of 3 and one factor of 5 if it is a multiple of 135. You already know that m includes a factor of 5, so you need to look for the factors of 3.

With Statement (1), you learn that m is also a multiple of 3, so it includes at least one factor of 3. However, you need three factors of 3. Without more information, Statement (1) is insufficient. Narrow the possible answers to (B), (C), and (E).

In Statement (2), you learn that n is a multiple of 9, so it must include at least two factors of 3 (because 9 = 3²). Again, you need three factors of 3, so (2) alone is not enough. Eliminate (B).

With both statements together, you have at least one factor of 3 in m and at least two more in n. Combined with the knowledge that m is a multiple of 5, you can determine that mn contains at least the factors 3³ × 5, which makes it a multiple of 135. That answers the question, so (C) is the correct answer.

Factorials

A factorial is closely related to the idea of factors. An exclamation mark after a number, such as 5!, indicates a factorial. The factorial is the product of the indicated numbers and all positive integers less than that number. For example, 5! = 5 × 4 × 3 × 2 × 1. Although you could calculate the value of the factorial (for example, 5! = 120), most factorial problems will be easier if you leave it in factored form. That allows you to cancel like terms and otherwise simplify the numbers. Look at the following example:

3.What is the value of ?

First, write out each factorial in factored form: = 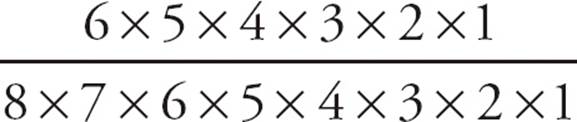. You can cancel the 6, 5, 4, 3, 2, and 1 in the top and the bottom to reduce the fraction to 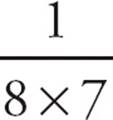= 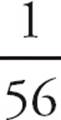. The correct answer is (A).

4.If 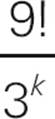is an integer, what is the greatest possible value of k ?

First, write out the factorial in factored form: 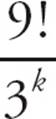= 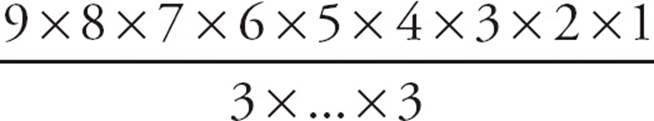. To make the fraction an integer, each of the factors of 3 on the bottom must cancel with a factor of 3 on the top. The 9 on the top has two factors of 3, the 6 has one factor of 3, and the 3 has one factor of 3. That’s four factors of 3 on the top, so the largest that k could be is 4. Four factors of 3 on the bottom would exactly cancel with the four on the top, leaving an integer. The correct answer is (C).

Comprehensive Number Properties Drill

Answers can be found on this page.

Remember!

For Data Sufficiency problems in this book, we do not supply the answer choices. The five possible answer choices are the same every time.

1.If x is a positive integer, then x(x − 1) is

2.Which of the following CANNOT result in an integer?

3.If a + b + c = 36, what is the value of abc ?

(1) a, b, and c are consecutive even integers.

(2) a, b, and c are distinct positive integers.

4.How many positive integers less than 28 are prime numbers, odd multiples of 5, or the sum of a positive multiple of 2 and a positive multiple of 4 ?

5.If a positive integer q is divisible by both 3 and 11, then q must also be divisible by which of the following?

I. 14

II.  33

III. 66

6.If positive integers q and r are both even, which of the following must be odd?

7.What is the value of the two-digit integer n ?

(1) n is divisible by 9.

(2) The tens digit of n is 4.

8.In a decreasing sequence of seven consecutive even integers, the sum of the first four integers is 68. What is the product of the last three integers in the sequence?

9.What is the value of the integer p ?

(1) p is a prime factor of 33.

(2) 3 ≤ p ≤ 15

10.If m is an odd integer and n = 5m + 4, which of the following could be a divisor of n ?

11.(3 + 1)² + (5 − 4 × 2) =

12.If positive integer n is less than or equal to 20, what is the value of n ?

(1) n is divisible by 2 and 5.

(2) n has 2 distinct prime factors.

13.If x is a member of the set {12, 15, 18, 24, 36, 45}, what is the value of x ?

(1) x is divisible by 6.

(2) x is a multiple of 9.

14.What is the value of the sum of a sequence of x consecutive even integers?

(1) x = 5

(2) The least integer in the sequence is 6.

15.If x and z are integers, how many even integers y are there such that x < y < z ?

(1) z – x = 4

(2) x is odd.

16.What is the value of q ?

(1) q =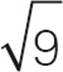

(2) |q| = 3

17.What is the value of the three-digit integer t if t is divisible by 9 ?

(1) The tens digit and the hundreds digit of t are both 7.

(2) The units digit of t is less than both the tens digit and the hundreds digit.

18.If x is a factor of positive integer y, then which of the following must be positive?

19.What is the remainder when n is divided by 3 ?

(1) n is divisible by 5.

(2) n is divisible by 6.

Challenge!

Take a crack at this high-level GMAT question.

20.In a certain game, scoring plays result in 2, 5, or 7 points only. How many times did a team playing this game score 2 points on a play?

(1) The team scored 7 points on a scoring play exactly 3 times.

(2) The product of the point values from all of the team’s scoring plays is 6,860.

ANSWERS AND EXPLANATIONS

Drill 1

1.BThe question asks for the greatest value, so you want the number farthest to the right on a number line. The two absolute values convert to 7.7 and 4.5. Of all five numbers, 7.7 is the greatest, so (B) is the best answer.

2.CStart with Statement (1). You know that x = 7 or −7, but that’s not enough. You can’t answer the question, so narrow down the answers to (B), (C), and (E). Look at Statement (2). From the rules for multiplying and dividing positive and negative numbers, this statement tells you that x is positive, but you don’t have a single value. You can’t answer the question, so eliminate (B). Look at Statements (1) and (2) together. You know that x is positive so the only possible value is 7. Choose (C).

Drill 2

1.EAdding two negative numbers will just result in an even smaller (farther to the left) negative number. So m + n < 0 and I is true. You know that a negative multiplied by a negative results in a positive number. So mn > 0 and II is true. This also means that mn is greater than any negative number, including n. Therefore mn > n and III is true. So the answer is (E).

2.DYou know that an odd integer multiplied by an odd integer results in an odd integer. So vw is odd and you can eliminate (A). An odd integer plus an odd integer results in an even integer. So v + w is even, but v + w + 1 is odd and you eliminate (B). Dividing an odd integer by an odd integer gives you either an odd integer, such as 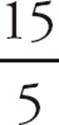= 3, or a non-integer, such as 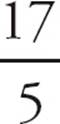= 3. So eliminate (C). An even times an odd is even, so 2v is even. Adding an even to an odd is odd, so 2v + w is odd and you should cross off (E). As we saw earlier, v + w is even, and multiplying by 2 keeps it even. (Even if v + w were odd, multiplying by 2 would make it even.) So (D) is the best answer.

3.EThis is a great problem to approach by Plugging In. Start by setting the values of a, b, and, c equal to 1, 2, and 3, respectively, and then test the answer choices using these numbers. That will eliminate (A), (B), and (D). Next, test (C) and (E) by replacing the values of a, b, and cwith 2, 3, and 4, respectively. (The first round of Plugging In used two odd numbers, and this round will use two even numbers.) When you test (C) and (E) with these new numbers, (E) is the only one that works: 2 × 3 × 4 − 1 = 23.

Drill 3

1.AFor this question, just try out each answer choice and see what the remainder is. If k = 3 then 12 ÷ 3 = 4 with a remainder of 0. Because k − 3 = 0, answer (A) is correct. In answer (B), the remainder is 0 and k − 3 = 1; eliminate it. In answer (C), the remainder is 0 and k − 3 = 3; cross it off. In answer (D), the remainder is 3 and k − 3 = 6; get rid of it. In answer (E), the remainder is 2 and k − 3 = 7, so that’s not right either.

2.DBecause xy is negative, you know that either x is negative and y is positive or vice versa. However, you don’t know which way it is, so eliminate (A) and (B). The rule tells you that division with a positive and a negative results in a negative. Eliminate (C) and choose (D). You can cross off (E) because x + y could be either positive or negative. For example, 3 + (−5) = −2 but (−3) + 5 = 2. It just depends on the particular numbers you use for x and y.

3.DProduct means multiply, so the product of the numbers in the vertical column is 5 × 16 = 80. The sum of the horizontal numbers needs to equal 80 as well. Sum means add, so the sum is 5 + t + 16 + 2 = 23 + t. If 23 + t = 80, then t = 57. Choose (D).

Drill 4

1.BThe simplest way to solve this problem is to list every multiple of 3 from 10 to 90 and then count them. It sounds tedious but it doesn’t really take as long as you think it will. The multiples of 3 are 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, and 90. You include 90 because the question said inclusive. That’s a total of 27 numbers.

2.BThe correct answer must be divisible by 2, 3, 4, and 5. You may think the easiest way is simply to multiply those numbers together, but that’s a trap. Instead, start with the smallest answer choice and see whether it’s divisible by all of those numbers. If not, try the next smallest answer choice. Use the divisibility shortcuts. 30 is divisible by 2, 3, and 5, but not by 4. Eliminate (A). 60 is divisible by 2, 3, 4, and 5. Choose (B). The trap is answer (C). If you multiply 2 × 3 × 4 × 5 you’ll get 120, which is divisible by all of those numbers, but it’s not the leastnumber divisible by them.

3.CFirst, list all of the factors of 42: 1 × 42, 2 × 21, 3 × 14, and 6 × 7. Of these factors, 42, 21, 3, and 6 are all divisible by 3. That’s 4 numbers, so choose (C).

Drill 5

1.CFor each answer, list all the factor pairs and see if any contain two distinct prime numbers. The factors of 4 are 1 × 4 and 2 × 2. Although 2 is a prime number, you need two distinct prime numbers. Eliminate (A). The factors of 5 are 1 × 5. Remember: 1 is not a prime number. Eliminate (B). The factors of 10 are 1 × 10 and 2 × 5. Since 2 and 5 are both prime numbers, choose (C).

2.BThe question asks for the greatest integer, so add up the four largest prime numbers that are less than 30. The numbers are 29, 23, 19, and 17. Remember that not all odd integers are prime. The sum is 29 + 23 + 19 + 17 = 88. Choose (B).

3.BJust pick a prime number greater than 3, such as 5. Square it and you get 5² = 25. Divide 25 by 8 and you get 3 with a remainder of 1. You can try other prime numbers, but you’ll always get a remainder of 1. Choose (B).

Drill 6

1.DThere are no parentheses or exponents, so start with the division. 36 ÷ 6 = 6. Then, do the addition and subtraction from left to right. 24 − 12 = 12. 12 + 6 = 18. 18 − 3 = 15. Choose (D).

2.DFirst, do the parentheses to get (6) − 3² + 8 ÷ 2 × 2. Then do the exponent to get 6 − 9 + 8 ÷ 2 × 2. Next, do the multiplication and division, left to right, to get 6 − 9 + 8. Last do the addition and subtraction, left to right, to get 5. Choose (D).

Comprehensive Number Properties Drill

1.EYou can eliminate (A) because some, but not all, even numbers for x will result in a number divisible by 5. Same with (B). When x is even, x − 1 is odd. When x is odd, x − 1 is even. From the odd/even rules, you know that the product of an even integer and an odd integer will always be even. So x(x −1) will always be even. Choose (E).

2.CFor this question, you need to check each answer to see if there is some combination of numbers that would result in an integer. In (A), try the product of 4 and 5 divided by the reciprocal of 2; 4 × 5 ÷ = 40, which is an integer. Eliminate (A). In (B), try 14 divided by 7, which is 2; 2 is an integer, so eliminate (B). In (D), try 66 divided by 3. The result is 22, which is an integer. Eliminate (D). In (E), try 3 + 5 divided by 2, which is 4, an integer. Eliminate (E). In (C), one prime number divided by a different prime number will never result in an integer because a prime number is only divisible by 1 and itself. Choose (C).

3.AStart with Statement (1). The three numbers must be 10, 12, and 14, so you could multiply them to find the product. You can answer the question, so the answer must be (A) or (D). Look at Statement (2). This doesn’t help because a, b, and c could be any three integers that add up to 36. They could be 10, 12, and 14, but they could also be 1, 2, and 33 or many other combinations. You can’t answer the question, so choose (A).

4.DJust list all the numbers and circle the ones that meet one or more of the criteria. The prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, and 23. The odd multiples of 5 are 5, 15, and 25. The numbers that can be expressed as the sum of a positive multiple of 2 and a positive multiple of 4 are all the even numbers over 4. That gives you 22 numbers. Be sure you don’t double count any of them. Choose (D).

5.BNumbers that are divisible by 3 and 11 include 33, 66, 99, 132, and so forth. You can eliminate I and III because not all these numbers are divisible by 14 or 66. All these numbers are divisible by 33, so choose (B).

6.DAn even integer minus another even integer will always give an even result. Eliminate (A). An even integer divided by another even integer could be even, odd, or not an integer. Eliminate (B). You can also eliminate (C) because adding 1 changes odd to even and vice versa. (E) is wrong because this is even times odd, which will give an even result. qr will always be even because even times even is even. So qr − 1 will always be odd. Choose (D).

7.CStart with Statement (1). If n is divisible by 9, then the sum of its digits is a multiple of 9. However, n could be 18, 27, 36, 45, and so forth. You can’t answer the question, so narrow the choices to (B), (C), and (E). Look at Statement (2). By itself, this statement tells you that n is in the 40s, but it could be 40, 41, 42, and so forth. You can’t answer the question, so eliminate (B). Try Statements (1) and (2) together. The only number in the 40s that is divisible by 9 is 45. You can answer the question, so choose (C).

8.BThe first four integers must be 20, 18, 16, and 14. You can find them by dividing 68 by 4 to get 17. Then, try out different groups of consecutive even integers near 17 until you find the ones that fit. The remaining three numbers are 12, 10, and 8. The product is 12 × 10 × 8 = 960. Choose (B).

9.EStart with Statement (1). 33 has two prime factors: 3 and 11, so you can’t answer the question. Narrow the possible answers to (B), (C), and (E). Look at Statement (2). p could be any integer from 3 to 15. You can’t answer the question, so eliminate (B). Look at (1) and (2) together.p could still be either 3 or 11. You can’t answer the question, so choose (E).

10.BAs you’ll see in more detail in Chapter 5, problems like this can also be solved by Plugging In. Since the problem specifies that m is an odd integer, start by plugging in a value for m in order to solve for n; then determine which of the answer choices divides evenly into your value for n. If you chose 1 for your value for m, the equation could be rewritten as n = 5(1) + 4. So, if m = 1, n = 9. The only answer choice that divides evenly into 9 is 3.

11.CUse the order of operations. Start with the parentheses. Within the second parentheses, do the multiplication before you do the subtraction. This all becomes (4)² + (5 − 8) = 16 + (−3) = 13. Choose (C).

12.ELook at Statement (1). n could be 10 or 20. You can’t answer the question, so narrow the choices to (B), (C), and (E). Look at Statement (2). n could be several numbers, including 6 (prime factors 2 and 3), 10 (prime factors 2 and 5), 12 (prime factors 2 and 3), 14 (prime factors 2 and 7), 15 (prime factors 3 and 5), 18 (prime factors 2 and 3), and 20 (prime factors 2 and 5). You can’t answer the question, so eliminate (B). Look at Statements (1) and (2) together. n could be 10 or 20. You can’t answer the question, so choose (E).

13.ELook at Statement (1). There are 4 numbers in the set that are divisible by 6: 12, 18, 24, and 36. You can’t answer the question, so narrow the choices to (B), (C), and (E). Look at Statement (2). There are 3 numbers in the set that are divisible by 9: 18, 36, and 45. You can’t answer the question, so eliminate (B). Look at Statements (1) and (2) together. There are still 2 numbers that are divisible by 6 and 9: 18 and 36. You can’t answer the question, so choose (E).

14.CLook at Statement (1). This tells you how many numbers to add up, but you don’t know which numbers they are. You can’t answer the question, so narrow the choices to (B), (C), and (E). Look at Statement (2). You know that the sequence starts with 6, but you don’t know how many numbers are in the sequence. You can’t answer the question, so eliminate (B). Look at Statements (1) and (2) together. The sequence is 6, 8, 10, 12, and 14. You could easily find the sum, so choose (C).

15.CLook at Statement (1). It tells you that there are 3 integers between x and z. If x is odd, then there are 2 even integers between x and z. If x is even, there is 1 even integer between x and z. You can’t answer the question, so narrow the choices to (B), (C), and (E). Look at Statement (2). This doesn’t help by itself because you don’t know how much greater z is. You can’t answer the question, so eliminate (B). Look at Statements (1) and (2) together. Since x is odd, there are 2 even integers between x and z. You can answer the question, so choose (C).

16.AStart with Statement (1). Since 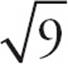= 3, you can find the value of q and answer the question. Narrow your choices to (A) and (D). Look at Statement (2). This only tells you that q = 3 or −3. Don’t let the information you learned in Statement (1) affect your interpretation of Statement (2). You can’t answer the question with the information from Statement (2), so choose (A).

17.AStart with Statement (1). You know from the question that the sum of the digits of t is a multiple of 9. The sum of the tens and hundreds digits is 14. The only possible value for the units digit is 4, which makes t = 774. You can answer the question, so narrow the choices to (A) and (D). Look at Statement (2). This leaves many possibilities for t, including 990, 972, 540, and so forth. You can’t answer the question with Statement (2), so choose (A).

18.EThis problem becomes far more approachable if you use Plugging In. Remember that the largest factor of any integer is the number itself. So, in order to solve this problem, you can start by simply substituting in the same number for x and y. That will immediately eliminate (A), (B), and (D). Next, choose a larger number for y, such as 10, and make x a smaller factor, like 2. Use those values to test (C) and (E); the only answer that works is (E). (Note: You’ll learn more about Plugging In in Chapter 5.)

19.BStart with Statement (1). n could be many different numbers, such as 5, 10, 15, and so forth. leaves a remainder of 2. 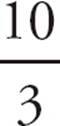leaves a remainder of 1. 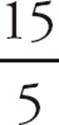leaves a remainder of 0. You can’t pin it down to one value, so you can’t answer the question. Narrow the choices to (B), (C), and (E). Look at Statement (2). Any number that’s divisible by 6 is also going to be divisible by 3. So the remainder will always be 0. You can answer the question, so choose (B).

20.BFirst take a look at Statement (1). Knowing that the team scored 7 points exactly three times does not help you to determine how many times the team scored any of the other point increments. Statement (1) is not sufficient. Your remaining choices are (B), (C), and (E). Now, look at Statement (2). This statement may initially look insufficient, but since the point increments are prime factors, you should first factor 6,860 to get 2 × 2 × 5 × 7 × 7 × 7. Therefore, knowing the product of the points is 6,860, you can determine the number of times 2 points were scored. Choose (B).