Basic Math and Pre-Algebra

PART 1. The World of Numbers

CHAPTER 6. Decimals

Not every number system in history had a way to represent parts of a whole but our system does. In fact, it has two. You’ve already met common fractions, the ones that are written as a quotient of two integers. In this chapter, you’ll get to know decimal fractions.

A decimal fraction, or as most people call it, a decimal, is a representation of part of a whole written in a way that fits into our decimal place value system. In this chapter, you’ll see how to extend the place value system to include parts of a whole, and how to write very small numbers in scientific notation. You’ll look at each of the operations of arithmetic when decimals are involved, and you’ll see that one of the advantages of decimals is that they fit nicely into the methods you already know. Just in case you need to switch between the two ways of writing fractions, you’ll learn to convert from common fractions to decimal fractions and back.

Decimal Fractions

By now you’re familiar with the fractions that are called common, the ones written as a quotient. Now it’s time for a look at decimal fractions. They’re fractions that only use denominators that will fit into the decimal, or base ten, system. Decimal fractions have denominators of 10, or 100, or 1000 and so on, but you hear the denominator in the name rather than seeing it under a fraction bar. The common fraction 3/10 has a numerator of three and a denominator of 10, so you read it as “three tenths.” When that same number is written as a decimal fraction, it’s 0.3. It’s still read “three tenths,” because the 3 is in the tenths place.

The places that follow the decimal point of a number are assigned to be tenths, hundredths, thousandths, and so on, so that the place value tells the denominator. 0.1 is 1 tenth, and 0.01 is 1 hundredth. What would have been the numerator of the fraction becomes the digit in the place that corresponds to its denominator. 0.7 is 7 tenths, the equivalent of 7/10, 0.008 is 8 thousands, or 8/1000, and 0.91 is 91 hundredths, or 91/100. When you write a fraction in the decimal system, the denominator seems to disappear, but you hear it if you give the decimal its proper name.

MATH TRAP

While many people will say “point-3-7-5” for 0.375, its real name is “three hundred seventy-five thousandths.” The “three hundred seventy-five” is the numerator and the “thousandths” names the denominator.

Place a dot, called a decimal point, to the right of the ones digit of a number. This is the divider between the whole and the parts. You’ve probably seen this idea used to write dollars and cents. Three dollars and 12 cents might be written $3.12. This says 3 whole dollars (left side of the decimal point) and 12 pennies, part of a dollar (right side of the decimal point).

Numbers Less than One

Our decimal system is able to represent cents as part of a dollar, but also to represent even smaller parts of any whole, again by working with tens. Decimal fractions, as their name says, are still based on tens. On the left side of the decimal point, as you move to the left, away from the decimal point, the value of that place gets bigger.

Specifically, it gets ten times larger. On the right side of the decimal point, each time you move to the right away from the decimal point, the place value will get smaller. With each step, you’ll break the piece into ten smaller pieces.

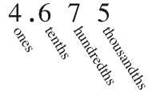
The decimal fractions are written to the right of the decimal point. The first position after the point is the tenths place. It imagines you broke a whole into ten parts, called tenths, and the digit in that place shows how many of those parts you have. In our dollar and cents example, the 1 just to the right of the decimal point is worth one tenth of a dollar, or in other words, a dime.

How many tenths can you have? You might not have any, in which case you could put a zero in that place. If you had 1, or 2, or 3, or 4, or 5, or 6, or 7, or 8, or 9, that digit goes in the tenths place. What if you have more than that? Ten tenths make 1 whole, so make groups of ten tenths, see how many groups you have and put that number in the ones place. The leftovers, if any, will have to be fewer than 10 tenths, so that digit goes in the tenths place. If you had 23 tenths, you’d have 2 groups of 10 tenths and 3 tenths left over, so that would be 2 ones and 3 tenths, or 2.3.

Of course, you might want to break the whole into smaller parts, so the next place to the right imagines you break the whole into 100 parts, each called one hundredth. You can think of it as breaking each tenth into ten parts, or breaking one whole into a hundred parts. You get the same thing.

The digit in the hundredths place tells you how many of those little pieces you have. The number 4.05 says you have 4 ones and 5 hundredths.

WORLDLY WISDOM

Notice that all the places to the right of the decimal have a “th” at the end of their names. That's the signal that you're talking about a fraction.

Do you have more than 9 of these hundredths? A group of 10 hundredths makes one tenth, so count up how many groups you have and that goes in the tenths place, and what’s left over goes in the hundredths place. You can think of the number 0.48 as 48 hundredths, or as 4 tenths and 8 hundredths.

If you had more than a hundred hundredths, you’d make a 1 from each group of 100. When you’ve made all the groups of 100 you can, you can look for groups of 10 hundredths to make tenths, and the leftovers would go in the hundredths place. If you had 793 hundredths, you’d have 7 groups of 100 hundredths, 9 groups of 10 hundredths, and 3 hundredths left over. That’s 7 ones, 9 tenths and 3 hundredths, or 7.93, seven and ninety-three hundredths.

Different Names, Same Number

Decimal fractions can sometimes go by more than one name. If you write 3.82, you read that as “three and eighty-two hundredths.” You have three wholes and eighty-two of the fractions that are created by breaking one into 100 parts. Those eighty-two hundreds can make 8 groups of ten hundredths or eight tenths, with two hundredths left over, so there’s an 8 in the tenths place and a 2 in the hundredths place.

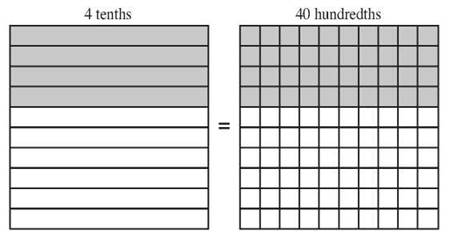
Now suppose you write 3.820, which you’d read as “three and eight hundred twenty thousandths.” You read this number differently because it fills in the thousandths place, but its value is exactly the same as 3.82. All you added was zero thousandths—nothing!

Trailing zeros at the end of a decimal fraction change the way you read the name of the number, but they don’t change the value of the number. The numbers 1.7, 1.70, and 1.700 all have the same value. They would be read as “one and seven tenths,” “one and seventy hundredths,” and “one and seven hundred-thousandths,” but they’re all worth the same amount. If you wrote them as common fractions, 1.7 would be , 1.70 would be  which reduces to , and 1.7000 would be  which also reduces to . As a result, you’ll often want to drop any trailing zeros to make the look of the number simpler.

CHECK POINT

1. Write the number 9.003 in words.

2. Write the number 82.4109 in words.

3. Write the number “forty-two hundredths” in numerals.

4. Write the number “forty-two ten-thousandths” in numerals.

5. Write the number “three hundred twelve and nine hundred one thousandths” in numerals.