Numbers: Their Tales, Types, and Treasures.
Chapter 6: Number Explorations
6.5.THE BINOMIAL EXPANSION
The Pascal triangle contains many unexpected number relationships beyond the characteristics that Pascal intended in his original use of the triangle. Pascal's original use was to exhibit the coefficients of successive terms of a binomial expansion.
We shall now consider the binomial expansion—that is, taking a binomial such as (a + b) to successively higher powers. By now, you ought to be able to recognize the pattern formed by the coefficients of the terms shown in figure 6.9. The coefficients of each of the binomial-expansion lines is also represented as a row of the Pascal triangle.
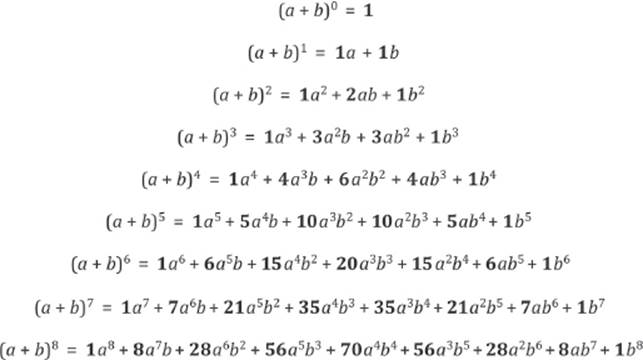
Figure 6.9: The binomial expansion.
This allows us to expand a binomial without actually multiplying it by itself many times to get the end result. There is a pattern also among the variables’ exponents: one descends while the other ascends in value—each time keeping the sum of the exponents constant—that is, the sum is equal to the exponent of the power to which the original binomial was taken.
The formulas in figure 6.9 can be written in compact form in a single line, which we provide here because of its beauty. This formula is called the binomial theorem.
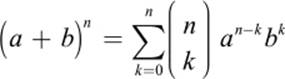
The symbol ![]() is pronounced “n over k.” This is the modern notation for the numbers in the Pascal triangle, the so-called binomial coefficients, which we denoted by B(n,k) in chapter 5.
is pronounced “n over k.” This is the modern notation for the numbers in the Pascal triangle, the so-called binomial coefficients, which we denoted by B(n,k) in chapter 5.
Actually, there is a formula that allows us to compute any binomial coefficient given its position n,k in the Pascal triangle, without having to evaluate the binomial coefficients above. This formula uses the notation
n! = 1 × 2 × 3 ×…× (n – 1) × n
for the product of all natural numbers from 1 to n. The expression n! is pronounced “n-factorial.” With this abbreviation, the binomial coefficient is given by
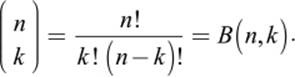
For example,
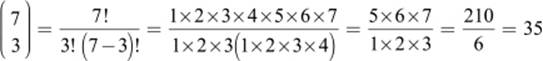
gives the binomial coefficient B(7,3) = 35. According to chapter 5, it describes in how many ways we can choose three elements out of a set of seven elements. It also tells us how many ways seven coin tosses come up with three heads.
For a = 1 and b = 1, the expressions in figure 6.9 can be simplified, as all products of powers of a and b can be replaced by 1. We obtain, for example,
(1 + 1)6 = 26 = 1 + 6 + 15 + 20 + 15 + 6 + 1,
which is just the sum of the entries in the corresponding row of the Pascal triangle. In that way, we can reproduce the result of figure 5.12: The sums across the lines of the Pascal triangle are the powers of 2.
For a = 10 and b = 1, all factors an bk in figure 6.9 simply become 10n. This leads to an interesting observation. For example,
(10 + 1)3 = 113 = 1 × 103 + 3 × 102 + 3 × 101 + 1 = 1,331.
The binomial formula, in this case, provides the representation of a number in our decimal numeral system. And the digits of this number are the entries of the Pascal triangle in the corresponding row. This shows us that if one reads a row of the Pascal triangle as a single number whose digits are the elements of that row, we get a power of 11. Indeed, 121 = 112, and the numbers 1, 4, 6, 4, 1 in the fourth row lead to 14,641 = 114. However, beginning with the fifth row, we would have to regroup the digits:
115 = 1 × 105 + 5 × 104 + 10 × 103 + 10 × 102 + 5 × 101 + 1 = 161,051.
In this case, some of the elements in the Pascal triangle have more than one digit, and one has to carry the leading digits over to the next order. So, for example, the sixth power of 11 has to be computed as follows:
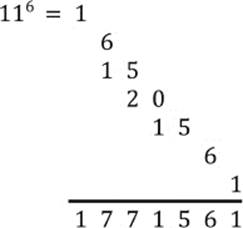
Figure 6.10: How to determine a power of 11 from the Pascal triangle.
The occurrence of Fibonacci numbers, powers of 2, and powers of 11 in the Pascal triangle are once again illustrated in figure 6.11.
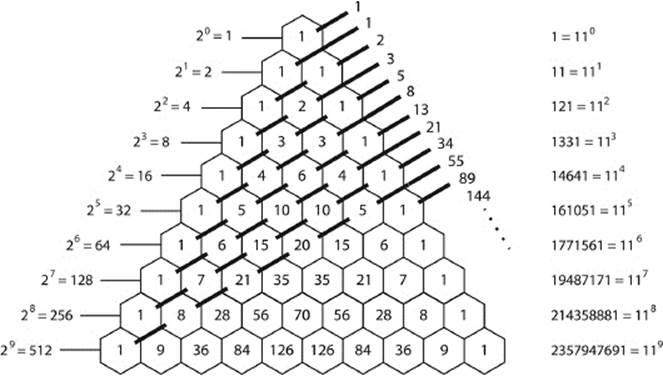
Figure 6.11: Amazing number relationships in the Pascal triangle
There are many number relationships present in the Pascal triangle. The turf is fertile. The opportunity to find more gems in this triangular arrangement of numbers is practically boundless! We encourage the motivated reader to search for more hidden treasures embedded in this number arrangement.