Numbers: Their Tales, Types, and Treasures.

Chapter 7: Placement of Numbers

7.4.CONSTRUCTION OF A MAGIC SQUARE OF ORDER 3

A systematic construction of all possible 3 × 3 magic squares would begin by considering the matrix of letters representing the numbers 1 to 9 shown in figure 7.9. Here the sums of the rows, columns, and diagonals are denoted by r_j, c_j, and d_j, respectively. In a magic square of order 3, all these number sums would be equal to the magic number 15.

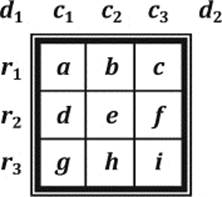
Figure 7.9: A map of a general magic square

In a magic square, we would thus have

r₂ + c₂ + d₁ + d₂ = 15 + 15 + 15 + 15 = 60.

However, this sum can also be written as

r₂ + c₂ + d₁ + d₂ = (d + e + f) + (b + e + h) + (a + e + i) + (c + e + g) =
3 e + (a + b + c + d + e + f + g + h + i) = 3e + 45

Therefore, 3e + 45 = 60, and e = 5. Thus it is established that the center position of a magic square of order 3 must be occupied by the number 5.

Recall that two numbers of an nth order magic square are said to be complementary if their sum is n² + 1. In a 3 × 3 magic square, two numbers are complementary if their sum is 9 + 1 = 10. We can now see that numbers on opposite sides of 5 are complementary. For example, a + i = d₁– e = 15 – 5 = 10, and, therefore, a and i are complementary. But so are the pairs g and c, b and h, and d and f.

Let us now try to put 1 in a corner, as shown in figure 7.10. Here a = l, and therefore i must be 9, so that the diagonal adds up to 15. Next we notice that 2, 3, and 4 cannot be in the same row (or column) as 1, since there is no natural number less than 9 that would be large enough to occupy the third position of such a row (or column). This would leave only the two shaded positions in figure 7.10 to accommodate these three numbers (2, 3, and 4). Since this cannot be the case, our first attempt was a failure: the numbers 1 and 9 may occupy only the middle positions of a row (or column).

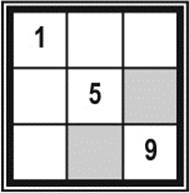
Figure 7.10: A non-magic-square construction—false start.

Therefore, we have to start with one of the four possible, positions remaining for 1, for example, as we show in the first square of figure 7.11. We note that the number 3 cannot be in the same row (or column) as 9, for the third number in such a row (or column) would again have to be 3 to obtain the required sum of 15. This is not possible, because a number can be used only once in the magic square. Additionally, we have seen above that 3 cannot be in the same row (or column) as 1. This leaves only the two shaded positions in figure 7.11 for the number 3. The number opposite 3 is always 7, because then 3 + 5 + 7 = 15.

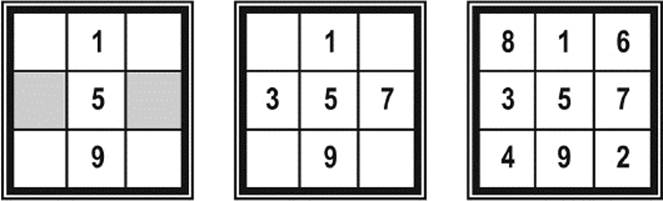
Figure 7.11: The development of one of several possible magic squares.

We continue with the second square in figure 7.11, showing one of two possibilities for the placement of 3 and 7 (the other possibility has 3 and 7 exchanged). It is now easy to fill in the remaining numbers. There is only one such possibility, shown in the third square of figure 7.11.

How many different squares are there? We could start by putting the number 1 in any of the four positions in the middle of a side. We then have two possibilities for placing 3. After that, the construction is unique. This produces the eight magic squares shown in figure 7.12.

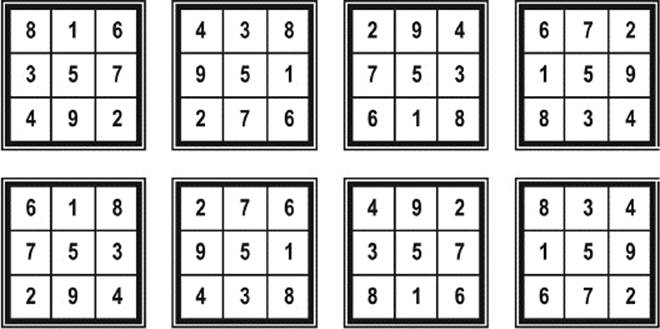
Figure 7.12: There are precisely eight magic squares of order 3.