Numbers: Their Tales, Types, and Treasures.

Chapter 7: Placement of Numbers

7.5.CONSTRUCTING ODD-ORDER MAGIC SQUARES

You might now want to extend this technique to construct other odd-order magic squares. However, it can become somewhat tedious. The following is a rather mechanical method for constructing an odd-order magic square.

Begin by placing a 1 in the first position of the middle column. Continue by placing the next consecutive numbers along the diagonal line, as in figure 7.13.

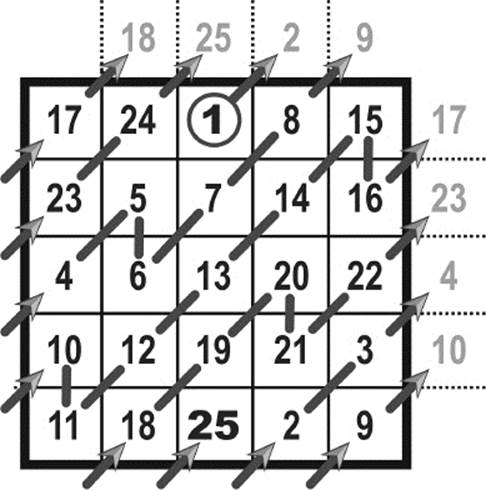
Figure 7.13: Construction of an odd-order magic square.

Whenever you drop off the square on one side, you enter again on the opposite side. So the gray number 2 in figure 7.13 (which fell off the grid) must be placed in the last row. Analogously, the gray number 4 will be placed in the first column. The process continues by consecutively filling each new cell along the diagonal line until an already-occupied cell is reached (as is the case with the number 6). Rather than placing a second number in an already-occupied cell, the number is placed below the previous number. The process continues until the last number is reached. After some practice with this procedure, you will begin to recognize certain patterns (e.g., the last number always occupies the middle position of the bottom row). This is just one of many ways of constructing odd-order magic squares. Not counting rotations and reflections, there are 275,305,224 different 5 × 5 magic squares. Exact numbers for higher-order magic squares are unknown.