Numbers: Their Tales, Types, and Treasures.
Chapter 10: Numbers and Proportions
10.1.COMPARING QUANTITIES
When the mathematicians of ancient Greece spoke about “numbers,” they meant “natural numbers.” Although they knew about fractions from Babylonian and Egyptian science, and could use them in a practical sense, they did not accept fractions as numbers. To them, a fraction was not a number but a certain relationship between two quantities, and it would have been called a proportion rather than a number.
Today, the word proportion occurs mainly in geometry, when we speak of the proportions, or similarity, of geometrical shapes. Indeed, the proportion of the sides of a rectangle is very familiar from everyday life and is often called the “aspect ratio” (or the format) of the rectangle. For example, a modern television screen would have the aspect ratio 16:9 (see figure 10.1), and there are two common proportions of images produced by digital cameras, 3:2 and 4:3.
A rectangle that is 16 inches long and 9 inches wide would be an example of the proportion 16:9, as would be a rectangle 32 inches long and 18 inches wide. The lengths of the sides are not important, but their relation is what matters because this defines the shape of the rectangle. Rectangles with the same proportion have the same shape, even if they are of a different size.

Figure 10.1: The proportion 16:9.
As we said, ancient Greek mathematicians did not describe a proportion a:b, which we today see as a fraction, as a number. They considered only the counting numbers, or natural numbers. Consequently, a proportion of quantities could not be represented by a single number; it had to be considered as a relationship between quantities. The founder of a general theory of proportions was Eudoxus of Cnidus (ca. 395–340 BCE), one of the greatest Greek mathematicians. We know about his work only through the reports of others, and Eudoxus's theory of proportions is contained in Euclid's Elements.
In some cases, a proportion can be expressed through two natural numbers, like the proportion 16:9. In the Pythagorean era, the only theory of proportions that was available was the one between natural numbers. Pythagoreans used this theory to explain the universe. Musical scales may serve as an example, because, according to Archimedes, “they presumed the whole heaven to be a musical scale and a number.”1 The Pythagorean scale is built on simple proportions that can be demonstrated on a monochord, which is a musical instrument that has a single string stretched over a resonance box, as shown in figure 10.2. The string oscillates with a particular frequency, producing the fundamental tone of the instrument. The length of the oscillating part of the string can be adjusted by moving a slider to vary the sound. The Pythagoreans discovered that one would obtain especially pleasing (consonant) musical intervals if the ratio between the whole string and the oscillating part of the string could be expressed in terms of small integers. If the length of the string was halved (by positioning the slider at 6), it would produce, when plucked, a pitch an octave higher, and the frequency would be twice the frequency of the original, realizing a proportion of 2:1. If you divide the string at position 8, as shown in figure 10.2, you would create a proportion of 3:2. This would produce a pitch that is a fifth higher than the fundamental tone. And if you place the slider at 9, the pitch would be a fourth higher than the fundamental tone, corresponding to the proportion 4:3. The whole Pythagorean musical scale is built around these simple proportions of string lengths.
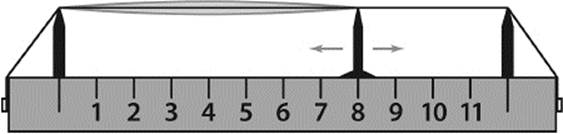
Figure 10.2: The monochord.
Impressed by the explanatory force of proportions, the Pythagoreans believed that one should be able to express any proportion of any two quantities in terms of natural numbers n and m, and they regarded proportions involving small natural numbers as particularly pleasing.